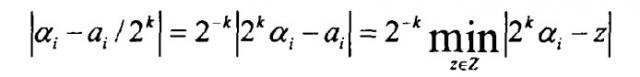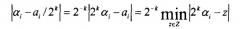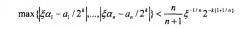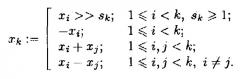Быстрое вычисление произведений посредством двоичных дробей со знакосимметричными ошибками округления

Быстрое вычисление произведений посредством двоичных дробей со знакосимметричными ошибками округления

Иллюстрации

Показать все

Реферат

ОБЛАСТЬ ТЕХНИКИ

Объект изобретения здесь относится, в общем, к обработке и более конкретно к способам аппроксимации, используемым в обработке аппаратным обеспечением и программным обеспечением.

УРОВЕНЬ ТЕХНИКИ

Арифметические сдвиги могут использоваться, чтобы выполнять умножение или деление целых чисел со знаком степени два. Сдвиг влево на n бит над двоичным числом со знаком или без знака имеет эффект умножения его на 2ⁿ. Сдвиг вправо на n бит над дополненным до двойки двоичным числом со знаком имеет эффект деления его на 2ⁿ, но это всегда округляет вниз (т.е. к отрицательной бесконечности). Так как сдвиги вправо не являются линейными операциями, арифметические сдвиги вправо могут добавлять ошибки округления и вырабатывать результаты, которые могут не быть равными результату умножения, за которым следует сдвиг вправо.

В некоторых вариантах реализации, знакосимметричный алгоритм может использоваться в архитектуре преобразования IDCT или другом цифровом фильтре.

Один пример использования арифметических сдвигов находится в вариантах реализации с фиксированной точкой некоторых алгоритмов обработки сигналов, таких как FFT, DCT, MLT, MDCT и т.д. Такие алгоритмы обработки сигналов обычно аппроксимируют иррациональные (алгебраические или трансцендентные) коэффициенты в математических определениях этих алгоритмов с использованием двоичных рациональных дробей. Это обеспечивает возможность выполнения умножений на эти иррациональные дроби с использованием целочисленных добавлений и сдвигов, нежели более сложных операций.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Произведение целочисленного значения и иррационального значения может определяться посредством знакосимметричного алгоритма. Обработка может определять возможные алгоритмы, которые минимизируют метрики, такие как средняя асимметрия, средняя ошибка, дисперсия ошибки и величина ошибки. При заданных целочисленной переменной x и рациональных двоичных константах, которые аппроксимируют иррациональную дробь, может вырабатываться последовательность промежуточных значений, которые являются знакосимметричными. При заданной последовательности операций суммирования, вычитания и сдвига вправо знакосимметричный алгоритм может аппроксимировать произведение целого числа и иррационального значения. Другие операции, такие как суммирования или вычитания 0 или сдвиги на 0 бит, могут быть удалены, чтобы упрощать обработку.

Это изложение предоставлено, чтобы ввести выбор понятий в упрощенной форме, которые дополнительно описываются ниже в подробном описании. Эта сущность не предназначается, чтобы идентифицировать ключевые признаки или существенные признаки заявляемой сущности, и также она не предназначается для использования, чтобы ограничивать объем заявляемого объекта изобретения.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Фиг.1 является графиком результатов различных вычислительных алгоритмов.

Фиг.2 является диаграммой последовательности операций иллюстративной обработки определения знакосимметричного алгоритма, чтобы определять произведение.

Фиг.3 - это иллюстративная архитектура, реализующая алгоритм IDCT с фиксированной точкой.

Фиг.4 - это блок-схема иллюстративной кодирующей системы.

Фиг.5 - это блок-схема иллюстративной системы декодирования.

ПОДРОБНОЕ ОПИСАНИЕ

Дискретные косинусные преобразования (DCT) и обратные дискретные косинусные преобразования (IDCT) выполняют операции умножения с иррациональными константами (т.е. косинусами). В варианте осуществления вариантов реализации DCT/IDCT, аппроксимации вычисляемых произведений этих иррациональных констант могут выполняться с использованием арифметики с фиксированной точкой. Один способ для преобразования значений с плавающей точкой в значения с фиксированной точкой основывается на аппроксимациях иррациональных коэффициентов α_i посредством двоичных дробей:

αi ≈ ai/2k

(1)

где как a_i, так и k являются целыми числами. Умножение x на коэффициент α_i обеспечивает вариант реализации аппроксимации в целочисленной арифметике следующим образом:

xαi ≈ (x*ai)>>k

(2)

где >> обозначает побитную операцию сдвига вправо.

Число битов точности, k, может оказывать влияние на сложность двоичных рациональных аппроксимаций. В программных вариантах реализации параметр точности k может ограничиваться разрядностью регистров (например, 16 или 32) и последствие неудовлетворения такого ограничения варианта осуществления может давать результатом увеличение времени исполнения для преобразования. В аппаратных вариантах осуществления параметр точности k оказывает влияние на количество логических элементов, необходимых, чтобы реализовывать блоки суммирования и блоки перемножения. Следовательно, цель в вариантах осуществления с фиксированной точкой - это минимизировать полное количество битов k, при сохранении достаточной точности аппроксимаций.

Без каких-либо конкретных ограничений на значения для α_i, и предполагая, что для любого данного k, соответствующие значения переменных a_i могут выбираться так, что

и абсолютная ошибка аппроксимаций в (1) должна быть обратно пропорциональной 2^k:

То есть, каждый дополнительный бит точности (т.е. увеличение k) должен уменьшать ошибку наполовину.

В некоторых вариантах реализации частота ошибок может улучшаться, если значения α₁, αn, подлежащие аппроксимации, могут масштабироваться посредством некоторого дополнительного параметра ξ. Если α₁,..., α_n являются набором n иррациональных чисел (n≥2), то существует бесконечно много n+2-кортежей a₁,..., a_n, k, ξ, с a₁,..., a_n ∈ Z, k ∈ N, и ξ ∈ Q, так что

Другими словами, если алгоритм может изменяться так, что все из его иррациональных коэффициентов α₁,..., α_n могут предварительно масштабироваться посредством некоторого параметра ξ, то должны быть аппроксимации, имеющие абсолютную ошибку, которая уменьшается так быстро как 2-k(1+1/n). Например, когда n=2, может иметься приблизительно 50% более высокая эффективность в использовании битов. Для больших наборов коэффициентов α₁,..., α_n, однако, это усиление может быть более маленьким.

Двоичные аппроксимации, показанные в отношениях (1, 2) выше, сводят проблему вычисления произведений на иррациональные константы к умножениям на целые числа. Умножение целого числа на иррациональный коэффициент , с использованием его 5-битной двоичной аппроксимации 23/32, иллюстрирует процесс аппроксимации иррациональных констант. Рассматривая двоичный битовый шаблон 23=10111 и заменяя каждую "1" на операцию суммирования, произведение целого числа при умножении на 23 может определяться следующим образом:

x*23=(x<<4)+(x<<2)+(x<<1)+x

Эта аппроксимация требует 3 операции суммирования и 3 операции сдвига. Дополнительно отмечая, что последние 3 цифры формируют последовательность из "1", может использоваться следующее:

x*23=(x<<4)+(x<<3)-x,

что уменьшает сложность до только 2 операций сдвига и 2 операций суммирования.

Последовательности операций "+", ассоциированные с изолированными цифрами "1", или "+" и "-", ассоциированные с началами и концами серий "1...1", обычно указываются как разложение "канонических цифр со знаком" (CSD). CSD является хорошо известным вариантом реализации в варианте осуществления схем с меньшим количеством множителей. Однако разложения CSD не всегда вырабатывают результаты с наименьшими количествами операций. Например, рассматривая 8-битную аппроксимацию такого же коэффициента 1/≈181/256=10110101 и его разложение CSD:

x*181=(x<<7)+(x<<5)+(x<<4)+(x<<2)+x,

которое использует 4 операции суммирования и 4 операции сдвига. Посредством перестановки вычислений и повторного использования промежуточных результатов может конструироваться более эффективный алгоритм:

x2=x+(x<<2);	//	101
x3=x2+(x<<4);	//	10100
x4=x3+(x2<<5);	//	10110101	=x*181

В соответствии с вариантом реализации вычисление произведений на двоичные дроби может быть получено посредством обеспечения возможности использования сдвигов вправо как элементарных операций. Например, рассматривая коэффициент 1/≈23/32=10111 и используя операции сдвига вправо и операции суммирования согласно его разложению CSD, получается следующее:

x*23/32~(x>>1)+(x>>2)-(x>>5)

(3)

или дополнительно отмечая, что 1/2+1/4=1-1/4:

x*23/32~x-(x>>2)-(x>>5)

(4)

Другим способом вычисления произведения на тот же коэффициент является

x*23/32~x-((x+(x>>4))>>2)+((-x)>>6)

(5)

Фиг.1 иллюстрирует графики значений, выработанных алгоритмами (3, 4 и 5) по отношению к умножению целого числа и иррациональной дроби 23/32. Каждый алгоритм (3, 4 и 5) вычисляет значения, которые аппроксимируют произведения при умножении на иррациональную дробь 23/32; однако ошибки в каждой из этих аппроксимаций являются разными. Например, алгоритм (4) вырабатывает все положительные ошибки с максимальной величиной 55/32. Алгоритм (3) имеет более уравновешенные ошибки с величиной колебаний в пределах ±65/64. Наконец, алгоритм (5) вырабатывает вполне знакосимметричные ошибки с колебаниями в ±7/8. Таким образом, знакосимметричный алгоритм будет вырабатывать уравновешенные (сбалансированные) результаты, которые минимизируют ошибки.

Свойство знаковой симметрии алгоритма (x)⇝xa_i/2^b означает, что для любого (x ∈ Z):

(-x)=-(x)

и это также влечет, что для любого N, и предполагая, что (0)=0:

то есть ошибка с нулевым средним на любом симметричном интервале.

Это свойство может использоваться в варианте осуществления алгоритмов обработки сигналов, так как оно минимизирует вероятность того, что ошибки округления, введенные аппроксимациями с фиксированной точкой, будут накапливаться. Описанное ниже является основой для базирующихся на сдвиге вправо знакосимметричных алгоритмов для вычисления произведений на двоичные дроби, а также верхних границ для их сложности.

При заданном наборе двоичных дробей a₁/2^b,..., a_m/2^b может быть задан алгоритм

A_ai,...,a_m,b(x)⇝(xa₁/2^b,..., xa_m/2^b)

как следующая последовательность этапов:

x₁, x₂,..., x_t,

где x₁:= x и где последующие значения x_k (k=2,...,t) вырабатываются посредством использования одной из следующих элементарных операций:

Алгоритм оканчивается, когда существуют индексы j₁,..., j_m≤t, такие, что

x_j1~x*a₁/2^b,..., x_jm~x*a_m/2^b

Таким образом, некоторые варианты реализации рассматривают алгоритмы, которые минимизируют одну или более из следующих метрик:

средняя асимметрия:

средняя ошибка:

дисперсия ошибки:

величина ошибки:

При вычислении произведений на множественные константы ,..., могут использоваться значения наихудшего случая вышеописанных метрик (вычисленных для каждой из констант ,..., ), чтобы оценивать эффективность алгоритма.

Фиг.2 показывает этапы в процессе 100 для вычисления произведения. На этапе 102 принимается целочисленное значение, и на этапе 104 устанавливаются рациональные двоичные константы, представляющие иррациональное значение, подлежащее умножению на целое число. На этапе 106 могут определяться промежуточные значения. Например, при заданной целочисленной переменной x и наборе рациональных двоичных констант ,..., последовательность промежуточных значений может определяться следующим образом:

w₀, w₁, w₂,..., w_t

где w₀=0, w₁=x, и для всех k≥2 значения w_k получаются следующим образом:

w_k= ± w_i ± (w_j>>s_k) (i, j<k),

где знаки ± влекут операцию либо плюс или минус, которая должна выполняться с обоими членами, и >> обозначает сдвиг вправо переменной z_j на s_k бит.

На этапе 108 определяются точки в этой последовательности, соответствующей произведениям. То есть, результат этого этапа - это индексы l₁,..., l_m ≤ t, так что

На этапе 110 результирующие выходные значения анализируются по отношению к некоторым метрикам точности. Например, эти значения могут анализироваться, чтобы определять, минимизируют ли они один параметр из: среднее, асимметрия, дисперсия, амплитуда.

В некоторых вариантах реализации, процесс 100 может удалять суммирования, или вычитания 0, или сдвиги на 0 бит. В некоторых вариантах реализации, последовательность промежуточных значений может выбираться так, что полная вычислительная (или реализационная) стоимость этой всей операции является минимальной.

Таким образом, при заданном наборе метрик могут иметься алгоритмы, имеющие сложность, которая может характеризоваться полным количеством суммирований, полным количеством сдвигов и т.д. Как таковой, имеется алгоритм, который имеет наименьшее количество суммирований, наименьшее количество сдвигов, наименьшее количество суммирований и сдвигов и наименьшее количество суммирований среди алгоритмов, достигающих наименьшее количество суммирований и сдвигов и т.д.

Фиг.3 иллюстрирует показанную в качестве примера архитектуру 120 IDCT 8×8 с фиксированной точкой. Архитектура может реализовывать алгоритмы, которые являются знакосимметричными значениями x. Во многих вариантах реализации, такие алгоритмы могут быть наименее сложными для заданного набора коэффициентов. Как отмечалось выше, вариант осуществления преобразований IDCT может быть симметричным или давать результатом хорошо уравновешенные ошибки округления. В некоторых вариантах реализации, могут анализироваться оценки метрик, таких как среднее, дисперсия и величина (максимальные значения) ошибок, вырабатываемых алгоритмами. При оценке сложности алгоритмов в расчет могут браться количества операций, также как самый длинный путь исполнения, и максимальное количество промежуточных регистров, требуемых для вычислений.

В некоторых вариантах реализации, архитектура, используемая в варианте осуществления предложенной архитектуры 120 IDCT с фиксированной точкой, может характеризоваться наличием разделимых и масштабируемых признаков. Этап 122 масштабирования может включать в себя одиночную матрицу 8×8, которая предварительно вычисляется посредством разложения на множители 1D коэффициентов масштабирования, для строкового преобразования с 1D коэффициентами масштабирования для столбцового преобразования. Этап 122 масштабирования может также использоваться, чтобы предварительно назначать P бит точности каждому из входных коэффициентов DCT, тем самым обеспечивая "мантиссу" фиксированной точки для использования всюду в оставшейся части преобразования.

В одном варианте реализации, основа для варианта осуществления масштабированного 1D преобразования может быть вариантом хорошо известной факторизации C. Loeffler, A. Ligtenberg и G.S. Moschytz с 3 плоскостными вращениями и 2 независимыми коэффициентами γ=√2. Чтобы обеспечивать эффективные рациональные аппроксимации констант α, β, δ, ε, η и θ в факторизации LLM, два плавающих коэффициента ξ и ζ могут использоваться и применяться к двум подгруппам этих констант следующим образом:

Эти умножения могут инвертироваться посредством ξ и ζ на этапе 122 масштабирования посредством умножения каждого входного коэффициента DCT с соответствующим обратным ξ и ζ. То есть, вектор коэффициентов масштабирования может вычисляться для использования на этапе 122 масштабирования до первого в каскаде 1D преобразований (например, этапы 126 и 128):

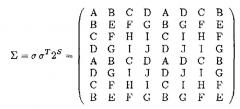
Эти коэффициенты могут впоследствии объединяться в масштабирующую матрицу, которая предварительно вычисляется следующим образом:

где A-J обозначают уникальные значения в этом произведении:

и S обозначает количество битов точности фиксированной точки, назначенных для масштабирования.

Этот параметр S может выбираться так, что он является большим чем или равным количеству битов P для мантиссы каждого входного коэффициента. Это обеспечивает возможность масштабирования коэффициентов F_vu для реализации следующим образом:

F′_vu=(F_vu*S_vu)>>(S-P)

где S_vu≈Σvu обозначают целочисленные аппроксимации значений в матрице коэффициентов масштабирования.

В конце последнего этапа преобразования в последовательности 1D преобразований (этапы 126 и 128) P бит мантиссы фиксированной точки (плюс 3 дополнительных бита, накопленные в течение исполнений каждого из 1D этапов) просто сдвигаются вне выходных результатов преобразования посредством операций 130 сдвига вправо следующим образом:

Чтобы гарантировать должное округление вычисленного значения, смещение 2P+2 может добавляться к значениям f′_yx до сдвигов с использованием этапа 124 смещения DC. Это округляющее смещение реализуется посредством возбуждения коэффициента DC до исполнения первого 1D преобразования:

F′′₀₀=F′₀₀+2^P+2

В некоторых вариантах реализации, уравновешенные (т.е. знакосимметричные) алгоритмы, как описано выше, могут использоваться в стандарте IDCT ISO/IEC 23002-2. Этот стандарт определяет обработку для вычисления произведений на следующие константы:

y~y*113/128,

z~y*719/4096

и выполняется следующим образом:

x2=(x>>3)-(x>>7);x3=x2-(x>>11);y=x2+(x3>>1);z=x-x2;

Фиг.4 показывает блок-схему кодирующей системы 400, которая может включать в себя преобразования, реализующие двоичные дроби, имеющие знакосимметричные ошибки округления, как описано выше. Устройство захвата/память 410 может принимать сигнал источника, выполнять преобразование в цифровой формат и обеспечивает входные/исходные данные. Устройство 410 захвата может быть видеокамерой, цифровым преобразователем или каким-либо другим устройством. Процессор 420 обрабатывает исходные данные и генерирует сжатые данные. Внутри процессора 420 исходные данные могут преобразовываться посредством блока 422 DCT, сканироваться посредством блока 424 зигзагообразного сканирования, квантоваться посредством блока 426 квантования, кодироваться посредством статистического кодировщика 428 и пакетироваться посредством блока 430 пакетирования. Блок 422 DCT может выполнять 2D преобразования DCT над исходными данными в соответствии со способами, здесь описанными, и может поддерживать как полные, так и масштабированные интерфейсы. Каждый из блоков 422 по 430 может реализовываться в аппаратном обеспечении, встроенном программном обеспечении и/или программном обеспечении. Например, блок 422 DCT может реализовываться со специализированным аппаратным обеспечением, набором инструкций для арифметико-логического блока (ALU) и т.д.

Блок 440 хранения может хранить сжатые данные из процессора 420. Передатчик 442 может передавать сжатые данные. Контроллер/процессор 450 управляет работой различных блоков в кодирующей системе 400. Память 452 хранит данные и программные коды для кодирующей системы 400. Одна или более шин 460 осуществляют взаимосвязь различных блоков в кодирующей системе 400.

Фиг.5 показывает блок-схему системы 500 декодирования, которая может включать в себя преобразования, реализующие двоичные дроби, имеющие знакосимметричные ошибки округления, как описано выше. Приемник 510 может принимать сжатые данные от кодирующей системы, и блок 512 хранения может хранить принятые сжатые данные. Процессор 520 обрабатывает сжатые данные и генерирует выходные данные. Внутри процессора 520 сжатые данные могут депакетироваться посредством блока 522 депакетирования, декодироваться посредством статистического декодера 524, обратным образом квантоваться посредством блока 526 обратного квантования, помещаться в должном порядке посредством блока 528 обратного зигзагообразного сканирования и преобразовываться посредством блока 530 IDCT. Блок 530 IDCT может выполнять 2D преобразования IDCT над полными или масштабированными коэффициентами преобразования в соответствии со способами, здесь описанными, и может поддерживать как полные, так и масштабированные интерфейсы. Каждый из блоков 522 по 530 может реализовываться в аппаратном обеспечении, встроенном программном обеспечении и/или программном обеспечении. Например, блок 530 IDCT может реализовываться специализированным аппаратным обеспечением, набором инструкций для ALU и т.д.

Устройство 540 отображения отображает реконструированные изображения и видео из процессора 520. Контроллер/процессор 550 управляет работой различных блоков в системе 500 декодирования. Память 552 хранит данные и программные коды для системы 500 декодирования. Одна или более шин 560 взаимно связывают различные блоки в системе 500 декодирования.

Процессоры 420 и 520 могут каждый реализовываться с одной или более специализированными интегральными схемами (ASIC) цифровых сигнальных процессоров (DSP) и/или некоторым другим типом процессоров. Альтернативно, процессоры 420 и 520 могут каждый заменяться одним или более оперативными запоминающими устройствами (RAM), постоянными запоминающими устройствами (ROM), электрическими программируемыми ROM (EPROM), электрически стираемыми программируемыми ROM (EEPROM), магнитными дисками, оптическими дисками и/или другими типами энергозависимых и энергонезависимых устройств памяти, известных в данной области техники.

Варианты осуществления, здесь описанные, могут реализовываться посредством аппаратного обеспечения, программного обеспечения, встроенного программного обеспечения, промежуточного программного обеспечения, микрокода или любой комбинации перечисленного. Когда системы и/или способы реализуются в программном обеспечении, встроенном программном обеспечении, промежуточном программном обеспечении или микрокоде, программном коде или кодовых сегментах, они могут храниться в машиночитаемом носителе, таком как компонент хранения. Кодовый сегмент может представлять процедуру, функцию, подпрограмму, программу, процедуру, подпроцедуру, модуль, программный пакет, класс или любую комбинацию инструкций, структур данных или программных операторов. Кодовый сегмент может соединяться с другим кодовым сегментом или аппаратной схемой посредством пересылки и/или приема информации, данных, аргументов, параметров, или содержимого памяти. Информация, аргументы, параметры, данные и т.д. могут пересылаться, посылаться или передаваться с использованием любых подходящих средств, включающих в себя совместное использование памяти, передачу сообщений, передачу маркеров, сетевую передачу и т.д.

Для программного варианта реализации, способы, здесь описанные, могут реализовываться модулями (например, процедурами, функциями и так далее), которые выполняют функции, здесь описанные. Программные коды могут храниться в запоминающих устройствах и исполняться процессорами. Запоминающее устройство может реализовываться внутри процессора или вне процессора, в этом случае оно может быть коммуникативно соединено с процессором посредством различных средств, как известно в данной области техники.

Этапы способа или алгоритма, описанные в связи с вариантами осуществления, здесь раскрытыми, могут осуществляться напрямую в аппаратном обеспечении, в программном модуле, исполняемом процессором, или в комбинации упомянутых двух. Программный модуль может находиться в оперативном запоминающем устройстве ("RAM"), флэш-памяти, постоянном запоминающем устройстве ("ROM"), стираемом программируемом постоянном запоминающем устройстве ("EPROM"), электронно-перепрограммируемой постоянной памяти ("EEPROM"), регистрах, жестком диске, съемном диске, CD-ROM или любой другой форме запоминающего носителя, известного в данной области техники. Иллюстративный запоминающий носитель соединен с процессором, так что процессор может считывать информацию с и записывать информацию на запоминающий носитель. В альтернативе, запоминающий носитель может быть объединенным с процессором. Процессор и запоминающий носитель могут находиться в связанной с конкретным приложением пользовательской схеме ("ASIC"). ASIC может находиться в пользовательском терминале. В альтернативе, процессор и запоминающий носитель могут находиться как дискретные компоненты в пользовательском терминале.

Следует отметить, что способы, здесь описанные, могут реализовываться на многообразии аппаратного обеспечения, процессоров и систем, известных специалистам в данной области техники. Например, машина, которая используется в варианте реализации, может иметь дисплей, чтобы отображать содержимое и информацию, процессор, чтобы управлять работой клиента, и память для хранения данных и программ, относящихся к работе машины. В некоторых вариантах реализации, машина является сотовым телефоном. В некоторых вариантах реализации, машина является карманным компьютером или телефонной трубкой, имеющей возможности осуществления связи. В другом варианте реализации, машина является персональным компьютером, имеющим возможности осуществления связи.

Различные иллюстративные логики, логические блоки, модули и схемы, описанные в соединении с вариантами реализации, здесь раскрытыми, могут реализовываться или выполняться с процессором общего назначения, DSP, ASIC, программируемой пользователем вентильной матрицей (FPGA) или другим программируемым логическим устройством, дискретным логическим элементом или транзисторной логикой, дискретными аппаратными компонентами или любой комбинацией перечисленного, сконструированной, чтобы выполнять функции, здесь описанные. Процессор общего назначения может быть микропроцессором, но, в альтернативе, процессор может быть любым стандартным процессором, контроллером, микроконтроллером или конечным автоматом. Процессор может также реализовываться как комбинация вычислительных устройств, например комбинация DSP и микропроцессора, множество микропроцессоров, один или более микропроцессоров в соединении с ядром DSP, или любая другая такая конфигурация.

Хотя сущность была описана на языке, конкретном для структурных признаков и/или методологических действий, следует понимать, что предмет изобретения, определенный в приложенных пунктах формулы изобретения, не является необходимо ограниченным конкретными признаками или действиями, описанными выше. Скорее, конкретные признаки и действия, описанные выше, раскрыты как иллюстративные формы реализации пунктов формулы изобретения.

1. Способ определения алгоритма для вычисления двух или более произведений целочисленного значения х и аппроксимаций двух или более иррациональных значений, используя процессор, способ, содержащий:прием процессором целочисленного значения х;определение процессором набора двоичных дробей a₁/2^b…a_m/2^b, аппроксимирующих два или более иррациональных значения;определение процессором последовательности промежуточных значений w₁…w_t, чтобы вычислять два или более произведения посредством:установки w₁ равным целочисленному значению х; иопределения w₂…w_t в соответствии с (а) по меньшей мере, одним из: w₁…w_t-1 и (b) одним из: операции плюс, операции минус и операции сдвига вправо;определение процессором индексов l₁…l_m≤t промежуточных значений из последовательности промежуточных значений w₁…w_t, которые соответствуют двум или более произведениям, так что:w_1l≈х·а₁/2^b…w_1m≈x·a_m/2^b, иопределение процессором алгоритма посредством определения последовательности промежуточных значений w₁…w_t и определения индексов l₁…l_m≤t промежуточных значений из последовательности промежуточных значений w₁…w_t.

2. Способ по п.1, дополнительно содержащий:определение последовательности промежуточных значений w₁…w_t в соответствии с одним или более из: метрики средней асимметрии, метрики средней ошибки, метрики дисперсии ошибки и метрики величины ошибки.

3. Способ по п.2, дополнительно содержащий:оценку эффективности обработки последовательности промежуточных значений w₁…w_t на основе результата наихудшего случая одного или более из: метрики средней асимметрии, метрики средней ошибки, метрики дисперсии ошибки и метрики величины ошибки.

4. Способ по п.1, дополнительно содержащий:определение последовательности промежуточных значений w₁…w_t, имеющих наименьшее количество суммирований.

5. Способ по п.1, дополнительно содержащий:определение последовательности промежуточных значений w₁…w_t, имеющих наименьшее количество сдвигов вправо.

6. Способ по п.1, дополнительно содержащий:определение последовательности промежуточных значений w₁…w_t, имеющих наименьшее количество суммирований и правых сдвигов.

7. Способ по п.6, дополнительно содержащий:определение промежуточных значений из последовательности промежуточных значений w₁…w_t, имеющих наименьшее число суммирований и сдвигов вправо, имеющих наименьшее количество суммирований.

8. Способ по п.1, в котором определение w₂…w_t дополнительно содержит:задание члена w_k последовательности промежуточных значений w₁…w_t как имеющего одно из значений w_i>>s_k, -w_i, w_i+w_j или w_i-w_j,где s_k - это количество бит, чтобы осуществлять сдвиг вправо для w_i, i меньше, чем k, и j меньше, чем k.

9. Способ по п.1, дополнительно содержащий:определение последовательности промежуточных значений w₁…w_t как знакосимметричной последовательности, минимизирующей метрику средней асимметрии.

10. Машиночитаемый носитель, содержащий исполнимые инструкции, чтобы выполнять способ определения алгоритма для вычисления двух или более произведений целочисленного значения x и аппроксимаций двух или более иррациональных значений, используя процессор, содержащий инструкции для:приема целочисленного значения x;определения набора двоичных дробей a₁/2^b…a_m/2^b, аппроксимирующих два или более иррациональных значения;определения последовательности промежуточных значений w₁…w_t;определения индексов l₁…l_m≤t промежуточных значений из последовательности промежуточных значений w₁…w_t, которые соответствуют двум или более произведениям, так что:w_1l≈х·а₁/2^b…w_1m≈x·a_m/2^b; иопределения алгоритма посредством определения последовательности промежуточных значений w₁…w_t и определения индексов l₁…l_m≤t промежуточных значений из последовательности промежуточных значений w₁…w_t.

11. Машиночитаемый носитель по п.10, дополнительно содержащий инструкции для:определения последовательности промежуточных значений w₁…w_t в соответствии с одним или более из: метрики средней асимметрии, метрики средней ошибки, метрики дисперсии ошибки и метрики величины ошибки.

12. Машиночитаемый носитель по п.11, дополнительно содержащий инструкции для:установки w₁ равным целочисленному значению x; иопределения w₂…w_t в соответствии с (а) одним из: w₁…w_t-1 и (b) одного из: операции плюс, операции минус и операции сдвига вправо.

13. Машиночитаемый носитель по п.11, дополнительно содержащий инструкции для:оценки эффективности обработки последовательности промежуточных значений w₁…w_t на основе результата наихудшего случая одного или более из: метрики средней асимметрии, метрики средней ошибки, метрики дисперсии ошибки и метрики величины ошибки.

14. Машиночитаемый носитель по п.10, дополнительно содержащий инструкции для выполнения одного или более из:определения последовательности промежуточных значений w₁…w_t, имеющих наименьшее количество суммирований; иопределения последовательности промежуточных значений w₁…w_t, имеющих наименьшее количество сдвигов.

15. Устройство преобразования цифровых сигналов, содержащее:каскад масштабирования, который масштабирует коэффициенты DCT в соответствии со строковым преобразованием и столбцовым преобразованием, и который предварительно назначает предопределенное количество битов точности коэффициентам DCT;каскад преобразования, который преобразует коэффициенты DCT с использованием знакосимметричных двоичных рациональных аппроксимаций констант преобразования и выводит преобразованные коэффициенты DCT; икаскад сдвига вправо, который сдвигает преобразованные коэффициенты DCT, чтобы определять выходные преобразованные коэффициенты DCT.

16. Устройство по п.15, дополнительно содержащее каскад смещения DC, который изменяет коэффициент смещения DC перед тем, как каскад преобразования преобразовывает коэффициенты DCT, чтобы корректировать ошибки округления.

17. Устройство по п.15, в котором выходные преобразованные коэффициенты DCT содержат ГОСТ коэффициенты.

18. Устройство по п.15, в котором знакосимметричные двоичные рациональные аппроксимации констант преобразования используют промежуточные значения w₁…w_t, определенные посредством (а) установки w₁ равным входному целочисленному значению и (b) определения w₂…w₁ в соответствии с одним из: w₁…w_t-1 и одним из: операции плюс, операции минус и операции сдвига вправо.

19. Устройство для определения алгоритма для вычисления двух или более произведений целочисленного значения х и аппроксимаций двух или более иррациональных значений, содержащее:средство для приема целочисленного значения х;средство для определения набора двоичных дробей a₁/2^b…a_m/2^b, аппроксимирующих два или более иррациональных значения;средство для определения последовательности промежуточных значений w₁…w_t;средство для определения индексов l₁…l_m≤t промежуточных значений из последовательности промежуточных значений w₁…w_t, которые соответствуют двум или более произведениям, так что:w_1l≈х·а₁/2^b…w_1m≈x·a_m/2^b, исредство для определения алгоритма посредством определения последовательности промежуточных значений w₁…w_t и определения индексов l₁…l_m≤t промежуточных значений из последовательности промежуточных значений w₁…w_t.

20. Устройство по п.19, в котором средство для определения последовательности промежуточных значений w₁…w_t содержит средство для определения последовательности в соответствии с одним или более из: метрики средней асимметрии, метрики средней ошибки, метрики дисперсии ошибки и метрики величины ошибки.

21. Устройство по п.19, в котором средство для определения последовательности промежуточных значений