Арочная цилиндрическая зубчатая передача

Арочная цилиндрическая зубчатая передача

Иллюстрации

Показать все

Реферат

Изобретение относится к деталям машин, а именно к зубчатым передачам внешнего зацепления, состоящим из двух цилиндрических колес с параллельными осями и с зубьями, имеющими арочные продольные и эвольвентные поперечные профили.

Известна цилиндрическая зубчатая передача, состоящая из двух цилиндрических зубчатых колес с зубьями, имеющими арочные продольные и эвольвентные поперечные профили [А.с. 785569 СССР, МПК3 F16H 1/08. Цилиндрическая зубчатая передача / Сидоренко А.К. - 2693172/25-28; заявл. 06.12.1978; опубл. 07.12.1980, бюл. №45. - 5 с.] - прототип.

В известной зубчатой передаче исходные производящие контуры зубчатых колес не имеют смещения, а угол зацепления имеет стандартное значение. В такой передаче при числе зубьев, меньшем , диаметры основных цилиндров колес имеют значения, большие значений диаметров цилиндров нижних точек активного профиля, которые равны , где m - модуль зубьев, z - число зубьев колеса, - коэффициент высоты головки зуба, α - угол зацепления зубчатой передачи. Вследствие этого боковые поверхности зубьев таких колес имеют неэвольвентные участки, расположенные ниже основного цилиндра, а именно между основным цилиндром и цилиндром нижних точек активного профиля. Наличие этих участков снижает технологичность конструкции зубчатой передачи.

Эвольвентные участки боковых поверхностей зубьев, расположенные выше основного цилиндра, обрабатывают при помощи вращающегося инструмента, режущие участки которого выполнены параллельно оси его вращения, а ось вращения расположена в плоскости симметрии зубчатого венца, например, при помощи резцовой головки, главные режущие кромки резцов которой расположены параллельно оси ее вращения. В процессе обкатки профилирующие точки резцов расположены в плоскости, касательной к основному цилиндру, а саму резцовую головку перемещают в плоскости симметрии зубчатого венца в направлении, перпендикулярном оси вращения головки.

Для обработки участков, расположенных ниже основного цилиндра, а именно между основным цилиндром и цилиндром нижних точек активного профиля, необходимо выполнять дополнительную операцию, что увеличивает трудоемкость изготовления колес. Кроме того, чтобы избежать заклинивания зубьев малого колеса с головками зубьев большого колеса, эти участки необходимо обрабатывать с подрезанием ножки зуба. Подрезание снижает прочность зубьев, сокращает продолжительность нахождения зубьев в зацеплении, снижает плавность работы зубчатой передачи.

Предлагаемое изобретение направлено на повышение технологичности конструкции зубчатой передачи за счет создания такой зубчатой передачи, у обоих колес которой основные цилиндры расположены между цилиндрами нижних точек активного профиля и цилиндрами впадин.

Для решения этой задачи в арочной цилиндрической зубчатой передаче, состоящей из двух - малого и большого - цилиндрических зубчатых колес с зубьями, имеющими арочные продольные и эвольвентные поперечные профили, согласно изобретению исходный производящий контур малого колеса смещен от оси вращения малого колеса, а исходный производящий контур большого колеса смещен к оси вращения большого колеса, абсолютные значения смещений исходных производящих контуров колес равны между собой и равны произведению коэффициента смещения x на модуль зубьев, при этом коэффициент смещения x имеет значение, являющееся одним из решений неравенства:

,

а угол зацепления α зубчатой передачи имеет значение, являющееся одним из решений системы неравенств:

где z₁ - число зубьев малого колеса, z₂ - число зубьев большого колеса, - коэффициент высоты головки зуба, c* - коэффициент радиального зазора.

При этом коэффициент смещения x и угол зацепления α имеют такие значения, при которых величина, равная половине суммы толщин зубьев малого и большого колес по окружностям вершин в сечениях, перпендикулярных осям колес, больше или равна минимально допустимому значению толщины зуба по окружности вершин.

При необходимости толщину зубьев малого колеса увеличивают, а толщину зубьев большого колеса уменьшают, при этом величина ΔS, на которую увеличивают толщину зубьев малого колеса по делительной окружности в сечении, перпендикулярном оси колеса, равна величине, на которую уменьшают толщину зубьев большого колеса по делительной окружности в сечении, перпендикулярном оси колеса. Боковая поверхность каждого зуба после изменения его толщины образована боковой поверхностью зуба до изменения его толщины, повернутой относительно оси вращения колеса на угол, равный отношению ΔS к радиусу делительной окружности колеса.

Величина ΔS, на которую изменяют толщины зубьев колес, имеет такое значение, при котором толщины зубьев каждого из колес по окружностям вершин в сечениях, перпендикулярных осям колес, больше или равны минимально допустимому значению толщины зуба по окружности вершин, а площади поперечных сечений зубьев малого и большого колес равны между собой.

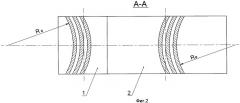
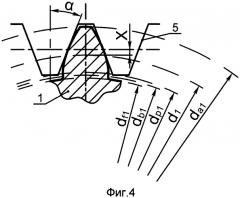
Сущность изобретения поясняется чертежами. На фиг.1 изображена предлагаемая зубчатая передача, поперечный разрез по плоскости симметрии зубчатого венца; на фиг.2 - разрез А-А по фиг.1; на фиг.3 показано расположение основного цилиндра у зубчатого колеса с числом зубьев, меньшим , без смещения исходного производящего контура; на фиг.4 показано расположение основного цилиндра у зубчатого колеса с числом зубьев, меньшим , после смещения исходного производящего контура и изменения угла зацепления; на фиг.5 показано расположение основного цилиндра у зубчатого колеса с числом зубьев, большим , без смещения исходного производящего контура; на фиг.6 показано расположение основного цилиндра у зубчатого колеса с числом зубьев, большим , после смещения исходного производящего контура и изменения угла зацепления; на фиг.7 изображен поперечный разрез зубьев малого колеса после увеличения толщины зубьев; на фиг.8 - поперечный разрез зуба большого колеса после уменьшения толщины зубьев; на фиг.9, 10 показаны различные случаи расположения области допустимых значений угла зацепления α в зависимости от коэффициента смещения х исходных производящих контуров; на фиг.11 - разрез Б-Б по фиг.7; на фиг.12 - выносной элемент B с фиг.11.

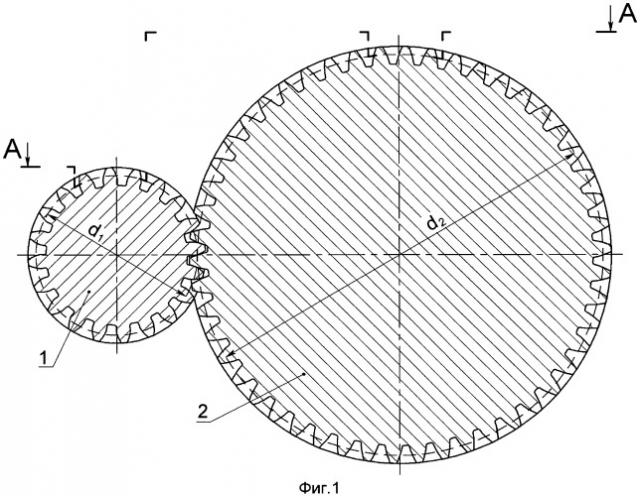
Предлагаемая арочная цилиндрическая зубчатая передача состоит из малого 1 и большого 2 цилиндрических колес с зубьями, имеющими арочные продольные и эвольвентные поперечные профили. d₁ и d₂ - диаметры делительных цилиндров колес.

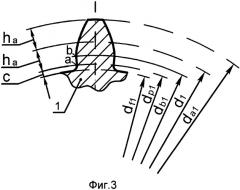
При отсутствии смещения исходного производящего контура, стандартном значении угла зацепления и числе зубьев, меньшем , диаметр основного цилиндра малого колеса d_b1 имеет значения, большие значений диаметра цилиндра нижних точек активного профиля d_p1 и боковые поверхности зубьев малого колеса имеют неэвольвентные участки а-b, расположенные ниже основного цилиндра, а именно между основным цилиндром и цилиндром нижних точек активного профиля (см. фиг.3). Дополнительная операция по обработке этих неэвольвентных участков увеличивает трудоемкость изготовления колес.

С другой стороны, при отсутствии смещения исходного производящего контура, стандартном значении угла зацепления и числе зубьев, большем , диаметр основного цилиндра большого колеса d_b2 имеет значения, меньшие значений диаметра цилиндра впадин d_f2 (см. фиг.5), что также нежелательно. В процессе обработки эвольвентных участков b-d боковых поверхностей зубьев профилирующие точки 3 резцов 4 резцовой головки расположены в плоскости A, касательной к основному цилиндру колеса (см. фиг.7). Поэтому в том случае, когда d_b2<d_f2, нарезаются зубья, имеющие высоту, большую стандартного значения высоты зуба, что снижает прочность зуба.

Для того чтобы основные цилиндры обоих колес были расположены между цилиндрами нижних точек активного профиля и цилиндрами впадин, исходный производящий контур 5 малого колеса смещен от оси вращения малого колеса (см. фиг.4), а исходный производящий контур 6 большого колеса смещен к оси вращения большого колеса (см. фиг.6). Абсолютные значения смещений X исходных производящих контуров колес равны между собой и равны произведению коэффициента смещения x на модуль зубьев m. Коэффициент смещения x имеет значение, являющееся одним из решений неравенства:

,

где z₁ - число зубьев малого колеса, z₂ - число зубьев большого колеса, - коэффициент высоты головки зуба, c* - коэффициент радиального зазора.

Угол зацепления α зубчатой передачи имеет значение, являющееся одним из решений системы неравенств:

Использование коэффициента смещения x и угла зацепления α, являющихся решениями вышеуказанных неравенств, позволяет обеспечить одновременное выполнение условии: , где:

d_f1 - диаметр цилиндра впадин малого колеса, вычисляемый по формуле:

;

d_b1 - диаметр основного цилиндра малого колеса: d_b1=m·z₁·cosα;

d_p1 - диаметр цилиндра нижних точек активного профиля малого колеса:

;

d_f2 - диаметр цилиндра впадин большого колеса:

;

d_b2 - диаметр основного цилиндра большого колеса: d_b2=m·z₂·cosα;

d_p2 - диаметр цилиндра нижних точек активного профиля большого колеса:

Модуль зубьев m рассчитывается по формуле m=2·a _w/(z₁+z₂), где a _w - межосевое расстояние, и может иметь любое значение: не только целое, но и дробное.

На фиг.9 показано расположение области допустимых значений угла зацепления α в зависимости от коэффициента смещения х исходных производящих контуров, где , ,

На отрезке AG расположены значения угла зацепления α, равные при которых выполняется условие d_b1=d_p1. На отрезке EC расположены значения угла зацепления α, равные при которых выполняется условие d_b1=d_f1. На отрезке HC расположены значения угла зацепления α, равные при которых выполняется условие d_b2=d_p2. На отрезке AF расположены значения угла зацепления α, равные при которых выполняется условие d_b2=d_f2.

Таким образом, точка А соответствует одновременному выполнению условий d_b1=d_p1 и d_b2=d_f2, точка B - выполнению условий d_b1=d_f1 и d_b2=d_f2, точка C - выполнению условий d_b1=d_f1 и d_b2=d_p2, точка D - выполнению условий d_b1=d_p1 и d_b2=d_p2.

Область допустимых значений угла зацепления α в зависимости от коэффициента смещения x исходных производящих контуров расположена внутри заштрихованного четырехугольника ABCD.

В том случае, когда x_min≤0, т.е. когда существуют такие значения угла зацепления α, находящиеся в диапазоне от до (см. фиг.10), при которых можно обеспечить выполнение условий без смещения исходных производящих контуров колес, т.е. при x=0.

При смещении исходного производящего контура малого колеса от оси вращения малого колеса толщина его зубьев по окружности вершин S_a1 уменьшается и при некоторых значениях коэффициента смещения х и угла зацепления α она может стать меньше минимально допустимого значения толщины зуба по окружности вершин [S_a]. Для того чтобы этого не произошло, толщину зубьев малого колеса увеличивают, а толщину зубьев большого колеса уменьшают. При этом величина ΔS, на которую увеличивают толщину зубьев малого колеса по делительной окружности в сечении, перпендикулярном оси колеса (см. фиг.7), равна величине ΔS, на которую уменьшают толщину зубьев большого колеса по делительной окружности в сечении, перпендикулярном оси колеса (см. фиг.8). Боковая поверхность Г каждого зуба после изменения его толщины образована боковой поверхностью Д зуба до изменения его толщины, повернутой относительно оси вращения колеса на угол, равный отношению ΔS к радиусу делительного цилиндра колеса: r₁ или r₂ соответственно. r₁=d₁/2, r₂=d₂/2.

Для того чтобы иметь возможность изменять толщину зубьев, выбирают такие значения коэффициента смещения х и угла зацепления α, при которых величина, равная половине суммы толщин зубьев малого и большого колес по окружностям вершин в сечениях, перпендикулярных осям колес, больше или равна минимально допустимому значению толщины зуба по окружности вершин:

0,5·(S_а1+S_а2)≥[S_a]

Значение ΔS, на которую изменяют толщины зубьев колес, подбирают таким образом, чтобы толщины зубьев каждого из колес по окружностям вершин в сечениях, перпендикулярных осям колес, после изменения их толщины были больше или равны минимально допустимому значению толщины зуба по окружности вершин:

S_a1+ΔS_a1≥[S_a]

S_a2-ΔS_a2≥[S_a]

Для того чтобы зубья малого и большого колес имели одинаковую прочность, подбирают такое значение ΔS, при котором площади поперечных сечений зубьев малого и большого колес равны между собой.

Чем больше ширина b зубчатого венца колеса при одном и том же радиусе арки зуба R_a, тем меньше делительная нормальная ширина впадины e_bn между зубьями, замеренная в плоскости, проходящей через точку E пересечения боковой поверхности зуба с основным цилиндром и с торцовой плоскостью зубчатого венца. При большой ширине b зубчатого венца существует опасность того, что в процессе обработки боковой поверхности зуба при помощи главной режущей кромки Ж резца 4 его вспомогательная режущая кромка И заденет боковую поверхность соседнего зуба. Чтобы этого не произошло, при проектировании зубчатой передачи необходимо проверять условие, чтобы ширина впадины e_bt1 между зубьями малого колеса, замеренная по хорде основного цилиндра в сечении, перпендикулярном оси колеса, была больше ширины S_bt режущей части резцов, замеренной в торцовом сечении зубчатого венца малого колеса.

Ширину впадины e_bt1 вычисляют по формуле:

e_bt1=2·r_b1·sin((π/2-2·x·tgα-ΔS/m-z₁·inνα)/z₁),

где r_b1 - радиус основного цилиндра малого колеса, m - модуль зубьев.

Ширину S_bt режущей части резцов вычисляют по формуле:

,

где S_br - ширина режущей части резцов в радиальном направлении, угол β вычисляют по формуле β=arcsin(b/(2·R_u))-arcsin(b/(2·R_u-2·S_br)), R_u - радиус окружности, на которой расположены профилирующие точки резцов резцовой головки, вычисляемый по формуле:

,

где R_a - радиус арки зуба, равный радиусу развертки линии смещения исходного контура на плоской развертке делительного цилиндра, b - ширина зубчатого венца малого колеса.

В том случае, когда e_bt1>S_bt, вспомогательная режущая кромка И резца 4 не заденет боковую поверхность соседнего зуба.

Таким образом, использование зубчатых колес со смещенными исходными производящими контурами и с углом зацепления, являющимся одним из решений вышеприведенной системы неравенств, позволяет создать такую арочную зубчатую передачу, у обоих колес которой основные цилиндры расположены между цилиндрами нижних точек активного профиля и цилиндрами впадин. У боковых поверхностей зубьев таких колес отсутствуют неэвольвентные участки, расположенные между основным цилиндром и цилиндром нижних точек активного профиля. Это повышает технологичность конструкции зубчатой передачи.

1. Арочная цилиндрическая зубчатая передача, состоящая из двух - малого и большого - цилиндрических колес с зубьями, имеющими арочные продольные и эвольвентные поперечные профили, отличающаяся тем, что исходный производящий контур малого колеса смещен от оси вращения малого колеса, а исходный производящий контур большого колеса смещен к оси вращения большого колеса, абсолютные значения смещений исходных производящих контуров колес равны между собой и равны произведению коэффициента смещения x на модуль зубьев, при этом коэффициент смещения x имеет значение, являющееся одним из решений неравенства: а угол зацепления α зубчатой передачи имеет значение, являющееся одним из решений системы неравенств: где z₁ - число зубьев малого колеса, z₂ - число зубьев большого колеса, -коэффициент высоты головки зуба, с* - коэффициент радиального зазора.

2. Зубчатая передача по п.1, отличающаяся тем, что коэффициент смещения x и угол зацепления α имеют такие значения, при которых величина, равная половине суммы толщин зубьев малого и большого колес по окружностям вершин в сечениях, перпендикулярных осям колес, больше или равна минимально допустимому значению толщины зуба по окружности вершин.

3. Зубчатая передача по п.2, отличающаяся тем, что толщины зубьев малого колеса увеличены, а толщины зубьев большого колеса уменьшены, при этом величина ΔS, на которую увеличены толщины зубьев малого колеса по делительной окружности в сечении, перпендикулярном оси колеса, равна величине, на которую уменьшены толщины зубьев большого колеса по делительной окружности в сечении, перпендикулярном оси колеса, а боковая поверхность каждого зуба после изменения его толщины образована боковой поверхностью зуба до изменения его толщины, повернутой относительно оси вращения колеса на угол, равный отношению величины ΔS к радиусу делительной окружности колеса.

4. Зубчатая передача по п.3, отличающаяся тем, что величина ΔS, на которую изменены толщины зубьев колес, имеет такое значение, при котором толщины зубьев каждого из колес по окружностям вершин в сечениях, перпендикулярных осям колес, больше или равны минимально допустимому значению толщины зуба по окружности вершин.

5. Зубчатая передача по п.4, отличающаяся тем, что величина ΔS, на которую изменены толщины зубьев колес, имеет такое значение, при котором площади поперечных сечений зубьев малого и большого колес равны между собой.

6. Зубчатая передача по п.5, отличающаяся тем, что коэффициент смещения x, угол зацепления α и величина ΔS, на которую изменены толщины зубьев колес, имеют такие значения, при которых ширина впадины е_bt1 между зубьями малого колеса, замеренная по хорде основного цилиндра в сечении, перпендикулярном оси колеса, больше ширины S_bt режущей части резцов резцовой головки, при помощи которой обрабатывают боковые поверхности зубьев, замеренной в торцовом сечении зубчатого венца малого колеса, при этом ширину впадины е_bt1 вычисляют по формуле:e_bt1=2·r_b1·sin((π/2-2·x·tgα-ΔS/m-z₁·inνα)/z₁,где r_b1 - радиус основного цилиндра малого колеса, m - модуль зубьев, а ширину S_bt режущей части резцов вычисляют по формуле: где S_br - ширина режущей части резцов в радиальном направлении, угол β вычисляют по формуле β=arcsin(b/(2·R_u))-arcsin(b/(2·R_u-2-S_br)), R_u - радиус окружности, на которой расположены профилирующие точки резцов резцовой головки, вычисляемый по формуле: где R_a - радиус арки зуба, равный радиусу развертки линии смещения исходного контура на плоской развертке делительного цилиндра, b - ширина зубчатого венца малого колеса.