Способ и устройство выбора стратегии целераспределения по групповым объектам

Способ и устройство выбора стратегии целераспределения по групповым объектам

Иллюстрации

Показать все

Реферат

Изобретение относится к цифровой вычислительной технике, а именно к цифровым вычислительным системам для обработки входной информации о характеристиках боевых средств, ее преобразовании, выбора необходимой стратегии, формирования критериев противоборства с выявлением результатов боевых действий (победа, поражение, паритет), оценки своих потерь и нанесенного противнику ущерба, оценки влияния наличия и отсутствия разведки о координатах боевых средств на результаты боевых действий, выявления ситуаций, при которых выбор стратегии не дает боевого эффекта, может быть использовано командным составом Вооруженных Сил в процессе его обучения и переучивания, проведения командно-штабных учений и непосредственно для планирования групповых боевых действий (ГБД). Техническим результатом является расширение арсенала технических средств за счет создания способа и устройства выбора стратегии целераспределения по групповым объектам.

Известен способ [1-4], который раскрывает динамику боя и позволяет до его проведения назвать будущего победителя. Однако не известен способ ведения боевых действий (БД) против разнородных группировок с оценкой его результативности. В приведенных источниках, во-первых, не рассматривается БД против стороны, состоящей из группировок, включающих разнородные боевые средства (БСр) с неодинаковыми характеристиками, поэтому не может быть приведен и выбор правильной стратегии групповых БД. Во-вторых, не оценивается цена достигнутой победы, отсутствует количественная оценка нанесения максимального ущерба противнику при победе или поражении от него. Третьим недостатком при ведении боя является существующее смещение акцентов в сторону отношения количества БСр сторон, а не отношения интенсивностей ведения огня сторонами, которое приводит к снижению боевой эффективности и даже к поражению стороны А при групповых БД (ГБД).

Известен способ [5], устраняющий эти недостатки, но он не в полной мере учитывает специфику ведения ГБД. Во-первых, учет разнородности не только БСр сторон, но и профессионального уровня личного состава при управлении этой техникой, например использование складок местности для скрытности, наличие боевого опыта, слаженности и др. факторов, приводит к разным вероятностям p_1A≠p_2A поражения БСр и разным скорострельностям f_1A≠f_2A одних и тех же БСр стороной А. Отсюда возникает и неравенство интенсивностей µ₁≠µ₂ ведения поражающего огня боевыми средствами по группировкам B₁ и В₂. Таким образом, учет не только разновидностей видов БСр: самолетов, вертолетов, орудий, танков, ракет и т.д., но и разной подготовленности, слаженности, опыта и профессионализма личного состава всех сторон, приводит к более адекватной модели ведения ГБД.

Вторым недостатком служит то обстоятельство, что в способе [5] не указаны ситуации, при которых использование любой из рассматриваемых стратегий не приводит к повышению эффективности (результативности) боевых действий.

Третьим недостатком способа [5] является факт не учета, при котором известен вид, состав БСр группировок противника, но не известны координаты их расположения. В этой ситуации возникает необходимость в выборе другой стратегии ведения ГБД.

Имеются патенты [6-9], направленные на создание аппаратуры приема и реализации целеуказания, которые не устраняют выявленные недостатки и не решают сформулированную авторами задачу.

Поэтому возникает потребность в разработке такого способа и устройства, которые позволили бы устранить отмеченные недостатки.

В отличие от известных способов ведения ГБД повышение боевой эффективности (результативности) в предлагаемом изобретении осуществляется за счет:

- учета как разнородности БСр, так и квалификации личного состава обеих сторон;

- выбора оптимальной стратегии ведения ГБД при наличии информации о координатах БСр группировок противника, так и при ее отсутствии;

- оценки исхода предстоящих боевых действий до их проведения, прогнозирования цены победы над противником (оценки своих потерь), в случае поражения - нанесения максимального ущерба противнику с определением количества оставшихся у него непораженных БСр;

- выявления ситуаций, при которых выбор стратегии не приводит к повышению боевой эффективности (результативности) в ГБД;

- выбора рациональной стратегии и оценки результативности ГБД как при наличии, так и при отсутствии информации о координатах БСр в ГБД.

Согласно изобретению технический результат достигается тем, что коммутируют данные своих боевых средств и средств каждой группировки противника, записывают их в блок памяти, в который записывают наличие или отсутствие информации о координатах боевых средств сторон, которая поступает в блок логики, информацию о количественных и качественных характеристиках всех боевых средств передают на входы всех арифметических блоков и на блок умножения, с выхода которого произведения интенсивности поражающего огня стороны А на интенсивность каждой из группировок противника сравнивают в первом блоке сравнения с таким же произведением интенсивности поражающего огня стороны А с другой из группировок противника, результаты сравнения поступают на блок визуализации, считывание с которого определяет стратегию ведения боевых действий, величину критерия противоборства вычисляют в первом арифметическом блоке, сравнивают ее во втором блоке сравнения с пороговыми значениями, результаты сравнения подают на блок визуализации, считывание которых определяет исход боевых действий, остатки своих боевых средств или средств противника вычисляют соответственно во втором и третьем арифметическом блоке и осуществляют их считывание с блока визуализации, при отсутствии информации о координатах боевых средств сторон рациональной стратегией будут одноэтапные боевые действия, считываемые с блока визуализации, величину критерия противоборства вычисляют в первом арифметическом блоке, сравнивают ее во втором блоке сравнения с пороговыми значениями, результаты сравнения подают на блок визуализации, считывание которых определяет исход боевых действий, остатки своих боевых средств или средств противника вычисляют соответственно во втором и третьем арифметическом блоках и осуществляют их считывание с блока визуализации.

Сущность способа заключается в следующем.

Известно математическое описание двустороннего боя с помощью дифференциальных уравнений динамики боя [1-4]. При этом каждая из двух сторон А и В содержит группировку из однородных боевых средств (БСр).

Представляет интерес рассмотрение двусторонних БД с разнородными группировками, когда сторона А имеет однородные БСр, но личный состав по-разному подготовлен µ₁≠µ₂ к поражению каждой из группировок противника. Противостоящая ей сторона В включает две разнородные группировки В₁ и В₂. Показателями БСр стороны А до начала групповых БД будут:

М - первоначальное количество боевых средств;

µ₁=p_1Af_1A, µ₂=p_2Af_2A - интенсивности поражающего огня БСр, пропорциональные вероятностям поражения целей одним выстрелом p_1A, p_2A и скорострельностям БСр f_1A, f_2A, осуществляемые стороной А по БСр группировок B₁ и В₂.

В процессе ГБД (t>0) убывающая величина М в момент времени t обозначается m(t).

Группировки B₁ и В₂ имеют аналогичные показатели: N₁, λ₁=p₁f₁, n₁(t) и N₂, λ₂=p₂f₂, n₂(t) ведения БД по БСр стороны А.

При одновременном начале боя стороной А с группировками B₁ и В₂ в зависимости от исходных данных возникают следующие проблемные вопросы:

1) на чьей стороне будет победа?

2) существует ли критерий (математическое выражение), подставив в которое исходные данные до начала ГБД, можно ответить на первый вопрос?

3) какой стратегии целераспределения придерживаться стороне А при наличии или отсутствии информации о координатах БСр и как влияет она на результативность ГБД?

4) какой ценой досталась победа, т.е. сколько осталось БСр у победившей стороны?

5) в случае поражения стороны А, какая ее стратегия приводит к нанесению максимального ущерба противнику, и каков он?

6) в каких ситуациях выбор стратегии не дает эффекта?

В существующей литературе [1-4] при ведении БД между двумя сторонами с однородными БСр ответы на первые два вопроса имеются. Наличие двух разнородных группировок B₁ и В₂ у стороны В затрудняет получение ответа на все поставленные вопросы.

Стратегии планирования групповых боевых действий (ГБД) и их классификация. Рассмотрим следующие стратегии ведения ГБ:

а) стратегия двухэтапных ГБД, при которых сторона А на первом этапе выбирает стратегию S{A; B₁, B₂} - начинает всеми средствами уничтожать БСр группировки B₁(r₁=1) или другую стратегию S{A; B₂, B₁}, когда уничтожение начинается с группировки B₂(r₂=1), и всеми средствами ведет БД до ее полного уничтожения, на втором этапе оставшимися боевыми средствами она уничтожает другую группировку B₂(r₂=1) или B₁(r₁=1);

б) стратегия S{A; B₁∩B₂} одноэтапных групповых действий (ОГД), когда сторона А выбирает такое оптимальное относительное число r₁, что по группировке B₁ ведутся БД частью r₁m(t) своих БСр, а по группировке В₂ другой частью r₂m{t), где r₁+r₂=1. ГБД осуществляются до полного уничтожения обеих группировок (победы) или до своего поражения;

в) стратегия S{A; B₁∩B₂, B_о} смешанных групповых боевых действий (СГД), когда сторона А выбирает такое относительное (не оптимальное) число r₁ своих средств, когда по группировке B₁ ведутся БД частью r₁m(t) своих средств, а по группировке В₂ другой частью r₂m(t) БСр. Если одна из группировок будет уничтожена раньше (B₁ или В₂), то оставшимися средствами выводится из строя не оставшаяся группировка В_о.

Оптимальное ведение ГБД, во-первых, приводит к максимизации нанесения ущерба противнику, а во-вторых, к минимизации своих потерь.

Дифференциальные уравнения ГБД с разнородными группировками при наличии информации у сторон о координатах БСр. В отличие от БД с однородными группировками, в котором они осуществляются одноэтапно, в данном сценарии бой происходит в два этапа. Пусть на первом этапе ведутся БД с группировкой B₁, не обращая внимания на группировку В₂ (r₁=1, r₂=0; S{A; B₁, B₂}). Тогда дифференциальные уравнения, отражающие ГБД 1-го этапа во времени t₁, запишутся следующим образом:

Начальными условиями для 1-го этапа служат величины:

После уничтожения группировки B₁(N₁=0) сторона А на 2-м этапе приступает к уничтожению группировки B₂, при этом r₂=1 (r₁=0). Второму этапу t₂ соответствуют дифференциальные уравнения

Начальными условиями для второго этапа являются

Решение уравнений (1а, б) и (2а, б) с учетом начальных условий (1в) и (2в) приводит к получению формул (3а), (3б) для величин оставшихся БСр при победе стороны А в зависимости от выбранных стратегий ЦР S{A; B₁, B₂} или S{A; B₂, B₁}

Анализ выражений (3а) или (3б) позволяет конкретизировать выбор стратегии, не прибегая к их вычислению. Выполнение неравенства

осуществляется только при выполнении неравенства λ₁µ₁>λ₂µ₂, как и обратного при осуществлении λ₁µ₁<λ₂µ₂.

Это означает, что стратегия ДГБ заключается в уничтожении сначала группировки B_i, затем B_j, если λ_iµ_i>λ_jµ_j.

Критериями победы стороны А при использовании той или иной стратегии в ДГБ являются полученные путем преобразования формул (3а), (3б) неравенства

зависимые от квадратов локальных классических коэффициентов боевого превосходства:

- квадрата локального коэффициента боевого превосходства стороны A по отношению к группировке B₁;

- квадрата локального коэффициента боевого превосходства группировки B₂ по отношению к группировке B₁.

В формулах (4а) и (4б) также введены обозначения количественных соотношений N₁₂ группировок B₁ и B₂ и качественных λ₁₂, λ₂₁, а также соотношение интенсивностей µ₁₂ и µ₂₁, ведения огня стороной A по группировкам B₁, B₂ или В₂, B₁

Формулы (4а)-(4д) показывают, что критерии боевого превосходства (исхода предстоящих БД) К_п(R) определяются исходными данными: Д_А(М, p_1A, p_2A, f_1A, f_1A), Д_В1(N₁, p₁, f₁), Д_В2(N₂, p₂, f₂) сторон А и В при наличии разведки (R) о координатах БСр сторон.

При К_п(R)>1 фиксируется «Победа стороны А» и происходит вычисление в зависимости от выбранной стратегии одной из формул (3а) или (3б) величины оставшихся БСр стороны А М₂(А; В₁, В₂) или М₁(А; В₂, В₁) («Остаток БСр М₂=…» или «Остаток М₁=…»).

При неравенстве К_п(R)<1 - поражении стороны А, нанесенный ущерб стороне В определяется решением дифференциальных уравнений ГБД (формулы (1а, б, в) и (2а, б, в)). При победе стороны А на первом этапе и окончательном поражении на втором оставшееся число БСр у стороны В будет

Для данного сценария фиксируется информация: «Победа стороны В»; «Остаток БСр N₂=…» или «Остаток БСр N₁=…».

Для случая паритета сил и средств сторон А и В K_п(R)=1 фиксируется информация: «Паритет в ГБД».

Решение авторами разнообразных примеров для группировок с различными исходными данными (таблица 1) иллюстрирует преимущество предлагаемой авторами выбираемой стратегии двухэтапных БД, которая заключается в следующем.

В двухэтапных групповых действиях из всех k группировок для первоначального уничтожения выбирается i-я группировка, которой присуще условие

В двухэтапных БД первоначальное уничтожение начинается с 1-й группировки, если

λ₁µ₁>λ₂µ₂,

в противном случае, при

λ₁µ₁<λ₂µ₂,

уничтожение начинается со второй группировки.

В таблице 1 приведены примеры, подтверждающие правильность предложенной авторами стратегии как при победе стороны А, так и при поражении. При победе (см. строка 1б) сторона А сохраняет у себя 10 единиц БСр, при поражении - наносит противнику максимальный урон (строка 2а).

Таблица 1
Примеры, подтверждающие зависимость результатов БД от выбора предложенной авторами стратегии
№ п/п	Неравенства произведений интенсивностей	Стратегия	Остаток БСрМ∞(t) у стороны A	Остаток БСр N1(t), N2(t) у стороны В	Результат ГБ
1	2	3	4	5	6
Влияние выбора стратегии на результат БД
Исходные данные для 1a-1в: М=33; µ1=0.09; µ1=0.1; N1=19; λ1=0.11; N2=10; λ2=0.13
1a	λ1µ1<λ2µ2	S{A; B1, B2}	M∞=0	N1(t2)=0, N2(t2)=5	Сторона побеждает при опт. стратегии (1б), проигрывает при стратегии (1а)
1б	λ1µ1<λ2µ2	S{A; B2, B1}	M∞=10→max	N1(t2)=0, N2(t2)=0
1в	λ1µ1<λ2µ2	S{A; B1∪B2}	M∞=6	N1(t1)=0, N2(t1)=0
Влияние выбора стратегии при поражении стороны А на результат БД при λ1µ1<λ2µ
Исходные данные для 2а-2в: М=30; µ1=0.09; µ1=0.1; N1=19; λ1=0.11; N2=10; λ2=0.1
2а	λ1µ1<λ2µ2	S{A; B2, B1}	M∞(t2)=0	N2(t1)=9, N1(t2)=0	Победа стороны В. Оптимальная стратегия (2а) уменьшает остаток БСр у стороны В
2б	λ1µ1<λ2µ2	S{A; B1, B2}	M∞(t2)=0	N1(t1)=3, N2(t1)=10
2в	λ1µ1<λ2µ2	S{A; B1∩B2}, r1=0.5	M∞(t2)=0	N1(t1)=8, N2(t1)=2

Дифференциальные уравнения одноэтапных групповых БД при отсутствии информации о координатах БСр у обеих сторон. Динамика таких действий «по площадям» описывается следующими дифференциальными уравнениями:

Начальными условиями для их решения служат величины:

В случае победы стороны A ее остаток БСр M_∞ определяется уравнением

в котором

В случае победы стороны В ее остаток БСр N_∞ выражается уравнением

где b₁ и b₂ определяются из формулы (7a).

Коэффициент боевого превосходства стороны А при одноэтапных БД вычисляется согласно уравнению

где r₁₂=r₁/r₂; µ₁₂=µ₁/µ₂. В случае победы стороны A К_п(R) должен быть больше 1, при поражении - меньше единицы, при паритете боевых сил и средств - равен единице.

Несмотря на очевидный эффект при выборе оптимальной стратегии, существуют ситуации на ограничение их применения. К ним относятся следующие ситуации:

1 отсутствие влияния выбора стратегии на исход ГБД:

1.1 при наличии разведки и отсутствии доминирующего произведения интенсивностей огневого поражения (строка 1, таблица 2), когда

λ₁µ₁=λ₂µ₂,

при любом выборе стратегии остаток БСр одинаков и составляет M_∞=16 (см. столбцы 9-11,12 таблицы 2);

1.2 при наличии разведки R и явного, превалирующего превосходства (К_п(R)>>1 или К_п(R)<<1) одной из сторон А или В выбор стратегии почти не влияет (строки 3, 5, столбцы 9-11, 12) на исход БД (работает правило: «сила есть - ума для выбора стратегии не надо»);

2 влияние разведки R на выбор стратегии в ГБД:

2.1 при наличии разведки R о координатах БСр у сторон и независимо от коэффициентов превосходства К_п(R)>1 (строка 6 таблицы 2) или К_п(R)<1 (строка 2а таблицы 1) превалирующей является стратегия S{A; B₂, B₁}, определяемая доминирующим произведением интенсивностей поражающего огня сторон

;

2.2 отсутствие разведки всегда снижает эффективность ГБД, см. строки 1 и 2 таблицы 2;

2.3 отсутствие разведки приводит не только к снижению эффективности ГБД, но и к смене самой стратегии S{A; B₁∩B₂} по сравнению с наличием разведки S{A; B₂, B₁}. В этом нетрудно убедиться, сравнив строки 1 и 2, 3 и 4, столбцы 9-11, 12.

2.4 отсутствие разведки даже при паритете сторон все равно приводит к оптимальной стратегии S{A; B₁∩B₂} (строка 8, столбцы 9, 12). В случае отклонения от нее остаток сил у противника значительно возрастает (строка 8, столбцы 10, 11, 12);

2.5 в отличие от боевых действий с однородными группировками, при которых коэффициент боевого противоборства К_п всегда одинаков [1-4], при БД с разнородными - разный и зависит от выбора стратегии, что приводит к разным исходам БД (таблица 2, столбцы 9-12).

Таблица 2
Влияние разведки на выбор стратегии в ГБД
Исходные данные БСр	Результаты ГБД сторон
№	M	µ1	µ2	N1	λ1	N2	λ2	S{A; B1∩B2}	S{A; B1, B2}	S{A; B2, В1}	Примечание
1	2	3	4	5	6	7	8	9	10	11	12
1р	33	0.11	0.1	19	0.1	10	0.11	M∞=16	M∞=16	M∞=16	Безразличие к S
2ор	33	0.11	0.1	19	0.1	10	0.11	M∞=8	M∞=10	N∞=18	S{A; B1∩B2}
3р	66	0.09	0.1	19	0.11	10	0.13	M∞=57	M∞=57	M∞=58	Безразличие к S
4ор	66	0.09	0.1	19	0.11	10	0.13	M∞=50	M∞=34	M∞=31	S{A; B1∩B2}
5р	33	0.09	0.1	40	0.11	30	0.13	N∞=63	N∞=64	N∞=63	Безразличие к S
6р	33	0.09	0.1	19	0.11	10	0.13	M∞=6	N∞=5	М=10	S{A; B2, B1}
7ор	33	0.09	0.1	19	0.11	10	0.13	M∞=1	N∞=12	N∞=19	S{A; B1∩B2}
8ор	33	0.086	0.1	19	0.11	10	0.13	M∞=N∞=0	N∞=12	N∞=20	S{A; B1∩B2}
Примечание: В 1-м столбце буква «р» означает наличие разведки у сторон; буквы «ор» - отсутствие разведки у сторон о координатах БСр.

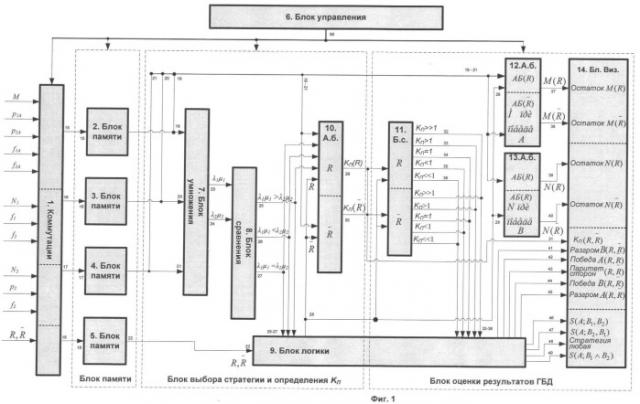
Устройство, реализующее способ, изображенное на рис.1, содержит следующие блоки: коммутатор 1, четыре блока 2, 3, 4, 5 памяти, блок 6 управления, блок 7 умножения, два блока 8, 11 сравнения, блок 9 логики, три арифметических блока 10, 12, 13 и блок 14 визуализации, при этом выходы 15, 16, 17, 18 коммутатора 1 подключены к соответствующим информативным входам 15, 16, 17, 18 блоков 2, 3, 4, 5 памяти, соединенных своими выходами 19, 20, 21 со входами всех 19, 20, 21 арифметических блоков 10, 12, 13 и блока 7 умножения, соединенного своими выходами 23, 24 с соответствующими входами 23, 24 первого блока 8 сравнения, соединенного своими выходами 25, 26, 27 со входами 25, 26, 27 первого арифметического блока и с соответствующими входами 25, 26, 27 блока 9 логики, вход 22 которого связан с выходом 22 блока 5 памяти, а выходом 28 со входами 28 всех арифметических блоков 10, 12, 13, выходы 29, 30 первого арифметического блока 10 соединены со входом 31 блока 9 логики и со входами 29, 30 второго блока 11 сравнения, все выходы 32-36 которого подключены ко входам 32-36 блока 9 логики, выходы 46-49 которого подсоединены ко входам 46-49 блока 14 визуализации, другие входы 37-45 которого подключены к соответствующим выходам 37-45 второго и третьего арифметических блоков 12, 13, управляющие выходы 50 блока 6 управления подключены к управляющим входам 50 всех блоков 1-14.

Работа устройства происходит следующим образом.

Согласно рис.1 исходные данные о наличии R или отсутствии разведданных о координатах БСр сторон А и В, а также характеристики БСр стороны А: М, р_1А, р_2А, f_1A, f_2A и группировок В₁: N₁, p₁, f₁ и В₂: N₂, р₂, f₂ поступают на входы коммутатора 1, а затем по управляющему сигналу с блока 6 управления исходные данные БСр сторон подаются на входы 15, 16, 17, 18 блоков памяти. Значения р_1А, р_2А, f_1A, f_2A, р₁, f₁, p₂, f_2A 2 с выходов 19, 20, 21 блоков памяти в соответствии с рис.1 поступают на входы 19, 20, 21 блока 7 умножения, а с выхода 22 сигнал о наличии R или отсутствии R разведки у сторон на такой же вход 22 блока 9 логики, который своим выходом 28 включает части арифметических блоков 10, 12, 13, выходы которых зависят от наличия R информации о координатах БСр сторон К_п(R), M(R), N(R).

Значения произведений λ₁µ₁, λ₂µ₂ огневого поражения стороны А с каждой из группировок B₁, В₂ с выходов 23, 24 блока 7 умножения приходят на входы 23, 24 первого блока 8 сравнения.

Один из результатов сравнения: λ₁µ₁>λ₂µ₂ или λ₁µ₁<λ₂µ₂ или λ₁µ₁=λ₂µ₂ с одного из выходов 25, 26, 27 блока 8 сравнения идет на один из входов 25, 26, 27 блока 9 логики и на один из входов 25, 26, 27 первого арифметического блока 10. С блока 9 логики с одного из его выходов 46, 47, 48 передается сигнал на соответствующий вход 46, 47, 48 блока 14 визуализации. На блоке 14 визуализации в зависимости от результатов сравнения возникает соответствующая информация о рациональной стратегии ГБД:

при λ₁µ₁>λ₂µ₂ - «Наличие разведки. Стратегия S(A; B₁, B₂)» (вх.46 блока 14);

при λ₁µ₁<λ₂µ₂ - «Наличие разведки. Стратегия S(A; B₂, B₁)» (вх.47 блока 14);

при λ₁µ₁=λ₂µ₂ - «Наличие разведки. Стратегия любая (вх.48 блока 14).

С выхода 28 блока 9 логики разрешающие сигналы R (наличие разведки у сторон А, В о координатах БСр) поступают на входы 28 всех арифметических блоков 10, 12, 13 и вход 28 второго блока 10 сравнения. В первом арифметическом блоке 10 вычисляется величина коэффициента боевого превосходства по формулам (4а), (4б), значение которого поступает на вход 31 блока визуализации.

Также величина К_п(R) поступает на вход 29 блока сравнения. Результат сравнения может быть: К_п(R)>>1; К_п(R)>1; К_п(R)=1; К_п(R)<1; К_п(R)<<1. Согласно результатам сравнения на одном из выходов 32-36 блока 11 появляется сигнал, который поступает на соответствующий вход 32-36 блока 9 логики, с одного из выходов 41-45 которого он передается на один из входов 41-45 блока 14 визуализации. На блоке 14 визуализации кроме значения К_п(R) коэффициента боевого превосходства одной из сторон в зависимости от результатов сравнения возникает соответствующая информация о прогнозировании результатов БД:

при К_п(R)>>1 - «Наличие разведки. Разгром группировок B₁,B₂)» (вх.41 блока 14);

при К_п(R)>1 - «Наличие разведки. Победа стороны А» (вх.42 блока 14);

при К_п(R)=1 - «Наличие разведки. Паритет в БД. (вх.43 блока 14);

при K_п(R)<1 - «Наличие разведки. Победа стороны В» (вх.44 блока 14);

при К_п(R)<<1 - «Наличие разведки. Разгром стороны А» (вх.45 блока 14).

Для случаев, когда К_п(R)>>1 или К_п(R)>1 или К_п(R)=1, сигнал с выхода 28 блока логики подается на вход 28 арифметического блока 12, в котором происходит вычисление в зависимости от выбранной стратегии по одной из формул (3а) или (3б) величины M_∞(A; B₁, B₂) оставшихся БСр стороны A или M_∞(A; B₂, B₁). Величина M_∞(R) подается с выхода 37 на вход 37 блока 14 визуализации.

В случае поражения стороны A, когда К_п<1 или К_п(R)<<1 (разгром стороны А), нанесенный ущерб стороне В определяется сигналом с выхода 28 блока 9 логики, передаваемым на вход 28 арифметического блока 13, в котором происходит вычисление в зависимости от выбранной стратегии согласно формулам (5а) или (5б) величины оставшихся БСр стороны B N_∞(A; B₁, B₂) или N_∞(А; В₂, В₁). Результат N_∞(R) с выхода 39 арифметического блока 13 поступает на вход 39 блока 14 визуализации, на котором появляется информация: «Остаток N_∞(R)=…».

Работа предлагаемого изобретения при отсутствии координат о БСр сторон отличается мало от прежнего описания.

Во-первых, с выхода 22 блока 5 памяти сигнал поступает на вход 22 блока 9 логики, один из выходов 49 которого соединен со входом 49 блока 9 визуализации, на котором высвечивается информация: «Одноэтапные ГБД, S{A; B₁∪B₂}». С выхода 28 блока 9 логики подается сигнал на входы 28 всех арифметических блоков 10, 12, 13. Осуществляется вычисление по формуле (7в) в блоке 10, величина которого с выхода 30 (выход 29 блока 10 не работает) подается на вход 31 блока 14 визуализации. На блоке 14 происходит высвечивание значения .

Значение с выхода 30 также подается на вход 30 второго блока 11 сравнения. Согласно результатам сравнения на одном из выходов 32-36 блока 11 появляется сигнал, который поступает на соответствующий вход 36-36 блока 9 логики, с одного из выходов 41-45 которого он передается на один из входов 41-45 блока 14 визуализации. На блоке 14 визуализации кроме значения коэффициента боевого превосходства одной из сторон в зависимости от результатов сравнения возникает соответствующая информация о прогнозировании результатов БД:

при - «Разведки нет. Разгром группировок B₁, B₂)» (вх.41 блока 14);

при - «Разведки нет. Победа стороны A» (вх.42 блока 14);

при - «Разведки нет. Паритет в БД. (вх.43 блока 14);

при - «Разведки нет. Победа стороны B» (вх.44 блока 14);

при - «Разведки нет. Разгром стороны A» (вх.45 блока 14).

Для ситуаций, когда или или , сигнал с выхода 28 блока логики подается на вход 28 арифметического блока 12, в котором происходит вычисление по формуле (7) величины оставшихся БСр стороны А. Величина подается с выхода 38 на вход 38 блока 14 визуализации, на котором появляется информация: «Остаток БСр ».

В случае поражения стороны А, когда или (разгром стороны А), нанесенный ущерб стороне В определяется сигналом с выхода 28 блока 9 логики, передаваемого на вход 28 арифметического блока 13, в котором происходит вычисление согласно формуле (7б) величины оставшихся БСр стороны В . Результат с выхода 39 арифметического блока 13 поступает на вход 39 блока 14 визуализации, на котором появляется информация: «Остаток БСр ».

Синхронизация работы блоков осуществляется с помощью блока 6 управления.

Реализация предложенного устройства на первом этапе возможна в виде аппаратно-программного комплекса на ПЭВМ, а на втором - в виде автономного устройства.

Источники информации

1. Жиров А.Ю. Военно-прикладная математика. Вероятностные основы оценки эффективности боевых и обеспечивающих действий авиации. - Монино: ВВА им. Ю.А.Гагарина, 2004. С.80-118.

2. Иванов П.И. и др. Основы и применение методов прикладной математики в военном деле. - Монино: ВВА им. Ю.А.Гагарина, 1991. С.186-224.

3. Вентцель Е.С. Введение в исследование операций. М.: Сов. Радио, 1964, 391 с.

4. Абчук В.А., Матвейчук Ф.А., Томашевский Л.П. Уравнения динамики боя / Справочник по исследованию операций. - Москва: Военное изд-во министерства Обороны СССР, 1979, с.322-325.

5. Черноскутов А.И., Климов С.М. и др. Способ и устройство целераспределения по групповым объектам. Решение о выдаче патента на изобретение от 25.08.10 г., G06F 17/00, G0F 5/04, F41G 7/34, F41G 7/00.

6. Пархоменко О.Л. (RU) и др. Аппаратура приема и реализации целеуказания, патент №2236666, F41G 7/00.

7. Даниленко А.И. (RU) и др. Многопозиционная система определения местоположения объектов, патент №2073380, G01S 5/00.

8. Космическая автоматизированная система контроля за подвижными объектами. (RU), патент №2284550, G01S 13/06.

9. Беляев Б.Г. (RU) и др. Способ обнаружения групповых объектов, патент №2157550, G01S 5/00.

1. Способ выбора стратегии целераспределения по групповым объектам, заключающийся в том, что данные своих боевых средств и средств каждой группировки противника записывают в блок памяти, данные передают на входы всех арифметических блоков, отличающийся тем, что в блок памяти записывают наличие или отсутствие информации о координатах боевых средств сторон, которая поступает в блок логики, информацию о количественных и качественных характеристиках всех боевых средств передают на входы блока умножения, с выхода которого произведения интенсивности поражающего огня стороны А на интенсивность каждой из группировок противника сравнивают в первом блоке сравнения с таким же произведением интенсивности поражающего огня стороны А с другой из группировок противника, результаты сравнения поступают на блок визуализации, считывание с которого определяет стратегию ведения боевых действий, величину критерия противоборства вычисляют в первом арифметическом блоке, сравнивают ее во втором блоке сравнения с пороговыми значениями, результаты сравнения подают на блок визуализации, считывание которых определяет исход боевых действий, остатки своих боевых средств или средств противника вычисляют соответственно во втором и третьем арифметическом блоке и осуществляют их считывание с блока визуализации, при отсутствии информации о координатах боевых средств сторон рациональной стратегией будут одноэтапные боевые действия, считываемые с блока визуализации, величину критерия противоборства вычисляют в первом арифметическом блоке, сравнивают ее во втором блоке сравнения с пороговыми значениями, результаты сравнения подают на блок визуализации, считывание которых определяет исход боевых действий, остатки своих боевых средств или средств противника вычисляют соответственно во втором и третьем арифметическом блоках и осуществляют их считывание с блока визуализации.

2. Устройство для реализации способа по п.1, содержащее коммутатор и три блока памяти, блок управления, два блока сравнения, три арифметических блока и блок визуализации, отличающееся тем, что в его состав введены четвертый блок памяти, блок умножения и блок логики, при этом выходы коммутатора подключены к информативным входам всех блоков памяти, соединенных всеми своими первыми тремя выходами с первыми входами всех арифметических блоков и со входами блока умножения, подключенного своими выходами ко входам первого блока сравнения, соединенного своими выходами со вторыми входами первого арифметического блока, подключенного своими выходами к блоку визуализации и к первым входам второго блока сравнения, выходы которого соединены с третьими входами блока логики, первый вход которого подключен к выходу четвертого блока памяти, а второй соединен с выходами первого блока сравнения, первый выход блока логики подключен к третьим входам первого арифметического блока и ко вторым входам второго блока сравнения и вторым входам второго и третьего арифметических блоков, выходы которых соединены с входами блока визуализации, вторая и третья группа выходов блока логики подключены ко входам блока визуализации, управляющие выходы блока управления соединены с управляющими входами всех блоков.