Способ шифрования адаптивным методом многоалфавитной замены

Способ шифрования адаптивным методом многоалфавитной замены

Иллюстрации

Показать все

Реферат

Изобретение относится к области телекоммуникаций и предназначено для защиты передаваемой секретной информации.

Известен способ шифрования методом одноалфавитной замены, который сводится к формированию таблицы замены, в которой каждому символу открытого текста соответствует один символ криптограммы [1]. В качестве примеров таких шифров можно назвать: шифр атбаш, шифр Цезаря, квадрат Полибия. Криптоанализ длинных текстов, зашифрованных методами одноалфавитной замены, не представляет труда. Взлом осуществляют с использованием таблиц частот, либо с помощью алгоритма Т.Якобсена [6].

Известен способ шифрования методом многоалфавитной замены, заключающийся в формировании таблицы многоалфавитной замены, которая используется для замены символов открытого текста на символы криптограммы в зависимости от значения ключа [2]. Данный способ шифрования известен под названием «шифр Виженера». Существует метод взлома этого шифра, который сводится к определению длины использованного ключа (тест Казиски) и последующему частотному анализу криптограммы (вычисление взаимного индекса совпадений) [2].

Наиболее близким из аналогов (прототипом) является техническое решение, описанное в [3].

Известен способ вероятностного многоалфавитного шифрования [3], который сводится к формированию таблицы многоалфавитной замены, в которой число символов замены устанавливается пропорциональным частоте появления исходного символа в открытом тексте. Другими словами: чем чаще появляется символ в открытом тексте, тем большее число символов ему соответствует в таблице замен. Такие шифры получили название гомофонических шифров [3]. Возможно, что такие шифры впервые были исследованы известным математиком Карлом Гауссом. Эти шифры направлены на создание равномерного распределения зашифрованной информации. Однако в них не предусмотрены специальные меры контроля за выходным распределением и это является недостатком гомофонических шифров. Выходное распределение частично сохраняет свойство входного распределения символов открытого текста.

Для подтверждения существования этого недостатка был проведен вычислительный эксперимент, который сводился к тому, что с помощью гомофонического шифра многократно шифровались одинаковые буквы [4].

На фиг.1 показаны гистограммы, полученные при шифровании трехсот букв «А» (фиг.1,а) и трехсот букв «Г» (фиг.1,б) многоалфавитным шифром [4]. Из рисунка видно, что распределения для двух букв существенно различаются (у них различные математические ожидания и дисперсии). Это дает зацепку для успешного криптоанализа.

Техническим результатом данного изобретения является повышение криптостойкости. Изобретение позволяет создать в криптограмме практически равновероятную смесь вещественных чисел. Криптоанализ осложняется полным отсутствием в шифровке следов входного распределения символов открытого текста.

Сущность предлагаемого способа шифрования адаптивным методом многоалфавитной замены, заключается в том, что формируют таблицу многоалфавитной замены, при шифровании каждый символ открытого текста по случайному закону заменяют допустимым вещественным числом из таблицы многоалфавитной замены, полученное в результате замены с помощью таблицы многоалфавитной замены число представляют значением определенного интеграла и в линию связи передают значения верхнего и нижнего пределов интегрирования, причем вид подынтегральной функции и форма таблицы многоалфавитной замены считаются секретными, в процессе передачи шифрограммы производят анализ получающегося распределения вещественных чисел криптограммы и корректируют имеющееся распределение таким образом, чтобы приблизить его к равномерному распределению, для этого перед шифрованием очередного символа открытого текста анализируют гистограмму выходного распределения и находят на гистограмме область глобального минимума, выбирают один из пределов интегрирования таким образом, чтобы он попал в область глобального минимума, а второй предел интегрирования вычисляют с учетом найденного первого предела интегрирования и числа, полученного с помощью таблицы многоалфавитной замены, и при этом среди всех допустимых значений второго предела интегрирования выбирают то значение, которое попадет в зону глобального или локального минимумов гистограммы.

Основная идея заявляемого технического решения заключается в формировании криптограммы в виде равномерной (равновероятной) смеси вещественных чисел.

Равномерность распределения вещественных чисел в криптограмме достигается тем, что в процессе шифрования ведется анализ получающегося (текущего) распределения чисел шифрограммы. С этой целью непрерывно строится гистограмма распределения. При этом очередные элементы шифровки формируются таким образом, чтобы они попали в те места выходного распределения, где наблюдаются провалы (впадины). Возможность изменения (варьирования) положения очередного элемента криптограммы на числовой оси имеется благодаря тому, что при шифровании используются многоалфавитная замена, а также интегральное преобразование числа, полученного в результате многоалфавитной замены.

Алгоритм шифрования таков, что осуществляется непрерывный анализ выходного распределения и выполняется такая коррекция (адаптация) шифра, чтобы обеспечить приближение формируемых чисел к равномерному распределению.

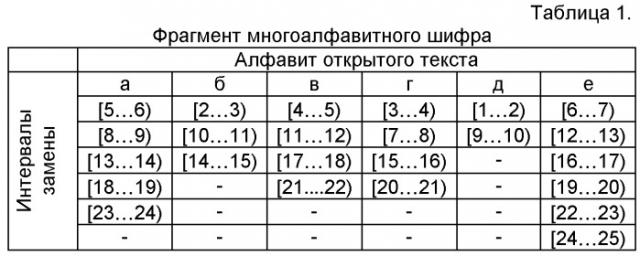
Многоалфавитное шифрование предполагает, что каждый символ открытого текста многократно встречается в таблице замен на различных участках числовой оси. В таблице 1 приведен фрагмент некоторой упрощенной таблицы многоалфавитной замены (ТМЗ). При этом считается, что буква «е» встречается в открытом тексте чаще других, а буква «д» - реже других. По этой причине для буквы «е» выделено 6 интервалов многоалфавитной замены, а для буквы «д» - только 2.

Рассмотрим, как осуществляется шифрование с помощью таблицы многоалфавитной замены. Предположим, что нужно зашифровать фразу «где абба». Шифровку можно создать бесконечным числом способов. При этом каждую букву допустимо заменять любым вещественным числом из указанных интервалов. Приведем две криптограммы для указанной фразы:

1) 15,33-9,101-22,99-18,06-14,57-2,331-5,064

2) 7,105-1,102-12,98-8,473-10,16-14,91-23,26

В предлагаемом шифре после многоалфавитной замены осуществляется интегральное преобразование полученного числа. В результате такого преобразования в линию передается не само число (сформированное с помощью ТМЗ), а два числа, которые при подстановке в определенный интеграл дают это число. Это позволяет один из пределов интегрирования выбирать по случайному закону. При этом нужно находить очередной предел интегрирования таким образом, чтобы формируемое число криптограммы попало в зону наибольшего провала (в зону глобальной впадины) на гистограмме.

При шифровании адаптивным (подстраиваемым) шифром необходимо постоянно решать обратную задачу шифрования: по найденному числу в выходном распределении (находящегося в зоне глобальной впадины) выбирать такое значение предела интегрирования, которое обязательно попадет в заданный интервал гистограммы. Фиг.2 иллюстрирует эту идею. После зашифрования очередного символа гистограмма достраивается (пополняется). На гистограмме выделяется максимальное значение (пик), минимальное значение (глобальная впадина) и провалы (локальные впадины). Формирование криптограммы ведется таким образом, чтобы максимально выровнять имеющееся выходное распределение.

Шифр называется адаптивным по той причине, что элементы выходного распределения подбираются так, чтобы оно в наибольшей степени приближалось (приспосабливались, адаптировались) к равномерному распределению.

Предположим, что наибольший провал на гистограмме наблюдается в интервале чисел [c_i,c_i+1]. Пусть при этом для интегрального преобразования используется некоторая подынтегральная функция f(x)

Для того чтобы уменьшить глубину глобальной впадины, генерируется случайное число а из интервала [c_i,c_i+1]. По таблице многоалфавитной замены определяется значение интеграла I, которое соответствует шифруемому символу. По известному значению нижнего предела интегрирования а и величине интеграла I, находят значение верхнего предела интегрирования b:

b=φ(а, I)

Полученные числа а и b передают в линию. Эти числа являются элементами криптограммы (шифровкой). Заметим, что пределы интегрирования можно формировать и в обратном порядке: сначала выбирать b, а потом вычислять а.

На приемной стороне известны вид использованного интегрального преобразования (подынтегральная функция) и конфигурация таблицы многоалфавитной замены. Эти два элемента являются секретным сеансовым ключом. На приемной стороне они известны, поэтому процесс расшифрования криптограммы не вызывает затруднений. Он сводится к вычислению определенного интеграла по известным значениям нижнего и верхнего пределов интегрирования и определению принятого символа по таблице многоалфавитной замены.

Таким образом, сформированная величина а обязательно попадет в зону наибольшего провала гистограммы, а верхний предел интегрирования b случайно окажется в одной из зон гистограммы.

Величину b также можно приблизить к одной из локальных впадин на гистограмме (эта величина даже может попасть в зону глобальной впадины). Для этого нужно произвести расчеты верхнего предела интегрирования b при имеющемся значении нижнего предела интегрирования а, поочередно выбирая допустимые значения интеграла I из таблицы многоалфавитной замены. При расчете верхнего предела интегрирования b желательно не допустить попадание этого числа в зону пика гистограммы. Все другие результаты расчетов являются приемлемыми. Однако наилучшим вариантом будет попадание вычисленного значения в зону локального или даже глобального минимума.

В предлагаемом способе шифрования каждый символ (буква, знак препинания, цифра) заменяется двумя вещественными числами. Эти два числа являются верхним и нижним пределами определенного интеграла. Значение интеграла используется для того, чтобы на приемной стороне по таблице замен определить, какому символу открытого текста соответствует вычисленное значение интеграла. Предполагается, что вид подынтегральной функции и конфигурация таблицы замен известны только доверенным лицам на передающей и приемной сторонах. В каждом сеансе связи таблица замен и подынтегральная функция определяются секретным ключом.

В следующей таблице приведены соотношения между интегралом и пределами интегрирования для некоторых подынтегральных функций.

Таблица 2.
Соотношения между значениями интеграла и пределами интегрирования
Подынт. функция f(x)	Вычисление нижнего предела а по известным I и b	Ограничения по b	Вычисление верхнего предела b по известным I и а	Ограничения по a
х		b2-2·I≥0		2·I+a 2≥0
x2		-		-
x3		b4-4·I≥0		4·I+a 4≥0
x4		-		-
sinx	а=arc cos(cos b+I)		b=arc cos(cos a-I)
1/х		b>0		a>0
Cx	a=logc(Cb-I·lnC)	Cb>I·lnC	b=logC(I·lnC+Ca)	I·lnC+Ca>0
ex	а=ln(eb-I)	eb>I	b=ln(ea+I)	I>-ea

Осуществление изобретения

Оценим необходимое число интервалов (столбцов) на гистограмме выходного распределения.

Число интервалов k на гистограмме, предназначенной для контроля выходного распределения, можно оценить по формуле Стержесса [5]

где n - число элементов (вещественных чисел) в криптограмме.

Таблица 3 позволяет наглядно представить оценку числа интервалов k в гистограмме в зависимости от длины (числа символов) зашифрованного текста n.

Таблица 3.
Зависимость числа интервалов от числа символов
n	100	1000	10000	100000	1000000
k	7,64	10,96	14,28	17,6	20,92

С учетом того, что при шифровании каждый символ открытого текста s заменяется двумя вещественными числами (n=2·s), то при длине открытого текста (сообщения) s=500 символов число интервалов k на гистограмме оценивается числом 10,96.

Порядок формирования таблицы многоалфавитной замены

Таблица многоалфавитной замены служит на передающей стороне для замены символа открытого текста на некоторое вещественное число. Это число эквивалентно значению определенного интеграла, для которого определяются значения верхнего и нижнего пределов интегрирования. На приемной стороне таблица многоалфавитной замены используется для определения значения принятого символа по величине определенного интеграла, вычисленного с помощью полученных значений верхнего и нижнего пределов интегрирования. Таблица является элементом секретного ключа.

Рассмотрим порядок формирования таблицы многоалфавитной замены.

1. Вначале нужно задаться длиной открытого текста, подлежащего шифрованию. Пусть s_max=50000 символов. Тогда число вещественных чисел, из которых будет состоять криптограмма, n=100000.

2. По формуле (1) следует оценить число необходимых интервалов на гистограмме. Для выбранного значения s_max число интервалов k=17,6.

3. Определить общее число интервалов в таблице многоалфавитной замены t, которое должно быть на один - два порядка больше числа k. Кроме того, число интервалов в ТМЗ должно быть в 3…4 раза больше числа символов в алфавите открытого текста. Таким образом, число интервалов в таблице многоалфавитной замены лежит в пределах 176…1760. Примем t=1000.

4. Найти сумму нормированных частот символов открытого текста

Здесь r - число символов в алфавите открытого текста (r=256 при использовании всех символов таблицы СР-1251 и r=33 при использовании только русских строчных или заглавных букв); g_i - нормированная частота.

Нормированные частоты появления символов в открытом тексте g_i получают путем деления абсолютных частот на наименьшее значение абсолютной частоты.

5. Вычислить число интервалов замен для каждого i-го символа алфавита открытого текста:

Для примера вычислим число интервалов замен для букв «а» и «б»:

6. Задать диапазон (ширину) гистограммы и ее положение на числовой оси. Это означает, что задаются значения a _min и b_max (это для случаев, когда определенный интеграл принимает только положительные значения). Задать ширину и положение на числовой оси таблицы многоалфавитной замены, то есть определить значения I_min и I_max. Перечисленные величины связаны между собой и соотношения между ними зависят от вида подынтегральной функции I_max=φ(a _min,b_max), a I_min≈0.

Например, для подынтегральной функции f(х)=х⁴ правая граница для таблицы многоалфавитной замены вычисляется по формуле

Вычислить ширину одного интервала замен

Пусть Δ=0,1.

7. Составить таблицу многоалфавитной замены, в которой ширина каждого интервала замен равна Δ, а общее число интервалов замен равно t. Все интервалы замен образуют непрерывный интервал чисел шириной Δ·t. Для рассматриваемого случая Δ·t=0,1·1000=100. Каждому интервалу замен ставят в соответствие один из символов алфавита открытого текста. При этом число интервалов замен для буквы «а» равно t_a, для буквы «б» равно t_б и т.д. Интервалы замен для каждого символа располагаются на числовой оси в случайном порядке.

Конфигурация таблицы многоалфавитной замены является одним из элементов секретного ключа. Вторым элементом ключа является вид подынтегральной функции.

Примеры шифрования с помощью адаптивного многоалфавитного шифра

Пример 1.

Предположим, что в текущий момент времени необходимо зашифровать букву «в». В качестве первого ключевого элемента используется таблица 1. Вторым элементом секретного ключа является вид подынтегральной функции. Пусть

f(x)=x⁴.

Предположим, что на гистограмме, составленной на предыдущих шагах шифрования, наблюдается глобальная впадина в диапазоне чисел [6…10).

Для зашифрования буквы «в» по случайному закону из таблицы 1 выбирается один из четырех интервалов замен. Допустим, что выбран интервал 3, то есть (17…18]. Из этого интервала генерируется случайное число, например, I=17,58.

Для заполнения провала на гистограмме генерируется случайное число а из интервала [6…10). Пусть а=8,02. С учетом формулы Ньютона-Лейбница для выбранной подынтегральной функции получаем:

Расчет верхнего предела интегрирования дает значение b=8,0242448. Таким образом, оба числа а и b попали в зону глобальной впадины. «Рассеяние» (отличие, отклонение) пределов интегрирования небольшое.

Пример 2.

Используем в качестве исходных данных числа, приведенные в предыдущем примере, но другую подынтегральную функцию

Для этой функции верхний предел интегрирования вычисляется по формуле

b=3,46·10⁸

Приведенные примеры показывают, что при одних видах подынтегральной функции рассеяние чисел малое, а при других большое.

Выбор вида подынтегральной функции

В качестве подынтегральной функции желательно подобрать функцию, у которой с изменением аргумента меняются амплитуда и частота колебаний. График подобной функции приведен на следующем рисунке (фиг.3).

При выборе вида подынтегральной функции f(х) и нахождении первообразной F(x) можно воспользоваться следующими соображениями.

Представим подынтегральную функцию в виде:

Тогда с учетом известного соотношения

F'(x)=f(x)

для подынтегральной функции (2) получим:

F(x)=-cos w(x).

В качестве w(x) можно использовать большой класс функций, например

w(x)=Ax+С sin Bx.

Тогда

f(х)=(А+ВС cos Bx) sin(Ax+С sin Bx).

В этом случае первообразная определяется выражением

F(x)=-cos(Ax+С sin Bx).

Понятно, что первообразная должна быть использована при вычислении нижнего и верхнего пределов интегрирования, которые являются элементами шифра.

Коэффициенты А, В и С можно использовать в качестве элементов ключа рассмотренного шифра. Очевидно, что еще одним элементом ключа является конфигурация ТМЗ.

Оценка числа вариантов формирования таблиц многоалфавитной замены

В данном способе шифрования ключевыми элементами являются таблица многоалфавитной замены и вид подынтегральной функции. Представляет интерес оценка числа различных конфигураций ТМЗ (другими словами: оценка числа ключей).

Пусть имеется алфавит символов открытого текста, состоящий из m символов.

Рассмотрим следующий способ формирования таблицы многоалфавитной замены. Поставим в соответствие каждому символу алфавита открытого текста не менее одного интервала вещественных чисел:

[1,2);[2,3);…;[n-1,n),

причем число интервалов должно быть больше числа символов n>m.

Предположим, что сформирована некоторая ТМЗ, то есть каждому символу открытого текста поставлен в соответствие один или более интервалов ТМЗ. При шифровании символ открытого текста заменяется вещественным числом из допустимого (разрешенного) интервала ТМЗ. Все интервалы ТМЗ на отрезке [1,n] должны быть размещены таким образом, чтобы образовать непрерывную числовую ось (непрерывный интервал). Потребуем также, чтобы любому символу открытого текста не соответствовали никакие два смежных интервала ТМЗ. Другими словами: один и тот же символ не может заменяться числами из соседних (смежных) интервалов ТМЗ.

Обозначим число всевозможных различных способов формирования (конфигураций) ТМЗ символом .

Теорема.

Справедлива рекуррентная формула:

Доказательство.

Пусть число найдено и определены все способы перестановок символов и интервалов (то есть определено число модификаций ТМЗ при данных m и n). Тогда при увеличении числа интервалов на один число модификаций ТМЗ может быть определено следующими двумя взаимно дополняющимися способами.

1. Добавлением для имеющихся n интервалов в ТМЗ дополнительного интервала [n,n+1). Без введенного выше ограничения таких добавлений может быть m штук, так как можно добавить этот интервал в группу промежутков, соответствующих одному из m символов алфавита. Однако по условию задачи нельзя добавлять дополнительный интервал в группу того символа, которому соответствует промежуток [n-1,n), смежный с [n,n+1).

Значит, таких способов будет .

2. Способ получения новой ТМЗ может быть, кроме того, таким:

а) берется ТМЗ, которая описывает способ размещения m-1 символов в n числовых интервалах, удовлетворяющий сформулированным выше условиям (при этом m-й символ в формировании ТМЗ не участвует);

б) размещается оставшийся m-й символ в дополнительном интервале [n,n+1). Таких способов будет (по числу символов).

Все способы получения любой конфигурации ТМЗ исчерпываются возможностями рассмотренных двух способов. Отсюда вытекает формула (3).

Теорема доказана.

Каждому способу соответствует свое слагаемое в формуле (3)

Проиллюстрируем рассмотренную теорему с помощью конкретного простого примера формирования ТМЗ.

Возьмем m=3; n=3. Тогда формула (1) будет иметь вид:

Путем ручного перебора всех возможных перестановок определим величину .

При числе символов в алфавите m=3 и числе интервалов n=3 число перестановок составляет 3!=6.

АБВ

АВБ

БАВ

БВА

ВАБ

ВБА

Итак: .

При увеличении числа интервалов на один (n=4), число перестановок увеличивается вдвое:

АБВА	БВАБ	БАВА
АБВБ	БВАВ	БАВБ
АВБА	ВАБА	ВБАБ
АВБВ	ВАБВ	ВБАВ

Таким образом, первое слагаемое (первый способ) дает 12 перестановок.

Рассмотрим второе слагаемое (4).

Число возможных перестановок для m=2 и n=3 равно двум:

АБА

БАБ

Или

АВА

BAB

ВБВ

БВБ

Таких сочетаний букв не было в предыдущих перестановках, определенных с помощью первого слагаемого.

Итак: число допустимых перестановок для двух символов и трех интервалов .

Введение третьего символа алфавита и четвертого интервала приведет к появлению таких комбинаций:

АБАВ

БАБВ

АВАБ

ВАВБ

БВБА

ВБВА

Таким образом, второе слагаемое дает 6 перестановок.

Подводя итоги ручных расчетов, можно сказать, что ТМЗ для m=3, n=3 состоит из 12+6=18 перестановок (ключей, комбинаций). Расчет с помощью формулы (3) дает такой же результат.

В рамках исследования числа возможных комбинаций (числа разновидностей ТМЗ) была написана программа на языке С# под операционную систему Windows ХР.

В процессе работы пользователь вводит число символов и интервалов в ТМЗ (фиг.4). Если число символов равно числу интервалов, то есть на каждый символ приходится по одному интервалу, то число комбинаций равно факториалу числа символов. Таким образом, для 256 символов (например, кодовая таблица СР-1251) существует 8,5·10⁵⁰⁶ возможных комбинаций. В процессе разработки данной программы возникла трудность, связанная с тем, что максимальное число, которое может быть использовано в языке С#, ограничено величиной 1,7·10³⁰⁸.

Данная проблема была решена реализацией алгоритма расчета числа перестановок в математическом пакете Maple 13. На фиг.5 приведен пример расчета числа комбинаций для 255 символов и 256 интервалов.

При n=256 и m=1000 число комбинаций составляет 1,74·10²⁴⁰⁴.

Проведенные расчеты говорят о большом числе ключей, которые могут быть использованы в этом шифре. Заметим, что расчеты произведены для одной подынтегральной функции. Понятно, что число ключей линейно возрастает с увеличением числа подынтегральных функций.

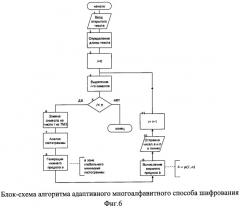
На фиг.6 приведена блок-схема алгоритма, который реализует одну из модификаций предлагаемого способа шифрования.

Реализация рассмотренного способа шифрования была осуществлена с помощью двух вариантов программ Samara_MIM и Samara_BAF, которые были разработаны двумя разными авторами.

Рассмотрим основные возможности первой программы Samara_BAF.

Главная панель управления позволяет выбрать режим работы программы (фиг.7).

Рассмотрим режим шифрования.

В окне «Шифрование» имеется ниспадающее меню, определяющее порядок работы с открытым текстом (фиг.8).

Если нужно использовать текущий открытый текст, то перед выбором соответствующей вкладки в выпадающем меню надо ввести в текстовое поле открытый текст.

После ввода открытого текста, программа Samara_BAF вычисляет статистику открытого текста (фиг.9) и строит гистограмму (фиг.10). Для этого необходимо переключиться на соответствующую вкладку, находящуюся над блоком вывода информации.

Переключившись на вкладку «Установка параметров» (фиг.11) можно изменить вид подынтегральной функции, число замен в таблице многоалфавитной замены и шаг замен в ТМЗ.

Для шифрования нужно нажать на соответствующую кнопку (фиг.12).

Для сохранения результатов надо нажать на одноименную кнопку (фиг.13) и выбрать директорию с заданием имени сохраняемых файлов (расширение файлов при сохранении указывать не нужно).

При расшифровании необходимо указать в программе соответствующий режим работы и импортировать в программу файл с ТМЗ (этот файл имеет расширение ^∗.tmz) и файл с шифрованным сообщением (файл имеет расширение ^∗.mes), нажимая соответствующие кнопки в окне «Дешифрование». Далее следует указать подынтегральную функцию с параметрами и нажать кнопку «Дешифровать». После чего программа выведет в текстовом поле расшифрованное сообщение, которое можно будет сохранить в текстовом файле нажатием на кнопку «Сохранить расшифрованное сообщение». Результаты работы программы в режиме расшифрования показаны на фиг.14.

Рассмотрим основные возможности второй программы (Samara_MIM).

Программа написана на языке С# под операционную систему Windows ХР. Для запуска программы требуется установить пакет Framework.Net версии 3.5.

Пользовательский интерфейс (фиг.15) предоставляет возможность ввода открытого текста, выбора конкретного вида ТМЗ из файла, выбора вида подынтегральной функции и ее коэффициентов. Таблица многоалфавитной замены загружается из выбранного пользователем файла, результаты сохраняются в выбранный файл.

Для каждой буквы открытого текста проводится определение пределов интегрирования, которые передаются на приемную строну, где по известной ТМЗ и подынтегральной функции восстанавливается открытый текст.

Нижний предел интегрирования выбирается случайно среди множества чисел из минимально заполненных интервалов гистограммы. Счетчик чисел, попавших в какой-либо интервал гистограммы, увеличивается на единицу.

Далее производится расчет второго предела интегрирования. При этом, используя все возможные интервалы чисел для шифруемой буквы (в соответствии с ТМЗ) по формуле Ньютона-Лейбница, вычисляются вторые (верхние) пределы интегрирования. Из всех рассчитанных значений верхних пределов интегрирования выбираются те, которые попадают в зоны локального или глобального минимума на гистограмме. Среди них случайным образом выбирается одно число, которое и будет считаться вторым (верхним) пределом интегрирования. Счетчик значений, попавших в выбранный диапазон гистограммы, увеличивается на единицу.

После шифрования всего текста получается итоговая гистограмма.

Был проведен эксперимент по зашифрованию и расшифрованию текстов с помощью разработанных программ. Обмен криптограммами между двумя программами был успешным. Переданные и принятые криптограммы были расшифрованы верно.

Перечислим основные положительные стороны заявляемого технического решения.

Заявляемый способ адаптивного многоалфавитного шифра целесообразно использовать при шифровании объемных текстов. Криптоанализ данного шифра осложнен тем, что элементы криптограммы представляют собой вещественные числа, распределенные практически равномерно.

Способ легко реализуем программным или аппаратным (микросхема) путем.

Для дешифрирования криптограммы на приемной стороне достаточно с помощью формулы Ньютона-Лейбница вычислить определенный интеграл и полученное значение интеграла использовать для определения символа по ТМЗ.

На передающей стороне требуется с помощью ТМЗ заменить символ на число, а над полученным числом выполнить интегральное преобразование, в результате которого получаются значения нижнего и верхнего пределов интегрирования. Имеющаяся свобода в выборе пределов интегрирования позволяет их подбирать таким образом, чтобы получить равномерное распределение чисел криптограммы.

Криптостойкость шифра базируется на сложности решения математической задачи при большом числе неизвестных значений и секретности формы ТМЗ.

Список литературы

1. Алексеев А.П. Информатика 2007. - М.: СОЛОН-ПРЕСС, 2007. - 608 с.

2. Алферов А.П., Зубов А.Ю., Кузьмин А.С., Черемушкин А.В. Основы криптографии. - М.: Гелиос АРВ, 2002. - 480 с.

3. Молдовян А.А., Молдовян Н.А. Советов Б.Я. Криптография. - СПб.: Издательство «Лань», 2001. - 224 с.

4. Алексеев А.П., Орлов В.В. Стеганографические и криптографические методы защиты информации: учебное пособие. - Самара: ИУНЛ ПГУТИ, 2010. - 330 с.

5. Алексеев А.П., Камышенков Г.Е. Использование ЭВМ для математических расчетов. - Самара: Парус, 1998. - 190 с.

6. Аграновский А.В., Хади Р.А. Практическая криптография: алгоритмы и их программирование. - М.: СОЛОН-Пресс, 2009, 256 с.

Способ шифрования адаптивным методом многоалфавитной замены, заключающийся в том, что формируют таблицу многоалфавитной замены, при шифровании каждый символ открытого текста по случайному закону заменяют допустимым вещественным числом из таблицы многоалфавитной замены, отличающийся тем, что полученное в результате замены с помощью таблицы многоалфавитной замены число представляют значением определенного интеграла и в линию связи передают значения верхнего и нижнего пределов интегрирования, причем вид подынтегральной функции и форма таблицы многоалфавитной замены считаются секретными, в процессе передачи шифрограммы производят анализ получающегося распределения вещественных чисел криптограммы и корректируют имеющееся распределение таким образом, чтобы приблизить его к равномерному распределению, для этого перед шифрованием очередного символа открытого текста анализируют гистограмму выходного распределения и находят на гистограмме область глобального минимума, выбирают один из пределов интегрирования таким образом, чтобы он попал в область глобального минимума, а второй предел интегрирования вычисляют с учетом найденного первого предела интегрирования и числа, полученного с помощью таблицы многоалфавитной замены, и при этом среди всех допустимых значений второго предела интегрирования выбирают то значение, которое попадет в зону глобального или локального минимумов гистограммы.