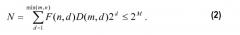Устройство и способ комбинаторного кодирования малой сложности сигналов

Устройство и способ комбинаторного кодирования малой сложности сигналов

Иллюстрации

Показать все

Реферат

Уровень техники

Общеизвестны способы кодирования векторных или матричных величин для речевых сигналов, аудиосигналов, сигналов изображения, видеосигналов и других сигналов. Один такой способ, описанный в патенте США 6236960, Peng et al (который включен в данный документ по ссылке), известен как факториальное импульсное кодирование (или FPC). FPC может кодировать вектор x_i, используя в сумме M битов, с учетом того, что:

и все значения вектора x_i представляют собой целочисленные значения, так что

-m≤x_i≤m, где m представляет собой суммарное количество импульсов единичной амплитуды, и n представляет собой длину вектора. Суммарные M битов используются для кодирования N комбинаций максимально эффективным образом, так что сохраняется справедливость следующего выражения, которое описывает теоретически минимальное количество комбинаций:

Для этого уравнения F(n,d) представляют собой количество комбинаций d ненулевых векторных элементов по n положениям, определяемым посредством:

D(m,d) представляет собой количество комбинаций d ненулевых векторных элементов при заданных m суммарных единичных импульсах, определяемых посредством:

и 2^d представляет комбинации, необходимые для описания полярности (знака) d ненулевых векторных элементов. Член min(m,n) учитывает случай, когда количество импульсов m единичной величины превышает длину n вектора. Способ и устройство кодирования и декодирования векторов этого вида были полностью описаны в известном уровне техники. Кроме того, практическая реализация данного способа кодирования была описана в стандарте C.S0014-B Проекта 2 партнерства по созданию системы третьего поколения (3GPP2), где длина вектора n=54, и количество импульсов единичной величины m=7 создает кодовое слово из M=35 битов.

Хотя эти значения n и m не вызывают какой-либо чрезмерной нагрузки из-за сложности, большие значения могут быстро вызвать проблемы, особенно в мобильных карманных устройствах, в которых необходимо поддерживать объем памяти и сложность вычислений минимально возможными. Например, использование данного способа кодирования для некоторых применений (таких как аудиокодирование) может потребовать n=144 и m=28 или выше. При таких условиях затраты, связанные с выведением комбинаторного выражения F(n,d), используя способы известного уровня техники, могут быть слишком высокие для практической реализации.

Рассматривая эти затраты более подробно, можно переписать уравнение 3 как:

Непосредственная реализация является проблематичной, так как F(144, 28) потребует 197 битов точности в числителе и 98 битов точности в знаменателе для получения 99-битового частного. Так как большинство процессоров цифровой обработки сигналов (DSP), используемых в современных карманных устройствах, обычно поддерживают только операции умножения 16 бит × 16 бит, необходимо применять специальные подпрограммы умножения/деления с многократно увеличенной точностью. Такие подпрограммы требуют последовательности вложенных операций умножения/накопления, которые обычно требуют порядка k операций умножения/накопления (MAC), где k представляет собой количество 16-битовых сегментов в операнде. Для 197-битового операнда . Поэтому выполнение одного 197×16-битового умножения потребует минимум 13 операций MAC плюс операции сдвига и сохранения. Член знаменателя вычисляется подобным образом для получения 98-битового результата. Кроме того, требуется 197/98-битовое деление, которое представляет собой очень сложную операцию, таким образом, вычисление всего факториального отношения в уравнении 5 потребовало бы значительных ресурсов.

В попытке уменьшить сложность уравнение 5 можно переписать для распределения операций деления для получения следующего:

В данном выражении уменьшается динамический диапазон операций деления, но, к сожалению, необходимо повышенное разрешение частного, чтобы точно представить деление на 3, 7, 9 и т.д. Чтобы приспособить эту структуру, также необходима операция округления, чтобы гарантировать целочисленный результат. При заданном большом количестве операций деления с высокой точностью эта реализация не решает надлежащим образом проблему сложности для больших m и n и дополнительно имеет потенциальную возможность получения неправильного результата из-за накопленных ошибок точности.

В еще другой реализации уравнение 5 может быть переупорядочено следующим образом:

Если это выражение оценивается слева направо, то результат всегда создает целочисленное значение. Хотя этот способ контролирует вопрос точности и динамического диапазона в некоторой степени, большие значения m и n все же требуют интенсивного использования операций умножения и деления с многократно увеличенной точностью.

Наконец, чтобы минимизировать сложность вычислений, может быть возможным выполнять предварительное вычисление и сохранение всех факториальных комбинаций в таблице соответствия. Таким образом, все значения F(n,m) могут быть просто сохранены в матрице размера n×m и соответствующим образом извлечены из памяти, используя всего несколько циклов процессора. Проблема с данным подходом, однако, заключается в том, что когда n и m становятся большими, таким же становится связанное с ними требование к памяти. Ссылаясь на предыдущий пример, F(144, 28) потребует 144 × 28 × =52416 байтов памяти, что является чрезмерным для большинства мобильных карманных устройств. Поэтому существует потребность в способе и устройстве для комбинаторного факториального импульсного кодирования малой сложности векторов.

Краткое описание чертежей

Признаки изобретения, которые, как считается, являются новыми, подробно изложены в прилагаемой формуле изобретения. Само изобретение, однако, как в отношении организации, так и способа работы, вместе с его целями и преимуществами, лучше всего может быть понято посредством ссылки на последующее подробное описание изобретения, которое описывает некоторые примерные варианты осуществления изобретения, рассматриваемые вместе с прилагаемыми чертежами, на которых:

фиг.1 представляет собой блок-схему кодера.

Фиг.2 представляет собой блок-схему декодера.

Фиг.3 представляет собой блок-схему последовательности операций, изображающую работу генератора комбинаторной функции по фиг.1 и фиг.3.

Фиг.4 представляет собой блок-схему кодера согласно различным вариантам осуществления.

Фиг.5 представляет собой блок-схему последовательности операций, изображающую работу кодера согласно различным вариантам осуществления.

Фиг.6 представляет собой блок-схему декодера согласно различным вариантам осуществления.

Фиг.7 представляет собой блок-схему последовательности операций, изображающую работу декодера согласно различным вариантам осуществления.

Фиг.8 представляет собой блок-схему последовательности операций, изображающую работу кодера, использующего оценку плотности, согласно различным вариантам осуществления.

Фиг.9 представляет собой блок-схему последовательности операций, изображающую работу декодера, использующего оценку плотности, согласно различным вариантам осуществления.

Фиг.10 представляет собой блок-схему последовательности операций, изображающую работу кодера относительно порогового значения согласно различным вариантам осуществления.

Фиг.11 представляет собой блок-схему последовательности операций, изображающую работу декодера относительно порогового значения согласно различным вариантам осуществления.

Специалист в данной области техники понимает, что элементы на фигурах изображены для простоты и ясности и необязательно, чтобы они были нарисованы в масштабе. Например, размеры некоторых элементов на фигурах могут быть увеличены относительно других элементов, чтобы способствовать улучшению понимания вариантов осуществления настоящего изобретения.

Подробное описание

Хотя данное изобретение допускает наличие варианта осуществления во многих разных видах, на чертежах показаны и в данном документе подробно описываются конкретные варианты осуществления, понимая, что настоящее раскрытие должно рассматриваться как пример принципов изобретения и не предполагается, что оно ограничивает изобретение конкретными изображенными и описанными вариантами осуществления. В описании ниже подобные позиции используются для описания таких же, подобных или соответствующих деталей на нескольких видах чертежей.

В данном документе относительные термины, такие как первый и второй, верхний и нижний и т.п., могут использоваться исключительно для различения одного объекта или действия от другого объекта или действия, не требуя или подразумевая обязательно какой-либо фактической такой зависимости или порядка между такими объектами или действиями. Термины «содержит», «содержащий» или любой другой их вариант, как предполагается, охватывают неисключительное включение, так что процесс, способ, предмет или устройство, которое содержит список элементов, не включает в себя только эти элементы, но может включать в себя другие элементы, не перечисленные в явной форме или присущие такому процессу, способу, предмету или устройству. Элемент, которому предшествует «содержит …» не исключает, без дополнительных ограничений, наличие дополнительных идентичных элементов в процессе, способе, предмете или устройстве, которые содержат элемент.

Ссылка в данном документе на «один вариант осуществления», «некоторые варианты осуществления», «вариант осуществления» или подобные термины означает, что конкретный признак, структура или характеристика, описанные в связи с вариантом осуществления, включен в по меньшей мере один вариант осуществления настоящего изобретения. Таким образом, необязательно, что все появления таких фраз или в различных местах в данном описании изобретения ссылаются на один и тот же вариант осуществления. Кроме того, конкретные признаки, структуры или характеристики могут объединяться без ограничения любым подходящим образом в одном или нескольких вариантах осуществления.

Термин «или», как он используется в данном документе, должен интерпретироваться как включающий или означающий любое одно или любое сочетание. Поэтому «А, В или С» означает «любое из следующего: А; В; С; А и В; А и С; В и С; А, В и С». Исключение для этого определения имеет место только тогда, когда сочетание элементов, функций, этапов или действий является некоторым образом в своей основе взаимно исключающим.

Настоящее изобретение относится, в основном, к кодированию векторов и, в частности, к комбинационному факториальному импульсному кодированию векторов.

Как показано на чертежах, на которых подобные позиции обозначают подобные компоненты, фиг.1 представляет собой блок-схему кодера 100. Кодер 100 содержит генератор 102 векторов, схему (кодер) 106 комбинационного кодирования, генератор 108 комбинационных функций и схему 104 другого кодирования. Во время работы входной сигнал, подлежащий кодированию, принимается генератором 102 векторов. Как известно в технике, входной сигнал может содержать такие сигналы, как речевой сигнал, аудиосигнал, сигнал изображения, видеосигнал и другие сигналы.

Генератор 102 векторов принимает входной сигнал и создает вектор x_i. Генератор 102 векторов может содержать любое количество парадигм кодирования, включая, но не ограничиваясь ими, кодирование речи CELP (линейное предсказание с кодовым возбуждением), описанное Peng et al, кодирование в области преобразования для аудио, изображений и видео, включая способы, основанные на дискретном преобразовании Фурье (DFT), дискретном косинусном преобразовании (DCT) и модифицированном дискретном косинусном преобразовании (MDCT), кодирование с вейвлет-преобразованием, прямую импульсно-кодовую модуляцию (PCM) во временной области, дифференциальную PCM, адаптивную дифференциальную PCM (ADPCM) или любой один из семейства методов полосного кодирования, которые общеизвестны в технике. Фактически, любой вектор сигнала вида, приведенного выше, может быть выгодно обработан согласно некоторым вариантам осуществления настоящего изобретения.

Схема 106 комбинаторного кодирования принимает вектор x_i и использует факториальное импульсное кодирование для получения кодового слова C. Как описано выше, факториальное импульсное кодирование может кодировать вектор x_i, используя в сумме M битов, при условии, что , и все значения вектора x_i являются целочисленными, так что -m≤x_i≤m, где m представляет собой суммарное количество единичных импульсов амплитуды, и n представляет собой длину вектора. Как описано выше, большие значения m и n могут быстро вызывать проблемы, особенно в мобильных карманных устройствах, в которых необходимо поддерживать объем памяти и сложность вычислений максимально низкими.

Чтобы решить этот вопрос, генератор 108 комбинаторных функций использует метод малой сложности для получения F'(n,d). Схема 106 комбинаторного кодирования затем использует F'(n,d) для получения кодового слова C. Схема 108 использует аппроксимации с относительно низким разрешением (биты точности) факториальных комбинаций F'(n,d), которые обеспечивают только необходимую точность для возможности генерирования достоверного кодового слова. Т.е. пока сохраняются некоторые свойства, подходящая аппроксимация функции F(n,d) достаточна для того, чтобы гарантировать, что результирующее кодовое слово является однозначно декодируемым.

Чтобы описать генерирование F'(n,d), сначала выводят функцию F'(n,d), которая представляет собой подходящую аппроксимацию F(n,d). Первым этапом является взятие логарифма по произвольному основанию a в уравнении 5 и взятие антилогарифма по основанию a переупорядоченных членов:

где функция exp_a(k)=a^k. Затем определяют функции P(i), Q(d) и R(k) и подставляют в уравнение 8, так что:

Однако согласно примерному варианту осуществления настоящего изобретения не является необходимым, чтобы F(n,d) и F'(n,d) были эквивалентными по порядку, чтобы результирующее кодовое слово являлось однозначно декодируемым. Существует только два условия, которые достаточны для того, чтобы они были справедливыми:

и

Для первого условия ограничение просто определяет, что если F'(n,d)<F(n,d), тогда будет перекрытие кодовых пространств, и, впоследствии, будет более одного входа, способного генерировать конкретное кодовое слово; таким образом, кодовое слово не является однозначно декодируемым. Второе условие определяет, что «ошибка» для данного n, d должна быть больше или равна сумме слагаемых ошибки, связанных с предыдущим элементом рекурсивной зависимости, описанной у Peng et.al в патенте США 6236960. Может быть показано, что F(n,d)=F(n-1,d)+F(n-1,d-1), которое верно только тогда, когда комбинаторное выражение точно равно F(n,d)=!/d!(n-d)!. Однако, когда неравенство в уравнении 11 является достаточным, оно может необязательно быть верным для всех значений n и d. Для таких значений F(n,d) может удовлетворять другому неравенству, выведенному из уравнения 31 у Peng et al. и определяется:

В данном случае, уравнение 11 должно выполняться со строгим неравенством для некоторых (m,k), (m≤n), (k≤d), т.е.:

Возвращаясь обратно к уравнению 9, изобретатели теперь хотят сгенерировать F'(n,d) посредством создания функций P'(i), Q'(d) и R'(k) с аппроксимацией малой сложности исходных функций, так что:

и где выполняются условия, приведенные в уравнениях 10 и 11. Рассматривая P(i), можно аппроксимировать функцию, так что P'(i)≥log_a(i), . Если выбрать a=2 и затем ограничить P'(i) до 32 битов точности, то легко реализовать результирующие операции на карманном мобильном устройстве, так как большинство DSP поддерживают 32-битовые сложения с одним циклом. Поэтому изобретатели определяют:

где l(i) представляет собой коэффициент сдвига, который может изменяться как функция i. В предпочтительном варианте осуществления l(i)=l=21, но возможны многие другие множества значений. Для данного примера коэффициент 2^l эквивалентен сдвигу l битов влево, посредством чего функция округления до ближайшего меньшего целого удаляет дробные биты, в тоже время округляя до следующего наибольшего целого числа, и, наконец, коэффициент 2^-l сдвигает результаты обратно вправо на l битов. Используя данную методологию, функция P'(i)≥log₂(i) для всех i≥1 и также обеспечивает достаточный динамический диапазон и точность, используя только 32 бита, так как 9 битов положительного целочисленного разрешения в области log₂ могут представлять 512-битовое число. Чтобы избежать сложности вычислений этих значений в реальном времени, они могут вычисляться предварительно и сохраняться в таблице, используя 144 × 4 битов памяти для примера F(144, 28). Используя подобную методологию для аппроксимации Q(d), изобретатели получают:

где функция округления до ближайшего меньшего целого используется из-за вычитания величины из общего. Это гарантирует, что Q'(d), так что вклад Q'(d) будет гарантировать F'(n,d)≥F(n,d). Хотя l(j) может принимать многие значения в зависимости от конфигурации m и n, предпочтительный вариант осуществления использует значение l(j)=l=14 для переменного коэффициента сдвига. Подобно P'(i), Q'(d) может вычисляться предварительно и сохраняться в таблице, используя только 28×4 байтов памяти для примера F(144, 28). Для определения R'(k) необходимо сначала определить k следующим образом:

С P'(i) и Q'(d), определенными выше, k представляет собой предпочтительно 32-битовое число с 8-битовой целочисленной составляющей k_i без знака и 24-битовой дробной составляющей k_f. Используя это, можно вывести R'(k)≥exp₂(k)=2^k, принимая k=k_i+k_f, и затем беря антилогарифм по основанию 2 для получения 2^k=. Затем можно использовать разложение в ряд Тейлора для оценки дробной составляющей до требуемой точности, представленной , округляя результат, используя функцию округления до ближайшего большего целого, и затем сдвигая соответствующим образом результат для формирования результата с многократно увеличенной точностью (только с l старшими битами), так что:

где представляет собой целочисленный коэффициент сдвига, применяемый к результату разложения в ряд Тейлора. В данном случае, l представляет собой коэффициент сдвига, используемый подобно уравнениям 15 и 16, чтобы гарантировать R'(k)≥2^k. Однако, так как R'(k) практически не может быть вычислена предварительно для эффективной работы в реальном времени, необходимо очень внимательно относится к заданию точных операций, необходимых как в кодере, так и в декодере для обеспечения того, чтобы восстановленный вектор сигнала точно соответствовал вектору входного сигнала. Отметьте, что R'(k) может быть получен в результате сдвига влево , который может быть точно представлен l битами.

В вышеприведенном описании функции P'(i), Q'(d) и R'(k) были выбраны так, что каждая индивидуальная оценка функции гарантирует, что результирующее F'(n,d)≥F(n,d). Однако необходимо только, чтобы совокупное влияние удовлетворяло данному условию. Например, P'(i) и Q'(d) могут быть такими, которые описаны выше, но R'(k) может быть более обычной функцией R'(k)≈2^k, которая может обрезать или округлять самые младшие биты, так что R'(k) может быть меньше, чем 2^k для некоторых значений k. Это допустимо, пока данное влияние является незначительным относительно влияния P'(i) и Q'(d), поэтому свойства в уравнениях 10 и 11 все же сохраняются действительными.

Также любая функция P'(i), Q'(d) и R'(k) может использоваться без потери общности, пока выполняются свойства уравнений 10 и 11. Необходимо быть внимательным, однако, что повышение скорости передачи битов может происходить, если используется слишком малая точность. Также необходимо отметить, что существует присущий компромисс между скоростью передачи битов и сложностью, и для больших значений m и n увеличение на 1 или 2 бита может быть приемлемым компромиссом для существенного снижения сложности.

Теперь описывается формулировка частичного кодового слова C для положения и величин в схеме 106 комбинаторного кодирования. Пусть π={p₁, p₂, …, p_v} будут положениями ненулевых импульсов (в возрастающем порядке) и µ={m₁, m₂, …, m_v} величинами в соответствующих положениях у вектора x. Код для положений импульса определяется:

и код для величин импульса определяется:

Таким образом, формулировка этого кодового слова требует сложение v и v-1 чисел с многократно увеличенной точностью. Подобные операции вычитания необходимы в декодере. Эти операции также добавляют сложность способу FPC, когда m и n большие. Рассмотрим кодирование/декодирование аудиосигнала для системы многоуровневого встроенного кодирования. Этот метод используется для кодирования преобразования сигнала остаточной ошибки на трех уровнях многоуровневой системы. Пусть размер 20-мс блока равен n=280 и одинаков для всех уровней. Количество импульсов для кодирования зависит от скорости передачи битов каждого уровня. Если каждый уровень составляет 8 кбит/с, 16 кбит/с или 32 кбит/с, тогда они требуют 160 битов, 320 битов и 640 битов для кодирования 20-мс блока соответственно. Используя метод FPC, блок длиной 280 может кодироваться с использованием 28, 74 и 230 импульсов для 160 битов, 320 битов и 640 битов на уровень соответственно. Операции с многократно увеличенной точностью в уравнениях 19 и 20 выполняются на процессоре цифровой обработки сигналов, который обычно работает с 16-битовыми словами. Таким образом, для образования 160-битового кодового слова операции сложения необходимы для выполнения свыше 10 слов, и для 640-битового кодового слова операция сложения должна выполняться по 40 словам. Каждая операция сложения занимает 4 единицы (генерирование переноса, перемещение в массив, сложение с учетом разряда переноса). Следовательно, кодирование/декодирование k-битового кодового слова на p-уровнях многоуровневой системы требует операций/с. Для различных значений n, m и p сложность операций сложения/вычитания с многократно увеличенной сложностью показана в таблице 1. В этой таблице WMOPS обозначает взвешенный миллион операций в секунду.

Таблица 1 Сложность сложения/вычитания при кодировании/декодировании FPC, используя способ известного уровня техники
Кол-во уровней (p)	Размер блока (n)	Скорость передачи битов уровня/биты на 20-мс блок (k)	Кол-во импульсов (m)	Сложность сложения/вычитания с многократно увеличенной точностью
3	280	8 кбит/c/160	28	0,64 WMOPS
3	280	16 кбит/с/320	74	3,48 WMOPS
3	280	32 кбит/с/640	230	22,0 WMOPS

Из таблицы 1 отмечаем, что, если скорость передачи битов удваивается, сложность сложения с многократно увеличенной точностью повышается в шесть раз.

Как упомянуто выше, комбинаторная функция заменяется аппроксимирующей функцией F'(n,r), которая определяется следующим образом:

где

и R'(k) представляет собой аппроксимацию функции R'(k)≈2^k, заданной как:

где k=k_i+k_f разбивается на целочисленную и дробную составляющие k, и представляет собой разложение в ряд Тейлора с низким разрешением дробной составляющей k. Основываясь на вышеприведенных предварительно определенных функциях Q'(r) и R'(k), сначала получают P'(i), так что однозначно определяемое неравенство декодируемости

выполняется для всех значений n и d.

Возвращаясь обратно к уравнениям 19 и 20, замена аппроксимирующих функций F' вместо фактических функций F дает:

Кодирование количества ненулевых положений:

Формат l_R-битового представления мантиссы и порядка также имеет преимущества при кодировании нескольких ненулевых положений. Кодирование количества ненулевых положений v определяется посредством:

Можно легко видеть, что умножение двух аппроксимирующих функций может быть существенно более легким в формате мантиссы и порядка, чем в формате с многократно увеличенной точностью. Основное преимущество, однако, заключается в том, что когда изобретатели хотят уменьшить сложность, тогда используя l_R-битовое представление мантиссы и порядка, каждая из F'(n,k) и F'(m-1,k-1) может быть предварительно сохранена с использованием только двух слов (произведение их l_R-битовой мантиссы и суммы их порядка также может быть предварительно сохранено). Это позволяет быстрее выполнять кодирование v без какого-либо существенного требуемого объема постоянного запоминающего устройства (ROM).

Фиг.2 представляет собой блок-схему декодера 200. Как показано, декодер 200 содержит схему 206 комбинаторного декодирования, схему 210 восстановления сигнала, схему 204 другого декодирования и генератор 108 комбинаторной функции. Во время работы комбинаторное кодовое слово принимается схемой 206 комбинаторного декодирования. Схема 206 комбинаторного декодирования подает n и d на генератор комбинаторной функции и принимает в ответ F'(n,d). Схема 302 декодирования затем создает вектор x_i, основанный на F'(n,d). Схема 206 работает аналогично схеме 106 за исключением того, что вычитание заменяется операциями сложения. Другими словами, . Вектор x_i подается на схему 210 восстановления сигнала, где выходной сигнал (например, речевой сигнал, аудиосигнал, сигнал изображения, видеосигнал или другие сигналы) создается на основе x_i и других параметров от схемы 204 другого декодирования. Более конкретно, другие параметры могут включать в себя любое количество параметров восстановления сигнала, связанных с парадигмой кодирования сигнала, используемой в конкретном варианте осуществления. Они могут включать в себя, но не ограничиваются ими, параметры масштабирования сигнала и энергии и параметры формирования спектра и/или синтезирующего фильтра. Обычно эти параметры используются для масштабирования энергии и/или спектральной формы вектора x_i восстановленного сигнала таким образом, чтобы воспроизводить окончательный выходной сигнал.

Фиг.3 представляет собой блок-схему последовательности операций, изображающую работу генератора комбинаторной функции по фиг.1 и фиг.3. Более конкретно, логическая последовательность 300 операций на фиг.3 изображает эти этапы генератора 108 комбинаторной функции для получения F'(n,d). Логическая последовательность операций начинается в позиции 301, 302, где принимаются входные величины n и d. В позиции 303 накопитель A устанавливается в 0. В позиции 304 счетчик i устанавливается равным n-d+1. В позиции 306 логарифмическая аппроксимация P'(i) добавляется в накопитель A. В позиции 310 счетчик i получает приращение 1. Позиции 306 и 310 повторяются в цикле до тех пор, пока содержимое счетчика i не станет больше n. В позиции 312 проверяется i>n и завершается цикл, когда i становится больше n. На этом этапе накопитель содержит логарифмическую аппроксимацию числителя комбинаторной функции F(n,d). Логарифмическая аппроксимация знаменателя комбинаторной функции Q'(d) вычитается из содержимого накопителя в позиции 316, и получается логарифмическая аппроксимация комбинаторной функции. В позиции 318 берется экспоненциальная аппроксимация R'(A) содержимого накопителя для генерирования аппроксимации B комбинаторной функции. В позиции 314 B выводится в качестве F'(n,d).

Хотя использование комбинаторного вычисления с уменьшенной сложностью, описанного выше, служит для значительного снижения сложности, вычисление этих функций все же вносит существенный вклад в сложность способов кодирования и декодирования. Чтобы решить этот вопрос, некоторые варианты осуществления настоящего изобретения обеспечивают адаптивное переключение между способами кодирования и декодирования положений импульсов и/или величин импульсов, чтобы уменьшить количество моментов времени, когда должно выполняться вычисление комбинаторной функции.

Возвращаясь снова к уравнениям 19 и 20, а также к их соответствующим уравнениям 25 и 26 реализации с уменьшенной сложностью, отмечается, что процесс кодирования в уравнении 19 и уравнение 25 требуют v вычислений комбинаторных функций F и F' соответственно. Аналогично, уравнения 20 и 26 требуют v-1 вычислений этих функций. Декодирование положений импульсов и величины импульса является итеративным, и, следовательно, количество моментов времени, когда вычисляются эти функции, обычно значительно больше. В декодере количество вычислений этих функций увеличивается линейно с количеством ненулевых положений или занятых положений v. Чтобы уменьшить сложность кодирования/декодирования положений импульса и/или величин импульса, некоторые альтернативные варианты осуществления изобретения обеспечивают способ кодирования и декодирования положения импульса и/или величин импульса, который требует меньшего количества вычислений этих комбинаторных функций. В этих альтернативных вариантах осуществления изобретатели предлагают модифицировать уравнения 19 и 20 и посредством расширения модифицировать уравнения 25 и 26, чтобы селективно кодировать незанятые положения.

Рассмотрим сначала уравнение 20 и соответствующее уравнение 26 с уменьшенной сложностью. Если определим

тогда уравнение 20 можно переписать следующим образом:

И уравнение 26 можно переписать следующим образом:

Отметьте, что уравнения 20а и 26а подобны по структуре уравнениям 19 и 25 соответственно, причем p_k заменено на p'_k, n заменено на m-1, и занятые положения v заменены на v-1, т.е. кодирование величин импульса может рассматриваться как кодирование положения v-1 импульсов, размещенных в m-1 расположениях, где занятые положения идентифицируются посредством p'_k. Фактически, кодирование величин импульса может рассматриваться как величины m_j занятых импульсов, преобразуемых для генерирования псевдоположений, определенных членами p_j и u_j. Таким образом, любое изменение в способе кодирования положений импульса легко может быть расширено на кодирование величин импульса, и наоборот.

Согласно некоторым альтернативным вариантам осуществления изобретатели тогда предполагают оптимизацию кодирования величин импульса и/или положений импульса для уменьшения количества требуемых вычислений комбинаторных функций. Перед кодированием/декодированием положений импульса v кодируется/декодируется (уравнение 27). Следовательно, если удвоенное количество ненулевых положений больше количества расположений, т.е. 2·v>n, тогда количество незанятых положений u₁, u₂, …, u_v меньше количества занятых положений v. Таким образом, в таких случаях кодирование/декодирование незанятых положений с использованием уравнения, подобного уравнению 19 (или 25), будет приводить к меньшему количеству вычислений комбинаторных функций и, следовательно, будет иметь меньшую сложность. Чтобы проиллюстрировать это математически, определим сначала u_k в качестве незанятых положений, и U пусть будет множеством незанятых положений, т.е.

Отметим, что размер U равен n-v. Теперь, когда 2·v>n, код для положения теперь вычисляется как:

или

Аналогично для кодирования величин, если 2·(v-1)>(m-1), тогда

или

где u'_k принадлежит множеству U', определенному как

и p'_k являются теми, которые определены в уравнении 28.

Изобретатели теперь оценивают то, как предлагаемый способ селективного кодирования незанятых положений может уменьшить сложность посредством применения предлагаемого метода при кодировании 27 импульсов в 280 расположениях, т.е. n=280 и m=27. Так как 2·m<n, то может не требоваться предлагаемый подход кодирования для генерирования кода для положений (C_π) импульса. Однако для кодирования величины импульса предлагаемый метод может выгодно использоваться.

Оказывается, что без использования предлагаемого метода сложность наихудшего случая алгоритма кодирования/декодирования (когда используются комбинаторные функции малой сложности) в данном конкретном примере наблюдается тогда, когда количество ненулевых положений (v) находится между 25 и 27, т.е. между m и m-2. Когда v=25, тогда использование уравнения 26 потребует 24 вычисления комбинаторной функции для кодирования и несколько больше для декодирования. Использование предлагаемого метода (уравнение 26z) в такой ситуации потребует вычисление комбинаторной функции только дважды в кодере и значительно меньшее количество раз в декодере при сравнении с другими методами декодирования.

Согласно предлагаемому методу кодирования/декодирования, согласующемуся с вариантами осуществления настоящего изобретения, сложность наихудшего случая в данном примере тогда, когда v близко к m/2. В данном случае кодирование и декодирование количества ненулевых положений v, используя уравнение 27, вносит существенный вклад в сложность. Сохранение параметров (запоминание 54 слов требуется в данном примере), как описано в разделе «Кодирование количества ненулевых положений», дополнительно уменьшает сложность.

Таблица ниже показывает снижение сложности, когда предлагаемый способ кодирования незанятых положений используется для кодирования 27 импульсов в 280 расположениях, и кодирование выполняется 2 раза в 20-мс кадре. Таблица также показывает преимущество, получаемое от сохранения параметров, используемых при вычислении кода для количества ненулевых положений (уравнение 27). Из таблицы изобретатели заключают, что селективное кодирование незанятых положений, приводящее к снижению сложности на 0,6 WMOP (с 3,59 до 2,9), и, если также сохраняются параметры, используемые в уравнении 27, тогда уменьшение