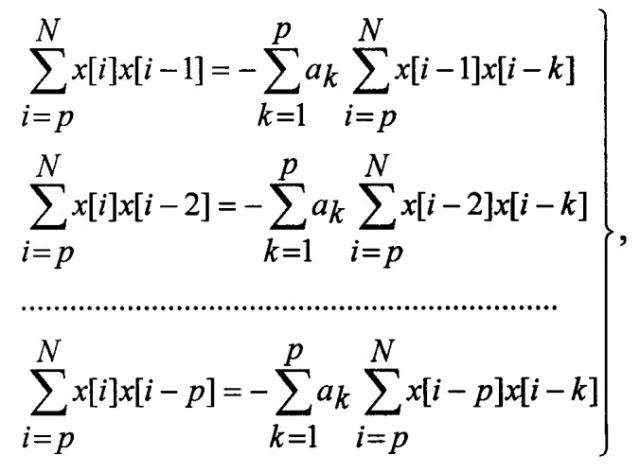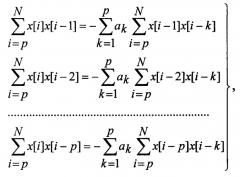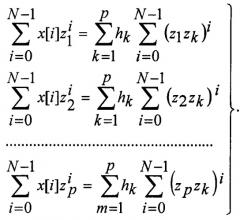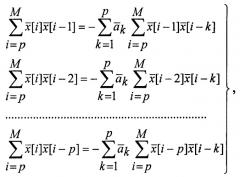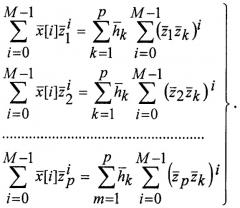Способ и устройство для цифрового сжатия и восстановления сигналов

Способ и устройство для цифрового сжатия и восстановления сигналов

Иллюстрации

Показать все

Реферат

Изобретение относится к области цифровой обработки сигналов и информационно-измерительной техники и может быть использовано для анализа, сжатия-восстановления, выделения и измерения параметров колебательных компонент сигналов в системах телеметрии, телеуправления и многоканальных системах сбора и обработки данных.

Известны и широко применяются способы и реализующие их устройства для цифрового сжатия и восстановления сигналов, основанные на полиноминальной, сплайновой и Фурье-аппроксимации сигналов [1, 2, 3, 4], и последующей интерполяции данных. Их основным недостатком является низкая точность, особенно для знакопеременных сигналов, и значительное влияние на получаемые результаты случайных шумов, неизбежно наложенных на сигнал.

Из известных наиболее близким по технической сущности является способ сжатия и восстановления сигналов, основанный на представлении выборочных данных в виде конечной линейной комбинации экспонент (колебаний, характеризуемых амплитудами, начальными фазами, частотами и коэффициентами затухания), параметры которых рассчитываются по методу наименьших квадратов Прони (С.Л.Марпл - мл. Цифровой спектральный анализ и его приложения. Пер. с англ.- М.: Мир, 1990. - 584 с., стр.365-391 [5]). Данный способ реализован в системе для измерения параметров и спектрального анализа слабых сигналов (Ионов С.В., Мясникова М.Г., Цыпин Б.В., Шаповал И.О. Модульная система для измерения параметров и спектрального анализа слабых сигналов // Измерительная техника. - 2011. - №4 [5]).

В этом способе задают число экспонент (колебаний), используемых для сжатого представления сигнала, непрерывный сигнал дискретизируют с постоянным шагом, вычисляют коэффициенты характеристического уравнения путем решения системы уравнений, составленных с использованием дискретных значений сигнала по методу наименьших квадратов, находят корни характеристического уравнения, используют их совместно с дискретными значениями сигнала во второй системе уравнений, составленных по методу наименьших квадратов, рассчитывают по корням этой системы уравнений и корням характеристического уравнения параметры колебаний, по которым сигнал восстанавливают.

В способе-прототипе для представления в сжатом виде непрерывного сигнала x(t), заданного своими дискретными значениями х[1],…,x[N], полученными с постоянным шагом дискретизации Т, используется функция дискретного времени (n), представляющая собой сумму р экспонент (колебаний):

где 1≤n≤N, N>2р;

h_k=A_kexp(jθ_k) - комплексная амплитуда, представляющая независимый от времени параметр экспоненты;

z_k=exp[(α_k+j2πf_k)T] - комплексная экспонента, описывающая параметр экспоненты, зависимый от времени.

Так как исходные данные x(n) являются действительными числами, то экспоненты h_k и z_k появляются, в общем случае, комплексно-сопряженными парами равной амплитуды.

Известный способ реализует следующую последовательность действий.

1. Исходя из априори известного вида сигнала x(t) или его предварительного анализа (см. [4] гл.8) и требуемой точности восстановления, задают число р экспонент (колебаний), используемых для представления сигнала.

2. Непрерывный сигнал x(t) дискретизируют с постоянным шагом T, то есть представляют его дискретными значениями х[1],…, x[N], причем число дискретных значений N>>2p.

3. Рассчитывают параметры экспонент h_k и z_k в следующей последовательности:

3.1. Составляют по методу наименьших квадратов систему уравнений

из решения которой находят коэффициенты авторегрессии а_k.

3.2.Подставляют значения коэффициентов авторегрессии а_k в характеристическое уравнение

3.3. z^p+a₁z^p-l+…+a_p=0

и находят его корни z_k, представляющие параметры экспонент, зависимые от времени.

3.4. Минимизируя сумму квадратов ошибок по каждому параметру h_k, составляют и решают вторую систему уравнений, вычисляя ее корни h_k, представляющие параметры экспонент, независимые от времени:

3.5.Рассчитывают параметры колебаний: частоты

,

коэффициенты затухания амплитуды амплитуды A_k=|h_k| [В] и начальные фазы θ_k=argh_k [рад].

4. Восстанавливают по полученным значениям частот f_k, коэффициентов затухания амплитуды α_k, амплитуд А_k и начальных фаз θ_k исходный сигнал.

Известный способ при значительном уровне аддитивного шума, наложенного на сигнал, часто не обеспечивает удовлетворительных результатов. Значения коэффициентов затухания и частот часто намного превышают их истинные значения. Для решения этой проблемы предлагается ([4, стр.376, 384-390]) использовать значения р, превышающие число необходимых, исходя из вида сигнала. При практическом применении способа такое решение приводит к существенному возрастанию трудоемкости и продолжительности расчетов, что препятствует реализации способа на микроконтроллерах и использованию в составе мобильных систем реального времени. Кроме того, недостатком известного способа является то, что одновременно с восстановлением исходного сигнала происходит и восстановление сопровождающих его шумов.

Целью предлагаемого способа является снижение трудоемкости и продолжительности расчетов при значительном уровне аддитивного шума, наложенного на сигнал, что обеспечит возможность реализации на микроконтроллерах и использованию в составе мобильных систем реального времени, а также снижение уровня шумов в восстановленном сигнале.

Указанная цель достигается тем, что в способе цифрового сжатия и восстановления сигналов, основанном на представлении сигналов линейной комбинацией заданного числа экспонент, включающем дискретизацию сигнала, вычисление коэффициентов характеристического уравнения путем решения системы уравнений, составленных с использованием значений сигнала по методу наименьших квадратов, нахождение корней характеристического уравнения, использование их совместно со значениями сигнала во второй системе уравнений, составленных по методу наименьших квадратов, расчет по корням этой системы уравнений и корням характеристического уравнения параметров колебаний, по которым сигнал восстанавливают, предварительно производят разбиение дискретных отсчетов сигнала на блоки равной длительности, проводят численное интегрирование сигнала в каждом блоке, используют полученные интегральные значения в качестве исходных для расчетов, а полученные результаты пересчитывают в параметры колебаний, представляющих исходный сигнал, при этом после расчета параметров колебаний исключают из дальнейшего рассмотрения колебания с малой относительно остальных амплитудой и колебания с большим относительно остальных коэффициентом затухания амплитуды.

В заявляемом способе для представления в сжатом виде непрерывного сигнала x(t), заданного своими дискретными значениями х[1],…,x[N], полученными с постоянным шагом дискретизации Т, также используется функция дискретного времени , представляющая собой сумму р экспонент:

где 1≤n≤N, N>2р;

h_k=A_kехр(jθ_k) - комплексная амплитуда, представляющая независимый от времени параметр колебания;

z_k=exp[(α_k+j2πf_k)T] - комплексная экспонента, описывающая параметр колебания, зависимый от времени.

Так как исходные данные х(n) являются действительными числами, то экспоненты h_k и z_k появляются, в общем случае, комплексно-сопряженными парами равной амплитуды.

Предлагаемый способ реализует следующую последовательность действий.

1. Исходя из априори известного вида сигнала x(t) или его предварительного анализа и требуемой точности восстановления, задают число р экспонент (колебаний), используемых для представления сигнала.

2. Непрерывный сигнал частот f_k, коэффициентов затухания амплитуды α_k, амплитуд А_k и начальных фаз θ_k дискретизируют с постоянным шагом Т, то есть представляют его дискретными значениями х[1],…, x[N], причем число дискретных значений N>>2p.

3. Разбивают последовательность дискретных значений сигнала на равные блоки длительностью m, число которых М несколько больше 1р.

4. Проводят численное интегрирование сигнала в каждом блоке.

5. Используют полученные интегральные значения для расчета параметров экспонент (колебаний) h_k и z_k в следующей последовательности:

5.1. Составляют по методу наименьших квадратов систему уравнений

из решения которой находят коэффициенты авторегрессии .

5.2.Подставляют значения коэффициентов авторегрессии в характеристическое уравнение

и находят параметры , представляющие параметры колебаний, зависимые от времени.

5.3.Минимизируя сумму квадратов ошибок по каждому параметру , составляют и решают вторую систему уравнений, вычисляя ее корни , представляющие параметры колебаний, независимые от времени:

5.4.3начения и , полученные для проинтегрированного сигала, пересчитываю в параметры колебаний, представляющих исходный сигнал - частоты, коэффициенты затухания амплитуды, амплитуды и начальные фазы - соответственно:

, .

5.5. Исключают из дальнейшего рассмотрения колебания с малой относительно остальных амплитудой и колебания с большим относительно остальных коэффициентом затухания амплитуды.

6. Восстанавливают по оставшимся значениям частот f_k, коэффициентов затухания амплитуды α_k, амплитуд А_k и начальных фаз θ_k исходный сигнал.

Технический результат - уменьшение трудоемкости и, следовательно, продолжительности расчетов достигается за счет того, что частота дискретизации сигналов определяется тактом работы аналого-цифрового преобразователя и, как правило, высока. Сжатие сигналов происходит по кадрам (фрагментам), в которые входят от нескольких сот до нескольких тысяч дискретных значений. При разбивании кадра на блоки и интегрировании дискретных отсчетов сигнала в пределах блоков, во-первых, происходит уменьшение исходных данных для расчетов (вместо N-М), а во-вторых, случайные шумы усредняются за счет интегрирования, отношение сигнал-шум в проинтегрированном сигнале больше, что позволяет использовать меньшие значения p.

Кроме того, за счет предварительного интегрирования и исключения из рассмотрения характерных для шумов, сопровождающих сигнал, колебаний с малой относительно остальных амплитудой и колебаний с большим относительно остальных коэффициентом затухания амплитуды в восстановленном сигнале отношение сигнал-шум значительно возрастает.

Технический результат достигается также за счет применения нового устройства для реализации заявленного способа цифрового сжатия и восстановления сигналов, содержащего аналого-цифровой преобразователь, интегратор, запоминающее устройство, блок вычисления коэффициентов авторегрессии, блок вычисления параметров экспонент, зависимых от времени, блок вычисления параметров экспонент, независимых от времени, блок расчета параметров колебаний, блок восстановления сигнала, соединенные последовательно, а также таймер, выход которого соединен с управляющими входами интегратора и запоминающего устройства, причем второй вход блока вычисления параметров экспонент, независимых от времени, соединен с выходом запоминающего устройства, а второй вход блока расчета параметров колебаний подключен к выходу блока вычисления коэффициентов авторегрессии.

На фиг.1 приведена функциональная схема устройства, реализующего заявляемый способ цифрового сжатия и восстановления сигналов.

Устройство для цифрового сжатия и восстановления сигналов содержит аналого-цифровой преобразователь 1, интегратор 2, запоминающее устройство 3, блок 4 вычисления коэффициентов авторегрессии, блок 5 вычисления параметров экспонент, зависимых от времени, блок 6 вычисления параметров экспонент, независимых от времени, блок 7 расчета параметров колебаний, блок 8 восстановления сигнала и таймер 9. Аналого-цифровой преобразователь 1, интегратор 2 и запоминающее устройство 3 соединены последовательно. Управляющие входы интегратора 2 и запоминающего устройства 3 подключены к выходу таймера 9. Выход запоминающего устройства 3 соединен с входом блока 4 вычисления коэффициентов авторегрессии и первым входом блока 6 вычисления параметров экспонент, независимых от времени. Выход блока 4 вычисления коэффициентов авторегрессии соединен с входом блока 5 вычисления параметров экспонент, зависимых от времени, и входом блока 7 расчета параметров колебаний, к выходу которого подключен блок 8 восстановления сигнала.

Все элементы, входящие в состав устройства, могут быть реализованы в виде отдельных функциональных узлов, например, блоки 2-7, 9 на программируемых логических интегральных схемах (ПЛИС), блок 8 - ЦАП или все - программным способом при использовании микроконтроллеров, оснащенных аналого-цифровыми преобразователями.

Работает устройство для цифрового сжатия и восстановления сигналов следующим образом. Аналого-цифровой преобразователь 1 осуществляет дискретизацию с шагом Т и квантование непрерывного входного сигнала x(t), преобразуя его в последовательность N цифровых отсчетов х[1],…,x[N]. Частота дискретизации высокая и определяется возможностями аналого-цифрового преобразователя 1. В интеграторе 2 выполняется численное интегрирование дискретизированного сигнала на интервалах времени m, задаваемых таймером 9. Число интервалов М устанавливается до начала работы не меньшим, чем удвоенное число экспонент, требуемых для представления сигнала с заданной точностью, и зависит от ожидаемого вида сигнала x(t). Последовательность интегрированных значений сигнала накапливается в запоминающем устройстве 3 за время существования сжимаемого кадра (фрагмента) сигнала. Затем накопленные значения передаются в блок 4 вычисления коэффициентов авторегрессии , а в запоминающем устройстве 3 накапливаются последовательность интегрированных значений следующего фрагмента сигнала. В блоке 4 вычисления коэффициентов авторегрессии используют интегральные значения сигнала для нахождения корней системы уравнений, составленных по методу наименьших квадратов.

Вычисленные значения коэффициентов авторегрессии передаются в блок 5 вычисления параметров экспонент , зависимых от времени. Результаты вычислений являются корнями характеристического уравнения и характеризуют частоты f_k и коэффициенты затухания амплитуд α_k колебаний, представляющих сигнал. Значения параметров экспонент , зависимых от времени, совместно с интегральными значениями сигнала поступают в блок 6 вычисления параметров экспонент , независимых от времени. В блоке 6 вычисления параметров экспонент , независимых от времени, происходит определение корней системы уравнений, составленных по методу наименьших квадратов для подгонки независимых от времени параметров экспонент, представляющих проинтегрированный сигнал, при условии, что зависимые от времени параметры этих экспонент известны.

Блок 7 расчета параметров колебаний на основе полученных значений и находит параметры колебаний - частоты f_k, коэффициенты затухания амплитуды α_k, амплитуды А_k и начальные фазы θ_k. При необходимости в блоке 7 расчета параметров колебаний исключают из дальнейшего рассмотрения колебания с малой относительно остальных амплитудой и колебания с большим относительно остальных коэффициентом затухания амплитуды.

В блоке 8 восстановления сигнала полученные значения параметров колебаний используются для синтеза с помощью цифро-аналогового преобразования колебаний, которые после суммирования их мгновенных значений формируют восстановленный сигнал x(t).

При использовании устройства для цифрового сжатия и восстановления сигналов в канал (проводной или беспроводной) передачи информации в зависимости от конкретной решаемой задачи и конкретного исполнения блоков (их вычислительной мощности на передающей стороне) могут быть реализованы различные варианты разделения блоков на передающие и приемные. В канал передачи информации могут поступать:

а) проинтегрированные значения сигнала после интегратора 2;

б) накопленная за время сжимаемого фрагмента сигнала последовательность проинтегрированных значений после запоминающего устройства 3;

в) значения коэффициентов авторегрессии и значения параметров экспонент , зависимых от времени;

г) значения зависимых от времени параметров экспонент и независимых от времени параметров экспонент;

д) значения параметров колебаний - частоты f_k, коэффициенты затухания амплитуды α_k, амплитуды А_k и начальные фазы θ_k.

В последних случаях г) и д) объем передаваемой по каналу информации минимален, а требования к вычислительной мощности блоков на передающей стороне максимальны.

Использованные источники

1. Айфичер, Эммануил С., Джервис, Барри У. Цифровая обработка сигналов. - М.: Вильямс, 2004. - 992 с.

2. Попов Б.А., Теслер Г.С. Вычисление функций на ЭВМ. Справочник. - Киев: Наукова думка, 1984. - 600 с.

3. Патент RU №94028881 от 20.06.1996.

4. Патент RU №2099720 от 20.12.1997.

5. Марпл - мл. С.Л. Цифровой спектральный анализ и его приложения. Пер. с англ. - М.: Мир, 1990. - 584 с.

6. Ионов С.В., Мясникова М.Г., Цыпин Б.В., Шаповал И.О. Модульная система для измерения параметров и спектрального анализа слабых сигналов // Измерительная техника. - 2011. - №4.

1. Способ цифрового сжатия и восстановления сигналов, основанный на представлении сигналов линейной комбинацией заданного числа экспонент, включающий дискретизацию сигнала, вычисление коэффициентов характеристического уравнения путем решения системы уравнений, составленных с использованием значений сигнала по методу наименьших квадратов, нахождение корней характеристического уравнения, использование их совместно со значениями сигнала во второй системе уравнений, составленных по методу наименьших квадратов, расчет по корням этой системы уравнений и корням характеристического уравнения параметров колебаний, по которым сигнал восстанавливают, отличающийся тем, что предварительно производят разбиение дискретных отсчетов сигнала на блоки равной длительности, проводят численное интегрирование сигнала в каждом блоке, используют полученные интегральные значения в качестве исходных для расчетов, а полученные результаты пересчитывают в параметры колебаний, представляющих исходный сигнал.

2. Способ цифрового сжатия и восстановления сигналов по п.1, отличающийся тем, что после расчета параметров колебаний исключают из дальнейшего рассмотрения колебания с малой относительно остальных амплитудой и колебания с большим относительно остальных коэффициентом затухания амплитуды.

3. Устройство цифрового сжатия и восстановления сигналов, содержащее аналого-цифровой преобразователь, интегратор, запоминающее устройство, блок вычисления коэффициентов авторегрессии, блок вычисления параметров экспонент, зависимых от времени, блок вычисления параметров экспонент, независимых от времени, блок расчета параметров колебаний, блок восстановления сигнала, соединенные последовательно, а также таймер, выход которого соединен с управляющими входами интегратора и запоминающего устройства, причем второй вход блока вычисления параметров экспонент, независимых от времени, соединен с выходом запоминающего устройства, а второй вход блока расчета параметров колебаний подключен к выходу блока вычисления коэффициентов авторегрессии.