Способ определения модуля упругости бетона в упругих железобетонных конструкциях балочного типа

Способ определения модуля упругости бетона в упругих железобетонных конструкциях балочного типа

Иллюстрации

Показать все

Реферат

Изобретение относится к области строительства и предназначено для диагностики и контроля качества железобетонных конструкций балочного типа вибрационным методом.

Известен способ определения модуля упругости бетона в железобетонной конструкции путем испытания образцов (кубиков), специально изготавливаемых одновременно с бетонированием конструкции либо в заводских условиях, либо на стройплощадке (см. ГОСТ 10180-90 Бетоны. Методы определения прочности по контрольным образцам).

Этот способ имеет недостаток, который заключается в том, что со временем физико-механические свойства бетона изменяются в зависимости от условий эксплуатации и в случае необходимости для определения модуля упругости бетона следует прибегать к другим методам.

Известен также способ определения модуля упругости бетона в упругих железобетонных балках по максимальному прогибу w₀, который следует из известной формулы из курса железобетонных конструкций для шарнирно опертой балки, нагруженной равномерно распределенной нагрузкой q (см. Байков В.Н., Сигалов Е.Е. Железобетонные конструкции. - М.: Стройиздат, 1984. - С.245):

где ℓ - пролет балки; E_b - модуль упругости бетона; I_red - приведенный момент инерции сечения балки. Согласно этому способу контролируемую балку загружают некоторой равномерно распределенной нагрузкой, не вызывающей появления пластических деформаций в конструкции, измеряют максимальный прогиб и по второй формуле из (1) подсчитывают значение модуля упругости.

Этот способ обладает большой трудоемкостью из-за необходимости выполнения операции загружения конструкции.

Задача, на решение которой направлено изобретение, состоит в снижении трудоемкости способа определения модуля упругости бетона в железобетонных конструкциях балочного типа как в заводских условиях при их изготовлении, так и находящихся в условиях эксплуатации.

Решение этой задачи достигается тем, что в способе определения модуля упругости бетона в упругих железобетонных конструкциях балочного типа, заключающемся в установке их на стенде, закреплении концов по схеме шарнирного опирания, нагружении и измерении физических параметров, с помощью которых по аналитическим зависимостям подсчитывают значение модуля упругости бетона, согласно изобретению для конструкций определенного типа изготавливают 5…8 эталонных изделий, модуль упругости которых изменяется в определенном диапазоне значений, в каждом из эталонных изделий возбуждают свободные поперечные или продольные колебания на основной частоте (или вынужденные колебания на первой резонансной частоте), измеряют эту частоту и по полученным значениям строят аналитическую зависимость «модуль упругости бетона - частота колебаний»; при диагностике изделия серийного изготовления определяют его основную (или первую резонансную) частоту колебаний и по полученной аналитической зависимости подсчитывают модуль упругости бетона.

Сущность заявляемого способа поясняется чертежами, приведенными на фигурах 1…3.

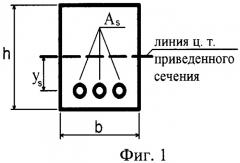
На фиг.1 изображено прямоугольное поперечное сечение балки с указанием некоторых геометрических размеров, входящих в используемые расчетные формулы;

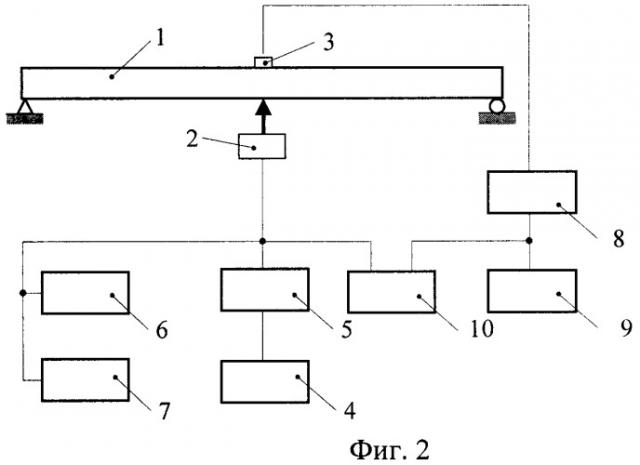
На фиг.2 представлена функциональная схема экспериментальной установки для определения первой резонансной частоты поперечных колебаний, где 1 - контролируемое изделие, 2 - излучатель механических колебаний, 3 - приемник механических колебаний, 4 - генератор синусоидальных колебаний, 5 - усилитель мощности, 6 - частотомер, 7 - цифровой вольтамперметр, 8 - предварительный усилитель, 9 - анализатор спектра, 10 - электронный осциллограф.

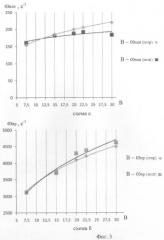
На фиг.3 представлены графики изменения модуля упругости в железобетонных балках в зависимости от основной частоты собственных поперечных колебаний (схема а) и основной частоты собственных продольных колебаний (схема б).

Физическую сущность предлагаемого способа можно пояснить следующими рассуждениями.

В работе Коробко В.И. Изопериметрический метод в строительной механике: Теоретические основы изопериметрического метода. - Т.1. - М.: Изд-во АСВ, 1997. - С.346-349 для упругих балок получена фундаментальная закономерность, связывающая максимальный прогиб балок w₀, нагруженных равномерно распределенной нагрузкой q, с их основной частотой колебаний в ненагруженном состоянии ω:

где m - погонная масса балки. В этой закономерности вместо основной частоты колебаний упругих балок может использоваться первая резонансная частота колебаний, так как из курса строительной механики хорошо известно, что эти характеристики незначительно отличаются друг от друга (см. Коробко В.И., Коробко А.В. Строительная механика: Динамика и устойчивость стержневых систем. - М.: Изд-во АСВ, 2008. - С.20-24). Как видно из выражения (3), произведение w₀ω² не зависит от вида граничных условий, поэтому оно справедливо и для балок, работающих в условиях эксплуатации с любыми неопределенными граничными условиями, а при изготовлении конструкций в заводских условиях можно моделировать на стенде только условия шарнирного опирания.

Из формулы (3) можно выразить максимальный прогиб через основную (или первую резонансную частоту колебаний):

Подставляя это выражение во вторую формулу из (1), получим:

Из этой формулы видно, что величина модуля упругости бетона функционально связана с основной (или первой резонансной) частотой поперечных колебаний.

В случае использования продольных колебаний формула (4) примет следующий вид:

где A_red - площадь приведенного сечения балки (см. Коробко В.И., Юров А.П. Применение продольных колебаний для диагностики железобетонных конструкций / Материалы Всероссийской научно-технической конференции «Диагностика веществ, изделий и устройств». - Орел, ОрелГТУ, 1999. - С.118-120).

Однако, как показали экспериментальные исследования, при использовании этих зависимостей для определения модуля упругости бетона по частоте колебаний получается довольно значительная погрешность. Это объясняется тем, что бетон обладает упругопластическими свойствами и пластическая составляющая оказывает свое влияние на результаты расчета по формулам (4) и (5), которые получены, исходя из предположения об идеальной упругости бетона. Поэтому функциональную связь

E_b-ω целесообразно получать для каждого типа конструкций, используя эталонные изделия, выполненные из бетона в определенном диапазоне значений модуля упругости при одинаковом их армировании.

Способ осуществляется следующим образом. Для конструкций определенного типа, например для железобетонных балок марки ПБ, изготавливают 5…8 эталонных изделий, класс бетона в которых (модуль упругости) постепенно возрастает от В-7,5 до В-30. Каждую из этих балок устанавливают на испытательном стенде, закрепляют ее концы по схеме шарнирного опирания и возбуждают в ней свободные поперечные или продольные колебания с помощью механического удара или внезапного снятия некоторой статической нагрузки (в случае поперечных колебаний). Используя какой-либо частотомер, например виброанализатор «Вибран-2», измеряют основную частоту колебаний.

Если используется режим воздействия вынужденными колебаниями, то на контролируемую балку 1 в средней части пролета закрепляют с одной стороны излучатель колебаний 2, например электродинамический вибровозбудитель поперечных колебаний, а с другой стороны - приемник механических колебаний 3 (первичный преобразователь виброперемещений). С помощью генератора синусоидальных колебаний 4 и усилителя мощности 5 возбуждают в конструкции колебания в требуемом диапазоне частот, поддерживая энергию этих колебаний строго на одном уровне. При этом частоту и амплитуду электрического сигнала, подаваемого на вход вибровозбудителя поперечных колебаний 2, контролируют частотомером 6 и цифровым вольтамперметром 7. Сигнал с приемника механических колебаний усиливается с помощью предварительного усилителя 8, а с помощью анализатора спектра 9 снимают амплитудно-частотную характеристику контролируемой конструкции, по которой определяют резонансную частоту колебаний. Кроме того, в схему включен электронный осциллограф 10 для визуализации колебательного процесса.

По полученным результатам строят аппроксимирующую функцию «модуль упругости бетона - частота колебаний».

Далее, при диагностике изделия серийного изготовления определяют ее основную (или первую резонансную) частоту колебаний и с помощью построенной аппроксимирующей функции находят действительный модуль упругости бетона.

Пример реализации способа.

Для проведения испытаний были изготовлены 5 железобетонных эталонных балок длиной 2,6 м с поперечным сечением 120×140 мм, балки армированы в нижней зоне одним арматурным стержнем ⌀12 мм A-III. Класс бетона балок был принят изменяющимся ступенчато от В-7,5 до В-30. Балки испытывались в режиме свободных затухающих поперечных и продольных колебаний. При этом возбуждение колебаний осуществлялось с помощью поперечного и продольного механического удара. После статистической обработки экспериментальных данных были получены следующие результаты:

Таблица 1
Результаты измерения основной частоты поперечных колебаний эталонных балок и отклонения экспериментальных значений от теоретических, полученных по формуле (4)
Частоты колебаний	Класс бетона
В-7,5	В-15	В-20	В-22,5	В-30
ωпоп(эксп), с-1	161	182	188	192	184
ωпоп(теор), с-1	154	185	200	206	220
Отклонение, %	4,55	1,62	6	6,8	16,36

Таблица - 2
Результаты измерения основной частоты продольных колебаний эталонных балок и отклонения экспериментальных значений от теоретических, полученных по формуле (5)
Частоты колебаний	Класс бетона
В-7,5	В-15	В-20	В-22,5	В-30
ωпр(эксп), с-1	3121	3705	4296	4390	4616
ωпр(теор), с-1	3159	3787	4101	4214	4496
Отклонение, с-1	38	82	195	176	120
Отклонение, %	1,2	2,17	4,75	4,18	2,67

Как видно из таблиц, лучшая сходимость экспериментальных и теоретических результатов достигается при использовании продольных колебаний. Это объясняется тем, что при продольных колебаниях по всей длине балок все поперечные сечения вовлекаются в работу и работают в одинаковых условиях, в то время как при поперечных колебаниях приопорные участки балок деформируются менее интенсивно, чем участки, прилежащие к средней их части.

Графики зависимостей E_b-ω, построенные по табличным данным, приведены на фиг.3. Из рисунка видно, что эти зависимости носят функциональный характер и поэтому динамический параметр - основная (или первая резонансная) частота колебаний могут использоваться для определения модуля упругости бетона при диагностике железобетонных конструкций балочного типа.

По экспериментальным данным построены аппроксимирующие функции:

- при поперечных колебаниях

- при продольных колебаниях

Эти зависимости могут использоваться при диагностике конструкций рассмотренного типа серийного изготовления.

Для каждого типа железобетонных конструкций в виде балок необходимо построить свои аппроксимирующие функции. Это можно осуществить в заводских условиях при освоении выпуска определенного типа конструкций.

При реализации предлагаемого способа отпадает необходимость проведения статического нагружения конструкций.

Таким образом, технический результат - снижение трудоемкости осуществления способа определения модуля упругости бетона в железобетонных конструкциях балочного типа достигается за счет использования динамического параметра конструкции - основной (или первой резонансной) частоты поперечных (или продольных) колебаний в ненагруженном состоянии.

Способ определения модуля упругости бетона в упругих железобетонных конструкциях балочного типа, заключающийся в установке их на стенде, закреплении концов по схеме шарнирного опирания, нагружении и измерении физических параметров, с помощью которых по аналитическим зависимостям подсчитывают значение модуля упругости бетона конструкции, отличающийся тем, что для конструкций определенного типа изготавливают 5…8 эталонных изделий, модуль упругости которых изменяется в определенном диапазоне значений, в каждом из эталонных изделий возбуждают свободные поперечные (или продольные) колебания на основной частоте (или вынужденные колебания на первой резонансной частоте), измеряют эту частоту, и по полученным значениям строят аналитическую зависимость «модуль упругости бетона - частота колебаний»; при диагностике изделия серийного изготовления определяют его основную (или первую резонансную) частоту колебаний и по полученной аналитической зависимости подсчитывают модуль упругости бетона.