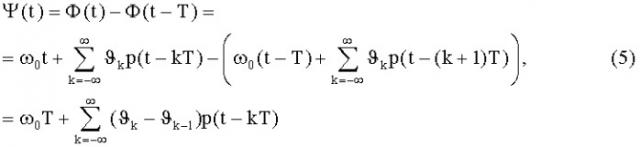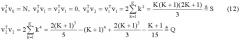Способ измерения времени прихода сигнала и устройство для его реализации

Способ измерения времени прихода сигнала и устройство для его реализации

Иллюстрации

Показать все

Реферат

Изобретение относится к радиотехнике и может использоваться для измерения времени прихода сигналов с многопозиционной квадратурной амплитудной манипуляцией (МКАМ или MQAM) на приемной позиции.

Измерение времени прихода (ВП) сигналов на приемной позиции с известными координатами имеет большое значение в системах дальней космической связи с космическими аппаратами (КА) типа Mars Polarlander, Mars Pathfinder [1] или с КА типа Voyager и Galileo [2], в том числе для определения параметров движения таких КА.

Известен ряд способов измерения ВП сигналов, в том числе с разнесенных приемных позиций [3-6], основанных на нахождении аргументов максимума двумерной кросс-корреляционной функции, потенциально дающих статистически оптимальные максимально правдоподобные оценки. Однако потенциальная точность способов [3-6] нереализуема на практике ввиду отсутствия плавно регулируемых эталонов времени и частоты [7, 8].

Известен ряд цифровых способов измерения ВП сигналов с разнесенных приемных позиций [8], основанных на нахождении аргумента максимума кросс-корреляционной функции или аргумента минимума разностных дискретных кросс-корреляционных функций (ДККФ), позволяющих реализовать потенциальную точность способов [3-6] за счет исключения погрешности дискретности путем параболической интерполяции окрестностей максимума или минимума соответствующих функций. Однако, цифровые способы измерения ВП сигналов [8-9] неприменимы при наличии неопределенности по частоте приема, что имеет место в системах дальней космической связи с космическими аппаратами. Другим недостатком цифровых способов измерения, представленных в работе [8], является низкая вычислительная эффективность на больших размерах выборки данных, поскольку они основаны на прямом вычислении ДККФ (при таком методе нахождения ДККФ количество операций умножения пропорционально квадрату длины (n) выборки данных, подобная пропорциональность обычно обозначается как O(n²)).

При измерении ВП сигнала для определения дальности до КА дальней космической связи неизбежно возникает неопределенность по частоте приема, которая может быть вызвана как разностью опорных частот на КА и на земле, так и за счет эффекта Доплера, вызываемого взаимным движением наземной приемной позиции и КА. Поэтому в таких случаях при измерении ВП сигнала необходимо находить максимум двумерной кросс-корреляционной функции с одновременным разрешением неопределенности по частоте и измерением, таким образом, частоты приема или разности частоты приема (РЧП).

В патентах [10-12] представлен ряд цифровых способов совместного измерения разности времени прихода (РВП) и РЧП сигналов с разнесенных приемных позиций, основанных на нахождении аргументов максимума двумерной ДККФ (ДДККФ), которые позволяют производить измерения при наличии движения источника сигнала или приемной позиции. Основная цель, поставленная автором патентов [10-12], посвящена снижению потоков информации передаваемых между разнесенными приемными позициями и компенсации систематической погрешности, возникающей при корреляции компрессированного и опорного сигналов. Однако, в способах совместного измерения РВП и РЧП [10-12] не решены вопросы исключения погрешности дискретности (корреляционная зависимость между РВП и РЧП [13] не позволяет очевидным способом распространить на совместные измерения подходы, изложенные в [8]) и вопросы повышения вычислительной эффективности, так как кросс-корреляционные функции в способах [10-12] порождаются прямым методом через свертку двух последовательностей данных, как и в [8], а за счет n-кратного повторения (для обеспечения поиска аргумента максимума в частотной области) количество операций умножения увеличивается и пропорционально кубу длины (n) выборки данных, т.е. O(n³).

Наиболее близким к предлагаемому способу измерения ВП сигналов, по совокупности используемых действий над сигналом, является способ [14], основанный на нахождении аргументов максимума ДДККФ (вычислительно существенно более эффективный, чем аналоги), принятый за прототип.

Согласно этому способу:

1. Принимают сигнал на двух разнесенных приемных позициях.

2. Преобразуют сигнал, полученный от одной приемной позиции в первый цифровой поток данных, который в цифровой форме представляет сигнал как ряд значений функции времени.

3. Преобразуют сигнал, полученный от другой приемной позиции во второй цифровой поток данных, который в цифровой форме представляет сигнал как ряд значений функции времени.

4. Преобразуют с использованием быстрого преобразования Фурье (БПФ) упомянутый первый цифровой поток данных в значения первого спектра, который представляет сигнал как ряд значений функции частоты S₁(k), где k - целочисленная индексная переменная, изменяющаяся в пределах длины данных.

5. Преобразуют с использованием БПФ упомянутый второй цифровой поток данных в значения второго спектра, который представляет сигнал как ряд значений функции частоты S₂(k).

6. Взаимно перемножают значения спектра одного из сигналов с комплексно сопряженными значениями спектра другого сигнала для порождения кросс-спектра.

7. Спектр одного из сигналов S_i(k), где i=1, 2 номер одного из двух спектров, преобразуют по частоте на величины m, выбираемые согласно требованиям по разрешению РЧП из целочисленного ряда значений от единицы до (N-1), где N - длина обрабатываемого цифрового потока данных, с созданием последовательности преобразованных по частоте спектров S_i,m(k), полученной из исходных спектральных составляющих сигнала по следующему правилу

где i - номер одного из двух принимаемых сигналов.

8. Значения спектров S_i,m(k), преобразованных по частоте сигналов, взаимно перемножают с комплексно сопряженными значениями спектра второго из двух исходных сигналов для порождения множества кросс-спектров.

9. Вычисляют ДДККФ сигнала с использованием обратного БПФ множества кросс-спектров.

10. Определяют разности времени прихода и частоты приема сигналов как аргументы максимума ДДККФ сигнала.

По существу способ, описанный выше [14], реализует вычислительно эффективное, по сравнению с аналогами [10-12], нахождение аргументов максимума ДДККФ с использованием при вычислении ДДККФ быстрых преобразований Фурье на основании теоремы Винера-Хинчина [15], определяющей взаимосвязь между спектром и корреляционной функцией сигнала.

В описании прототипа [14] представлена оценка объема вычислительных затрат на нахождение двумерной кросс-корреляционной функции в способе-прототипе и в аналогах, показывающая, что для выборки данных длиной n=1024 при k=n в способе-прототипе на нахождение ДДККФ требуется порядка O(k·n·log₂n+k·n) или 10 миллионов операций (страница 10 описания способа-прототипа), а в аналогах требуется от O(3·k·n·log₂n+k·n) до O(n³) или от 30 миллионов до миллиарда операций (страница 5 описания способа-прототипа).

Несмотря на существенное снижение вычислительных затрат по сравнению с аналогами одним из недостатков способа-прототипа является недостаточная вычислительная эффективность. Другим недостатком способа-прототипа является, как и у аналогов [10-12], длительное время нахождения аргумента максимума, то есть длительное время измерения.

Устройство-прототип [14] содержит первое средство приема сигналов, подключенное к устройству определения аргументов максимума ДДККФ, через последовательно включенные первый аналого-цифровой преобразователь (АЦП), первый процессор БПФ, вычислитель кросс-спектров и второй процессор БПФ. Выход устройства определения аргументов максимума ДДККФ является выходом устройства измерения. Между вторым средством приема сигналов и вторым входом вычислителя кросс-спектров последовательно включены второй АЦП и третий процессор БПФ. Между выходом первого процессора БПФ и третьим входом вычислителя кросс-спектров включено арифметическое устройство.

Недостатком устройства-прототипа является недостаточное быстродействие определения РЧП и РВП сигналов. Другим недостатком устройства-прототипа является длительное время нахождения аргумента максимума, то есть длительное время измерения.

Техническим результатом изобретения является повышение вычислительной эффективности за счет исключения неопределенности частоты приема, позволяющее исключить необходимость двумерного поиска аргументов максимума ДДККФ для сигнала с M-позиционной КАМ, и обойтись, таким образом, поиском аргумента максимума одномерной ДККФ.

Технический результат достигнут тем, что в способе измерения времени прихода сигнала М-позиционной квадратурной амплитудной манипуляцией (М=2ⁿ, где n=1, 2, … произвольное целое число большее или равное единице), включающем прием сигнала, аналого-цифровое преобразование принятого сигнала в первый цифровой поток данных, представляющий сигнал как ряд значений функции времени, преобразованных в цифровую форму, использование быстрого преобразования Фурье (БПФ) для двух сигналов, представляющего оба сигнала в виде ряда дискретных значений функции частоты S_i(k), где k - целочисленная индексная переменная, изменяющаяся в пределах длины данных, а i=1, 2 - индексная переменная, означающая порядковый номер преобразуемого с использованием БПФ цифрового потока данных в значения функции частоты, взаимное перемножение значений спектра одного из сигналов с комплексно сопряженными значениями спектра другого сигнала, порождающее кросс-спектр, вычисление дискретной кросс-корреляционной функции (ДККФ) сигнала с использованием обратного БПФ, определение времени прихода (ВП) сигнала как аргумента максимума ДККФ сигнала, согласно изобретению осуществляют квадратурное разложение первого цифрового потока данных относительно номинальной центральной частоты модулированного сигнала в соответствующее указанному потоку множество синфазных и квадратурных отсчетов, полученные синфазные и квадратурные отсчеты независимо низкочастотно фильтруют с частотой среза, соответствующей скорости манипуляции модулирующего сигнала, деленной на n, получают множество текущих фаз сигнала как аргументов комплексных чисел, в качестве действительной части которых используют соответствующие отфильтрованные синфазные отсчеты, а в качестве мнимой - соответствующие отфильтрованные квадратурные отсчеты сигнала, задерживают множество полученных текущих фаз сигнала на длительность символа модулирующего сигнала, вычитают по модулю 2π из каждой полученной текущей фазы соответствующее значение задержанной текущей фазы сигнала, а полученный разностный цифровой поток данных преобразуют с использованием БПФ в значения первой функции частоты S₁(k), исходное битовое сообщение последовательно-параллельно разделяют на синфазный битовый сигнал и квадратурный битовый сигнал, из синфазного битового сигнала последовательно-параллельным преобразованием с разрядностью 2^n-1 формируют синфазный многоуровневый сигнал, из квадратурного битового сигнала последовательно-параллельным преобразованием с разрядностью 2^n-1 формируют квадратурный многоуровневый сигнал, полученный квадратурный многоуровневый сигнал делят на синфазный многоуровневый сигнал, а от результата деления находят функцию арктангенса, сформированный арктангенсный сигнал задерживают на длительность символа, вычитают по модулю 2π из арктангенсного сигнала задержанный сигнал, отображают каждый символ полученного разностного сигнала на соответствующее количество отсчетов преобразованного в цифровую форму принятого сигнала относительно шкалы времени приемной позиции и формируют, таким образом, второй цифровой поток данных, который преобразуют с использованием БПФ в значения второй функции частоты S₂(k).

Другим техническим результатом изобретения является исключение погрешности измерений, вызываемой некратностью длительности символа сигнала и частоты выборки аналого-цифрового преобразования принятого сигнала.

Технический результат достигнут тем, что в способе измерения времени прихода сигнала согласно изобретению для сигнала, у которого длительность символа сигнала некратна частоте выборки аналого-цифрового преобразования принятого сигнала, отфильтрованные синфазные и квадратурные отсчеты дополнительно децимируют и интерполируют с обеспечением кратности частоты отсчетов первого цифрового потока данных длительности символа двухуровневого модулирующего сигнала.

Другим техническим результатом изобретения является исключение погрешности дискретности за счет использования того факта, что окрестность главного максимума дискретной кросс-корреляционной функции сигнала имеет форму параболы [13, стр.8-9], и за счет разработки оптимального, в среднеквадратическом смысле, аналитического метода оценки параметров параболы и определения аргумента ее максимума.

Технический результат достигнут тем, что в способе измерения времени прихода сигнала согласно изобретению слева и справа от аргумента максимума ДККФ сигнала выбирают по L точек указанной функции, значения ДККФ для выбранных точек и точки максимума объединяют в порядке временного следования в вектор-столбец с, из единиц формируют вектор-столбец v₀ такой же размерности, как вектор с, соответствующие выбранным точкам ДККФ аргументы выражают через индексную переменную l=0, ±1, …, ±L, где индексы l с отрицательным знаком соответствуют временам до точки максимума ДККФ, нулевой индекс l соответствует точке максимума ДККФ, а индексы l с положительным знаком соответствуют временам после точки максимума ДККФ, аргументы выбранных точек ДККФ упорядочивают так же, как и компоненты вектора с, и объединяют в вектор-столбец v₁, квадраты компонент вектора v₁ аналогично объединяют в вектор-столбец v₂, а уточненное значение ВП определяют по следующему правилу

где N=2L+1 - размерность сформированных векторов, надстрочный индекс T обозначает операцию транспонирования вектора, T_s - период дискретизации сигнала, - скалярное произведение векторов v₁ и с, коэффициент Р определяется выражением

коэффициент Q определяется другим выражением

а (NPv₂-P²v₀)^Tc - скалярное произведение разностного вектора (NPv₂-P²v₀) с вектором с.

Способ реализуется устройством измерения прихода сигнала с М-позиционной квадратурной амплитудной манипуляцией (М=2ⁿ, где n=1, 2, … произвольное целое число большее или равное единице), содержащим средство приема сигналов, вход которого является входом устройства измерения, соединенное с аналого-цифровым преобразователем (АЦП), последовательно включенные первый процессор БПФ, вычислитель кросс-спектров, второй процессор БПФ и устройство определения аргументов максимума дискретной кросс-корреляционной функции (ДККФ) сигнала, выход которого является выходом устройства измерения, при этом ко второму входу вычислителя кросс-спектров подключен третий процессор БПФ, согласно изобретению между выходом АЦП и входом первого процессора БПФ последовательно включены устройство квадратурного разложения сигнала, первый фильтр нижних частот (ФНЧ), постоянное запоминающее устройство (ПЗУ) и устройство вычитания по модулю 2π, между вторым выходом устройство квадратурного разложения сигнала и вторым входом ПЗУ включен второй ФНЧ, вычитающий вход устройства вычитания соединен с выходом ПЗУ через элемент задержки на длительность символа сигнала, а вход третьего процессора БПФ подключен к выходу формирователя битового сообщения через последовательно соединенные первый и второй последовательно-параллельные преобразователи, второе ПЗУ, второе устройство вычитания по модулю 2π и экспандер частоты дискретизации, при этом вычитающий вход устройства вычитания модулю 2π соединен с выходом второго ПЗУ через второй элемент задержки на длительность символа сигнала, а между вторым входом второго ПЗУ и вторым выходом первого последовательно-параллельного преобразователя включен третий последовательно-параллельный преобразователь.

Другим техническим результатом изобретения является исключение в устройстве погрешности дискретности за счет использования того факта, что окрестность главного максимума ДККФ сигнала имеет форму параболы, и за счет аналитического метода оценки параметров параболы и определения аргумента ее максимума.

Технический результат достигнут тем, что в устройстве измерения прихода сигнала с М-позиционной квадратурной амплитудной манипуляцией (М=2ⁿ, где n=1, 2, … произвольное целое число большее или равное единице) согласно изобретению к выходу устройства определения аргумента максимума дискретной кросс-корреляционной функции сигнала дополнительно подключено арифметическое устройство.

На фиг.1 представлен пример полной фазы сигнала при наличии частотной расстройки.

На фиг.2 представлен пример разности фаз сигналов со сдвигом на длительность символа Т.

На фиг.3 приведена структурная схема устройства, в котором реализуется предложенный способ.

Согласно предлагаемому способу:

1. Принимают сигнал.

2. Преобразуют принятый сигнал в первый цифровой поток данных, представляющий сигнал как ряд значений функции времени, преобразованных в цифровую форму.

3. Осуществляют квадратурное разложение первого цифрового потока данных относительно номинальной центральной частоты модулированного сигнала в соответствующее указанному потоку множество синфазных и квадратурных отсчетов.

4. Полученные синфазные и квадратурные отсчеты независимо низкочастотно фильтруют с частотой среза, соответствующей скорости манипуляции модулирующего сигнала, деленной на n.

5. Получают множество текущих фаз сигнала как аргументов комплексных чисел, в качестве действительной части которых используют соответствующие отфильтрованные синфазные отсчеты, а в качестве мнимой - соответствующие отфильтрованные квадратурные отсчеты сигнала.

6. Задерживают множество полученных текущих фаз сигнала на длительность символа модулирующего сигнала.

7. Вычитают по модулю 2π из каждой полученной текущей фазы соответствующее значение задержанной текущей фазы сигнала.

8. Преобразуют с использованием БПФ полученный разностный цифровой поток данных как первый цифровой поток данных в дискретные значения первой функции частоты S₁(k), где k - целочисленная индексная переменная, изменяющаяся в пределах длины данных.

9. Исходное битовое сообщение последовательно-параллельно разделяют на синфазный битовый сигнал и квадратурный битовый сигнал.

10. Из синфазного битового сигнала последовательно-параллельным преобразованием с разрядностью 2^n-1 формируют синфазный многоуровневый сигнал.

11. Из квадратурного битового сигнала последовательно-параллельным преобразованием с разрядностью 2^n-1 формируют квадратурный многоуровневый сигнал.

12. Полученный квадратурный многоуровневый сигнал делят на синфазный многоуровневый сигнал.

13. От результата деления находят функцию арктангенса.

14. Сформированный арктангенсный сигнал задерживают на длительность символа.

15. Вычитают по модулю 2π из сформированного сигнала задержанный сигнал.

16. Отображают каждый символ полученного разностного сигнала на соответствующее количество отсчетов преобразованного в цифровую форму принятого сигнала относительно шкалы времени приемной позиции и формируют, таким образом, второй цифровой поток данных.

17. Преобразуют с использованием БПФ упомянутый второй цифровой поток данных в значения второго спектра, который представляет сигнал как ряд значений функции частоты S₂(k).

18. Взаимно перемножают значения спектра одного из сигналов с комплексно сопряженными значениями спектра другого сигнала для порождения кросс-спектра.

19. Вычисляют дискретную кросс-корреляционную функцию (ДККФ) сигнала с использованием обратного БПФ кросс-спектра.

20. Определяют время прихода сигнала как аргумент максимума ДККФ сигнала.

Покажем, что в предложенном способе измерения времени прихода сигнала с М-позиционной квадратурной амплитудной манипуляцией (М=2ⁿ, где n=1, 2, … произвольное целое число большее или равное единице) возможно исключение необходимости двумерного поиска при нахождении аргумента максимума ДККФ.

Сигнал М-позиционной квадратурной амплитудной манипуляцией описывается следующим образом [24]:

где ℜ{} - оператор получения действительной части комплексного числа, A_k и θ_k - значение модулирующего символа из М-ичного сигнального множества на k-том интервале времени, ϕ_c(t)=ω_ct+ϕ₀ - фаза несущей, p(t) - прямоугольный импульс с единичной амплитудой длительностью T, определенный на интервале [-T/2, T/2], а ω_c - частота несущей.

При этом каждый k-тый символ сигнала можно представить в виде [24]

где индексом i обозначен номер символа из М-ичного сигнального множества, а

A_i1=A_icosθ_i,

A_i2=A_isinθ_i,

Символы сигнала с QAM могут быть выражены в виде линейной комбинации двух ортонормальных функций [24]

s_i(t)=s_i1Ф₁(t)+s_i2Ф₂(t),

где E_p - энергия импульса p(t) на интервале его определения. То есть , а коэффициент необходим для нормировки базисных функций Ф₁(t) и Ф₂(t). Фазовый вектор сигнала с QAM имеет вид

его длина, равная

связана с амплитудой сигнала

Таким образом, фазовый вектор s_i сигнала с QAM полностью описывает множество его символов. При этом фаза ϑ_i, равная углу поворота фазового вектора относительно оси Ф₁(t) и соответствующая паре A_i и θ_i значений модулирующего символа из М-ичного сигнального множества, имеет вид

С учетом (1)-(3) полную фазу сигнала с М-позиционной квадратурной амплитудной манипуляцией можно выразить как

При квадратурном разложении сигнала (1), несущая частота которого априорно неизвестна в полной фазе сигнала, практически всегда будет частотная расстройка между частотой несущей сигнала ω_c и номинальной частотой ω₀, относительно которой осуществляется квадратурное разложение, то есть в полной фазе сигнала будет присутствовать компонента, линейно зависящая от времени, которая соответствует второму слагаемому выражения (3), что не позволяет напрямую использовать выражение для полной фазы для формирования ДККФ.

На фиг.1 представлен пример полной фазы сигнала с 16-позиционной QAM при наличии частотной расстройки, демонстрирующий влияние компоненты, линейно зависящей от времени.

Из представленного на фиг.1 примера видно, что при наличии частотной расстройки полная фаза сигнала не тождественна модулирующей функции сигнала, и ее нельзя напрямую использовать для одномерной корреляционной обработки при определении времени прихода сигнала.

Разность полных фаз сигнала со сдвигом на длительность символа T позволяет исключить частотную расстройку, как компоненту, линейно зависящую от времени (см. фиг.2)

Как видно из выражения (5), разность фаз Ψ(t), за исключением постоянного смещения ω₀Т, определяемого величиной частотной расстройки, однозначно связана с модулирующей функцией сигнала.

Поскольку постоянное смещение не влияет на аргумент кросс-корреляционной функции [19], то одномерная корреляционная обработка разностной модулирующей функции сигнала (сформированной так же, как и разность фаз Ψ(t)) с функцией разности фаз сигнала Ψ(t), позволит определить время прихода сигнала как аргумент максимума кросс-корреляционной функции указанных сигналов.

Согласно второму варианту предлагаемого способа, исключающему погрешность измерений, вызываемой некратностыо длительности модулирующего символа сигнала и частоты выборки аналого-цифрового преобразования принятого сигнала:

1. Принимают сигнал.

2. Преобразуют принятый сигнал в первый цифровой поток данных, представляющий сигнал как ряд значений функции времени, преобразованных в цифровую форму.

3. Осуществляют квадратурное разложение первого цифрового потока данных относительно номинальной центральной частоты модулированного сигнала в соответствующее указанному потоку множество синфазных и квадратурных отсчетов.

4. Полученные синфазные и квадратурные отсчеты независимо низкочастотно фильтруют с частотой среза, соответствующей скорости манипуляции модулирующего сигнала, деленной на n.

5. Отфильтрованные синфазные и квадратурные отсчеты дополнительно децимируют и интерполируют с обеспечением кратности частоты отсчетов первого цифрового потока данных длительности символа сигнала.

6. Получают множество текущих фаз сигнала, как аргументов комплексных чисел, в качестве действительной части которых используют соответствующие синфазные отсчеты, а в качестве мнимой - соответствующие квадратурные отсчеты сигнала.

7. Задерживают множество полученных текущих фаз сигнала на длительность символа модулирующего сигнала.

8. Вычитают по модулю 2π из каждой полученной текущей фазы соответствующее значение задержанной текущей фазы сигнала.

9. Преобразуют с использованием БПФ полученный разностный цифровой поток данных, как первый цифровой поток данных в дискретные значения первой функции частоты S₁(k), где k - целочисленная индексная переменная, изменяющаяся в пределах длины данных.

10. Исходное битовое сообщение последовательно-параллельно разделяют на синфазный битовый сигнал и квадратурный битовый сигнал.

11. Из синфазного битового сигнала последовательно-параллельным преобразованием с разрядностью 2^n-1 формируют синфазный многоуровневый сигнал.

12. Из квадратурного битового сигнала последовательно-параллельным преобразованием с разрядностью 2^n-1 формируют квадратурный многоуровневый сигнал.

13. Полученный квадратурный многоуровневый сигнал делят на синфазный многоуровневый сигнал.

14. От результата деления находят функцию арктангенса.

15. Сформированный арктангенсный сигнал задерживают на длительность символа.

16. Вычитают по модулю 2π из сформированного сигнала задержанный сигнал.

17. Отображают каждый символ полученного разностного сигнала на соответствующее количество отсчетов преобразованного в цифровую форму принятого сигнала относительно шкалы времени приемной позиции и формируют, таким образом, второй цифровой поток данных.

18. Преобразуют с использованием БПФ упомянутый второй цифровой поток данных в значения второго спектра, который представляет сигнал как ряд значений функции частоты S₂(k).

19. Взаимно перемножают значения спектра одного из сигналов с комплексно сопряженными значениями спектра другого сигнала для порождения кросс-спектра.

20. Вычисляют дискретную кросс-корреляционную функцию (ДККФ) сигнала с использованием обратного БПФ кросс-спектра.

21. Определяют время прихода сигнала как аргумент максимума ДККФ сигнала.

Некратность длительности модулирующего символа сигнала и частоты выборки аналого-цифрового преобразования принятого сигнала можно устранить, к примеру, полифазной фильтрацией [18], позволяющей за счет интерполяции и децимации обеспечить целочисленное количество отсчетов сигнала на длительности символа на конечном интервале времени.

Согласно другому варианту предлагаемого способа, исключающему погрешность дискретности:

1. Принимают сигнал.

2. Преобразуют принятый сигнал в первый цифровой поток данных, представляющий сигнал как ряд значений функции времени, преобразованных в цифровую форму.

3. Осуществляют квадратурное разложение первого цифрового потока данных относительно номинальной центральной частоты модулированного сигнала в соответствующее указанному потоку множество синфазных и квадратурных отсчетов.

4. Полученные синфазные и квадратурные отсчеты независимо низкочастотно фильтруют с частотой среза, соответствующей скорости манипуляции модулирующего сигнала, деленной на n.

5. Получают множество текущих фаз сигнала как аргументов комплексных чисел, в качестве действительной части которых используют соответствующие отфильтрованные синфазные отсчеты, а в качестве мнимой - соответствующие отфильтрованные квадратурные отсчеты сигнала.

6. Задерживают множество полученных текущих фаз сигнала на длительность символа модулирующего сигнала.

7. Вычитают по модулю 2π из каждой полученной текущей фазы соответствующее значение задержанной текущей фазы сигнала.

8. Преобразуют с использованием БПФ полученный разностный цифровой поток данных как первый цифровой поток данных в дискретные значения первой функции частоты S₁(k), где k - целочисленная индексная переменная, изменяющаяся в пределах длины данных.

9. Исходное битовое сообщение последовательно-параллельно разделяют на синфазный битовый сигнал и квадратурный битовый сигнал.

10. Из синфазного битового сигнала последовательно-параллельным преобразованием с разрядностью 2^n-1 формируют синфазный многоуровневый сигнал.

11. Из квадратурного битового сигнала последовательно-параллельным преобразованием с разрядностью 2^n-1 формируют квадратурный многоуровневый сигнал.

12. Полученный квадратурный многоуровневый сигнал делят на синфазный многоуровневый сигнал.

13. От результата деления находят функцию арктангенса.

14. Сформированный арктангенсный сигнал задерживают на длительность символа.

15. Вычитают по модулю 2π из сформированного сигнала задержанный сигнал.

16. Отображают каждый символ полученного разностного сигнала на соответствующее количество отсчетов преобразованного в цифровую форму принятого сигнала относительно шкалы времени приемной позиции и формируют, таким образом, второй цифровой поток данных.

17. Преобразуют с использованием БПФ упомянутый второй цифровой поток данных в значения второго спектра, который представляет сигнал как ряд значений функции частоты S₂(k).

18. Взаимно перемножают значения спектра одного из сигналов с комплексно сопряженными значениями спектра другого сигнала для порождения кросс-спектра.

19. Вычисляют ДККФ сигнала с использованием обратного БПФ кросс-спектра.

20. Определяют время прихода сигнала, как аргумент максимума ДККФ сигнала.

21. Слева и справа от аргумента максимума ДККФ сигнала выбирают по L точек указанной функции.

22. Значения ДККФ для выбранных точек и точки максимума объединяют в порядке временного следования в вектор-столбец с.

23. Из единиц формируют вектор-столбец v₀ такой же размерности, как вектор с.

24. Соответствующие выбранным точкам ДККФ аргументы выражают через индексную переменную l=0, ±1, …, ±L, где индексы l с отрицательным знаком соответствуют временам до точки максимума ДККФ, нулевой индекс l соответствует точке максимума ДККФ, а индексы l с положительным знаком соответствуют временам после точки максимума ДККФ.

25. Аргументы выбранных точек ДККФ упорядочивают также, как и компоненты вектора с, и объединяют в вектор-столбец v₁.

26. Квадраты компонент вектора v₁ аналогично объединяют в вектор-столбец v₂.

27. Определяют по следующему правилу уточненное значение ВП

где N=2L+1 - размерность сформированных векторов, надстрочный индекс ^T обозначает операцию транспонирования вектора, T_s - период дискретизации сигнала, - скалярное произведение векторов v₁ и с, коэффициент Р определяется выражением

коэффициент Q определяется другим выражением

а (NPv₂-P²v₀)^Tc - скалярное произведение разностного вектора (NPv₂-P²v₀) с вектором с.

При цифровом преобразовании непрерывного сигнала неизбежно появляются погрешности дискретности [17-18], их влияние может быть существенно снижено интерполяцией ДККФ в окрестности экстремума, что не влечет значительных вычислительных затрат, возникающих при интерполяции сигнала в целом.

Вариант предлагаемого способа, исключающий погрешность дискретности при оценке параметров дискретной кросс-корреляционной функции основан на том, что в окрестности максимума указанная функция имеет форму параболы [13, стр.8-9], оценив параметры которой в результате решения системы линейных уравнений, можно уточнить значение времени прихода как аргумента максимума ДККФ, поскольку ДККФ является выборочной от кросс-корреляционной функции в непрерывном времени.

Уравнение, описывающее вершину кросс-корреляционной функции C_XY(τ) как параболу, имеет вид

Для заданных отсчетов с_n кросс-корреляционной функции C_XY(τ)

где ξ_n - погрешность задания отсчетов КФ, T_s - период дискретизации.

Для параболы (6) оценка точки экстремума (в данном случае максимума, исходя из смысла задачи и предположения о единственности экстремума в рассматриваемой окрестности) определяется соотношением

Оценки для коэффициентов a, b в (8) могут быть получены из линейной системы вида

где ξ - вектор погрешностей задания отсчетов кросс-корреляционной функции (7). Кроме того, в (9) предполагается нечетное число исходных данных (7) и принята симметричная индексация n=-K, -(K-1), …, -1, 0, 1, 2, …, K, и хотя данные предположения не существенны для общей оценки по методу наименьших квадратов (МНК), они не умаляют общность, а их смысл будет пояснен позднее.

Согласно [22] МНК оценка вектора коэффициентов для (9) и соответствующая (8) оценка задержки имеют вид

где V^† - псевдообратная матрица, которая при существовании W=(V^TV)^-1 имеет вид V^†=WV^T [22-23]. Приняв оценку , определяемую в (8) за требуемое решение, заметим, что для ее получения в указанном виде должна быть использована операция обращения матрицы, что не всегда вычислительно эффективно, особенно при реализации слежения за задержкой в реальном времени. Матрица V^† не зависит от исходных измерений (7) и может быть рассчитана априорно, но она зависит от объема данных N. При таком подходе необходимо хранить набор матриц для различных N, либо требовать работы с всегда фиксированным объемом, что тоже может оказаться не оптимальным. Кроме того, при вычислении оценки согласно первому выражению в (10) осуществляются затраты на оценку , не используемую далее. С целью повышения вычислительной эффективности получим для величины