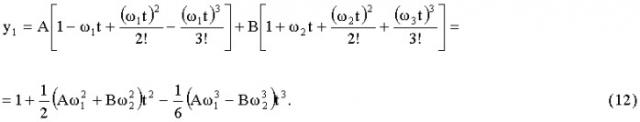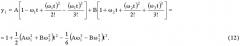Способ повышения надежности изделий (варианты)

Способ повышения надежности изделий (варианты)

Иллюстрации

Показать все

Реферат

Изобретение относится к области машиностроения и авиационно-космической техники и может быть использовано при создании различного класса изделий.

Порядок создания, производства и эксплуатации изделий, в том числе космических комплексов, регламентируется соответствующими нормативными документами и ГОСТами. Основным показателем качества изделия является надежность - свойство изделия сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортирования. Надежность является сложным свойством и состоит из сочетаний свойств, в частности безотказности и долговечности (ГОСТ 27.002.89 «Надежность в технике»).

Существующий способ обеспечения, повышения надежности изделий включает определение интенсивности отказов, длительности функционирования, устранение дефектов и совершенствование изделий и их составных частей. Комплекс взаимосвязанных требований и мероприятий, направленных на выполнение заданных в документации на изделие требований по надежности на соответствующей стадии жизненного цикла, представлен в ГОСТах (ГОСТ 27.410.87 - «Методы контроля показателя надежности и плана контрольных испытаний» и др.) и дан в справочнике Ю.К.Беляев, В.А.Богатырев и др. «Надежность технических систем», М.: Радио и связь, 1985 г. Указанный способ обладает существенным недостатком, а именно эволюционным характером совершенствования изделия, определяемым естественными причинами, особенно в ракетно-космической технике (РКТ), такими как уникальность изделия, малая серия или единичные экземпляры, продолжительность создания (отработки) и его высокая стоимость. Все это ограничивает возможности принятия решений по использованию ряда мероприятий, направленных на совершенствование изделий, в том числе и инновационных.

Известен способ повышения надежности, включающий структурные и физические методы расчета (определения) количественных показателей надежности (безотказности, долговечности) и выбора оптимальных технических решений по совершенствованию изделий (составных частей). Основные положения этого способа изложены в монографии: В.Ф.Грибанов, А.И.Рембеза и др. «Методы отработки ракетно-космических комплексов», М.: Машиностроение, 1995 г. Однако этот способ (аналог) является трудоемким и, кроме того, сам выбор статистических распределений отказов не имеет обоснований. Это приводит к использованию различных распределений не только на отдельных этапах жизненного цикла, но и самих изделий и значительно усложняет поиск решений по повышению надежности изделий. Предлагаемый способ устраняет недостатки существующих способов (аналогов) и направлен на повышение надежности изделий.

Сущность предлагаемого способа заключается в следующем.

Способ повышения надежности изделий, включающий определение зависимости интенсивности отказов δ от определяющих характеристик (параметров) изделия, длительности функционирования t, устранение дефектов, совершенствование изделия и его составляющих элементов, повышающее их отказоустойчивость, ресурс, отличается тем, что дополнительно вводят в качестве определяющего параметра ускорение (торможение) интенсивности отказов G и устанавливают расчетно-экспериментальным путем взаимосвязь между параметрами согласно функционалу:

δ=f(δ₀, α, β, t),

где δ₀ - начальное значение интенсивности отказов,

, - параметры, обратные величинам скорости и ускорению интенсивности отказов соответственно; нормируют параметры изделия по интенсивности отказов в цикле испытаний, затем прогнозируют интенсивность отказов на заданное время (цикл) и совершенствуют изделие, его элементы изменением их параметров, приводящее к повышению отказоустойчивости, ресурса. При этом определяют дифференциальные и интегральные зависимости интенсивности отказов в апериодическом и колебательном (циклическом) процессах изменения параметров изделия. Кроме того, определяют экспериментальным путем частотно-временной спектр отказов в этих процессах, а нормирование параметров изделия, его элементов осуществляют по динамике изменения целевых функций (значений скорости, ускорения) от воздействия внутренних физических факторов (параметров): электрических, тепловых, механических и внешних: ионизирующих излучений космического пространства, электризация. При этом отказы изделия, его элементов отождествляют с их частотно-амплитудными функционалами, как при воздействии отдельных факторов, так и комплексное их воздействие. Прогнозирование и повышение ресурса осуществляют изменением параметров изделия согласно найденных амплитудно-частотных характеристик отказов в рассматриваемых процессах (стадиях) отработки изделия. При этом повышение ресурса осуществляют ступенчатым процессом, циклическим в начале, и последующей апериодической стадией, а смена стадий происходит с момента времени, удовлетворяющего условию t>t^∗, где t^* - граничное значение, с линейной зависимостью приращения ресурса на начальной стадии и нелинейной зависимостью приращения ресурса на апериодической стадии.

В обоснование способа рассмотрим модель изменения (сохранения) количества изделий в группе с одинаковыми свойствами (характеристиками). Это изменение может происходить как за счет отказов при функционировании, так и при восполнении группы. Предположим, что это изменение осуществляется по нелинейному закону и может быть представлено уравнением вида:

где , - производные «y» по времени,

α, β - коэффициенты пропорциональности (обратные величины скорости и ускорения изменения величин «y»).

Решение уравнения (1) представим в виде y=e^ωt, для которого найдем равенство:

Корнями этого уравнения являются зависимости:

при β≠0 и .

Тогда решением уравнения (1) является функция:

где ,

,

A, B - константы.

Константы определяем из начальных условий:

(при нормировании «y» на единицу при , где y₀ - начальное значение числа изделий в группе), для которых получим следующие равенства:

1)

2)

Отсюда найдем константы A и B:

и

Подставив соответствующие значения, получим:

Рассмотрим некоторые особенности решения (4), используя значения констант (9). Можно видеть, что при γ>1 имеем непрерывно возрастающее значение y₁→ ∞ при t→ ∞.

При γ=1 константы принимают значения A=0, B=1 и решение постоянно во времени (y₁=1).

В диапазоне значений 1>γ>0 константы A и B могут принимать большие значения, при этом величины A и ω₂ становятся отрицательными. Этот случай характеризуется тем, что при некоторых параметрах значение y₁ может принимать как нулевые, так и положительные, и отрицательные значения. Определим границу изменения знака функции (4) при y₁=0:

отсюда

A+Bexp(ω₂+ω₁)t=0, (т.к. и A<0)

найдем и решением является функция:

Это уравнение становится определенным в 2^x случаях:

1) β<0 (β_- - модуль) при α>0;

2) β>0 и α<0 (α_- - модуль).

Далее рассматриваем решение (4) с константами (9). Разложив функции выражения (4) в ряд, найдем:

Подставив соответствующие значения в (12) и проведя преобразования, получим:

а при γ>>1 имеем:

В диапазоне 0<γ<1, приняв γ<<1 и учитывая, что этот вариант характерен при β<0 (β_- - модуль) при α>0, то решение (13) имеет вид:

Для β>0 и α<0 (α_{-_} - модуль) имеем то же уравнение:

Рассмотрим решение уравнения (1) при отрицательном детерминанте (3), т.е. при γ<0, для которого β<0 (β_- - модуль) и

Общим решением этого уравнения будет функция:

Константы в выражении (17) определяем, как и ранее из условий (6, 7), из которых получим B=1, . Тогда уравнение (17) запишется в виде:

Обозначим , где и, подставив эти значения в (18), оно приводится к следующему виду:

Рассмотрим выражение (19) - его тригонометрическую часть:

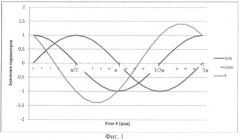
На фиг.1 приведена зависимость F от x₁ при γ=1 в одном периоде. Можно видеть, что в одном периоде функция F положительна в диапазоне , а в диапазоне она отрицательна.

Характерными особыми точками являются и , при которых происходит изменение знака функции.

При значении и наблюдается максимум функции (по модулю).

Разложим функцию F в ряд вблизи особой точки , заменив , и tgx₁=x₁≤1, найдем

которая учитывает особенности ее изменения при определенных параметрах. Разложив exp в ряд и подставив значение F (20) выражение (19) принимает вид:

При этом в выражение (21) введен нормировочный множитель так, чтобы при x₁→0, y₂→1.

По найденным значениям P_1,2=y_1,2 найдем относительную долю отказов согласно соотношению:

где коэффициент δ₀ является нормированным множителем, определенным принципом соответствия теоретических расчетов экспериментальным значениям вблизи начальных значений. Согласно (22) и соответствующих значений (13) и (21) относительная доля отказов в «апериодическом» режиме описывается соотношением

где , , а

в «колебательном» режиме соотношением

где ,

Можно видеть, что выражения F_1,2 представляют собой зависимость относительной доли отказов от частотно-временных параметров x, z и величины γ. По аналогии с атомной физикой об излучении возбужденного атома, сопровождающего переход атома из состояния n в состояние m, согласно бальмеровской формуле hν=E_n-E_m, где E_n, E_m - энергия атома в состоянии n, m; h - постоянная Планка, ν - частота излучения. Можно представить, что отказ - это тоже «излучение», обусловленное переходом системы изделий из одного состояния в другое (М.Борн «Атомная физика» Москва, Мир, 1965 г.). При таком подходе положительные значения F_1,2 - это «излучение» с определенным спектром, а при отрицательных значениях - «поглощение», эквивалентное восстановлению устойчивого состояния системы изделий.

При таком предположении из выражений (23), (24) можно выделить характерные спектры «излучения», характеризующиеся целочисленными значениями частот при параметрах, зависящих от интервала времени между этими «излучениями» (отказами).

Так в (23) можно выделить спектр частот:

ν₁=nν₀,

где , n-=1, 2, 3, … при значениях параметра x≤1÷ и спектр частот , где m=1, 2, 3, … при x≤1÷.

Согласно выражению (24) спектр частот определяется выражением ν₃=ν_1оk,

где k=1, 2, 3, …

и значении z≤1 , а также близкое к ν₁, где l=1, 2, 3, … и .

Определяем особенности зависимостей (23), (24) при непрерывном изменении параметров. Найдем экстремумы, приравняв к нулю их производные:

При γ≠1 корнями уравнения являются x=0 и x=1.

Значение функции (23) при x=1 и γ<<1 равно F₁=1/6.

В диапазоне 0<x<3/2 при γ<1 излучение принимает максимальное значение, так что F₁=1/6 вблизи x=1.

При γ>>1 «излучение» происходит при x<3/2 и быстро растет с увеличением x.

В диапазоне значений γ<1 динамику отказов при x< определяет параметр γ, тогда как при γ>1 и x> динамику отказов определяет в основном x при существенном влиянии на излучение и величины γ, пропорциональной γ². Найдем оптимум выражения (24) при

Обозначив получим или

Корнями этого уравнения являются выражения:

или

В таблице приведены максимальные значения F₂ (24) при положительном корне z₁ и различных γ₁:

γ1	z1	1-z1		1-		1-	(1-z1)	F2
1	1,00	0,00	1,00	0,00	2,00	0,00	0,00	1,00
1/2	0,77	0,23	1,55	-0,55	2,55	-1,40	-0,32	1,32
1/3	0,72	0,28	2,15	-1,15	3,15	-3,64	-1,03	2,03
1/4	0,70	0,30	2,79	-1,79	3,79	-6,76	-2,05	3,05
1/9	0,67	0,33	6,06	-5,06	7,06	-35,66	-11,67	12,67
3/2	1,26	-0,26	0,84	0,16	1,84	0,29	-0,08	1,08
2	1,54	-0,54	0,77	0,23	1,77	0,41	-0,22	1,22
3	2,10	-1,10	0,70	0,30	1,70	0,51	-0,56	1,56
4	2,67	-1,67	0,67	0,33	1,67	0,56	-0,93	1,93
5	3,24	-2,24	0,65	0,35	1,65	0,58	-1,30	2,30
10	6,12	-5,12	0,61	0,39	1,61	0,63	-3,20	4,20

Из таблицы видно, что максимальная доля отказов («излучение») становится значительной в различных диапазонах частотно-временного интервала. Так, в одном диапазоне параметров 0<γ₁≤1 z₁ изменяется незначительно и лежит в диапазоне 1≥z≥ а интенсивность отказов (F₂) лежит в диапазоне (1÷3) и лишь при γ≤0,1 интенсивность быстро растет. В этом диапазоне параметров величину отказов определяет величина γ₁, т.е. отношение z₁/γ₁.

При параметрах γ₁≥1 динамику отказов определяет величина z₁, тогда как отношение ~0,6÷1 изменяется слабо.

Из динамики изменения отказов от параметров можно утверждать и обратное - частотно-временные параметры определяются интенсивностью отказов. Так, согласно (23) и (24) предельные значения параметров достигают при δ_1,2-δ₀=F_1,2δ₀≤1. Это обстоятельство дает возможность нормировать введенные параметры по уровню отказов (их скорости, ускорению) в течение определенного времени.

Так, для состояния системы, описываемой выражением (23) при γ_-<<1 и x< производные равны:

Положив, для примера, и γ_-=1,

найдем . Отсюда получим α=1 и , при которых интервал времени равен t=1 (в относительных единицах).

Таким образом, найденные выражения (23) и (24) позволяют по динамике изменения отказов во времени, определяемой экспериментальным путем, проанализировать введенные динамические параметры группы изделий. Знание этих параметров позволяет по найденным функциональным связям прогнозировать поведение группы изделий во времени и совершенствовать изделие (повышение отказоустойчивости, увеличение ресурса) с учетом изменения этих параметров, т.е. позволяет управлять процессом совершенствования изделия. Поскольку комплексные испытания изделия на отказоустойчивость (ресурс) - процесс длительный и дорогостоящий, то нормирование введенных показателей предлагается осуществлять на других этапах жизненного цикла изделия и его составных частей, в частности на этапах проектных разработок и автономных испытаний по динамике изменения (скорости, ускорения) целевых функций (параметров) изделия (составных частей) при действии различных факторов, как внутренних: электрических, тепловых, механических и др., а также их комплексное воздействие, так и внешних факторов: ионизирующих излучений космического пространства, электризации и др.

Из выражений (23) и (24) видно, что путем простого смещения

переменных величин x, z функции F₁, F₂ повторяются вместе со значениями δ₀, т.е. уравнение и решение инвариантны к смещению координат на постоянную величину. Учитывая это обстоятельство, для простоты анализа и прогнозирования изменения параметров указанные выражения преобразуем к дифференциальному виду:

приняв при этом и

, где .

Как видно из выражения (30), направление процесса отказов (знак производной) зависит от γ². В дальнейшем, с практической точки зрения, будем рассматривать только затухающие решения, поэтому используем модуль выражения |γ²-1|.

Интегрирование выражения (30) при условии x₁=0, δ=0 дает зависимость

а при условии х₁=0, δ=δ_max=δ_m эта зависимость имеет вид:

В общем случае множитель в экспоненте выражения (31), (32) в силу сделанных допущений может быть величиной a≤1, определяемый экспериментальным путем. При этом показатель степени в экспоненте может лежать в диапазоне 2<к≤4.

Аналогичные частные решения получаем из выражения (24).

Так, после простых преобразований при функция F₂ после подстановки соответствующих значений приводится к виду:

где

,

положив при этом и 1-z=Δz→dz=γ_-dx_- (т.к. ).

Решением уравнения (33) при x_>1 с начальными условиями δ=0 при x_-=0 является выражение

а с начальными условиями: δ=δ_m, x_-=0 является выражение

При функция F₂ приводится к виду

где (, ), полученному путем упрощающихся допущений:

при 1-y=Δy→dy и 1+y≈1,7 (см. таблицу) и γ₁y>1.

Частным решением уравнения (36) является функция

с начальными условиями: δ=0 при x_-=0 и ()

и

при δ=δ_m, x_-=0.

В общем случае коэффициент в экспоненте может принимать значения a₂≤1, а показатель степени в экспоненте принимать значения, лежащие в диапазоне 1≤n≤4, уточняемый с учетом сделанных допущений в эксперименте. Найденные распределения (31, 32, 34, 35, 37, 38) дают интегральную временную зависимость отказов от частоты и параметра γ₁ при «апериодическом», «колебательном» (циклическом) процессах изменения состояния системы изделий. По этим зависимостям возможно оценить (прогнозировать) ресурс (срок активного существования (САС)) изделия, группы изделий, определяемый как предельное значение времени, когда все (почти все) элементы группы выйдут из работоспособного состояния.

Так, положив, что в начальный момент времени система характеризовалась максимальным уровнем отказов, то ко времени уровень отказов должен быть минимальным δ=δ_min (задаваемый уровень). Его можно оценить по найденным выражениям в наиболее удобном их представлении. Так, прологарифмировав выражение (32) и извлекая корень, получим:

Подставив значения δ_max/δ_min=3; 10³ и a₀=1; 0,1 (при n=3), найдем, что правая часть выражения (39) равна 1; 1,9 (для a₀=1) и во втором случае - 2,1 и 4 соответственно (для a₀=0,1), т.е. она изменяется лишь на несколько единиц при изменении δ_max/δ_min на три порядка величины, а коэффициент a₀ на порядок. Поэтому можно принять, что функционал

где 2<n≤4, константа к принимает значения, лежащие в диапазоне 1≤к≤10, инвариантен по отношению к отказам и других причин, определяемых коэффициентом a₀. При этом константа к и коэффициент a₀ могут быть определены экспериментальным или расчетно-теоретическим путем при нормировании параметров. В этом случае выражение (40) является уравнением состояния (уравнением процесса), определяющим взаимосвязь ресурса с динамическими параметрами системы для апериодического процесса совершенствования изделия, определяемыми их начальными и конечными значениями в этом процессе. Указанный процесс аналогичен известным термодинамическим процессам в газовой динамике с их определяющими параметрами. Аналогичные уравнения состояния системы получаем из выражений (35) и (38) для колебательного (циклического) процесса совершенствования изделия (группы изделий) в виде:

при ,

и

при .

Значения констант в выражениях (41) и (42), так же как в выражении (39), практически не зависят от условий. Так, при δ_max/δ_min=3; 10³ и a₁=0,1 и фиксированном показателе степени согласно (41) константа лежит в диапазоне ~2,1÷4, а согласно (42) она лежит в диапазоне ~1,7÷4,5 при a₂=0,3. Объединяя выражения (41), (42) в общем виде для колебательного процесса, можно записать (43) при γ_->0, где лежит в диапазоне 1≤n≤4, а константа принимает значения, лежащие в диапазоне 1≤к₂≤10.

Характерной особенностью уравнений процессов (40, 41, 42) является то, что T_CAC в основном определяется частотой отказов («излучения»), а не их амплитудным значением. Эта особенность аналогична фотоэффекту - процессу, приводящему к эмиссии электронов при взаимодействии частиц (квантов электромагнитного излучения) с веществом, при котором эмиссия определяется только энергией частиц (квантов), характеризуемой их частотой, и возможна при энергии выше порогового значения (Физическая энциклопедия, т.2, М., Советская энциклопедия, 1990 г.).

В рассматриваемом случае предельным значением «излучения» является величина δ_max/δ_min→1, при которой пороговое значение в отличие от фотоэффекта для «излучения» (отказов) практически отсутствует и «излучение» возможно при любых δ_max/δ_min>1.

Представляет интерес оценить продолжительность времени, необходимого для получения приращения ресурса. Такую зависимость можно получить из дифференциальных выражений (30), (33), (36а), если перейти к частным производным, введя при этом скорость изменения от текущего времени (t) и ресурса (ν_c) в виде , где .

Тогда, определив на начальном этапе значение и полагая константу постоянной величиной, указанные уравнения позволяют определить приращение CAC (ΔT_CAC) за текущий интервал времени.

Так, из уравнения (36a), ограничившись первым членом правой части уравнения, найдем

Отсюда приращение T_CAC, равное:

линейно растет со временем.

Так, при k=1, t₀=2 года найдем, что прирост ресурса составит ΔT_CAC=1 год за 4 года.

Из выражения (36a) видно, что скорость роста ресурса (ν_c) является квадратичной зависимостью с наличием экстремума в точке , в которой скорость ν_c принимает максимальное значение

, где

Аналогичную линейную зависимость от времени T_CAC получаем по выражению (33), для которого скорость равна при . Нелинейный рост скорости ν_c (квадратичный) по выражению (30) позволит обеспечить значительный прирост ресурса при x₁>1, тогда как при x₁<1 этот прирост из-за нелинейности незначительный. Поэтому прирост ресурса в колебательном (циклическом) процессе более значителен, чем в апериодическом процессе при . С увеличением более эффективным становится апериодический процесс. В связи с изложенным, оптимальным процессом для повышения ресурса является ступенчатый процесс с линейным (от времени) приростом ресурса на первых циклах колебательного процесса с последующим ускорением прироста в апериодическом процессе.

Таким образом, предложенный способ позволяет управлять процессом совершенствования изделий на всех этапах жизненного цикла.

Технико-экономическая эффективность способа заключается в существенном сокращении продолжительности разработки (отработки) изделия и широком использовании информационных технологий в процессе создания изделия и возможности его отработки уже на этапах проектных разработок и автономных испытаний.

1. Способ повышения надежности изделий, включающий определение зависимости интенсивности отказов δ от определяющих характеристик, параметров изделия, длительности функционирования t, устранение дефектов, совершенствование изделия и его составляющих элементов, повышающее их отказоустойчивость, ресурс, отличающийся тем, что дополнительно вводят в качестве определяющего параметра ускорение требуемой функции G и устанавливают расчетным или расчетно-экспериментальным путем взаимосвязь между параметрами согласно функционалу:δ=f(δ₀, α, β, t),где δ₀ - начальное значение интенсивности отказов, , - параметры, обратные величинам скорости и ускорению требуемой функции изделия, его составных частей соответственно; нормируют параметры изделия по интенсивности отказов в цикле испытаний, затем прогнозируют интенсивность отказов на заданное время, цикл и совершенствуют изделие, его элементы изменением их параметров, приводящее к повышению отказоустойчивости, ресурса.

2. Способ повышения надежности изделий по п.1, отличающийся тем, что устанавливают взаимосвязь между параметрами изделия, при изменении требуемой функции согласно выражению: а интегральное распределение отказов определяется зависимостью:δ=δ₀exp[-a|γ²-1|xⁿ]илиδ=1-exp[-a|ν²-1|xⁿ],где обозначено: , ,t - время, , ν=1/t₀ - характерная частота,δ, δ₀ - величина отказов - текущая и в начале процесса соответственно;или согласно выражению: а интегральное распределение отказов определяется зависимостью или где β- - модуль β<0;n, k - показатели степеней, лежащих в диапазоне 1≤n, k≤4;a, a₁≤l - коэффициенты пропорциональности.

3. Способ повышения надежности изделий по п.1 или 2, отличающийся тем, что нормирование параметров изделия, его элементов осуществляют по динамике изменения требуемых функций, их значений скорости, ускорения от воздействия внутренних физических факторов: электрических, тепловых, механических и внешних: ионизирующих излучений космического пространства, электризации, при этом отказы изделия, его элементов ставят в соответствие с частотно-амплитудными функционалами требуемой функции, как при воздействии отдельных факторов, так и комплексного их воздействия.

4. Способ повышения надежности изделий, включающий определение зависимости интенсивности отказов δ от определяющих характеристик, параметров изделия, длительности функционирования t, устранение дефектов, совершенствование изделия и его составляющих элементов, повышающее их отказоустойчивость, ресурс, отличающийся тем, что прогнозирование и повышение ресурса осуществляют изменением параметров изделия согласно динамике изменения частотно-амплитудных характеристик требуемой функции и распределения отказов в процессе, стадии отработки изделия, его элементов.

5. Способ повышения надежности изделий по п.4, отличающийся тем, что прогнозирование и повышение ресурса осуществляют расчетным или расчетно-экспериментальным методом согласно выражению: , с момента времени, удовлетворяющего условию t>t*,где , T_cac - срок активного существования, γ≠1,или согласно выражению при t≤t*, γ_->0, где показатели степени n, k лежат в диапазоне 1≤n≤4, а коэффициенты пропорциональности K_1,2 принимают значения, лежащие в диапазоне 1≤K_1,2≤10.