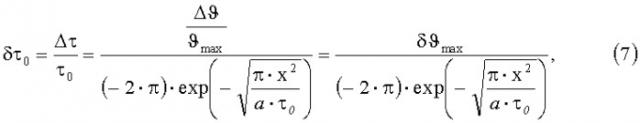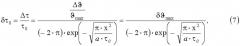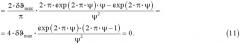Способ измерения коэффициента температуропроводности теплоизоляционных материалов методом регулярного режима третьего рода

Способ измерения коэффициента температуропроводности теплоизоляционных материалов методом регулярного режима третьего рода

Иллюстрации

Показать все

Реферат

Изобретение относится к области тепловых испытаний теплоизоляционных материалов, а именно к области исследования теплофизических характеристик этих материалов.

Известен способ определения комплекса теплофизических свойств твердых материалов [патент РФ №2374631, кл. G01N 25/18, 2008], включающий тепловое импульсное воздействие на плоскую поверхность исследуемого образца и измерение избыточной температуры на плоской поверхности образца в одной точке в заданном интервале времени. Тепловое импульсное воздействие осуществляют лучистым тепловым потоком известной плотности и длительности, а измерение избыточной температуры с момента подачи теплового импульса проводят в центральной части нагреваемой поверхности образца, при этом регистрируют значение максимальной избыточной температуры и время ее достижения.

К недостаткам этого способа относятся невысокая точность измерения коэффициента температуропроводности и необходимость наличия специальной аппаратуры (инфракрасного излучателя и инфракрасного измерителя температуры).

Известен способ измерения температуропроводности и теплоемкости горных пород методом плоских температурных волн [Зиновьев В.Е., Бочаров В.И., Мулюков P.P. и др. Прибор для автоматизированных измерений теплофизических характеристик горных пород в условиях, близких к естественным // Измерительная техника. - 1985. №1. - С.62-63], заключающийся в том, что тонкий малоинерционный нагреватель, задающий периодический нагрев, располагается между исследуемым образцом и эталонным образцом того же размера. Колебания температуры на противоположных от нагревателя поверхностях исследуемого образца и эталона регистрируются с помощью термопар.

Недостатками этого способа являются большая длительность и трудоемкость эксперимента, а также необходимость использования эталонного образца.

Наиболее близким техническим решением является способ измерения коэффициента температуропроводности методом регулярного режима третьего рода [Теоретические и практические основы теплофизических измерений: под ред. С.В.Пономарева / С.В.Пономарев, С.В.Мищенко, А.Г.Дивин, В.А.Вертоградский, А.А.Чуриков. - М.: ФИЗМАТЛИТ, 2008. - 408 с.], заключающийся в том, что в исследуемом плоском образце размещают в сечениях с координатами x=x₁ и x=x₂ два датчика температуры, выполненные в виде термопар или термометров сопротивления. Образец, покрытый сверху теплоизоляцией, помещают на поверхность элемента Пельтье, являющегося источником гармонических колебаний температуры. В процессе эксперимента на рабочую поверхность исследуемого образца подают периодическое температурное воздействие и на протяжении всей активной стадии эксперимента регистрируют температуры Т(x₁,τ) и Т(x₂,τ) в точках с координатами x=x₁ и x=x₂. О наступлении установившегося во времени регулярного режима третьего рода судят по достижению постоянных значений амплитуд гармонических колебаний. Измеряют расстояние (x₂-x₁) и, после обработки экспериментальных данных, определяют амплитуды ϑ_m(x₁) и ϑ_m(x₂) гармонических колебаний в точках с координатами x=x₁ и x=x₂ и величину времени запаздывания гармонических колебаний в точке x=x₂ по сравнению с точкой x=x₁, а искомый коэффициент температуропроводности а вычисляют по формуле где τ₀ - период гармонических колебаний.

Недостатком данного способа является невысокая точность измерения коэффициента температуропроводности исследуемого материала.

Техническая задача изобретения - повышение точности измерения коэффициента температуропроводности теплоизоляционных материалов за счет выбора оптимальных режимных параметров теплофизического эксперимента.

Техническая задача достигается тем, что в способе измерения коэффициента температуропроводности теплоизоляционных материалов методом регулярного режима третьего рода, заключающемся в том, что в изготовленном плоском образце исследуемого материала размещают в сечениях с координатами x=x₁ и x=x₂ два датчика температуры, выполненные в виде термопар или термометров сопротивления, образец, покрытый сверху теплоизоляцией, помещают на поверхность элемента Пельтье, являющегося источником гармонических колебаний температуры, на протяжении активной стадии эксперимента регистрируют температуры в двух точках исследуемого образца, измеряют расстояние (x₂-x₁), период гармонических колебаний τ₀ и время запаздывания τ_з(x₂,x₁) гармонических колебаний на глубине x=x₂ по сравнению с гармоническими колебаниями на поверхности x=x₁ образца, коэффициент температуропроводности вычисляют по формуле в отличие от прототипа, путем изменения периода τ₀ гармонических колебаний элемента Пельтье подбирают такой режим работы измерительного устройства, при котором величина отличается не более чем на малую величину ε=0,002…0,005 от заданного значения ψ_з из диапазона (0,14…0,18).

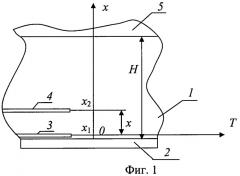
На фиг.1 представлена физическая модель устройства для осуществления метода регулярного режима третьего рода.

Исследуемый образец 7 выполнен в виде плоской пластины толщиной Н, помещенной на верхнюю поверхность источника 2 внешнего гармоничного температурного воздействия, выполненного на основе элемента Пельтье. Внутри образца в сечениях с координатами x=x₁ и x=x₂ размещены два датчика температуры 3 и 4, выполненные в виде термопар или термометров сопротивления. Для уменьшения утечек теплоты в окружающую среду верхняя поверхность образца 1 покрыта теплоизоляцией 5.

Регулярный режим третьего рода устанавливается в исследуемом образце по истечении некоторого промежутка времени после того момента, когда на поверхность этого образца начал действовать источник гармонических колебаний температуры.

Поместим начало координат по оси x в точку x=x₁, в которой установлен датчик температуры 3. Тогда точка x=x₂ в новой системе координат будет соответствовать значению x=(x₂-x₁) (см. фиг.1).

Рассмотрим процессы теплопереноса в плоском образце, на поверхности x=0 которого (где установлен датчик температуры 3) задан гармонический закон изменения температуры во времени ϑ(0,τ)=ϑ_max·cos(ω·τ).

Температурное поле во внутренних точках образца описывается выражением:

где ϑ(x,τ)=T(x,τ)-T₀ - температура исследуемого образца в точке с координатой x в момент времени τ, отсчитываемая от установившегося среднего значения температуры T₀ на поверхности исследуемого образца; T(x,τ) - температура исследуемого образца на глубине x в момент времени τ; ϑ_max - амплитуда гармонических колебаний температуры на поверхности x=0 относительно установившегося среднего значения температуры T₀ на поверхности исследуемого образца; а - коэффициент температуропроводности; τ₀ - период гармонических колебаний температур; - частота гармонических колебаний.

Задача оптимизации режимных параметров метода и конструкционного размера устройства может быть сформулирована следующим образом: для значения коэффициента температуропроводности а, например для середины диапазона исследуемого свойства a_min<а<a_max, найти такие значения периода τ₀ гармонических колебаний и геометрического размера x, чтобы погрешность определения коэффициента температуропроводности была минимальной.

Рассмотрим случай, когда коэффициент температуропроводности определяется из соотношения

где τ_з(x) - запаздывание во времени гармонических колебаний с периодом τ₀ на глубине x по сравнению с гармоническими колебаниями на поверхности x=0 образца.

Проведем оценку погрешностей измерения температуропроводности по величине сдвига фаз гармонических колебаний между двумя поверхностями x=0 и x=x образца. Основываясь на формуле (2), получим расчетное соотношение для вычисления среднеквадратичной оценки относительной погрешности δа измерения коэффициента температуропроводности.

Используя стандартную процедуру вычисления погрешностей косвенных измерений, запишем

где Δx, - абсолютная и относительная погрешности измерения расстояния между двумя поверхностями с координатами x=0 и x=x; Δτ_з, - абсолютная и относительная погрешности определения времени запаздывания τ_з; Δτ₀, - абсолютная и относительная погрешности измерения периода τ₀ колебаний.

Обозначим - отношение времени запаздывания τ_з гармонических колебаний в точке с координатой x к периоду τ₀ гармонических колебаний. Если принять, что Δτ_з=Δτ₀=Δτ, то можно представить в виде

где , - относительные погрешности измерения периода гармонических колебаний τ₀ и времени запаздывания τ_з.

Учитывая, что , получаем соотношение

позволяющее вычислить абсолютную погрешность Δτ_з(x) определения времени запаздывания на глубине x образца по известному значению абсолютной погрешности Δϑ измерения температуры ϑ(x,τ).

Продифференцировав (1), получаем

Из (5) и (6) следует, что

где принято во внимание, что ω=2·π/τ₀.

С учетом того, что наиболее благоприятные условия для измерения значения τ_з достигаются при , из (5а) следует, что

где - относительная погрешность измерения амплитуды ϑ_max гармонических колебаний температуры на поверхности х=0.

При х=0 из уравнения (7) получим

При x≠0 на основании (7) с учетом выражения (4) получаем

В формуле (9) принято во внимание, что , где φ - сдвиг по фазе между гармоническими колебаниями на поверхности x=0 и в точке с координатой x, причем . С учетом изложенного получаем, что .

Подставив (8) и (9) в (3), получаем

или

Соотношение (10) показывает, что среднеквадратичная оценка погрешности δа измерения коэффициента температуропроводности а представляет собой функцию δа=f(δx, δϑ_max, ψ), значения аргументов которой δx, δϑ_max, ψ определяются конструкцией измерительного устройства, условиями проведения эксперимента и свойствами исследуемого материала.

По полученным формулам были рассчитаны среднеквадратичные относительные погрешности для различных значений x, ψ и выбраны оптимальные параметры, обеспечивающие наименьшую погрешность измерения коэффициента температуропроводности исследуемого материала.

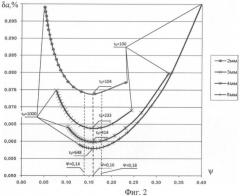
На фиг.2 показан график зависимости δа=f(ψ) для различных x (при х=2…5 мм, τ₀=100…1000 с).

При выполнении расчетов были использованы следующие значения:

а=1,2·10^-7 м²/с, x=2…5 мм, Δx=0,05 мм, Δϑ=0,1°C, ϑ_max=10°C, τ₀=100…1000 c.

Из фиг.2 видно, что для разных значений x минимумы погрешностей δа приходятся на одно и то же значение параметра ψ.

Найдем значение величины ψ, при котором достигается минимальная погрешность δа измерения коэффициента температуропроводности. Для этого воспользуемся необходимым условием экстремума функции (10) в виде уравнения

.

Принимая во внимание, что δx и δϑ_max не зависят от переменной ψ, получаем, что производная пропорциональна следующему выражению

Из уравнения (11) следует, что минимальное значение относительной погрешности δа измерения коэффициента температуропроводности достигается при (2πψ-1)=0, т.е. при ψ=1/(2π)=0,159155≈0,16. Видно, что полученная оценка величины ψ≈0,16 полностью соответствует результатам численных расчетов, проиллюстрированных на фиг.2.

Из фиг.2 видно следующее:

- минимальные значения погрешностей δа измерения коэффициента температуропроводности а достигаются при постоянном значении ψ≈0,16, но при различных значениях периода τ₀ гармонических колебаний температуры;

- допустимые значения погрешностей измерения коэффициента температуропроводности обеспечиваются при выборе заданного значения ψ_з из диапазона 0,14<ψ_з<18.

Из изложенного выше следует, что для обеспечения оптимального значения режимного параметра ψ_з процесса измерения из диапазона (0,14…0,18), в ходе эксперимента необходимо контролировать величину параметра и, за счет изменения периода τ₀ гармонических колебаний температуры, поддерживать значение разности (ψ-ψ_з)≤ε, не превышающее наперед заданную малую величину ε≈(0,002…0,005).

Способ измерения коэффициента температуропроводности теплоизоляционных материалов методом регулярного режима третьего рода, заключающийся в том, что в изготовленном плоском образце исследуемого материала размещают в сечениях с координатами x=x₁ и x=x₂ два датчика температуры, выполненные в виде термопар или термометров сопротивления, образец, покрытый сверху теплоизоляцией, помещают на поверхность элемента Пельтье, являющегося источником гармонических колебаний температуры, на протяжении активной стадии эксперимента регистрируют температуры в двух точках исследуемого образца, измеряют расстояние (x₂-x₁), период гармонических колебаний τ₀ и время запаздывания τ_з(x₂, x₁) гармонических колебаний на глубине x=x₂ по сравнению с гармоническими колебаниями на поверхности x=x₁ образца, коэффициент температуропроводности вычисляют по формуле отличающийся тем, что путем изменения периода τ₀ гармонических колебаний элемента Пельтье подбирают такой режим работы измерительного устройства, при котором величина отличается не более чем на малую величину ε=0,002…0,005 от заданного значения ψ_з из диапазона (0,14…0,18).