Широкополосная лампа бегущей волны с уменьшающимся к выводу энергии пролетным каналом

Широкополосная лампа бегущей волны с уменьшающимся к выводу энергии пролетным каналом

Иллюстрации

Показать все

Реферат

Изобретение относится к области электронных приборов СВЧ, в частности к спиральным лампам бегущей волны (ЛБВ) О-типа.

Проблема устранения самовозбуждения на обратной волне и повышения электронного КПД широкополосных спиральных ЛБВ до сих пор остается актуальной.

Известны технические решения, в которых ЛБВ содержит замедляющую систему (ЗС) типа спираль с переменным диаметром пролетного канала.

В FR 2365218 (опубл. 21.09.1976) спираль выполнена в виде усеченного конуса с непрерывным увеличением внутреннего диаметра. Диаметр увеличивается за счет преобразования круглого поперечного сечения спирали в трехгранное по направлению к выводу энергии. Поскольку крепежные диэлектрические стержни имеют постоянную высоту, внутренний диаметр спирали на участках между ними растет.

В FR 2543734 (опубл. 31.03.1983) крепежные стержни постоянной высоты предложено вставлять в желобки корпуса, глубина которых увеличивается с увеличением диаметра ЗС.

Недостатком таких технических решений является значительное снижение сопротивления связи нулевой пространственной гармоники с увеличением внутреннего диаметра ЗС, что приводит к уменьшению электронного КПД.

В [1] сказано, что проблему подавления паразитной генерации на обратной волне высоковольтных ЛБВ (с рабочим напряжением 11... 12 кВ) можно решить одновременным изменением шага и диаметра спирали. Однако ничего не говорится о том, как они должны меняться по направлению к выводу энергии - увеличиваться или уменьшаться.

В DE 3540998 (опубл. 21.05.1987) предложено иметь, по меньшей мере, два участка с различным внутренним диаметром ЗС и плавным переходом между ними. При этом не указано, какой участок стоит на выходе ЗС, у коллекторного конца, - с большим диаметром или с меньшим. Отсутствует упоминание и об изменении шага ЗС.

В WO 2004/114350А2 (опубл. 29.12.2004) с целью увеличения КПД предлагается уменьшать диаметр ЗС на выходном конце лампы бегущей волны, но отсутствуют какие-либо рекомендации по изменению шага спирали.

В US 6356022 В1 (опубл. 12.03.2002) предложено изменять на входном участке ЛБВ диаметр и, пропорционально ему, шаг ЗС типа спираль по линейному закону, причем изменение можно производить как в сторону увеличения, так и в сторону уменьшения этих параметров. При этом фазовая скорость основной гармоники остается неизменной, а изменяются только фазовые скорости остальных, нежелательных пространственных гармоник, что приводит к их подавлению. Это относится, в первую очередь, к минус первой пространственной гармонике, которая приводит к паразитному самовозбуждению ЛБВ на обратной волне. Для увеличения КПД на выходном участке ЛБВ предлагается вводить изменение шага ЗС по экспоненциальному закону, оставляя диаметр ЗС постоянным. Недостатком данного технического решения является то, что изменение диаметра ЗС осуществляется только во входной части ЛБВ, тогда как наибольшее увеличение КПД можно получить, меняя его именно в выходной части ЛБВ, одновременно подавляя при этом колебания на обратной волне.

В US 6356023 В1 (опубл. 12.03.2002), являющемся продолжением предыдущего источника, вдобавок к нему предлагается также (для повышения КПД) уменьшать затухание поглотителя, поскольку возбуждение на обратной волне будет подавлено изменением диаметра ЗС. Однако возможность этого далеко не очевидна, поскольку секционирование ЛБВ путем введения поглотителей вводится, в первую очередь, для подавления самовозбуждения на отраженной прямой волне.

Заявляемое техническое решение направлено на повышение устойчивости к самовозбуждению на обратной волне и увеличение электронного КПД взаимодействия широкополосных ЛБВ со спиральной замедляющей системой.

Технический результат в заявляемом техническом решении достигается тем, что широкополосная лампа бегущей волны (ЛБВ), содержащая замедляющую систему (ЗС) типа спираль, имеет на выходе участок, диаметр пролетного канала d (внутренний диаметр ЗС) на котором плавно или скачкообразно уменьшается по направлению к выводу энергии. При этом минимальный диаметр пролетного канала d₂ может составлять не более 0,95 от диаметра пролетного канала до начала участка d₁, то есть d₂≤0,95d₁. А на отрезке этого участка шаг спирали h₂ не должен превышать отношение диаметров до и после уменьшения, умноженное на шаг спирали h₁ до начала участка с уменьшающимся диаметром, то есть

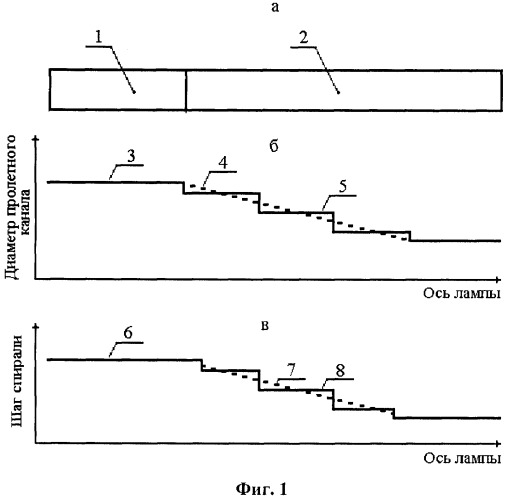
На фиг.1a представлена схема ЗС спиральной ЛБВ.

ЗС спиральной ЛБВ (фиг.1а) с начальными значениями диаметра пролетного канала и шага ЗС (1) содержит участок (2) с изменяющимися значениями этих параметров.

На фиг.1б представлено схематическое изображение изменения диаметра пролетного канала (внутреннего диаметра ЗС) вдоль длины спиральной ЛБВ.

Диаметр пролетного канала имеет постоянное (3) и уменьшающееся плавно (4) или скачкообразно (5) значение.

На фиг.1в представлено схематическое изображение ЗС спиральной ЛБВ с изменяющимся вдоль длины шагом спирали.

ЗС типа спираль (фиг.1в) имеет постоянный шаг (6) и уменьшающийся плавно (4) или скачкообразно (5) шаг вдоль длины спиральной ЛБВ.

Максимально допустимое отношение уменьшенного и начального диаметров определяется из условия, что стартовый ток в статическом режиме за счет уменьшения диаметра возрос не менее чем в 1,15 раза. Как показали проведенные в [2] расчеты, такой рост стартового тока на скачке диаметра пролетного канала происходит при отношении частот π-вида второго и первого участков, составляющем 1,05. На частоте π-вида фазовый сдвиг на шаг ЗС равен π [3]. Исходя из определения фазового сдвига [4], можно записать:

Здесь f - частота, с - скорость света в вакууме, v_ф - фазовая скорость СВЧ-сигнала, h - шаг спирали.

Заменяя с/v_ф в формуле (2) геометрическим замедлением (πd_cp/h) [4], где d_cp - средний диаметр спирали, который приближенно заменяем внутренним, найдем частоту π-вида, близкую к частоте самовозбуждения ЛБВ на минус первой пространственной гармонике f_-1

Поскольку частота самовозбуждения обратно пропорциональна диаметру пролетного канала, максимальная величина отношения диаметров второго и первого участков (d₂/d₁) при отношении частот π-вида, равном 1,05, составит 0,95. Тогда условие, которому должен удовлетворять минимальный диаметр пролетного канала d₂, запишется в виде

Здесь d₁ - диаметр пролетного канала до начала участка с уменьшающимся диаметром.

Из формулы (3) видно, что чем меньше диаметр пролетного канала d, тем больше частота самовозбуждения ЛБВ на обратной волне. Таким образом, с уменьшением диаметра пролетного канала частота самовозбуждения на обратной волне растет. И если, допустим, раньше она могла находиться в рабочей полосе частот, то уменьшением диаметра пролетного канала ее можно вывести за пределы рабочих частот и тем самым повысить устойчивость к самовозбуждению на обратной волне.

Кроме того, только уменьшение диаметра пролетного канала по направлению к выводу энергии, помимо роста сопротивления связи и обеспечения максимальной разницы фазовых скоростей минус первой пространственной гармоники (обратной волны) на участках с разными каналами, дает возможность реализовать оптимальные значения фазовых скоростей нулевой гармоники СВЧ-сигнала для получения максимального КПД. Покажем это.

Пусть есть два участка ЗС, 1 и 2, с одинаковыми шагами ЗС h и двумя разными зависимостями замедления (c/v_ф)₁ и (с/v_ф)₂ от длины волны λ (в частности, из-за разных значений диаметра пролетного канала). Обозначим замедление с/v_ф через n:

Здесь индексы 0 и -1 относятся к нулевой и минус первой пространственным гармоникам, а индексы 1 и 2 - к участкам 1 и 2.

Замедление m-й пространственной гармоники n_m определяется через замедление нулевой пространственной гармоники n₀ по формуле Релея [5]

где m - номер пространственной гармоники.

Тогда для минус первой пространственной гармоники на участках 1 и 2 можно записать

Обозначая разницу в замедлении на прямой волне на участках 1 и 2 с одинаковым шагом h как

из (7) и (7') найдем

То есть разница в замедлении на минус первой пространственной гармонике на участках 1 и 2 равна разнице замедлений на прямой волне при одном и том же шаге ЗС h на обоих участках.

Если теперь на одном из участков (например, на участке 2) изменить шаг ЗС h на h', то, считая, что в определенных пределах шаг ЗС пропорционален замедлению, можно записать

Здесь все штрихованные величины записаны для участка с измененным шагом.

Тогда разница по замедлению составит

Учитывая, что на частоте π-вида n₀=-n_-1, для нее получим

То есть разница по замедлению на обратной волне не равна разнице по замедлению на прямой волне.

Для простого случая, когда (n₀)₁=(n₀)₂ (нет разницы по замедлению на прямой волне), найдем

При изменении шага так, что

То есть разница по замедлению на прямой волне есть, а на обратной волне - нет.

Обратимся к формуле (16). Если два участка имеют разные диаметры спирали, d₁ и d₂, то при прочих равных условиях (в частности, при равных шагах), если d₂>d₁, то (n₀)₂>(n₀)₁ и Δn>0.

При уменьшении шага (h/h'>1) так, что

а при уменьшении шага (h/h'>1) так, что

Из формул (16), (22) и (22') следует, что, независимо от степени уменьшения шага, выполняется неравенство

то есть при увеличении диаметра пролетного канала (d₂>d₁) и уменьшении шага к концу ЗС разница в замедлении на прямой волне всегда больше, чем на обратной волне.

При увеличении шага (h/h'<1) так, что

а при увеличении шага (h/h'<1) так, что

Из формул (16), (22'') и (22''') следует, что, независимо от степени увеличения шага, при d₂>d₁ выполняется неравенство

то есть разница в замедлении на прямой волне всегда меньше, чем на обратной волне.

Рассмотрим случай уменьшения диаметра пролетного канала к концу ЗС (d₂<d₁). При постоянном шаге ЗС (h=h') справедливо неравенство (n₀)₂<(n₀)₁, то есть Δn<0.

При уменьшении шага на участке 2, (h/h')>1, проведя выкладки, аналогичные формулам (21)-(23), получим

то есть разница в замедлении на прямой волне всегда меньше, чем на обратной волне.

При увеличении шага на участке 2, (h/h')<1, придем к выражению

то есть разница в замедлении на прямой волне всегда больше, чем на обратной волне.

Наиболее выгодными вариантами конструкции выходной секции ЛБВ с точки зрения подавления самовозбуждения на обратной волне являются те, при которых разница в замедлении на обратной волне больше, чем на прямой волне:

1) d₂>d₁, (h/h')<1, то есть h₂>h₁,

2) d₂<d₁, (h/h')>1, то есть h₂<h₁.

Однако вариант 1 с увеличением диаметра пролетного канала к концу ЗС невыгоден, во-первых, из-за уменьшения сопротивления связи на участке увеличения диаметра, а во-вторых, из-за того, что на этом участке для повышения КПД желательно иметь увеличение замедления прямой волны, которое не реализуется при увеличении шага h₂ сверх величины (d₂/d₁)h₁. Поэтому оптимальным является вариант 2 с уменьшением диаметра пролетного канала к концу ЗС, где шаг h₂ участка с уменьшающимся диаметром удовлетворяет условию h₂≤(d₂/d₁)·h₁.

Если при уменьшении диаметра пролетного канала, d₂<d₁, выполняется условие, что (h/h')>[(n₀)₁/(n₀)₂], то разность замедлений на минус первой пространственной гармонике, согласно формуле (16), составит величину, превышающую 2Δn:

Таким образом, вариант с уменьшением диаметра к концу ЗС и уменьшением шага является наиболее устойчивым к возбуждению на обратной волне и самым оптимальным с точки зрения повышения КПД.

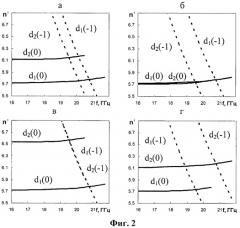
Все вышеизложенное иллюстрируется графиками, представленными на фиг.2.

На фиг.2а представлен случай постоянного шага спирали h=h₁=h₂ при увеличивающемся диаметре пролетного канала, d₂>d₁, описываемый формулой (9). На нем приведены дисперсионные характеристики (зависимости замедления n от частоты) минус первой [d₁(-1), d₂(-1)] и нулевой [d₁(0), d₂(0)] пространственных гармоник, точки пересечения которых соответствуют частотам π-вида. Видно, что замедление на участке 2 больше замедления на участке 1. На столько же разнятся замедления на минус первой пространственной гармонике при одной и той же частоте. Частоты π-вида участков 1 и 2 также различны. Все это обеспечивает повышение устойчивости ЛБВ к самовозбуждению на обратной волне.

На фиг.2б приведены дисперсионные кривые для увеличивающихся диаметра пролетного канала, d₂>d₁, и шага ЗС, h₂'>h₁, когда дисперсионные кривые нулевых пространственных гармоник для обоих каналов сливаются между собой. Этот случай описывается формулой (18). Разница замедлений на минус первой гармонике между участками 1 и 2 велика и, следовательно, устойчивость к самовозбуждению на обратной волне высокая. Но при этом дисперсионная кривая минус первой гармоники на участке 2 сдвигается в сторону меньших частот и может оказаться в рабочей полосе, что может препятствовать повышению устойчивости к самовозбуждению. Кроме того, за счет снижения сопротивления связи будет снижаться КПД. Если поменять индексы 1 и 2 на фиг.2б местами, то она будет описывать случай уменьшающихся диаметра и шага к концу ЗС. При этом из-за роста сопротивления связи возрастет КПД и устойчивость к самовозбуждению на обратной волне высокая.

На фиг.2в показаны дисперсионные кривые для увеличивающегося диаметра пролетного канала, d₂>d₁, и уменьшающегося шага ЗС, h₂'<h₁, когда дисперсионные кривые минус первой пространственной гармоники для обоих каналов сливаются между собой. Этот случай описывается формулами (19), (20). Для него никакого повышения устойчивости к самовозбуждению не произойдет, хотя скачок по замедлению на прямой волне очень большой.

На фиг.2г показаны дисперсионные кривые нулевой и минус первой пространственных гармоник (прямой и обратной волны) для уменьшающегося к концу ЗС диаметра пролетного канала, d₂<d₁, и уменьшающегося шага ЗС, h₂'<h₁, когда замедление нулевой гармоники растет. Этот случай описывается соотношением (24). Здесь различие фазовых скоростей минус первой гармоники достаточно велико, а дисперсионная кривая ее для участка 2 смещена в сторону больших частот. Все это обеспечивает высокую устойчивость к самовозбуждению на обратной волне. За счет уменьшения диаметра растет сопротивление связи, и, следовательно, КПД, который повышается также за счет увеличения замедления прямой волны к концу ЗС.

Таким образом, именно уменьшение диаметра пролетного канала (внутреннего диаметра ЗС типа спираль) на некотором участке ЛБВ перед выводом энергии в сочетании с меньшим шагом ЗС обеспечивает наиболее сильное повышение устойчивости к самовозбуждению на обратной волне при одновременном повышении электронного КПД.

Источники информации

1. Fleury G., Devillé С, and Kuntzmann J.-С. Average power limits of brazed-helix TWT's // Intern. Electron Devices Meet. Washington, D.C. - New York, 1980. P.806-809.

2. Ильина E.M., Мятежников С.А., Поляков И.В. Мощная широкополосная лампа бегущей волны со скачками диаметра пролетного канала. // Радиотехника и электроника. 2007. Т.52, №8. С.1018-1023.

3. Кудряшов В.П. Побочные колебания в широкополосных ЛБВО (по данным отеч. и зарубежн. печати за 1952-1972 гг.): Обзоры по электронной технике. - М.: ЦНИИ «Электроника», 1977. Сер.1, Электроника СВЧ. Вып.3 (442). 85 с.

4. Силин Р.А., Сазонов В.П. Замедляющие системы. - М.: Сов. радио, 1966. 632 с.

Широкополосная лампа бегущей волны (ЛБВ), содержащая замедляющую систему (ЗС) типа спираль, отличающаяся тем, что имеет на выходе участок, диаметр пролетного канала d (внутренний диаметр ЗС) которого плавно или скачкообразно уменьшается по направлению к выводу энергии, при этом минимальный диаметр пролетного канала d₂ на участке удовлетворяет условию d₂≤0,95d₁, а шаг спирали на отрезке этого участка h₂ удовлетворяет условию h₂≤(d₂/d₁)·h₁, где d₁ и h₁ - диаметр пролетного канала и шаг спирали до участка с уменьшающимся диаметром соответственно.