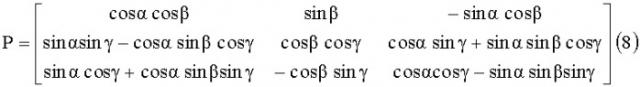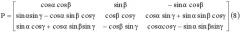Способ определения параметров характеристики преобразования трехкомпонентного магнитометра

Способ определения параметров характеристики преобразования трехкомпонентного магнитометра

Иллюстрации

Показать все

Реферат

Изобретение относится к области магнитных измерений, в частности к измерениям компонент и полного вектора индукции магнитного поля Земли (МПЗ), а также к средствам калибровки трехкомпонентных магнитометров.

Как известно, основными причинами неидеальности статической характеристики преобразования трехкомпонентных магнитометров являются присутствие мультипликативных погрешностей, вызванных как отклонениями коэффициентов преобразования от номинальных значений, так и отклонениями магниточувствительных осей (МЧО) магнитометра от его геометрических осей (ортогонального базиса), а также присутствие аддитивных погрешностей, вызванных смещением нуля преобразователей магнитометра. Следовательно, необходимая точность и простота реализации способа измерения и учета указанных погрешностей определяют его эффективность и целесообразность выбора.

Известны способы повышения точности калибровки магнитометров [1-4], основанные на применении метода образцовых мер, которые включают размещение датчика трехкомпонентного магнитометра в центре образцовой трехкомпонентной меры магнитной индукции, ориентацию чувствительных осей магнитометра вдоль осей меры, поочередное воспроизведение известного значения магнитной индукции вдоль каждой оси меры, регистрацию выходных сигналов магнитометра по всем его компонентам, построение нормированной приборной квадратной матрицы и использование ее для нахождения корректирующей матрицы.

Указанные способы сложны в реализации и обладают высокой стоимостью. Необходимость обязательного использования дорогостоящей уникальной конструкции экранированной меры магнитной индукции или колец Гельмгольца, предполагающих наличие сложно настраиваемых катушек или колечной системы, усложняет возможность их приобретения и содержания.

Неравномерность пространственного распределения формируемого магнитного поля внутри катушек магнитной меры вызывает потребность локализации ограниченных размеров рабочего объема, что создает трудности при установке и размещении в этом объеме калибруемых датчиков. Кроме того, сложность точного определения или формирования геометрической направленности магнитных осей образцового магнитного поля и сложность юстировки осей меры по обеспечению их ортогональности создают практическую невозможность ориентации геометрических осей, а тем более тройки неортогональных магниточувствительных осей магнитометра вдоль соответствующих осей меры в процессе калибровки.

Таким образом, указанные недостатки и сложность содержания и обслуживания меры магнитной индукции или колечной системы ограничивают возможности применения известных способов определения параметров характеристики преобразования трехкомпонентного магнитометра.

В [5] показан способ определения параметров градуировочной характеристики одноосного (однокомпонентного) магнитометра, включающий совмещение его МЧО с осью направления вектора индукции МПЗ известного значения его модуля, определение результата преобразования этого значения магнитометром, а затем определение результатов преобразования последовательности дополнительных воздействующих на вход магнитометра образцовых значений магнитной индукции, формируемых последовательностью фиксированных поворотов МЧО магнитометра относительно оси направления вектора индукции МПЗ на известные углы в диапазоне их значений от нуля до 180°, причем общее количество входных воздействий и соответственно преобразование их магнитометром равно степени аппроксимирующего градуировочную характеристику полинома, затем определение параметров градуировочной характеристики в виде результатов решения системы уравнений, заданной в виде системы функций входных воздействий и параметров градуировочной характеристики магнитометра.

Полезность и преимущественные особенности данного способа обусловлены возможностью использования для его осуществления сравнительно простых в изготовлении и низкой стоимости малогабаритных прецизионных поворотных устройств в сочетании с использованием в качестве образцового источника равномерно распределенной в пространственном объеме индукции МПЗ.

Недостатком данного способа является ограничение возможности применения его для определения всех необходимых параметров характеристики преобразования трехкомпонентного магнитометра.

Известен способ определения углов отклонения магниточувствительных осей феррозондов трехкомпонентного магнитометра от его собственных геометрических осей ортогонального базиса [6], который наиболее близок по технической сущности к предлагаемому и принят за прототип.

В известном способе искомые шесть углов, а следовательно, и направляющих косинусов, определяют непосредственно в геомагнитном поле на главных магнитных курсах 0, 90°, 180° и 270° путем последовательных поворотов блока феррозондов, например, вокруг вертикальной оси, для этого магниточувствительный блок магнитометра устанавливают на специальном поворотном столе так, что продольная ось одного из преобразователей оказывается совмещенной с вертикалью, а продольные оси двух других преобразователей - лежащими в горизонтальной плоскости, после разворота блока вокруг вертикальной оси с наблюдением показаний на главных курсах искомые углы вычисляют в виде функций результатов преобразований и угла магнитного наклонения.

Недостатками данного способа являются низкая точность, обусловленная неполным количеством определяемых параметров характеристики преобразования магнитометра, таких как истинное значение коэффициентов преобразования, смещение нуля преобразователей и учет погрешностей, обусловленных несоосностью магниточувствительных и геометрических осей магнитометра. То есть для определения полного количества всех параметров характеристики преобразования в данном случае кроме средств, необходимых для реализации данного способа, необходимо применение экранированной меры магнитной индукции или колец Гельмгольца.

Целью предлагаемого изобретения является повышение точности измерения определением полного набора параметров характеристики преобразования трехкомпонентного магнитометра.

Предлагаемый способ определения параметров характеристики преобразования трехкомпонентного магнитометра включает предварительное измерение проекций вектора индукции магнитного поля Земли на оси опорной системы координат и четыре преобразования магнитометром проекций этого вектора на его магниточувствительные оси при фиксированных поворотах, например, на углы, кратные 90°, геометрических осей, по крайней мере в двух взаимно перпендикулярных плоскостях их расположения и по измеренным проекциям вектора индукции МПЗ и результатам преобразований, заданным в виде функций углов поворота и в совокупности представляющих собой системы независимых линейных уравнений, определяются искомые параметры характеристики преобразования в виде решения указанных систем уравнений, единственность решения которых является условием предварительного выбора углов поворота.

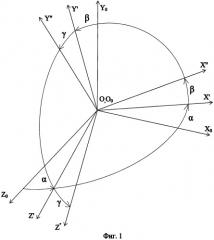
На фигуре 1 показан общий случай ориентации геометрических осей ортогональной системы координат магнитометра относительно опорной системы координат.

Математическое выражение характеристики преобразования [2, 6] трехкомпонентного магнитометра в его собственной системе координат OXYZ можно представить в виде следующей зависимости измеренных значений вектора индукции магнитного поля Земли от истинных значений составляющих B_m(m=x,y,z) этого вектора

где a _mj(m, j=X,Y,Z) и a _mc - реальные параметры характеристики преобразования магнитометра, определяющие ее неидеальность, причем:

a _XX, a _YY, a _ZZ - реальные значения коэффициентов преобразования соответственно компонент B_X, B_Y, B_Z, неидеальность которых определяется отличием их от номинальных значений, причем отличие обусловленно погрешностью масштабов преобразования и несоосностью магниточувствительных осей датчика с соответствующими им геометрическими осями OX, OY, OZ ортогонального базиса магнитометра;

a _mj(m≠j) - параметры, характеризующие неортогональность поперечных (j-X) магниточувствительных осей относительно продольных (m-Х) осей магнитометра;

a _mc - параметры, характеризующие смещение нуля характеристик преобразования m-Х измерительных каналов магнитометра;

N_m - результат измерения, формируемый, например, в виде кодового эквивалента.

В данном случае выражение идеальной характеристики преобразования имеет следующий вид:

N_X=a _XXHB_X,

N_Y=a _YYHB_Y,

N_Z=a _ZZHB_Z,

где a _XXH, a _YYH, a _ZZH - номинальные (идеальные) значения коэффициентов преобразования.

Выражение (1) можно представить в матричном виде

где А, Ас - матрицы определяемых параметров a_mj и a_mc, то есть

R - матрица результатов измерений компонент вектора индукции МПЗ

М - матрица компонент вектора индукции МПЗ в собственной ортогональной системе координат OXYZ магнитометра

По результатам найденных значений параметров a_mj, a_mc измеряемые магнитометром величины B_X, B_Y, B_Z можно определить решением с помощью вычислительного устройства системы уравнений (2) в матричном виде

Компоненты вектора индукции МПЗ (5) можно представить в виде

где B_X0, B_Y0, B_Z0 - элементы матрицы М₀ или компоненты вектора индукции МПЗ в координатах опорной системы координат O₀X₀Y₀Z₀, с заданной ее постоянной ориентацией относительно вектора индукции МПЗ;

Р - матрица преобразования (поворота) проекций B_X0, B_Y0, B_Z0 в проекции B_X, B_Y, B_Z, связанной с геометрическими осями магнитометра системы координат OXYZ.

Взаимное положение систем O₀X₀Y₀Z₀ и OXYZ характеризуется тремя углами поворота α, β и γ относительно базовой плоскости, то есть в данном случае плоскости расположения осей О₀Х₀, O₀Z₀. Согласно [7]

где α - угол между проекцией оси ОХ на базовую плоскость и осью О₀Х₀;

β - угол между осью ОХ и проекцией ОХ на базовую плоскость;

γ - угол между осью OZ и линией пересечения базовой плоскости с плоскостью, содержащей оси OY, OZ.

Положительные направления углов ориентации α, β и γ в соответствующих плоскостях при повороте геометрических осей системы координат OXYZ магнитометра относительно выбранной опорной системы координат O₀X₀Y₀Z₀ показаны на фигуре 1. В данном случае на фигуре 1 обозначениям OX', OX'', OY', OY'', OZ', OZ'' соответствуют промежуточные и конечные положения осей OX, OY, OZ.

Выражение (2), представленное в виде совокупности последовательных преобразований

является выражением линейной системы уравнений в общем виде. Систему (9) можно представить с учетом выражений (1), (3)-(5) в виде следующих трех подсистем уравнений

Параметры a _mj, a _mc характеристики преобразования магнитометра определяются решением полученных систем уравнений после подстановки в них результатов измерений N_Xi, N_Yi, N_Zi и значений (5) компонент B_Xi, B_Yi, B_Zi вектора индукции МПЗ, полученных в результате матричных преобразований

Все полученные системы уравнений (10)-(12) имеют общий определитель, представленный в следующем виде

Следует отметить, что не все возможные комбинации поворотов, определяющих матрицы P_i, гарантируют формирование систем линейных независимых уравнений с единственным решением. Условием существования единственного решения полученных систем уравнений является выбор матричных преобразований P_i для формирования матриц M_i, обеспечивающих неравенство нулю определителя (Δ≠0).

Одними из важных критериев выбора ориентации опорной системы координат в данном случае являются, например, наличие или выбор необходимых средств измерения или задания углов пространственной ориентации ее осей и используемая в качестве образцового сигнала абсолютная величина проекций вектора индукции МПЗ на базовую плоскость, определяющую ориентацию этой системы. Рассмотрим, например, первый вариант ориентации опорной системы координат O₀X₀Y₀Z₀, у которой базовая плоскость ориентирована в горизонте, причем ось О₀Х₀ совпадает с направлением горизонтальной составляющей B_X0 вектора индукции МПЗ, касательного к магнитному меридиану и направленного на северный магнитный полюс, ось O₀Y₀ совпадает с вертикальной составляющей B_Y0 вектора индукции МПЗ, а ось OZ перпендикулярна осям О₀Х₀ и O₀Y₀ и направлена в сторону востока, В данном случае

В выражении (7) элементы матрицы М₀ являются известными значениями измеренных компонент B_X0, B_Y0, B_Z0 в опорной системе координат. Элементы матрицы Р, формируемые поворотным устройством, определяют положение объекта относительно опорной системы координат. Элементы матрицы R также являются известными значениями, то есть результатами измерений калибруемым магнитометром. Задачей изобретения является реализация оптимальных матричных преобразований для получения системы уравнений, решением которой являются неизвестные значения элементов матриц А и А_С, определяемых выражениями (3).

Осуществим четыре измерения проекций вектора индукции МПЗ при заданных углах поворота геометрических осей магнитометра в двух взаимно перпендикулярных плоскостях. Например, первое измерение компонент осуществим в начальном положении, то есть при α₁=β₁=γ₁=0; второе - при α₂=90°, β₂=0, γ₂=90°; третье - при α₃=180°, β₃=γ₃=0 и четвертое измерение - при α₄=180°, β₄=0, γ₄=180°. Выражения матрицы Р при этом при подстановке выбранных значений углов в (8) приводятся к виду

Подставляя выражение (15) и полученные выражения (16) в выражение (13), получим

Подстановкой полученных компонент B_Xi, B_Yi, B_Zi в выражение (14) имеем

Δ=-4B_X0B_Y0 ²,

то есть Δ≠0. Следовательно, после подстановки полученных компонент в выражения (10)-(12) имеем следующие системы независимых линейных уравнений

Решением первой системы уравнений являются выражения параметров

, , ,

Результат решения второй системы уравнений

, , ,

и наконец, решением третьей системы уравнений являются

, , ,

В данном примере согласно формуле изобретения осуществляются четыре преобразования (i=1,2,3,4) проекций B_Xi, B_Yi, B_Zi на магниточувствительные оси при поворотах геометрических осей в двух взаимно перпендикулярных плоскостях их расположения, то есть осей OX, OZ в плоскости YOZ при углах поворота α₁, β₁, γ₁ и α₃, β₃, γ₃ и осей OY, OZ в плоскости YOZ при α₂, β₂, γ₂ И α₄, β₄, γ₄.

Рассмотрим теперь пример второго варианта положения опорной системы координат O₀X₀Y₀Z₀ относительно вектора индукции у которой одна из осей, например О₀Х₀, совпадает с направлением вектора индукции а направления осей O₀Y₀, O₀Z₀ так же, как и в первом варианте, перпендикулярны направлению этого вектора и образуют правую систему координат. В данном случае

Аналогично первому варианту осуществим четыре измерения проекций вектора на оси системы координат OXYZ. Можно убедиться, что при тех же углах поворота этих осей, то есть при матричных выражениях (16) получим нулевое значение определителя (Δ=0). Для исключения этого равенства изменим некоторые значения углов поворота. Так, например, при значениях углов

α₁=0, α₂=90°, α₃=180°, α₄=α₂=90°, β₁=β₂=β₃=β₄=γ₁=γ₂=γ₃=0, γ₄=90° имеем

, , , .

Подставляя эти выражения в (13) с учетом (17), получим

Далее подстановкой полученных значений компонент в выражение (14) получим Δ=Т³, то есть Δ≠0. Следовательно, подстановкой компонент в выражения (10)-(12) получаются следующие системы независимых линейных уравнений

Решением первой системы уравнений являются выражения

, , ,

Решением второй системы уравнений получим выражения

, , ,

Результатом решения третьей системы уравнений являются

, , ,

В данном случае осуществляются, так же как и в первом варианте, четыре преобразования проекций вектора индукции МПЗ при поворотах геометрических осей в тех же двух взаимно перпендикулярных плоскостях. Возможны также варианты выбора поворотов и в трех взаимно перпендикулярных плоскостях при выполнении условия Δ≠0.

Таким образом, на примере двух вариантов показана возможность определения параметров характеристики преобразования с помощью несложных преобразований и вычислений, а следовательно, возможность повышения точности измерения компонент вектора индукции МПЗ, определяемых в данном случае с помощью выражения (6).

Преимущественной особенностью второго варианта выбора опорной системы координат является возможность использования полного значения модуля вектора индукции МПЗ в качестве образцового сигнала для определения параметров характеристики преобразования. Возможность определения параметров не ограничивается использованием только рассмотренных вариантов выбора опорной системы координат и ориентации геометрических осей магнитометра, но и в других случаях выбор определяется наличием необходимых поворотных или углоизмерительных средств. Во всех случаях предложенный способ предусматривает минимизацию количества необходимых поворотов для формирования систем независимых линейных уравнений.

Точность определения параметров характеристики преобразования зависит от точности измерения значений модуля и направления вектора индукции МПЗ и точности задания углов поворота. Измерение модуля Т легко осуществимо, например, протонным или квантовым магнитометром. Для точного определения направления вектора индукции МПЗ применимы различные известные технические средства, например показанные в работах [6, 8].

Известным способом реализации прецизионных поворотных устройств является, например, применение трехстепенных карданных устройств. Практически удобным вариантом является устройство [9], представляющее собой куб с ортогонально выполненными поверхностями, внутри которого заключен магниточувствительный трехосный датчик, геометрические оси которого строго коллинеарны соответствующим ребрам куба. Данное устройство позволяет установкой граней куба на базовой плоскости и точной установкой его ребер вдоль осей опорной системы координат обеспечивать заданную и точную ориентацию геометрических осей магнитометра относительно осей опорной системы координат.

Простота и эффективность применения данного способа, основанного на решении простых систем линейных уравнений, в сочетании с возможностью применения простых и доступных калибровочных и вычислительных средств определяют его новизну, полезность, преимущественные особенности и реализуемость. Следовательно, предлагаемое изобретение может найти широкое применение в технике магнитных измерений.

Литература

1. Патент США №6130534, кл. G01R 35/00, G01R 33/02, 10.10.2000.

2. Афанасьев Ю.В. Феррозондовые приборы. - Л.: Энергоатомиздат. Ленингр. отд-ние, 1986. С.172-179.

3. Способ определения корректирующей матрицы трехкомпонентного магнитометра. Патент РФ №2229727, МПК 7 G01R 35/00, 33/02, 27.11.2002.

4. Способ определения калибровочной матрицы трехкомпонентного магнитометра (варианты). Патент РФ №2262711, МПК G01R 33/02, 14.11.2003.

5. Способ определения параметров градуировочной характеристики магнитометра. Патент РФ №2386141, МПК G01R 35/00, 7 G01R 33/02, 04.07.2008.

6. Афанасьев Ю.В., Студенцов Н.В., Щелкин А.П. Магнитометрические преобразователи, приборы, установки. - Л.: Энергия, 1972. С.247-250.

7. С.С.Ривкин. Статистический синтез гироскопических устройств. Л.: Судостроение, 1970. С.74.

8. Способ измерения полного вектора магнитного поля, а также устройство для его осуществления. Патент РФ №2218577, МПК 7 G01R 33/02, 09.11.2001.

9. Трехкомпонентный датчик магнитного поля. АС 312216, МПК G01r 33/02, 06.04.1970.

Способ определения параметров характеристики преобразования трехкомпонентного магнитометра вращением в опорной системе координат его геометрических осей, предварительно совмещенных с соответствующими осями опорной системы координат и жестко связанных с его магниточувствительными осями, включает предварительное измерение проекций вектора индукции магнитного поля Земли на оси опорной системы координат и преобразование магнитометром проекций этого вектора на его магниточувствительные оси соответственно при разных положениях его двух геометрических осей, лежащих в одной из плоскостей опорной системы координат при фиксированных поворотах их, например, на углы, кратные 90°, вокруг третьей геометрической оси, отличающийся тем, что осуществляются всего четыре преобразования магнитометром проекций вектора индукции магнитного поля Земли на магниточувствительные оси при фиксированных поворотах, например, на углы, кратные 90°, геометрических осей, по крайней мере в двух взаимно перпендикулярных плоскостях их расположения и по измеренным проекциям вектора индукции магнитного поля Земли и результатам преобразований, заданным в виде функций углов поворота и в совокупности представляющих собой системы независимых линейных уравнений, определяются искомые параметры характеристики преобразования в виде решения указанных систем уравнений, единственность решения которых является условием предварительного выбора углов поворота.