Способ картографического отображения двухмерных распределений, заданных в цифровой форме

Способ картографического отображения двухмерных распределений, заданных в цифровой форме

Иллюстрации

Показать все

Реферат

Изобретение относится к области геодезии и картографии, в частности к картографическому моделированию при структурно-тектонических, геофизических, геохимических и т.п. исследованиях, при поисково-разведочных работах, инженерно-геологических изысканиях и т.д.

Известен оптический способ построения карт плотности распределения заданных графическим способом элементов (пятен, точек и линий) на исследуемой площади, включающий преобразование изображений дискретных графических распределений в непрерывную полутоновую форму с дальнейшим их представлением в форме изолиний эксинденсит (авторское свидетельство SU №365562, 1970 [1]). Однако данный способ не предусматривает обработку данных, заданных в цифровой форме.

Известен также способ картографического отображения двумерных распределений, заданных в цифровой форме, включающий преобразование изображений дискретных графических распределений в непрерывную полутоновую форму с дальнейшим их представлением в форме изолиний - эксинденсит, в котором с целью повышения точности при оптическом моделировании кодируют цифровые значения признака в заданной точке планшета оптическими символами - разновеликими пятнами с оптической плотностью, пропорциональной величине признака (авторское свидетельство SU №640113, 1978 [2]), что обеспечивает отображение двумерных распределений, заданных в цифровой форме.

Однако в большинстве случаев картографического отображения необходимо построение трехмерной модели рельефа, заданной в аналитическом виде при отображении результатов экологического состояния регионов (патент RU №2079891, заявка №92007530 от 23.11.1992 [3]), результатов ситуационного мониторинга объектов хозяйственной деятельности, например морских газонефтяных месторождений и терминалов, включая подводные исследования с отображением рельефа местности, что известными способами не обеспечивается.

Известен также способ построения трехмерной модели рельефа в виде кусочных сплайн-функций двух переменных. Исходной информацией служит типографская карта местности. Способ реализуется посредством геопространственной информационной системы (ГИС) (Берлянт A.M. Картография. - М.: Аспект Пресс, 2002. - 336 с. [4]). Эффективность аналитической обработки данных в геопространственных информационных системах в значительной степени зависит от возможностей, обеспечиваемых цифровой моделью рельефа (ЦМР), определяемой как совокупности высотных отметок, взятых в узлах некоторой регулярной или нерегулярной сети точек с заданными координатами [4]. В автоматизированных системах ЦМР служит основой получения прямой и косвенной информации о рельефе местности. Например, получение информации о морфометрических данных, включая вычисление углов наклона и экспозиции склонов; анализ видимости/невидимости; построение трехмерных изображений; профилей поперечного сечения; оценку формы склонов через кривизну их поперечного и продольного сечения; вычисление положительных и отрицательных объемов; генерацию линий сети тальвегов и водоразделов, образующих каркасную сеть рельефа, его структурных линий и иных особых точек рельефа: локальных минимумов (впадин) и локальных максимумов (вершин), седловин, бровок, линий обрывов и иных нарушений «гладкости» поверхности и т.д.

Источниками исходных данных для создания ЦМР, например, суши служат топографические карты, аэрофотоснимки, космические снимки, данные альтиметрических измерений, морские навигационные карты, данные промерных гидрографических работ. При этом принята следующая технология построения ЦМР (Суворов С.Г., Дворецкий Е.М., Коваленко С.А. Методика создания цифровых моделей рельефа повышенной точности // Информация и космос. №1, 2005 - с.52-54 [5]). Вся доступная информация оцифровывается. Полученные от разнообразных источников данные сводятся в единый набор координат точек и высот в них. Этот набор триангулируется (обычно методом Делоне). Процедура триангуляции дает систему непересекающихся треугольников, покрывающих рассматриваемую область поверхности земли (TIN-модель). В результате чего рельеф представляется многогранной (элементарная грань - треугольник) поверхностью с высотными отметками (отметками глубин) в узлах треугольной сети. Каждая грань этой поверхности описывается либо линейной функцией (полиэдральная модель), либо полиномиальной поверхностью, коэффициенты которой определяются по значениям в вершинах граней-треугольников. Эта технология в различных вариантах реализована во всех применяемых на практике ГИС.

При этом цель построения ЦМР - получение адекватной прямой и косвенной информации о рельефе в автоматизированных системах - не достигается. Источником всех недостатков этой технологии является этап триангуляции. При этом рельеф представляется в виде непрерывной функции, но с разрывами уже в соответствующей функции первого дифференциала на ребрах триангуляции (т.е. негладкая функция). Это противоречит модели рельефа, которая принята при построении топографических или навигационных карт, где поверхность рельефа представляется гладкой функцией. Кроме того, истинное назначение триангуляции - это задать порядок (сеть) по степени близости и взаимному расположению на множестве точек в плоскости, следовательно, при этом не учитывается взаимоотношение высот (глубин) между точками, что приводит к искажению пространственного направления и смещению в местоположении структурных линий рельефа. К основным видам структурных линий рельефа относятся гребневые и килевые линии, линии выпуклого и вогнутого перегибов. Под гребневыми линиями, или водоразделами, понимают линии плановой корреляции точек с максимальными высотами. Килевые линии (тальвеги, русла) соединяют точки с минимальными высотами. Кроме того, результат триангуляции резко и непредсказуемо изменится при изменении исходного набора точек, т.е. при удалении, добавлении точки (точек) или при изменении координат в исходном массиве точек. Это свойство триангуляции не позволяет «управлять» (редактировать) построением локальной формы рельефа. Кроме того, если ЦМР при этом построена с использованием триангуляции, то результаты вычислений дифференциалов рельефа различных порядков не являются достоверными. Можно констатировать, что в этой области геоинформатики существует проблемная ситуация, выражающаяся в том, что технология построения ЦМР с использованием процедуры триангуляции не позволяет достичь требуемой цели. Разрешение сложившейся проблемной ситуации можно путем применения таких средств построения ЦМР, которые не используют процедуру триангуляции и которые приводят к построению всюду гладкой поверхности, что и реализовано в известном техническом решении (патент RU №2415381 С1, 27.08.2011 [6]).

В известном способе картографического отображения двухмерных распределений, заданных в цифровой форме, включающим преобразование изображений дискретных графических распределений в непрерывную полутоновую форму с дальнейшим их представлением в форме изолиний - эксинденсит, в котором при оптическом моделировании кодируют цифровые значения признака в заданной точке планшета оптическими символами - разновеликими пятнами с оптической плотностью, пропорциональной величине признака, построение рельефа местности, в отличие от аналогов [1-5], построение рельефа местности выполняют путем интерполяции точек высот (глубин) в виде двумерных нерегулярных рациональных фундаментальных сплайнов, путем построения двумерной сплайн-функции, определяемой как тензорное произведение одномерных сплайнов [6].

Известный способ [6] включает интерполяцию точек высот (глубин) методами двумерных сплайн-функций, а конкретно в виде двумерных нерегулярных рациональных фундаментальных сплайнов (NURBS) (Голованов Н.Н. Геометрическое моделирование. - М.: Физматлит, 2002. - 472 с.[7]). Преимуществом данного способа является выполнение интерполяции точек высот в виде двумерных рациональных двумерных сплайн-функций NURBS, что позволяют построить гладкую поверхность для любой формы рельефа, даже для обрывов с отрицательным углом наклона. Во-вторых, поверхность рельефа задается аналитической зависимостью, т.е. конечным набором параметров фиксированного набора функций (полиномиальных сплайнов). Аналитическая форма задания рельефа, т.е. в виде суперпозиции аналитических функций от двух переменных, позволяет использовать весь аппарат дифференциальной геометрии для описания морфометрических свойств рельефа, например вычисления значения функции (высоту, глубину) или ее дифференциала (уклон) в любой точке (точках) области задания функции. В-третьих, NURBS обеспечивают возможность локального редактирования формы поверхности. Кроме того, для одной и той же области земли объем массива данных ЦМР при использовании NUBRS будет как минимум на порядок меньше, чем при традиционном точечном представлении. Применение NURBS повышает эффективность автоматизированных геопространственных систем за счет уменьшения времени обработки и требуемого объема памяти. Применение NURBS в вычислительной технике уже давно свершившийся факт - в графических пакетах всех операционных систем встроены алгоритмы обработки и визуализации NURBS, например в графических пакетах низкого уровня: DirectX и OpenGL для Windows. Однако при построении ЦМР возникают препятствия, связанные с эффектом возникновения в некоторых ситуациях нарушения монотонности в изменении поверхности - локальное появление ложных осцилляций. В известном способе это препятствие устраняется либо путем добавления новых точек в массив для интерполяции, либо путем использования методов изогеометрической аппроксимации сплайнами (Квасов Б.И. Методы изогеометрической аппроксимации сплайнами. - М. - Ижевск: НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2006. - 416 с. [8]). В первом случае разрешение проблемы связано с повышением значимости работы эксперта в итерационной процедуре построения NURBS, во втором с существенным усложнением математических алгоритмов технологии.

В известном способе реализована технология построения ЦМР на основе NURBS в виде итерационной экспертной автоматизированной процедуры. В качестве языка программирования использован язык MatLab. В этой системе качество построения ЦМР определяется путем экспертного сравнения положения изолиний, вычисленных по NURBS, с положением соответствующих изогипс (изобат) на исходной карте.

В конкретной реализации известного способа источником информации о рельефе служат растровые карты.

В общем случае при аппроксимации профиля рельефа одномерными сплайнами задают значения двух первых производных в конечных точках разреза. Однако такая информация неизвестна, и получить ее на практике нельзя. Поэтому в качестве базового сплайна для аппроксимации профиля рельефа по разрезу использован простейший кубический сплайн с нулевыми граничными производными. Согласование первых двух дифференциалов ЦРМ для смежных прямоугольных участков карты обеспечивается перекрытием областей задания смежных NURBS.

Технология построения ЦМР в аналитическом виде на основе NURBS позволяет исключить этап триангуляции и тем самым исключить недостатки существующих технологий.

Однако при составлении ЦМР в обеспечение проведения геологических и сейсмических подводных исследований необходимо выполнять более подробную детализацию рельефа морского дна для выбора мест установки донной измерительной аппаратуры.

Отсутствие дифференцируемости у фрактальных функций приводит к необходимости использовать специфический аппарат для их представления. К такому аппарату можно отнести два вида инструментальной техники: системы итерирующих функций (Iterated Function Systems - IFS) и вейвлеты. Эти инструменты позволяют представить фрактальную функцию в виде предфрактала только как среднее (средне взвешенное значение) на дискретном множестве ячеек (точек), обычно регулярном. Площадь ячеек соответствует некоторому масштабу, кратному степени двойки. Для IFS вообще отсутствуют какие-либо принципиальные ограничения на значения масштаба. Для вейвлетов возможны все масштабы, меньшие некоторого максимального, определяемого только плотностью исходных данных.

Методы представления рельефа с помощью IFS и вейвлетов позволяют осуществить (Sahr K., White D., Kimerling A. Geodesic Discrete Global Grid Systems // Cartography and Geographic Information Science, Vol. 30, No. 2, 2003, pp.121-134. White. D. Global Grids From Recursive Diamond Subdivisions of The Surface of an Octahedron or Icosahedron. // Environmental Monitoring and Assessment, 4(1), 2000, pp.93-103. Bartholdi. J., Goldsman P. Continuous Indexing of Hierarchical Subdivisions of the Globe. // Int. J. Geographical Information Science, 15(6), 2001, pp.489-522. Goodchild M.F., Yang S. A Hierarchical Data Structure for Global Geographic Information Systems. // Computer Vision and Geographic Image Processing, 54(1), 1992, pp.31-44. Matos P. SMOS L1 Processor Discrete Global Grids Document - DEIMOS, Engenharia, 2003. - 64 pp. Lessig C. Orthogonal and Symmetric Haar Wavelets on the Sphere - University of Toronto, 2007. - 169 pp. Peter Schroder and Wim Sweldens. Spherical wavelets: Efficiently representing functions on the sphere. Computer Graphics Proceedings (SIGGRAPH 95), 1995, pages 161-172):

- двоичную генерализацию поверхности, заданную на регулярной сетке точек;

- имитацию увеличения масштаба разрешения исходной информации;

- выявление резких перепадов значений функции;

- вычисление фрактальных параметров функции;

- фильтрацию "шума".

При этом могут быть реализованы следующие операции:

- восстановления рельефа по дискретным измерениям;

- решения обратной задачи IFS;

- нахождения оптимальных непрерывных и дискретных семейств вейвлетов для представления рельефа.

Данные операции могут быть реализованы на методах описания рельефа с помощью функций Морса, графов Кронрода-Риба и комплексов Морса-Смейла, что обеспечит возможность:

- топологического кодирования форм рельефа;

- картографической генерализации;

- распознавания геоморфологических объектов;

- формальной классификации геоморфологических объектов;

- замощения поверхности рельефа семейством параметризованных (полиномиальных) функций, заданных на клетках Морса-Смейла;

- иерархически оценивать степень сходства двух карт рельефа, представляющих одну область, в одном или разных масштабах;

- оценки достоверности выделенных форм рельефа с учетом погрешности и мощности исходной информации;

- оценки степени достаточности набора точечных измерений для восстановления рельефа с заданной подробностью.

Задачей предлагаемого технического решения является расширение функциональных возможностей с одновременным повышением достоверности способа картографического отображения двумерных распределений, заданных в цифровой форме на основе алгоритмов восстановления рельефа по дискретным измерениям с использованием топологических карт; формирования графа Кронрода-Риба для кусочно-линейной поверхности; формирования комплексов Морса-Смейла для кусочно-линейной поверхности; упрощения кусочно-линейной поверхности с использованием полученной для нее структур графа Кронрода-Риба и комплексов Морса-Смейла; оценки фрактальных параметров рельефа на основе заданных структур графа Кронрода-Риба и комплексов Морса-Смейла.

Поставленная задача решается за счет того, что в способе картографического отображения двухмерных распределений, заданных в цифровой форме, включающем преобразование изображений дискретных графических распределений в непрерывную полутоновую форму с дальнейшим их представлением в форме изолиний - эксинденсит, в котором при оптическом моделировании кодируют цифровые значения признака в заданной точке планшета оптическими символами - разновеликими пятнами с оптической плотностью, пропорциональной величине признака, построение рельефа местности выполняют путем интерполяции точек высот и/или глубин в виде двумерных нерегулярных рациональных фундаментальных сплайнов, путем построения двумерной сплайн-функции, определяемой как тензорное произведение одномерных сплайнов, в котором, в отличие от прототипа, при построении рельефа местности определяют итерирующие функции и вейвлеты для представления фрактального рельефа, путем формирования для кусочно-линейной поверхности графа Кронрода-Риба и комплексов Морса-Смейла, при этом выполняют упрощения кусочно-линейной поверхности с использованием полученной для нее структур графа Кронрода-Риба и комплексов Морса-Смейла; оценку фрактальных параметров рельефа на основе заданных структур графа Кронрода-Риба и комплексов Морса-Смейла.

Сущность реализации предлагаемого способа поясняется чертежами.

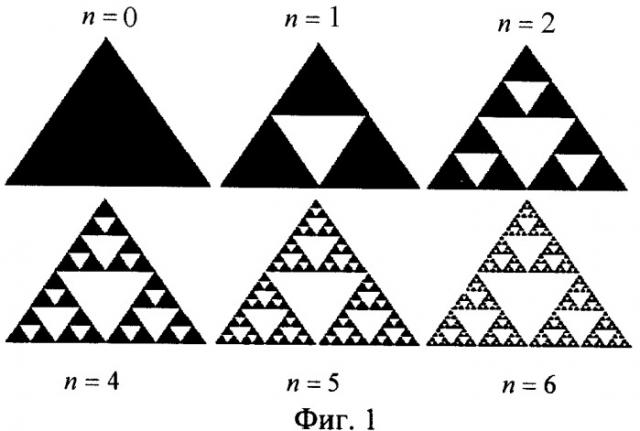
Фиг.1. Иллюстрация последовательности первых шести предфракталов, в процедуре построения фрактальной линии («ковер Серпинского») с индексом ветвления, равным или большим трем для внутренних точек (удаляемые треугольники обозначены белым цветом).

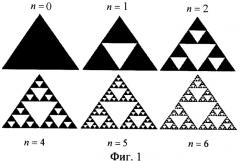
Фиг.2. Графический результат рекурсивного применения матричных выражений.

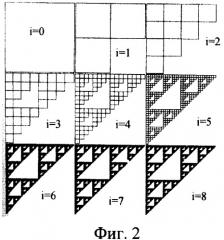
Фиг.3. Иллюстрация определения расстояния между точкой х и подмножеством В, а также расстояния от подмножества В, и от В до А.

Фиг.4. Графическая иллюстрация действия IFS. Позициями обозначены: исходное изображение 1, три последующие итерации 2, 3, 4 соответственно.

Фиг.5. Начальные шаги генерации фрактальной поверхности с помощью IFS. Последовательности генерации 5, 6, 7, 8.

Фиг.6. Аппроксимация IFS предфрактала 9 другим предфракталом 10.

Фиг.7. Частотно-временная диаграмма для преобразования Фурье (фиг.7а) и масштабно-временная диаграмма для вейвлет-преобразования (фиг.7б). Частота 11, амплитуда 12, масштаб 13.

Фиг.8. Схема двумерной вейвлет-декомпозиции. Фиг.8а - Цепочка вычислений, фиг.8б - масштабное соответствие уровней декомпозиции. Исходные данные 14, первый уровень 15 декомпозиции, второй уровень 16 декомпозиции, третий уровень 17 декомпозиции.

Фиг.9. Примеры имитации рельефа фракталами.

Фиг.10. Поведение функции f(x, y) вблизи критической точки с координатами (0,0). Минимум - а, седло - с, максимум - d.

Фиг.11. График поверхности вблизи точки с координатами (0,0) для вырожденной критической точки типа «обезьяньего седла».

Фиг.12. Граф Кронрода-Риба. Фиг.12а, б - контурное изображение функции, для которой построен граф Кронрода-Риба, фиг.12в - граф Кронрода-Риба, фиг.12г - вложение графа Конрода-Риба в плоскость контурного рисунка функции: максимумы - точки I, J, G, минимумы - точки D, А, В, L, седла - точки Н, F, Е, С, K.

Фиг.13. Иллюстрация перехода от гладкой поверхности к симплициальному комплексу. Гладкая поверхность 18, симплициальный комплекс 19.

Фиг.14. Симплексы малой размерности.

Новые отличительные признаки заявляемого способа, заключающиеся в том, что при построении рельефа местности определяют итерирующие функции и вейвлеты для представления фрактального рельефа, путем формирования для кусочно-линейной поверхности графа Кронрода-Риба и комплексов Морса-Смейла, при этом выполняют упрощения кусочно-линейной поверхности с использованием полученной для нее структур графа Кронрода-Риба и комплексов Морса-Смейла; оценку фрактальных параметров рельефа на основе заданных структур графа Кронрода-Риба и комплексов Морса-Смейла, основаны на следующих постулатах.

Первый постулат (непрерывности) - рельеф Земли представляет собой непрерывную поверхность.

Второй постулат (топологический) - рельеф Земли представляет собой замкнутую двумерную поверхность в трехмерном пространстве, топологически эквивалентную двумерной сфере.

Эти два очевидных постулата определяют достаточно общие геометрические свойства рельефа. Для конструктивного математического описания необходимо иметь некий способ арифметизации геометрических объектов. Поэтому необходимо ввести вспомогательный постулат, использующий некоторую числовую систему, согласованную по своим свойствам с первыми двумя постулатами. В качестве такой числовой системы выберем наиболее привычную систему вещественных чисел, тогда постулат арифметизации поверхности рельефа можно записать в следующем виде.

Третий постулат (арифметизации): рельеф это топологическое пространство с евклидовой метрикой { ( x 1 ,x 2 ,x 3 ) ∈ R 3 | | x 1 2 + x 2 1 + x 3 2 | 1/2 − R < h 0 } гомеоморфное двумерной сфере (S²), где R - множество вещественных чисел, R∈R₊, R₊ - положительные вещественные числа, h₀∈R₊ - наибольшее возможное отклонение от R, 2h₀/R<<1. Для определенности положим, что вещественные координаты точки (x₁, x₂, x₃) соответствуют декартовой прямоугольной правой системе координат с начальной точкой в центре сферы.

Последний постулат позволяет перейти от чисто геометрического представления рельефа к его представлению в виде точечного множества.

Кроме того, предположим, что рельеф не имеет "отвесных и уклонов с отрицательными углами". Это условие выразим в виде следующего постулата.

Четвертый постулат (технический): всякий луч, выходящий из центра Земли, пересекает поверхность рельефа в единственной точке.

Множество математических поверхностей s, удовлетворяющих приведенным постулатам, обозначим символом Ξ (Ξ={s} или s∈Ξ). Заметим, что используя повороты вокруг центра, некоторые поверхности s из множества Ξ можно совместить поточечно. Кроме того, не будем различать поверхности, тождественные с точностью до масштабного множителя. Такие подмножества поверхностей образуют классы эквивалентности.

Поэтому в качестве Ξ будем рассматривать множество, состоящее только из представителей классов эквивалентности s.

Так, определенное множество математических поверхностей Ξ чрезвычайно обширно. По определению в него включены все непрерывные поверхности. Все непрерывные поверхности делятся на два непересекающихся класса: класс дифференцируемых - гладких (обозначим это множество символом ) и класс всюду не дифференцируемых - негладких ({'s}) поверхностей

В картографии и геоинформатике без аргументации неявно предполагается, что рельеф Земли - гладкая функция. Действительно, картографическое изображение рельефа оперирует гладкими линиями изобат и изогипс, что возможно только для гладких функций. Пятый постулат для картографического отображения рельеф: картографический рельеф Земли представляется гладкой поверхностью.

В работе (Мандельброт Б. Фрактальная геометрия природы. - М.: Институт компьютерных исследований, 2002. - 655 с.) приведено подробное обоснование утверждения того, что рельеф Земли представляет собой фрактальную поверхность.

Фракталы можно рассматривать как множества точек, вложенные в пространство. Например, множество точек, образующих линию в обычном евклидовом пространстве, имеет топологическую размерность D_Т=1 и размерность Хаусдорфа-Безиковича D=1. Евклидова размерность пространства равна Е=3. Так как для линии D=D_T, то линия, согласно определению Мандельброта, не фрактальна, что подтверждает разумность определения. Аналогично множество точек, образующих поверхность в пространстве с Е=3, имеет топологическую размерность D_T=2 и D=2. Мы видим, что и обычная поверхность не фрактальна независимо от того, насколько она сложна. Наконец, шар, или полная сфера, имеет D=3 и D_T=3.

Центральное место в определении размерности Хаусдорфа-Безиковича и, следовательно, фрактальной размерности D занимает понятие расстояния между точками в пространстве. В общем случае при δ→0 мера M_d=∑h(δ) равна нулю или бесконечности в зависимости от выбора d - размерности меры. Размерность Хаусдорфа-Безиковича D∈R₊ множества ℑ есть критическая размерность, при которой мера M_d изменяет свое значение с нуля на бесконечность:

M d = ∑ γ ( d ) δ d = γ ( d ) N ( δ ) δ d → δ → 0 { 0, d > D ∞ , d < D .         ( 1 )

Значение M_d при d=D часто конечно, но может быть равно нулю или бесконечности. Важно учесть, при каком значении d величина M_d изменяется скачком. Заметим, что в приведенном выше определении размерность Хаусдорфа-Безиковича фигурирует как локальное свойство, так как она характеризует свойства множества точек при бесконечно малом диаметре, или размере δ пробной функции, используемой для покрытия множества. Следовательно, фрактальная размерность D может быть также локальной характеристикой множества.

В соответствии с (1) для фрактальной поверхности логарифм нормированного спектра мощности возвышений как функция логарифма длины волны шероховатостей λ должен быть линейной функцией.

Неформальная интерпретация фракталов состоит в том, что граница фрактального объекта выглядит одинаково, в каком бы масштабе их не наблюдать. Это проявление свойства масштабной инвариантности.

Фракталы можно рассматривать как множества точек, вложенные в пространство. Например, множество точек, образующих линию в обычном евклидовом пространстве, имеет топологическую размерность D_T=1 и размерность Хаусдорфа-Безиковича D=1. Евклидова размерность пространства равна Е=3. Так как для линии D=D_T, то линия, согласно определению Мандельброта (Мандельброт Б. Фрактальная геометрия природы. - М.: Институт компьютерных исследований, 2002. - 655 с.), не фрактальна, что подтверждает разумность определения. Аналогично множество точек, образующих поверхность в пространстве с Е=3, имеет топологическую размерность D_T=2 и D=2.

Мы видим, что и обычная поверхность не фрактальна независимо от того, насколько она сложна. Наконец, шар, или полная сфера, имеет D=3 и D_T=3.

Центральное место в определении размерности Хаусдорфа-Безиковича и, следовательно, фрактальной размерности D занимает понятие расстояния между точками в пространстве. В общем случае при δ→0 мера M_d=∑h(δ) равна нулю или бесконечности в зависимости от выбора d - размерности меры. Размерность Хаусдорфа-Безиковича D∈R₊ множества ℑ есть критическая размерность, при которой мера M_d изменяет свое значение с нуля на бесконечность.

Значение M_d при d=D часто конечно, но может быть равно нулю или бесконечности.

Важно учесть, при каком значении d величина M_d изменяется скачком. Заметим, что в приведенном выше определении размерность Хаусдорфа-Безиковича фигурирует как локальное свойство, так как она характеризует свойства множества точек при бесконечно малом диаметре, или размере δ пробной функции, используемой для покрытия множества. Следовательно, фрактальная размерность D может быть также локальной характеристикой множества. В действительности здесь существует несколько нюансов, заслуживающих рассмотрения. В частности, определение размерности Хаусдорфа-Безиковича позволяет покрывать множество "шарами" не обязательно одного и того же размера при условии, что диаметры всех шаров меньше δ. В этом случае d - мера есть нижняя грань, т.е. минимальное значение, получаемое при всех возможных покрытиях.

Тогда шестой постулат для рельефа Земли (апостериорный постулат физического рельефа): физический рельеф Земли адекватно представляется всюду недифференцируемой поверхностью - фракталом.

Таким образом, физическая поверхность рельефа Земли является математическим объектом из множества Ξ={'s}, тогда как картографическое представление рельефа относится к гладким функциям Ξ = { s ˜ } .

Важнейшим следствием является то, что любое сечение фрактальной поверхности будет также являться фрактальной линией. Для решения прикладных задач, важно отметить существенное различие между "вертикальными" сечениями поверхности 's и "горизонтальными". Линия пересечения 's с плоскостью, проходящей через центр 's ("вертикальное" сечение), всегда является фрактальной замкнутой одномерной простой линией. Такая линия топологически эквивалентна окружности. Другое дело "горизонтальное" сечение. Это сечение образует множество точек пересечения 's некоторой сферой с центром, соответствующим 's и с радиусом R+h, где |h|<h₀.

Множество точек такого пересечения тоже является фракталом, но этот фрактал имеет значительно более сложное устройство. Очевидно, что такое сечение может состоять из многих "замкнутых" связных изолированных между собой кусков - "береговых линий островов". Но не это главное отличие от "вертикального" сечения. "Горизонтальное" сечение приводит к линиям, значительно более сложно устроенным с топологической точки зрения. Каждый связный кусок "горизонтального" сечения топологически не эквивалентен окружности. Дело в том, что вблизи всякой точки пересечения фрактальной поверхности 's с секущей сферой число точек пересечения бесконечно. Поэтому вблизи каждой точки пересечения могут возникать "расщепления" простой линии. Таким образом, "горизонтальные" сечения 's дают некоторое множество несвязных линий, имеющих индекс ветвления, равный или больший трем. Поэтому фрактальную линию графически изобразить нельзя. Однако графически фрактал можно косвенно представить в виде некоторой бесконечной итерационной процедуры. На каждом шаге этой процедуры можно изобразить промежуточное состояние в построении фрактала. Такое промежуточное состояние называется предфракталом. Процедура построения линии, имеющей для внутренних точек индекс ветвления, равный или больший трем, поясняется примером построения линии С (называемой треугольный "ковер Серпинского") с индексом ветвления, равным или большим трем для внутренних точек, которая строится следующим образом: в равностороннем треугольнике со стороной, равной единице, проводятся средние линии, и из него выбрасываются внутренние точки треугольника, ограниченного средними линиями. Оставшееся множество состоит из треугольников первого ранга. С каждым из треугольников первого ранга проделывается та же операция: в нем проводятся средние линии и выбрасываются внутренние точки ограниченного ими треугольника. Подобным же образом поступают с каждым из девяти получившихся треугольников второго ранга и приходят к 27 треугольникам третьего ранга. Поступая так же и далее, для каждого натурального числа n получают множество, состоящее из 3" треугольников n-го ранга (фиг.1).

Оставшееся после выполнения всех этих операций множество С есть континуум. В общем случае, "горизонтальное" сечение всюду недифференцируемой поверхности представляет собой тонкую сеть с ячейками различного размера. Заметим, что "ковер Серпинского" обладает уникальным свойством: любая линия, вложимая в евклидову плоскость, вложима и в "ковер Серпинского". Данное свойство позволяет рассматривать "ковер Серпинского" в качестве универсальной линии на плоскости (Болтянский В.Г., Ефремович В.А. Наглядная топология. - М.: Наука, 1983. - 160 с.).

Одним из следствий фрактальности линии "вертикального" сечения 's, то есть отсутствия производной в любой ее точке, является ее неспрямляемость - неприменимость понятия длины для нее. Действительно, длина L гладкой плоской кривой (спрямляемой), заданной уравнением y=ƒ{x), определяется интегралом от производной: L = ∫ a b 1 + ƒ '2 ( x ) dx , но для фрактальной кривой производная не определена, следовательно, не определена и длина. Очевидно, что понятие длины не определено и для более сложно устроенной линии "горизонтального" сечения 's.

Аналогичное утверждение справедливо относительно площади поверхности для односвязной области или всей 's - площадь для фрактальных поверхностей не определена. Действительно, для кусочно-гладких функций поверхностей с кусочно гладким краем (или без края) площадь поверхности обычно определяют с помощью следующей конструкции. Поверхность разбивают на мелкие части с кусочно-гладкими границами: в каждой части выбирают точку, в которой существует касательная плоскость, и ортогонально проектируют рассматриваемую часть на касательную плоскость поверхности в выбранной точке; площадь полученных плоских проекций суммируют; наконец, переходят к пределу при все более мелких разбиениях (таких, что наибольший из диаметров частей разбиения стремится к нулю). На указанном классе поверхностей этот предел всегда существует, и если поверхность задана параметрически кусочно гладкой функцией z=ƒ(x, y) над областью D на плоскости {х, у), то площадь S выражается двойным интегралом

S = ∬ D 1 + ( d ƒ dx ) 2 + ( d ƒ dy ) 2 dxdy .   ( 2 )

Однако по определению поверхность 's всюду не дифференцируема, поэтому интеграл для площади не существует.

В первом приближении можно понимать фрактал как геометрическую фигуру, которая обладает свойством самоподобия, т.е. составленную из нескольких частей, каждая их которых подобна всей фигуре целиком. Небольшая часть фрактала содержит информацию о всем фрактале. Фракталы подобны самим себе, они похожи сами на себя на всех в любом масштабе - под каким бы увеличением не смотреть на фрактальные объекты, они будут все такими же фрагментированными и изломанными. Это свойство самоподобия приводит к тому, что для описания фрактальных мер и соотношений с необходимостью нужно использовать параметр масштаба рассмотрения фрактала. Степенная зависимость от масштаба вида (1) справедлива для:

- меры одномерного и двумерного фракталов;

- средних значений максимальных отклонений от прямой соединяющие две точки фрактала;

- соотношения периметра замкнутой фрактальной кривой и площади, ею охватываемой;

- распределение замкнутых областей при "горизонтальном" сечении 's по площади.

Свойство фрактальности проявляется в картографии в различных аспектах. Главный аспект состоит в том, что для отображения рельефа применяют длинную линейку масштабов карт. На каждом масштабе предполагается (неявно), что рельеф - гладкая поверхность. Это следует из того, что изогипсы (изобаты) - гладкие кривые. Однако рельеф одного и того же участка на картах разного масштаба различен в деталях. Причем с увеличением масштаба нет сходимости в положении изогипс (изобат), что и свидетельствует об отсутствии сходимости к некоторой гладкой поверхности. Именно это обстоятельство объясняет необходимость наличия процедуры картографической генерализации в технологии построения карт различного масштаба. Процедура генерализации осуществляется экспертным путем. В геоинформатике отсутствуют приемлемые автоматизированные алгоритмы картографической генерализации. Свойство фрактальности проявляется в математической зависимости (степенная функция) хода кривой пересеченности и используется для описания изрезанности поверхности рельефа. Алгоритм построения кривой пересеченности заключается в следующем. На карте некоторого масштаба берется произвольно, но равномерно распределенные по площади пары точек, отстоящих друг от друга на расстояние r. Определяется разность высот h каждой пары точек, и находится среднее арифметическое абсо