Способ построения спектра n-мерных неразделимых цифровых сигналов

Способ построения спектра n-мерных неразделимых цифровых сигналов

Иллюстрации

Показать все

Реферат

Изобретение относится к области обработки n-мерных цифровых сигналов и может быть использовано для анализа и синтеза фильтров, n-мерных неразделимых цифровых сигналов, практическое применение способа возможно для преобразования и обработки статических и динамических изображений, стеганографии, спектрального анализа многомерных дискретных полевых структур.

Большинство современных систем обработки, преобразования и передачи информации работает с цифровыми сигналами, при этом актуальной является задача получения спектра n-мерных неразделимых цифровых сигналов.

Известен способ получения спектра цифровых сигналов с помощью преобразования Фурье (Лайонс Р. Цифровая обработка сигналов: Второе издание. Пер. с англ. - М.: ООО «Бином-пресс», 2009, стр.63). При преобразовании Фурье происходит разложение сигнала, заданного на плоскости, образованной осями времени и амплитуды, на спектр, отображаемый на плоскости, заданной осями частоты и амплитуды, на основе базиса гармонических функций. К недостаткам преобразования Фурье можно отнести то, что в стандартном виде оно применимо к сигналам, расположенным в пространстве, образованном двумя ортогональными осями: амплитудой и временем, такие сигналы обычно называют одномерными.

Известен способ получения спектра в случае многомерного сигнала на основе ортогональных преобразований, в частности дискретное косинусное преобразование (ДКП) и его модификации, применяемые для обработки изображений (Стивен Смит. Цифровая обработка сигналов. Практическое руководство для инженеров и научных работников. Пер. с англ. Линовича А.Ю., Витязева С.В., Гусинского И.С. - М.: Додека - XXI, 2011, стр.461). Ортогональные преобразования являются линейным преобразованием евклидова векторного пространства, сохраняющем неизменным скалярное произведение векторов. В ортогональном и нормированном базисе ортогональному преобразованию соответствует ортогональная матрица. Ортогональное преобразование образует группу вращений данного евклидова пространства вокруг начала координат. В трехмерном пространстве ортогональное преобразование сводится к повороту на некоторый угол вокруг некоторой оси, проходящей через начало координат, если определитель соответствующей ортогональной матрицы равен +1. Если же этот определитель равен -1, то поворот дополняется зеркальным отражением относительно плоскости, проходящей через начало координат и перпендикулярной оси поворота. В двумерном пространстве ортогональное преобразование определяет поворот на некоторый угол вокруг начала координат или зеркальное отражение относительно некоторой прямой, проходящей через начало координат. Недостатком ДКП является то, что при его применении происходит разделение многомерного сигнала на компоненты, в результате чего утрачивается неразделимость многомерного сигнала, а полученное отображение сигнала в частотную область не во всех случаях соответствует физическому спектру сигнала.

Известен способ получения спектра как одномерного, так и многомерного цифрового сигнала путем вейвлет преобразования (Чобаноу М. Многомерные многоскоростные системы обработки сигналов. - М.: Техносфера, 2009, стр.210; Шарк Г.-Г. Применение вейвлетов для ЦОС. М., Техносфера, 2007. - 192 с., стр.14), который является наиболее близким по совокупности существенных признаков к заявляемому способу и принят в качестве прототипа. Вейвлет преобразование является способом, разбивающим сигнал на составляющие с различными частотами, каждая из которых исследуется с разрешением в подходящем масштабе. Вейвлет преобразование позволяет получить спектр n-мерного сигнала, как цифрового, так и аналогового, на основе заранее выбранных базисных n-мерных функций. В случае действительной или комплексной n-мерной функции для вейвлет преобразования выбирается анализирующая (базисная) функция g, осциллирующая относительно поверхности (в случае одномерного сигнала, около оси), образованной бесконечным множеством точек с нулевой амплитудой, что можно выразить выражением: ∫ − ∞ + ∞ g ( u ) d u = 0 , где u может быть многомерным пространством. При этом функция g(u) является быстро затухающей при u→±∞. Такую функцию g в литературе называют анализирующим, базисным или материнским вейвлетом. Взяв за основу функцию вида g ' ( u , u ' , a ) = 1 a g ( u − u ' a ) , полученную посредством сдвигов функции g(u), на величины u' и сопровождаемую сжатием (a<1) или растяжением (a>1) этой функции, получают вейвлет преобразование вида: L g f ( a , u ' ) = ∫ − ∞ + ∞ f ( u ) g ' ( u , u ' , a ) d u . Для получения спектра неразделимых сигналов при вейвлет преобразовании размерность базисного вейвлета, по которому производится разложение, должна совпадать с размерностью разделяемого на спектр сигнала. Вейвлет преобразование предоставляет свободу в выборе базисного вейвлета, с одной стороны, это является преимуществом, т.к. есть возможность выбрать наиболее оптимальную базисную функцию разложения данного сигнала на спектр, с другой стороны, недостатком: формирование библиотек вейвлетов является трудоемкой процедурой, осложненной принципиальной невозможностью выбора универсального базиса даже для сходных цифровых сигналов, например изображений.

Задачей, на решение которой направлено заявляемое изобретение является унифицированное получение спектра n-мерного неразделимого цифрового сигнала и его локализации в пространстве и (или) времени.

Указанная задача решается за счет того, что в способе построения спектра n-мерных неразделимых цифровых сигналов, основанном на одномерном вейвлет преобразовании, в ходе прямого преобразования производят последовательные, итеративные вычисления в соответствии с выражением: f_k-1=f_k-S_k; где k - номер спектральной составляющей по масштабному признаку, значение индекса k соответствует длине (периоду) взаимно перпендикулярных и параллельных элементов спектральной составляющей, f_k - остаточный сигнал (исходный сигнал f_k, где k=K - максимальное (исходное) значение индекса k), S_k - элементы исходного сигнала, отобранные по масштабному признаку, сумма всех полученных в ходе прямого преобразования спектральных составляющих S_k является исходным сигналом: f K = ∑ k = 1 K S k , каждая спектральная составляющая S_k является суперпозицией одномерного вейвлет преобразования векторов, образующих исходный сигнал по каждому из n-измерений, на базе функции типа меандр, с определенным масштабным коэффициентом по протяженности и дискретно варьирующейся амплитудой, таким образом, разложение исходного n-мерного сигнала на спектральные составляющие происходит не по выбранному заранее n-мерному базису (базисной функции), а по взаимно параллельным и перпендикулярным элементам исходного сигнала.

Сущность изобретения заключается в том, что происходит последовательное (итеративное) вычитание элементов сигнала S_k, отобранных по масштабному признаку k и расположению в пространстве, из исходного сигнала f_K, результатом каждой последовательной итерации является остаточный сигнал. Полный спектр сигнала будет получен, когда остаточный сигнал будет равен нулю. Предлагаемый способ можно выразить следующим выражением:

f k − 1 = f k − S k               ( 1 )

где: k - номер спектральной составляющей по масштабному признаку, значение k можно связать с длиной (периодом) взаимно перпендикулярных и параллельных элементов спектральной составляющей, f_k - остаточный сигнал (исходный сигнал f_k, где k=K - максимальное (исходное) значение индекса k).

Предлагаемый способ, в случае многомерного сигнала, отличается от вейвлет преобразования тем, что в нем нет заранее выбранной многомерной функции разложения, в предлагаемом способе базис фактически выбирается из элементов исходного сигнала, путем вычислений отдельно для каждой спектральной составляющей, совокупность которых образует спектр сигнала. В предлагаемом способе каждую спектральную составляющую n-мерного сигнала можно считать суперпозицией одномерного вейвлет преобразования векторов, образующих исходный сигнал по каждому из n-измерений, на базе функции типа меандр, с определенным масштабным коэффициентом по протяженности, амплитуда элементов, образующих спектральную составляющую, может дискретно варьироваться. Предлагаемый способ, так же как и вейвлет преобразование, в отличие от преобразования Фурье позволяет получить отображение сигнала в фазовое пространство, т.е. позволяет получить четкую привязку спектральных особенностей сигнала к пространству и (или) времени, стоит заметить, что отобразить одномерный сигнал на фазовую плоскость позволяет оконное преобразование Фурье.

Для раскрытия способа необходимо уточнить обозначения измерений пространств, в которых применим рассматриваемый способ. Будем использовать понятия векторного поля и зададим функции координат положения: f ( x 1 ) - для одномерного; f ( x 1 , x 2 ) - для двухмерного; f ( x 1 , x 2 , x 3 ) - для трехмерного; … f ( x 1 , x 2 , x 3 , … , x n ) - для n-мерного. Координаты вектора поля в указанной точке: { ν 1 } - для одномерного; { ν 1 , ν 2 } - для двухмерного; { ν 1 , ν 2 , ν 3 } - для трехмерного; … { ν 1 , ν 2 , ν 3 , … ν p } - для p-мерного. В частном случае координаты положения могут соответствовать пространственно-временным координатам. При этом в практике обработки цифровых сигналов координаты положения и направлений вектора поля часто имеют различную размерность. Например, если в качестве сигнала рассматривать сигнал, отображаемый на дисплее осциллографа, то координата времени будет соответствовать координате положения (f(t) - одномерное), координате вектора поля будет соответствовать амплитуда ( { ν 1 } - одномерное). В данном случае координаты положения и координаты вектора поля имеют одинаковую размерность, но различные единицы измерения. Следующие примеры описывают случаи, когда размерности положения и вектора поля различны. Положение каждого пикселя цифрового изображения, сформированного на двумерной плоскости, характеризуется двумя координатами f ( x 1 , x 2 ) , в случае представления изображения в виде оттенков серого цвета, мы будем иметь одномерное пространство для вектора поля { ν 1 } , в случае цветного изображения мы можем разделить спектр по базису RGB, получив трехмерное пространство для вектора поля {R, G, B}.

Особенностью большинства многомерных сигналов является неразделимость, т.е. невозможно применить базис меньшей мерности, чем мерность сигнала, не разделяя исходный сигнал на составляющие размерности базиса. В этом смысле существенным прорывом стало использование многомерных вейвлетов на базе выбранных функций-всплесков, позволяющих сохранять спектральную неразрывность сигналов. Предлагаемый способ предоставляет возможность разделения многомерных сигналов, при различных соотношениях размерностей положения и вектора поля, на спектральные составляющие, используя базисы, являющиеся элементами исходного сигнала.

Введем понятие элементарный всплеск - это дискретная структура, имеющая размерность положения, равную размерности исходного сигнала, отличную от нуля амплитуду (высоту). В направлении положения, по которому происходит выделение элементарного всплеска, его протяженность может иметь любое отличное от нуля значение, но не более размера исходного сигнала в данном направлении. По другим направлениям положения размеры элементарного всплеска равны единице дискретизации соответствующих направлений положения.

Разделение исходного сигнала f_K на спектральные составляющие происходит, начиная с самых протяженных (долгопериодических) элементарных всплесков, последовательно по всем направлениям положения. В каждой последующей итерации в соответствии с выражением (1) протяженность элементарного всплеска имеет значение на единицу меньше, чем в предыдущей. При выделении из исходного сигнала взаимно перпендикулярных элементарных всплесков учитывается принцип суперпозиции волн, т.е. сложения их амплитуд в месте пересечения. По этой причине последовательность обхода направлений положения, для выполнения условия однозначности разложения, должна быть одинаковой для каждой спектральной составляющей. Каждая спектральная составляющая S_k является совокупностью (суммой) элементарных всплесков протяженностью k, выделенных в остаточном сигнале f_K.

Заявляемый способ иллюстрируется фиг.1-18.

Фиг.1 - последовательное разложение на спектр сигнала с одномерным пространством положения и одним вектором поля предлагаемым способом.

Фиг.2 - последовательное разложение на спектр сигнала с двумерным положением и одномерным вектором поля предлагаемым способом. Вектор поля направлен вверх от плоскости, образуемой осями x₁, x₂. В соответствии с выражением (1) исходный сигнал f₁₀ и остаточные составляющие сигнала f₄, f₁, f₀, причем f₀ - нулевой остаток. В данном случае выделение спектральных составляющих S₅, S₂, S₁ осуществляется по протяженности всплесков, причем отдельно выделяются всплески сначала в направлении x₁, затем в направлении x₂. Следует обратить внимание, что максимальная протяженность всплеска соответствует максимальному размеру (числу элементов дискретизации) разделяемой на спектр области из направлений положения. Для случая, приведенного на фиг.2, максимальный размер соответствует направлению X) с числом дискретов 10. Это означает, что максимальная протяженность всплесков возможна только вдоль оси x₁, по оси x₂, максимальная длина всплесков, ограничена размером шесть. Для случая, рассмотренного ранее, фиг.1, максимальная протяженность всплесков ограничена числом элементов дискретизации по оси x, т.е. двенадцатью.

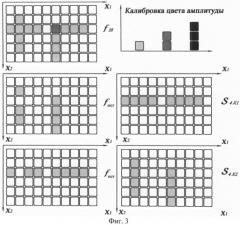
Фиг.3 - возможные неоднозначности разложения при несогласованном выборе обхода направлений положения. При сложении взаимно перпендикулярных всплесков, в силу суперпозиции, в случае пересечения область пересечения является суммой пересекающихся всплесков. Поэтому при последовательном вычитании перпендикулярных всплесков может возникнуть неоднозначность разложения. Таким образом, необходимо строго выполнять покоординатную последовательность вычитания перпендикулярных всплесков, т.е. придерживаться ранее выбранной последовательности.

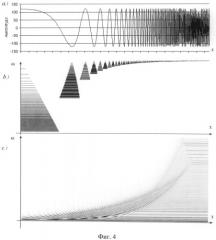
Фиг.4 - сигнал (а) и диаграммы на фазовой плоскости, полученные методом преобразования Фурье в движущемся окне (с) и предлагаемым способом (b). Красным цветом обозначены всплески с положительной амплитудой, синим - с отрицательной.

Фиг.5 - сигнал (а) и диаграммы на фазовой плоскости, полученные методом преобразования Фурье в движущемся окне (с) и предлагаемым способом (b).

Фиг.6 - спектрограмма сигнала (а) фиг.5, полученная при помощи предлагаемого способа.

Фиг.7 - диаграмма плотности сигнала (а) фиг.5 на фазовой плоскости, полученная при помощи предлагаемого способа.

Фиг.8 - спектрограмма сигнала (а) фиг.5, полученная при помощи преобразования Фурье по всему ряду данных.

Фиг.9 - сигнал (а) и диаграммы на фазовой плоскости, полученные методом преобразования Фурье в движущемся окне (с) и предлагаемым способом (b).

Фиг.10 - спектрограмма сигнала (а) фиг.9, полученная при помощи предлагаемого способа.

Фиг.11 - диаграмма плотности сигнала (b) фиг.9 на фазовой плоскости, полученная при помощи предлагаемого способа.

Фиг.12 - спектрограмма сигнала (а) фиг.9, полученная при помощи преобразования Фурье по всему ряду данных.

Фиг.13 - исходное двумерное поле, заданное функцией

f ( x 1 , x 2 ) = S i n ( x 1 3 ) + S i n ( x 2 3 ) ,   x 1 , x 2 ∈ [ 0 , 1 2 π 5 ] .

Фиг.14 - частичные результаты спектрального разложения двухмерного сигнала предлагаемым способом, в названии файла содержится номер спектральной составляющей, соответствующий протяженности элементарных всплесков. Очевидно смещение плотности в спектральных составляющих в соответствии с изменением частоты в исходном поле фиг.13.

Фиг.15 - исходное двумерное поле, заданное функцией

f ( x 1 , x 2 ) = S i n [ x 1 2 + x 2 2 ] ,   x 1 , x 2 ∈ [ − 7 7 π 5 ,   7 7 π 5 ] .

Фиг.16 - частичные результаты спектрального разложения двухмерного сигнала фиг.15 предлагаемым способом, в названии файла содержится номер спектральной составляющей, соответствующий протяженности элементарных всплесков.

Фиг.17 - распределение плотности ненулевых элементов в спектральной составляющей, в зависимости от протяженности всплеска для всплесков вдоль оси x₁. Плотность ненулевых элементов в спектральной составляющей рассчитывалась как число ненулевых элементов в поле спектральной составляющей, отнесенное к полному числу (площади) всей спектральной составляющей. Очевидно значительное повышение плотности, соответствующее выделению всплесками радиальных волн фиг.15 и фиг.16.

Фиг.18 - распределение плотности ненулевых элементов в спектральной составляющей, в зависимости от протяженности всплеска для всплесков вдоль оси x₂. Плотность ненулевых элементов в спектральной составляющей рассчитывалась как число ненулевых элементов в поле спектральной составляющей, отнесенное к полному числу (площади) всей спектральной составляющей. Очевидно значительное повышение плотности, соответствующее выделению всплесками радиальных волн фиг.15 и фиг.16.

Для реализации предлагаемого способа необходимо применить последовательную совокупность действий, отвечающую всем признакам алгоритма.

Порядок последовательности действий способа строго определен и детерминирован.

Условия осуществления действий способа определяются цифровым форматом исходного n-мерного сигнала, являющимся входными данными для алгоритма реализации способа.

Осуществление изобретения в самом простом случае: одномерного пространства положения и одного вектора поля для дискретного сигнала фиг.1. Частным случаем такого сигнала является измерение некоторой одномерной величины (например, тока) во времени.

В соответствии с выражением (1) на диаграммах обозначены остаточные составляющие сигнала f₃, f₂, f₁, f₀ и спектральные составляющие S₄, S₃, S₂, S₁. Сигнал f₁₂ - является исходным сигналом, а f₀ - нулевым остатком. По причине отсутствия в спектре составляющих с номерами (длиной) 12…5 их диаграммы не приведены, т.к. спектральные составляющие с соответствующими номерами равны нулю, и соответственно неизменны значения остаточного сигнала. Данный пример очень показателен с точки зрения практических результатов предлагаемого способа:

- если положить, что ось x соответствует времени, то сумма S₄, S₃, S₂, S₁ в каждый отдельный момент времени позволяет получить спектр сигнала, при этом не требовалось производить вычисления спектра в сдвигаемом окне, как это требуется при Фурье преобразовании для получения отображения сигнала на фазовую плоскость;

- позволяет охватить сразу весь сигнал или любой выбранный фрагмент, причем результатами способа является набор спектральных составляющих, в совокупности представляющих отображение сигнала в фазовом пространстве, в частном случае в фазовой плоскости (t, ω).

Результаты данного спектрального преобразования практически соответствуют результатам вейвлет преобразования на базе единичного всплеска типа меандр. При переходе к большим мерностям принципиальное различие подходов становится очевидным. Рассмотрим случай двумерного положения ( f ( x 1 , x 2 ) ) и одномерного вектора поля { ν 1 } фиг.2.

Вектор поля направлен вверх от плоскости, образуемой осями x₁, x₂. В соответствии с выражением (1) исходный сигнал f₁₀ и остаточные составляющие сигнала f₄, f₁, f₀, причем f₀ нулевой остаток. В данном случае выделение спектральных составляющих S₅, S₂, S₁ осуществляется по протяженности всплесков, причем отдельно выделяются всплески сначала в направлении x₁, затем в направлении x₂.

Следует обратить внимание, что максимальная протяженность всплеска соответствует максимальному размеру (числу элементов дискретизации) разделяемой на спектр области из направлений положения. Для рассматриваемого случая фиг.2 максимальный размер соответствует направлению x₁, с числом дискретов 10. Это означает, что максимальная протяженность всплесков возможна только вдоль оси x₁, по оси x₂ максимальная длинна всплесков ограничена размером шесть. Для случая, рассмотренного ранее, фиг.1, максимальная протяженность всплесков ограничена числом элементов дискретизации по оси x, т.е. двенадцатью.

При разложении на перпендикулярные составляющие учитывается принцип суперпозиции волн, например, в областях, где перпендикулярные волны пересекаются, происходит сложение их амплитуд.

Обобщенный алгоритм формирования спектральных составляющих, позиционируемый как реализация предлагаемого способа (прямое преобразование) для N-мерного пространства положения x₁, x₂…x_N и одномерного вектора поля (алгоритм 1).

1. На поле f_k выбирают начальное значение K = max ( x 1 , x 2 … x N ) как максимальное значение определенности (т.е. наличия значений) сигнала в направлениях положения. В следующих пунктах алгоритма последовательно в порядке х₁, х₂…x_N выделяют перпендикулярные и параллельные элементарные всплески.

2. Задают начальное значение координаты выделения элементарных всплесков n=1.

3. Проверяют, если протяженность поля в выбранном направлении x_n меньше k, то переходим к пункту 4, иначе переходят к пункту 6.

4. Выделяют вдоль направления x_n элементарные всплески протяженностью k, всплеск должен удовлетворять следующим условиям:

- границами всплеска считаются элементы, имеющие либо нулевое, либо отличное по знаку (в случае знакопеременного сигнала) значение от значений всплеска;

- элементарный всплеск имеет амплитуду, которая определяется как минимальное значение между его границами;

- у элементарного всплеска единичная протяженность по всем направлениям положения кроме x_n.

5. Если в пункте 4 были локализованы элементарные всплески, то вычитают их из остаточного сигнала f_k и добавляют к спектральной составляющей S_k в соответствии с выражением f_k-1=f_k-S_k.

6. Если значение n меньше N, то n=n+1, и переходят к пункту 3, иначе переходят к пункту 7.

7. Если значение k больше 1, то k=k-1, и переходят к пункту 2, иначе окончание алгоритма.

Результатом вычисления по алгоритму 1 является совокупность спектральных составляющих, образованных суммами перпендикулярных и параллельных элементарных всплесков в направлениях x₁, x₂…x_N. Таким образом, разложение исходного сигнала f m a x ( x 1 , x 2 … x N ) осуществляется по функциям «суммы элементарных всплесков», содержащихся в самом исходном сигнале. Иллюстрация к алгоритму 1 для двумерного сигнала на фиг.1.

Спектральные составляющие, полученные предлагаемым способом, сами имеют размерность исходного сигнала: положения p ( x 1 , x 2 , … , x n ) и одномерного вектора поля { ν 1 } . При разложении в спектр предлагаемым способом для многомерных полевых структур с размерностью поля { ν 1 , ν 2 , ν 3 , … ν n } расчет спектральных составляющих необходимо производить отдельно для каждого направления ν₁, ν₂, ν₃, …ν_p, получая отдельные наборы спектральных составляющих для каждого направления поля. Полученные наборы спектральных составляющих можно рассматривать как векторные составляющие спектра поля и объединять путем сложения векторных компонент, перенося в пространство, имеющее размерность исходного поля.

Однозначность разложения определяется соблюдением условий последовательности действий. При сложении взаимно перпендикулярных всплесков в силу суперпозиции, в случае пересечения, область пересечения является суммой пересекающихся всплесков фиг.3. Поэтому при последовательном вычитании перпендикулярных всплесков без соблюдения выбранной заранее покоординатной последовательности может возникнуть неоднозначность разложения. Таким образом, необходимо строго выполнять покоординатную последовательность вычитания перпендикулярных всплесков, т.е. придерживаться заранее выбранной последовательности (алгоритм 1, пункт 2 и пункт 6).

При анализе рассматриваемого способа получения спектральных составляющих в многомерном пространстве очевидны принципиальные отличия от вейвлет преобразования. При использовании рассматриваемого способа для получения спектра каждый элемент каждой спектральной составляющей S_k сам является некоторой выделенной частью исходного сигнала и таким образом идеально подходит для формирования исходного сигнала f_K.

Обобщенный алгоритм формирования исходного сигнала из спектральных составляющих, позиционируемый как реализация способа (обратное преобразование) для N-мерного пространства положения х₁, х₂…x_N и одномерного вектора поля (алгоритм 2).

Исходный сигнал f m a x ( x 1 , x 2 … x N ) является суммой полученных спектральных составляющих S_k по алгоритму 1, поэтому его можно определить как:

f m a x ( x 1 , x 2 … x N ) = ∑ k = 1 m a x ( x 1 , x 2 … x N ) S k .               ( 2 )

В соответствии с выражением (2) получение исходного сигнала осуществляется суммированием спектральных составляющих S_k. Каждая спектральная составляющая является массивом данных размерности N и размера (по направлениям) исходного сигнала, суммирование осуществляется по каждому элементу спектральных составляющих S_k, имеющих одинаковые координаты. Таким образом, значение каждого элемента исходного сигнала f max ( x 1 , x 2 … x N ) можно определить как:

f max ( x 1 , x 2 … x N ) [ x 1 ' , x 2 ' , … x N ' ] = ∑ k = 1 max ( x 1 , x 2 … x N ) S k [ x 1 ' , x 2 ' , … x N ' ] ,     ( 3 )

где: x 1 ' , x 2 ' , … x N ' - соответствующие координаты элемента дискретного сигнала и спектральной составляющей.

Порядок вычислительной сложности O(X) алгоритма, реализующего предлагаемый способ, может быть оценен по следующему выражению:

{ O ( X ) = N ⋅ ( N − 1 ) ⋅ [ k x i 2 + k x i 2 ] , N > 1           ( 4 )

где: N - размерность положения x₁, x₂, …x_N, k x i 2 - размер сигнала в направлении x_i.

Для одномерного сигнала N=1 выражение имеет вид:

O ( X ) = [ k 2 + k 2 ] .                 ( 5 )

Порядок вычислительной сложности для дискретного преобразования Фурье (ДПФ) может быть оценен:

O ( Д П Ф ) = 2 k 2 ,                 ​   ( 6 )

где: k - размер массива данных.

Для быстрого преобразования Фурье (БПФ):

O ( Д П Ф ) = k L o g 2 ( k ) .                 ​ ( 7 )

При этом все операции при вычислениях по предлагаемому способу над дискретным сигналом производятся на кольце целых чисел, на практике это означает, что алгоритм может быть полностью реализован на элементарных целочисленных операциях процессора. Преобразование Фурье производится на поле комплексных чисел, это означает необходимость применения специальных функций вычислительных операций либо математического сопроцессора, следовательно, потребление значительных вычислительных ресурсов.

Возможность реализации предлагаемого способа на кольце целых чисел позволяет позиционировать способ как достаточно легко реализуемый только аппаратными средствами. Предлагаемый способ может быть практически реализован программными средствами на базе ЭВМ или полностью аппаратными средствами на базе логических элементов, в частности ПЛИС.

Таким образом, предлагаемый способ позволяет путем последовательных преобразований получать спектр n-мерных неразделимых цифровых сигналов, исключая процедуру выбора специальных базисов разложения, результатами способа является набор спектральных составляющих, в совокупности представляющих отображение сигнала в фазовом пространстве.

Способ построения спектра n-мерных нераздел