Способ стереосъемки рельефа дна акватории и устройство для его осуществления

Способ стереосъемки рельефа дна акватории и устройство для его осуществления

Иллюстрации

Показать все

Реферат

Изобретение относится к области гидрографии и может быть использовано для стереосъемки рельефа дна акватории гидроакустическим средством (ГАС), а также поиска подводных объектов, расположенных на поверхности дна акватории.

Известен способ стереосъемки рельефа дна акватории (патент US №3781775, кл. 340/3R [1]), который включает перемещение носителем двух ГАС по заданным галсам, антенны которых разнесены в горизонтальной плоскости на заданную величину, определение составляющей базиса стереообзора, при этом антенны ГАС излучают зондирующие импульсы, которые по мере распространения последовательно облучают поверхность дна акватории, принимают отраженные от поверхности дна сигналы, измерение времени от момента излучения каждого зондирующего импульса до момента приема каждого отраженного от поверхности дна импульса с непрерывной регистрацией их интенсивности, определение параллактического смещения между соответствующими записями изображений рельефа дна акватории или затонувших объектов на эхограммах двух самописцев ГАС, возникающего за счет разноса их антенн, и их геодезических координат и составление по полученным данным стереокарты рельефа дна акватории.

Известный способ стереосъемки микрорельефа дна акватории ([1]) реализован посредством устройства, содержащего два ГАС, которые включают функционально соединенные две акустические антенны, два приемопередатчика, два электромеханических регистратора, фотограмметрический прибор, приемник космической навигационной системы, блок вычисления параллактического смещения между записями изображений рельефа на эхограммах двух самописцев ГАС и их геодезических координат и отображения стереокарты рельефа дна поверхности акватории.

При этом вычисление параллактического смещения вычисляют как разность параллаксов (ΔР) двух точек, разнесенных по вертикали в соответствии с зависимостью

Δ P = { [ g + ( l - d ) ] - [ g + d ] } - { [ g H + ( l - d ) ] - [ g H - d ] } , ( 1 )

где g = Z B - коэффициент формы рельефа;

Z - глубина нижней точки;

В - базис стереообзора;

d = d ' B - нормированная позиция нижней точки;

Н=i-h - условное превышение;

h = h ' z - нормированное превышение верхней точки над нижней,

где h' - превышение нижней точки.

Недостатками известного способа стереосъемки рельефа дна акватории и устройства для его осуществления, исходя из их сущности, являются:

- трудоемкость вычисления ΔР по формуле (1);

- наличие погрешности определения ΔР от углов крена, дифферента и рыскания носителя ГАС;

- зависимость стереообзора от величины базиса, что ограничивает глубину стереосъемки на акватории при неизменном базисе.

Кроме того, при решении прикладных задач, например, связанных со строительством подводных трубопроводов на больших глубинах, весьма важным является, чтобы все формы рельефа или искусственные подводные объекты были идентифицированы в ходе батиметрической инструментальной съемки по измеренным глубинам звуковыми сигналами, формируемыми, в частности, высокочастотными многолучевыми эхолотами для получения детальной картины рельефа дна.

При съемке рельефа дна многолучевыми эхолотами глубины в горизонтальной плоскости измеряются (формируются) с определенной дискретностью, которая связана с углом направления луча, способом формирования лучей, частотой многолучевого эхолота, разрешающей способностью формирования луча. Причем эта дискретность является в общем случае функцией глубины L=f(H).

Например, для высокочастотного многолучевого эхолота типа ЕМ 100, используемого при проведении батиметрической инструментальной съемки при проектных работах при прокладке подводных магистральных трубопроводов для транспортировки углеводородов, горизонтальная дискретность распределения глубин на равном расстоянии в мелководном режиме равна L=6,3% Н, где Н - глубина, при распределении глубин на равных углах это расстояние на боковых лучах увеличивается по сравнению с центральными лучами. Это приводит к тому, что при увеличении глубины съемки возможен пропуск опасной для трубопровода формы рельефа. С точки зрения проектирования параметров трубопровода, пересечение трубопроводом такой опасной формы приводит к увеличению свободного пролета трубы и увеличению нагрузки в точке касания трубы с рельефом опасной формы. При проектировании параметров трубопровода основой является батиметрический профиль, и отсутствие фиксации на профиле опасной глубины в реальных условиях может приводить к превышению допустимых нагрузок на трубу и, соответственно, к ее повреждению, поэтому задача определения вероятности пропуска опасной формы рельефа при проведении батиметрической съемки является весьма актуальной.

Аналогичная проблема характерна и для ГАС, выполненной в виде гидрографического эхографа бокового обзора типа ГЭБО - 100, предназначенного для производства гидрографических работ в целях выявления характера рельефа дна или поиска подводных объектов, представляющих навигационную опасность (Инструкция по использованию гидрографического эхографа ГЭБО - 100. Министерство обороны союза ССР, Главное управление навигации и океанографии. Адмиралтейский №9125, 1985, с.5-45 [2]).

При этом восстановление формы рельефа дна по дискретным измерениям выполняют путем интегральных преобразований на основе комбинаторного метода анализа геопространственных полей по точечным измерениям. При этом одной из важных подготовительных задач является задача построения цифровой модели рельефа (ЦМР). Эта задача осуществляется либо по картографическим материалам, либо по исходным данным измерений глубин. В последнем случае, для получения ЦМР применяют вычислительные процедуры, встроенные в программные пакеты геоинформационных систем (ГИС). Однако ГИС технологии не позволяют получить логически обоснованные ЦМР. Это обусловлено двумя основными обстоятельствами.

Первое обстоятельство связано с искажениями смысла при использовании математических терминов в геоинформатике. Эта логическая ошибка относится к софистическим приемам, основанным на подмене понятий. Например, в геоинформатике используются математические методы интерполяции и аппроксимации, при этом как интерполируемая функция неизвестна, так неизвестен и класс аппроксимируемых функций. Тогда как в математике эти термины применимы либо к заданной функции или к заданному классу функций. Другими словами, в условиях геоинформатики применение этих терминов, равно как и соответствующих им математических методов, логически некорректно.

Второе обстоятельство связано с тем, что используются алгоритмы, свойства которых неадекватно соответствуют свойствам рельефа. Например, эвристический метод интерполяции - крикинг, в основе использует искусственное предположение о рельефе как стационарной случайной функции, что противоречит одному из постулатов теории измерений, который утверждает, что измеряемая величина не может быть случайной (Лячнев В.В., Сирая Т.Н., Довбета Л.И. Основы теории измерений физических величин. - СПб.: Изд-во СПбГЭТУ "ЛЭТИ", 2004. - 310 с.). Напротив, другой метод - триангуляции - не учитывает основное свойство рельефа - изменчивости. Триангуляция учитывает только свойство взаимного расположения координат точек, а значения высот (глубин) в них не использует. Рельеф в виде ЦМР описывается некоторой областью поверхности в фиксированном пространственном масштабе. При этом остаются неизвестным и алгоритмы получения ЦМР, и алгоритмы согласования ЦМР с другими масштабами этой территории или граничащими с ней. При таком подходе полностью отсутствует представление о рельефе как единой целостной структуре, включающей все масштабы геоморфологичеких форм на всей поверхности Земли. В этих условиях построить логически корректную технологию автоматизированной обработки гидрографических измерений для построения рельефа дна практически невозможно.

Разрешение этой проблемной ситуации требует разработки описания рельефа как единого формализованного объекта с явным перечислением его свойств. Только наличие такой информации позволит осуществить разработку конструктивной автоматизированной технологии построения рельефа дна по гидрографическим измерениям.

Выявленные недостатки присущи и другим аналогам (патент RU №2292062 С2, 20.01.2007 [3], патент RU №2272303 С1, 20.03.2006 [4], патент RU №2340916 С1, 10.12.2008 [5], патент RU №2326408, 10.06.2008 [6], патент RU №1829019 A1, 27.07.1993 [7], патент JP №10325871 A, 08.12.1998 [8], патент JP №94372890 A, 25.12.1992 [9]).

Задачей предлагаемого технического решения является повышение достоверности восстановления рельефа дна при выполнении стереосъемки микрорельефа дна акватории посредством ГАС.

Поставленная задача решается за счет того, что в способе стереосъемки рельефа дна акватории, включающем перемещение гидроакустического средства по заданным галсам на акватории посредством гидрографического судна, оснащенного измерителями скорости и курса движения, измерителем глубины, приемоиндикатором спутниковой навигационной системы и/или приемоиндикатором радионавигационной системы, соединенных с судовой ЭВМ, при этом посредством антенн гидроакустического средства, выполненного в виде гидрографического эхографа бокового обзора, излучают зондирующие импульсы, которые по мере их распространения последовательно облучают поверхность дна акватории, принимают отраженные от поверхности дна сигналы, измерение времени от момента излучения каждого зондирующего импульса и непрерывную регистрацию их интенсивности, определение параллактического смещения между соответствующими записями изображений рельефа дна акватории на эхограммах двух самописцев и их геодезических координат и по полученным данным составление стереокарты рельефа дна акватории, предварительно формируют цифровую карту рельефа дна акватории по архивным данным с выделением опасных форм рельефа, антенны гидроакустического средства размещают в вертикальной плоскости по одному борту гидрографического судна, излучение зондирующих импульсов выполняют синхронно для каждой антенны на разных частотах, отраженные от поверхности дна сигналы принимают по направлениям, образующим с вертикальной плоскостью, перпендикулярной с диаметральной плоскостью гидрографического судна, два симметричных заданных угла, по полученным дискретным измерениям строят цифровую карту рельефа дна, выполняют топологический анализ рельефа, при этом формируют граф Кронрода-Риба и комплексы Морса-Смейла для каждой кусочно-линейной поверхности, выполняют оценку фрактальных параметров рельефа, в устройство для осуществления способа стереосъемки рельефа дна акватории, выполненное в виде гидроакустического средства, содержащего функционально соединенные две приемоизлучающие антенны, два электромеханических регистратора, фотограмметрический прибор, блок определения параллактического смещения между соответствующими записями изображений рельефа на самописцах электромеханических регистраторов, стереокарту рельефа дна акватории съемки и информационно соединенного с судовой ЭВМ, дополнительно введены функциональный блок, своими входами соединенный с выходами двух электромеханических регистраторов, а своим входом-выходом соединенный с входом-выходом судовой ЭВМ, инерциальный измерительный модуль, соединенный с приемоиндикатором спутниковой навигационной системы, электронная картографическая навигационная система, соединенная своим входом-выходом с входом-выходом судовой ЭВМ, две приемоизлучающие антенны установлены на шасси, снабженные измерительным инерциальным модулем, соединенным с приемоиндикатором спутниковой навигационной системы.

Новые отличительные признаки предлагаемого технического решения заключаются в том, что предварительно формируют цифровую карту рельефа дна акватории по архивным данным с выделением опасных форм рельефа, антенны гидроакустического средства размещают в вертикальной плоскости по одному борту гидрографического судна, излучение зондирующих импульсов выполняют синхронно для каждой антенны на разных частотах, отраженные от поверхности дна сигналы принимают по направлениям, образующим с вертикальной плоскостью, перпендикулярной с диаметральной плоскостью гидрографического судна, два симметричных заданных угла, по полученным дискретным измерениям строят цифровую карту рельефа дна, выполняют топологический анализ рельефа, при этом формируют граф Кронрода-Риба и комплексы Морса-Смейла для каждой кусочно-линейной поверхности, выполняют оценку фрактальных параметров рельефа, в устройство для осуществления способа стереосъемки рельефа дна акватории, выполненное в виде гидроакустического средства, содержащего функционально соединенные две приемоизлучающие антенны, два электромеханических регистратора, фотограмметрический прибор, блок определения параллактического смещения между соответствующими записями изображений рельефа на самописцах электромеханических регистраторов, стереокарту рельефа дна акватории съемки и информационно соединенного с судовой ЭВМ, дополнительно введены функциональный блок, своими входами соединенный с выходами двух электромеханических регистраторов, а своим входом-выходом соединенный с входом-выходом судовой ЭВМ, инерциальный измерительный модуль, соединенный с приемоиндикатором спутниковой навигационной системы, электронная картографическая навигационная система, соединенная своим входом-выходом со входом-выходом судовой ЭВМ, две приемоизлучающие антенны установлены на косвенной стабилизируемой платформе, снабженной измерительным инерциальным модулем, соединенным с приемоиндикатором спутниковой навигационной системы.

При перемещении гидрографического судна, оснащенного ГАС с установкой двух приемопередающих антенн в вертикальной плоскости по одному борту гидрографического судна, с излучением зондирующих импульсов синхронно для каждой антенны на разных частотах, прием отраженных от поверхности дна сигналов по направлениям, образующим с вертикальной плоскостью, перпендикулярной с диаметральной плоскостью гидрографического судна, два симметричных заданных угла позволяют последовательно освещать каждый элемент рельефа дна сначала одним, а затем другим акустическим лучом, что и обуславливает возникновение продольного параллакса в направлении перемещения гидрографического судна. При этом роль линейного базиса играет угловой раствор характеристики направленности антенн (акустических лучей), который является угловым базисом стереобзора.

Предварительное формирование цифровой карты рельефа заданной акватории по архивным данным с выделением опасных форм рельефа позволяет исключить вероятность пропуска опасной формы рельефа при проведении батиметрической съемки.

Применение методов описания рельефа с помощью функций Морса, графов Кронрода-Риба и комплексов Морса-Смейла обеспечивает возможность:

- топологического кодирования форм рельефа;

- картографической генерализации;

- распознавания геоморфологических объектов;

- формальной классификации геоморфологических объектов;

- замощения поверхности рельефа семейством параметризованных (полиномиальных) функций, заданных на клетках Морса-Смейла;

- иерархически оценивать степень сходства двух карт рельефа, представляющих одну область, в одном или разных масштабах;

- оценки достоверности выделенных форм рельефа с учетом погрешности и мощности исходной информации;

- оценки степени достаточности набора точечных измерений для восстановления рельефа с заданной подробностью.

Для осуществления перечисленных возможностей в устройство для осуществления способа введен функциональный блок, реализующий следующий перечень основных алгоритмов:

- восстановления рельефа по дискретным измерениям с использованием топологических;

- формирования графа Кронрода-Риба для кусочно-линейной поверхности;

- формирования комплексов Морса-Смейла для кусочно-линейной поверхности;

упрощения кусочно-линейной поверхности с использованием полученных для нее структур графа Кронрода-Риба и комплексов Морса-Смейла;

- оценку фрактальных параметров рельефа на основе заданных структур графа Кронрода-Риба и комплексов Морса-Смейла, что позволяет реализовать восстановление сложных конструкций рельефа, например "пещер", "тоннелей" и т.п. на основе положения теории гомологии.

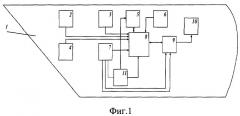
Сущность предлагаемого технического решения поясняется чертежами (фиг.1, 2, 3). Фиг.1. Блок-схема устройства для реализации способа стереосъемки рельефа. Блок-схема содержит гидрографическое судно 1, оснащенное измерителем скорости 2, курсоуказателем 3, измерителем глубины 4, приемоиндикаторами 5 и 6 спутниковой и радионавигационной систем соответственно, гидроакустическое средство, выполненное в виде гидрографического эхографа 7 бокового обзора, судовую ЭВМ 8, функциональный блок 9, электронную картографическую навигационную информационную систему (ЭКНИС) 10, инерциальный измерительный модуль 11.

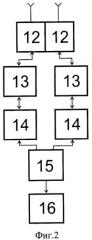
Фиг.2. Блок-схема гидрографического эхографа 6 бокового обзора. Блок-схема включает функционально соединенные две приемоизлучающие антенны 12, два приемопередатчика 13, два электромеханических регистратора 14, фотограмметрический прибор 15, блок 16 определения параллактического смещения между соответствующими записями изображений рельефа дна на самописцах электромеханических регистраторов 14.

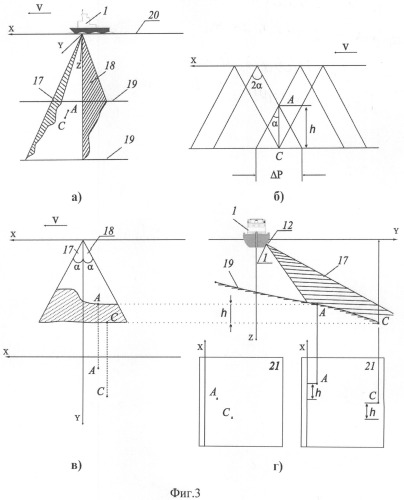
Фиг.3 (а, б, в, г). Схема бокового обзора дна. Позициями обозначены: гидрографическое судно 1, направления лучей 17, 18, формируемых соответственно приемоизлучающими антеннами 12, дно 19 акватории съемки, расположение съемочного галса 20, стереокарта 21, V - скорость гидрографического судна 1, x, у, z - координатные оси, А и С - произвольные точки на дне акватории, Р - параллакс произвольных точек А и С на эхограммах электромеханических регистраторов 14, X_A, X_C и X A ' , X C ' - абсциссы точек А и С, снятые с эхограмм электромеханических регистраторов 14, соответственно посредством фотограмметрического прибора 7, α - угол между вертикалью и направлением на точку отражения, h - относительное превышение точек А и С.

Гидроакустическое средство для съемки рельефа дна выполнено в виде гидрографического эхографа 6 бокового обзора и включает функционально соединенные две приемоизлучающие антенны 12, два электромеханических регистратора 14, фотограмметрический прибор 15, блок 16 определения параллактического смещения между соответствующими записями изображений рельефа на самописцах электромеханических регистраторов 14 со стереокартой рельефа дна акватории съемки и информационно соединенного с судовой ЭВМ 8, функциональный блок 9, который своими входами соединен с выходами двух электромеханических регистраторов 14, а своим входом-выходом соединенный с входом-выходом судовой ЭВМ 8, две приемоизлучающие антенны 12 установлены на шасси, снабженных измерительным инерциальным модулем 11, соединенным с приемоиндикатором 5 спутниковой навигационной системы.

Аналогом гидрографического эхографа 6 бокового обзора является гидрографический эхограф ГЭБО-100 [2].

Измеритель скорости 2, курсоуказатель 3, измеритель глубины 4, приемоиндикаторы 5 и 6 спутниковой и радионавигационной систем являются штатными средствами гидрографического судна 1 для обеспечения решения навигационных задач и батиметрической съемки.

Инерциальный измерительный модуль 11 представляет собой бесплатформенный инерциальный измерительный модуль, построенный на волоконно-оптических гироскопах и миниатюрных акселерометрах и микровычислителе, установленных в едином корпусе и соединенных с приемоиндикатором 5 спутниковой навигационной системы GPS/ГЛОНАСС, аналогом которого является миниатюрная интегрированная инерциальная/спутниковая система навигации и ориентации типа «Мини-навигация-1» (ОАО «Концерн «ЦНИИ «Электроприбор») и предназначен для выработки углов качки и рыскания, вертикальной качки и составляющих угловой скорости как гидрографического судна 1, так и в месте установки приемоизлучающих антенн 12.

Электронная картографическая навигационная информационная система (ЭКНИС) 10 представляет собой ЭКНИС типа «СОЭНКИ 4000-19» (Судостроение, №4, 2010, с.54) и предназначена за контролем передвижения гидрографического судна 1 при производстве батиметрической съемки и отображении информации на видео - плоттере, аналогом является панорамный эхолот-видео - плоттер типа ПЭВ-К (В.А.Воронин, С.П.Тарасов, В.И.Тимошенко. Гидроакустические параметрические системы. Ростов-на-Дону. «Ростиздат». 2004, с.302-307).

Функциональный блок 9 представляет собой аппаратно-программный блок и состоит из процессора, графических ускорителей, объектно-графического движка типа OGRE, программных модулей типа PhysX, Hydrax, Skyx и ANSYS AQWA. В качестве графического движка возможно также применение коммерческих движков типа CRY ENGINE, VALVE или аналогичных.

Предлагаемый способ стереосъемки рельефа дна акватории осуществляется следующим образом.

При движении гидрографического судна 1, оснащенного соответствующей измерительной аппаратурой (фиг.1, 2) для обеспечения задач навигации и батиметрической съемки, по запланированному съемочному галсу 20, по управляющим электрическим сигналам, выработанным в электромеханических регистраторах 14, приемопередатчиками 13 и приемоизлучающими антеннами 12 осуществляется излучение на разной частоте ультразвуковых зондирующих сигналов к поверхности дна 19 акватории съемки и приема отраженных от нее данных импульсов по направлениям, образующим с вертикальной плоскостью, перпендикулярной с диаметральной плоскостью гидрографического судна 1, два симметричных заданных угла α и регистрации отраженных от поверхности дна сигналов на самописцах механических регистраторов 14.

Продольный параллакс Р произвольных точек A и С на эхограммах электромеханических регистраторов 14 определяют в соответствии с зависимостью:

P A = X A − X A ' P C = X C − X C ' } ,                       ( 2 )

где X_A, X_C, и X A ' , X C ' - абсциссы точек А и С, снятые с эхограммы электромеханических регистраторов 14 соответственно фотограмметрическим прибором 15. Разность параллаксов может быть вычислена по формуле

Δ P = ( X A − X A ' ) − ( X C − X C ' ) ,                         ( 3 )

или по формуле Δ P = 2 M t g α h ,                       ( 4 )

где М - масштаб регистрации;

h - относительное превышение точек А и С,

h = ( X A - X A ' ) − ( X C − X C ' ) 2 M t g α .                       ( 5 )

По формулам (3), (4), (5) в блоке 16 определения параллактического смещения между соответствующими записями изображений рельефа дна на самописцах электромеханических регистраторов 14 строится стереокарта рельефа дна акватории.

При обнаружении опасных форм рельефа выполняют дополнительные галсы.

Далее по полученным дискретным измерениям строят цифровую карту рельефа дна, выполняют топологический анализ рельефа, при этом формируют граф Кронрода-Риба и комплексы Морса-Смейла для каждой кусочно-линейной поверхности, выполняют оценку фрактальных параметров рельефа посредством функционального блока 9, в котором реализован математический аппарат - топологии, в части элементов теории дифференциальной и алгебраической (комбинаторной) топологии. Применение этого аппарата позволяет единообразно математически описывать все формы рельефа независимо от масштабов и конкретных форм для отображения на карте или дисплее.

Алгебраическая топология обеспечивает связь между геометрией и алгеброй, между непрерывным и дискретным описанием рельефа, описанием структурных особенностей рельефа: точек минимумов, максимумов, линий сети тальвегов и водоразделов. Дифференциальная топология обеспечивает основу для выявления и согласования глобальных свойств поверхности рельефа с набором его локальных структурных особенностей. Все это позволяет осуществить реализацию конструктивных алгоритмов для ЭВМ.

Кроме того, аппарат дифференциальной и алгебраической топологии дает возможность приближенно восстановить поверхность по набору точечных данных, сравнивать степень близости двух представлений поверхности рельефа фиксированной области как для одного масштаба, так и для различных масштабов. Получить логически аргументированный способ упрощения рельефа как для целей генерализации, так и для удаления шума измерений.

Алгебраическая топология предоставляет набор инструментов, которые позволяют улавливать и описывать форму поверхности, определять, в чем поверхности совпадают или отличаются. Кроме того, в алгебраической топологии существуют классические инструменты, такие как теория Морса, гомотопий и гомологии, которые подходят для решения ряда вопросов, связанных с формой поверхности (Милнор Дж. Теория Морса. - М.: Издательство ЛКИ, 2011. - 184 с.).

Теория Морса устанавливает основы для описания множества критических точек гладкой функции, заданной на многообразии. Используя теорию Морса, можно определить способ описания формы поверхности, основанный на эволюции поверхности изолиний уровней, отображающей функцию. Этот способ, заключающийся в сопоставлении уровней критических точек на поверхности, как правило, рассматривается как один из самых простых способов описания геометрии поверхности. С каждой функцией оказывается связанным некоторый одномерный континуум, ее одномерное дерево. Изучение ряда свойств самой функции сводится к изучению свойств соответствующей функции на одномерном дереве. Разделение свойств функции двух переменных на «одномерные» и «двумерные» представляется факт принципиальный. С этой точки зрения введение одномерного дерева как раз существенно: с его помощью особенно четко выделяются одномерные свойства двумерной функции.

Обозначив через f^-1(r) полный прообраз значения r скалярной функции f заданной на поверхности S² (f:S²→R), а через а регулярные значения функции, т.е. такие значения, в прообразе которых нет ни одной критической точки, то в этом случае f^-1(a) всегда является гладким подмногообразием в S² в силу известной теоремы о неявной функции. Обозначим через с критические значения функции, т.е. такие значения, в прообразе которых есть хотя бы одна критическая точка. Пусть f - функция Морса на компактном гладком многообразии S². Рассмотрим произвольную поверхность уровня f^-1(a) и ее компоненты связности, которые назовем слоями. В результате многообразие разбивается в объединение слоев, получается слоение с особенностями. Подчеркнем, что каждый слой связан по определению. Объявляя каждый слой одной точкой и вводя естественную фактор-топологию в пространстве слоев Г, получаем некоторое фактор-пространство. Его можно рассматривать как базу этого слоения. Для функции Морса пространство Г является графом. Граф Г называется графом Кронрода-Риба.

Одномерные свойства функции двух переменных описываются с помощью графа Кронрода-Риба, а свойства более высокой размерности с помощью комплексов Морса-Смейла (Sharko V.V. About Kronrod-Reeb Graph of a Function on a Manifold // Methods of Functional Analysis and Topology, Vol.12 (2006), no. 4, pp.389-396. Понтрягин Л.С. Основы комбинаторной топологии. - М.; Наука, 1976. - 136 с.) для функции Морса f на многообразии S². Вершиной графа Кронрода-Риба назовем точку, отвечающую особому слою функции f, т.е. связной компоненте уровня, содержащей критическую точку функции. Вершину графа Кронрода-Риба назовем концевой, если она является концом ровно одного ребра графа. Все остальные вершины назовем внутренними. Концевые вершины графа Кронрода-Риба взаимно-однозначно отвечают локальным минимумам и максимумам функции. Внутренние вершины графа Кронрода-Риба взаимнооднозначно отвечают особым слоям функции, содержащим седловые критические точки.

Если заранее известно, что изучаемая поверхность является ориентируемой или неориентируемой, то граф Кронрода-Риба произвольной простой функции на ней позволяет восстановить топологию поверхности. Графы Кронрода-Риба рассматриваются с точностью до изоморфизма ориентированных графов. Две функции Морса на ориентируемой поверхности послойно эквивалентны тогда и только тогда, когда их графы Кронрода-Риба изоморфны.

Обобщенный механизм построения графа Кронрода-Риба сводится к следующему. Пусть на многообразии задана функция Морса. Две критические точки соединяются ребром на графе Кронрода-Риба тогда и только тогда, когда существует монотонный гладкий путь на многообразии, который соединяет эти точки и не пересекает критических слоев (кроме своих концов). Под монотонным путем понимается путь, вдоль которого данная функция возрастает. Два седла соединяются двумя ребрами на графе Кронрода-Риба тогда и только тогда, когда существуют два монотонных гладких пути на многообразии, которые соединяют эти седла и не пересекают критических слоев (кроме своих концов), причем эти пути невозможно соединить постоянным путем на многообразии (то есть внутренние точки путей принадлежат разным слоям).

Таким образом, одномерное дерево функции Морса состоит из множества концевых точек плюс не более чем счетное число простых дуг, попарно пересекающихся не более чем в одной точке, являющейся притом точкой ветвления. Следует отметить, что для вырожденной функции Морса (наличие вырожденной критической точки) сколь угодно малым шевелением функции Морса можно добиться, чтобы на каждом критическом уровне с (т.е. на множестве точек p, для которых f(p)=с) лежала ровно одна критическая точка. Другими словами, критические точки, попавшие на один уровень, можно развести на близкие уровни. Функции Морса, имеющие ровно по одной критической точке на каждом критическом уровне, называются простыми.

Для невырожденной функции Морса граф Кронрода-Риба является деревом, имеющим Т тройных точек ветвления, K=Т+2 концевых точек и Р=2Т+1 ребро, соединяющие K+Т=2Т+2 вершины графа.

Для функции Морса, топология множества уровней связана с критическими точками и полем градиента функции. Эта связь обеспечивает возможность для формального описания поверхности в алгебраической форме. В отличие от других методов топологии, основанных, например, на деревьях Кронрода-Риба, использование комплекса Морса-Смейла обеспечивает описание двумерных и многомерных свойств поверхности, что позволяет получить представление локальной топологии гладких функций и произвести сегментацию поверхности на регионы с "однородным" полем градиента. Другими словами, геометрия гладкой поверхности отображается в простые геометрические образы (симплициальные комплексы), анализ которых позволяет описать структурные особенности исходной поверхности, различной размерности: нуль-, одно- и двумерные. Эти структурные особенности легко интерпретируются в геоморфологических терминах, например, нульмерным объектам соответствуют вершины (пики) и впадины (ямы), одномерным - линии сети тальвегов, водоразделов, двумерным - монотонные склоны. Этим обеспечивается связь геометрических свойств через структурные особенности с геоморфологической семантикой.

В последнее время теория Морса была распространена до кусочно-линейных функций (Gyulassy A.G. Combinatorial Construction of Morse-Smale Complexes. Dissertation Submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy. University of California. 2008.). Такое расширение на кусочно-линейные функции и дискретные сетки позволяет использовать теорию Морса для решения практических задач с реальными наборами данных.

Критические точки функции Морса - это те точки на двумерной поверхности, где функция стационарна. Чтобы в полной мере описать функцию Морса, мы должны выделить ее структурные особенности. Для этого нужно определить векторное поле, называемое градиентом.

Градиент функции Морса является векторное поле на S². Проинтегрируем это векторное поле для того, чтобы осуществить декомпозицию S² на регионы с однородными потоками. Кривая l(t) называется интегральной линией f, если ∂ ∂ s l ( t ) = d f ( l ( t ) ) для всех t∈R. Другими словами интегральная линия есть путь, для которого касательный вектор параллелен градиенту в каждой точке пути.

Интегральные линии представляют поток вдоль градиента между критическими точками. В любой точке, где градиент не равен нулю, интегральную линию, проходящую через эту точку, можно найти, проследив вперед и в обратном направлении вдоль векторного поля градиента. Следующее определение определяет верхний и нижний пределы точек интегральной линии.

Предел lim s → − ∞ l ( t ) называется источником интегральной линии l(t) и обозначается org(t).

Предел lim s → + ∞ l ( t ) называется приемником интегральной линии l(t) и обозначается dest(l).

Интегральные линии на гладких функциях обладают следующими свойствами:

1) две интегральные линии либо пересекаются, либо же совпадают;

2) интегральные линии покрывают все S²,

3) источники и приемники интегральных линий являются критическими