Способ прокатки металлической заготовки

Способ прокатки металлической заготовки

Иллюстрации

Показать все

Реферат

Изобретение относится к способам производства проката и может быть использовано при прокатке длинномерных металлических заготовок между валками, в том числе при проявлении материалом заготовки сверхпластических свойств.

При прокатке длинномерной заготовки, имеющей простую конфигурацию поперечного сечения, в длинномерный полуфабрикат изделия с более сложной конечной конфигурацией поперечного сечения, заготовка обрабатывается определенным количеством парных валков (в прокатных клетях). На каждой паре таких валков, прокатной клети, производится часть общей деформации заготовки или подкат ее поперечного сечения под последующие операции обработки (прокатки) для бездефектного получения требуемого полуфабриката изделия. Самой низкоэффективной и трудоемкой операцией в такой технологии является выбор профиля деформирующего контура инструмента (валков) на первой операции прокатки.

Использование современных способов компьютерного моделирования процесса деформирования для интерактивной оптимизации технологических параметров и назначения выбора оптимальной геометрии деформирующего инструмента должно обеспечить высокое качество получаемого изделия и снизить энергозатраты на его производство.

Известен способ объемной штамповки заготовок в состоянии сверхпластичности, опубликованный в статье - Чумаченко Е.Н., Кривонос Г.А., Макарова Л.Т., Соломатин B.C. - Определение рациональных скоростных режимов штамповки в условиях сверхпластичности. «Кузнечно-Штамповочное Производство», Машиностроение, 1987 г, №3, с 16-17.

В соответствии с известным способом объемной штамповки заготовок в состоянии сверхпластичности на основе анализа напряженно-деформированного состояния заготовки и энергосиловых параметров процесса ее деформирования при компьютерном моделировании вводят критериальную функциональную зависимость между функциями изменения скорости деформирования, скорости и степени деформации металла в очаге деформации, структурным параметром и степенью изменения усилия деформирования. Все критерии связаны между собой функционально математическими выражениями, позволяющими, применяя пошаговые итерации, осуществить компьютерное моделирование, позволяющее определить те изменения скорости деформирования заготовки, которые обеспечат режим сверхпластического течения ее материала.

Недостатками данного способа являются:

- невозможность определения поля скоростей течения металла заготовки в направлении перпендикулярном основной плоскости движения деформирующего инструмента и, таким образом, невозможность определения оптимальной конфигурации деформирующего инструмента посредством компьютерного моделирования в 3-мерном пространстве очага деформации;

- применяемый в аналоге математический метод составления алгоритма моделирования не может реализоваться применительно к 3-мерному пространству очага деформации при установившейся стадии течения металла в очаге деформации.

Наиболее близким по технической сущности к заявляемому изобретению является способ прокатки металлической заготовки между валками (J.J.Park, S.I.Oh " Application of three dimensional finite elements to shape rolling processes." Опубликованной в журнале - Transaction of the ASME J. Engg. Ind. - 1990. - Vol.112. - FEBRUARY. - p.36-46 - «Применение 3-мерных конечных элементов при моделировании процессов прокатки»). В этом способе определение его технологических параметров - определение геометрии рабочей поверхности деформирующего инструмента, распределение напряжений и скоростей течения материала в очаге деформации осуществляется посредством имитационного компьютерного моделирования пластического течения металла в очаге деформации, включающего:

- выбор компьютерной программы для моделирования конфигурации деформирующего контура инструмента и его оптимизации с обработкой вводимых в нее данных;

- выбор эмпирической конфигурации деформирующего контура прокатных валков начальной прокатной клети и ввод ее в программу моделирования и оптимизации;

- выбор и ввод в программу для моделирования и оптимизации алгоритма, определяющего в объеме текущего очага деформации шаг моделирования, количество шагов в очаге деформации и параметр точности оптимизации с выделением в очаге деформации двух направлений моделирования - вдоль направления прокатки - ось Z, и перпендикулярно направлению прокатки - плоскость Х-Y;

- ввод в компьютерную программу алгоритма, определяющего на каждом шаге моделирования напряженно деформированное состояние среды в виде функционала;

- ввод в программу моделирования алгоритма построения в объеме каждого шага моделирования и в объеме всего очага деформации, на первой, начальной операции, N- мерных конечных элементов со свойствами твердого вязкопластичного материала и с их перестройкой на каждом шаге моделирования и оптимизации конфигурации рабочей поверхности прокатных валков, а также включающий моделирование и оптимизацию конфигурации рабочей поверхности прокатных валков на последующих операциях прокатки заготовки до получении готового изделия, при условии использования, в качестве начальной конфигурации прокатного валка, оптимальный контур, полученный на предыдущей операции моделирования прокатки заготовки, с возможностью изменения скорости прокатки через изменение геометрических параметров деформирующего инструмента и динамических параметров его привода.

К недостаткам данного способа процесса прокатки с оптимизацией конфигурации прокатного инструмента - валка посредством моделирования следует отнести:

- низкая эффективность применения моделирования применительно к производственным процессам по причине существенного возрастания затрат машинного и операционного времени по следующим причинам:

- большая размерность системы определяющих уравнений и, как следствие, большое количество неизвестных требует для получения результата или ввод дополнительных допущений, необходимых для достижения требуемого результата за счет снижения его точности, или существенного увеличенная времени перестройки 3-х мерных конечных элементов (ТКЭ) на каждом шаге моделирования по всему объему очага деформации и обработки задачи по каждому узлу ТКЭ;

- допущение в разделении течения материала заготовки в очаге деформации по двум независимым направлениям моделирования так, что составляющая скорости движения любой точки металла в очаге деформации не зависит от ее координаты в поперечном направлении, что потребует дополнительного времени обработки алгоритма для согласования результатов моделирования в целом по всему очагу деформации.

Следующий недостаток - это принятие при моделировании максимального значения трения в очаге деформации, что может привести к искажению результатов оптимизации профиля рабочей поверхности прокатного валка.

При прокатке в очаге деформации есть зоны контакта металла с поверхностью валков с существенным относительным проскальзыванием, т.е. с коэффициентом трения меньше 1,0. Это зона захвата валком металла заготовки и зона выхода металла заготовки из очага деформации. Третья зона, располагающаяся между указанными зонами есть так называемое нейтральное сечение, в которой отмечается эффект прилипания металла заготовки к поверхности валка за счет выравнивания линейных скоростей каждой точки рабочего профиля прокатного валка и прокатываемой заготовки. Геометрические параметры и расположение третей зоны очага деформации относительно центра вращения валков хорошо проработаны в работах по прокатке акад. А.И.Целикова, в которых показана существенность влияния геометрических параметров валка и динамики его привода на геометрию зоны нейтрального сечения и возможности управления распределением скоростей перемещения частиц металла в очаге деформации. Последние факторы, не используются в аналоге-прототипе, при моделировании оптимальной конфигурации деформирующего контура прокатного валка.

Технической задачей, на решение которой направлено заявляемое изобретение, является оптимизация технологических режимов деформирования с обеспечением высокого качества получаемого полуфабриката изделия и снижением энергозатрат на его производство посредством выбора оптимальной геометрии рабочего профиля прокатного валка каждой прокатной клети.

Поставленная техническая задача решается в способе прокатки металлической заготовки между профильными валками в последовательно стоящих прокатных клетях, включающий выбор профиля рабочей поверхности прокатных валков посредством имитационного компьютерного моделирования при установившейся стадии пластического течения металла в очаге деформации, с учетом состояния сверхпластичности, и деформирование заготовки в прокатных валках последовательно установленных прокатных клетей с изменением скорости деформирования заготовки в каждой прокатной клети за счет выбора профиля рабочей поверхности валка последующей прокатной клети на основе оптимального профиля валка предыдущей прокатной клети. При этом профиль рабочей поверхности прокатного валка выбирают с учетом распределения скоростей (V_x,V_y)_k течения металла заготовки в очаге деформации в направлениях, перпендикулярных направлению прокатки и взаимосвязанной с этими скоростями скорости (V_z)_k течения металла заготовки в направлении прокатки, которую вычисляют по математическому выражению:

, при условии Z ⌣ ∈ Δ Z k ,

где:

C_k, принимаемую за постоянную величину равную ε / z - скорости деформации в направлении прокатки для каждого элементарного объема ΔZ_k, определяют по минимому математического выражения:

∫ S σ z d x d y + 2 ( t g α ± η ) ∫ Г σ n d Г − σ z H S ≤ ξ , при условии Z∈ΔZ_k,

где:

- ξ - малое, наперед выбираемое число, стремящееся к нулю, но не равное нулю;

X, Y - координаты, перпендикулярные направлению прокатки;

Z - координата, совпадающая с направлением прокатки;

- K - номер элементарного объема ΔZ_k, на которые разбивают объем очага деформации;

- ∈ - означает принадлежность координаты Z элементарному объему ΔZ_k очага деформации;

- σ z H - напряжение натяжения металла заготовки на выходе из очага деформации, при его возникновении;

- S - текущая площадь поперечного сечения заготовки относительно элементарного объема ΔZ_k очага деформации;

- Г - боковая поверхность элементарного объема ΔZ_k очага деформации;

- 2(tgα±η) - множитель, учитывающий трение на границе металл

заготовки - инструмент, где: η - коэффициент по закону Кулона и α - угол контакта металла заготовки с инструментом для каждого элементарного объема ΔZ_k очага деформации;

- σ_n - нормальные напряжения, действующие на боковую поверхность Г элементарного объема ΔZ_k очага деформации;

- σ_z - напряжение, действующее вдоль направления прокатки - ось Z, в элементарном объеме ΔZ_k очага деформации, зависящее от конфигурации боковой поверхности элементарного объема ΔZ_k очага деформации, величины накопленного в нем гидростатического давления σ* и показателя сжимаемости материала заготовки;

- f_k - слагаемое, используемое в качестве поправки определяемой скорости (V_z)_k частиц элементарного объема ΔZ_k очага деформации относительно скорости перемещения частиц металла заготовки в нейтральном сечении очага деформации, при этом, шаг определения скоростей, для каждого элементарного объема ΔZ_k очага деформации, по каждой прокатной клети определяют из интервала:

10 < Z B Δ Z k < 300 ,

где Z_B - длина очага деформации в направлении прокатки.

Чертежи, поясняющие заявляемое изобретение:

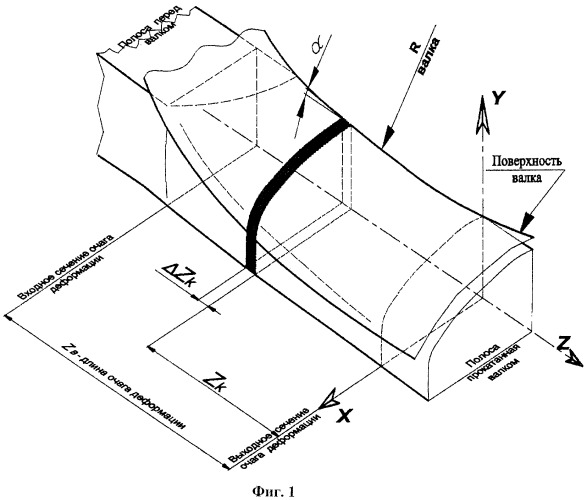
- на фиг.1 показана схема очага деформации (пространственная схема одной четверти заготовки) при продольной прокатке с частью рабочей поверхности валка;

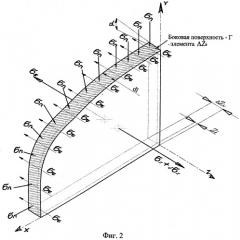
на фиг.2 показана схема распределения напряжений по поверхностям элементарного объема ΔZ_k в очаге деформации.

Способ осуществляется следующим образом.

При имитационном компьютерном моделировании объемного распределения в очаге деформации скоростей перемещения частиц металла заготовки очаг деформации программно разбивается на два взаимосвязанных и ортогональных направления:

- первое направление в плоскости Х-Y, перпендикулярное направлению прокатки - ось Z, и имеющее элементарное приращение в направлении оси Z толщиной ΔZ_k, образующее элементарный объем ΔZ_k очага деформации, характеризуемый неизменным квазистатическим течением металла заготовки, соответствующего вязко пластичной среде, и в плоскости этого направления, посредством программного кода формы, строится сетка 2-у мерных конечных элементов (ДКЭ) для компьютерного моделирования распределения скоростей V_x, V_y, определяемое алгоритмом конечно-элементной аппроксимации, и располагающееся в очаге деформации по направлению прокатки с координатой Z_k относительно центра вращения валка, спроецированного на ось Z, как начала координат, где k - номер элементарного объема очага деформации;

- второе - направление, совпадающее с направлением оси Z, направлением прокатки, по которому характеристики относительной скорости перемещения частиц металла в элементарном объеме ΔZ_k очага деформации принимаются равными постоянной величине, аналитически выраженной в виде функционала.

Полная картина распределения в объеме очага деформации относительных скоростей частиц деформируемого металла и напряжений получается после компьютерной интеграции напряженно деформированных состояний по каждому элементарному объему ΔZ_k, распределенных в длине очага деформации с заранее выбранным шагом. Полученные результаты используются в построении смоделированной конфигурации рабочего профиля прокатных валков каждой прокатной клети.

Сравнивая результаты компьютерного моделирования с требованиями бездефектного заполнения металлом рабочего профиля прокатных валков каждой прокатной клети, оценивают оптимальность смоделированного контура.

При невыполнении требований бездефектного заполнения смоделированного рабочего профиля прокатных валков каждой прокатной клети металлом заготовки, моделирование конфигурации рабочего профиля прокатных валков каждой прокатной клети переходит на повторный шаг моделирования при изменении или эмпирически выбранного контура прокатных валков, или характерного размера прокатных валков по элементу контура, или скоростного параметра привода прокатных валков, или одновременно всех перечисленных параметров.

При выполнении бездефектного заполнения металлом заготовки смоделированного рабочего профиля прокатных валков, контур принимают оптимально смоделированным для данной операции и считают исходным контуром для моделирования по такому же алгоритму последующих операций прокатки заготовки для получения требуемого полуфабриката изделия на выходе из последней клети.

Таким образом, без существенной потери точности вычислений, задавая одно из относительных перемещений металла в очаге деформации в аналитическом виде, получают малое число неизвестных параметров, уменьшающее количество разрешающих уравнений и позволяющее свести решение объемной задачи к некоторой последовательности решений обобщенных двумерных задач.

Для упрощения изложения сущности заявляемого изобретения, рассмотрим решение поставленной задачи на примере продольной прокатки металлической полосы (на основании симметрии рассматривается четверть сечения очага деформации прокатываемой полосы - фиг.1).

Задача формоизменения в очаге деформации решается в скоростях перемещения с принятием ряда допущений:

- формоизменение в очаге деформации происходит медленно -квазистатический процесс, т.е. динамическими эффектами пренебрегают и течение частиц металла в очаге деформации считают установившимся, при этом, весь временной интервал разбивают на под- интервалы Δt, внутри которых изменение скорости перемещений не происходит;

- рассматривают бесконечно малый элементарный объем очага деформации - ΔZ_k - на расстоянии Z_k от проекции на ось Z координаты центра прокатного валка;

- на основании полуаналитического метода конечных элементов (МКЭ), для элементарного объема ΔZ_k значение скорости деформации ε / z вдоль оси Z принимают равной постоянной величине, а именно:

ε Z /   | Z = Z ⌣ = C k , при условии Z∈[Z_k, Z_k+ΔZ_k],

где ∈ обозначает принадлежность переменной Z промежутку - [Z_k, Z_k+ΔZ_k].

Отсюда, в каждой точке (х, y, z) очага деформации, в любой момент времени t, должна быть найдена функция V_zk (х, у, z, t), характеризующая скорость перемещения материала в произвольно выбранной точке. При этом, в каждом конечном элементарном объеме ΔZ_k сечения очага деформации компоненты скорости перемещения частиц материала заготовки будут определяться следующими функциями:

V_x=V_x(x,y); V_y=V_y(x,y); V_z=C_kz.

Таким образом, пространственное, трехмерное поле скоростей перемещения частиц материала в очаге деформации, в том числе и в элементарном объеме - ΔZ_k сечения очага деформации разделяют на два составляющих поля:

- (V_x, V_y)_k - поле скоростей в плоскости Х-Y, перпендикулярной оси Z для каждого элементарного объема ΔZ_k очага деформации, рассчитываемое по обобщенной плоской, двумерной задаче с помощью МКЭ или конечно элементной аппроксимацией;

- (V_z)_k - поле скоростей вдоль оси Z, рассчитываемое из условия минимизации функционала, вычисляемого на основании уравнения равновесия для каждого элементарного объема ΔZ_k очага деформации в соответствующий момент времени.

Рассматривая условия баланса всех сил, действующих в направлении прокатки на элементарный объем ΔZ_k, выделенный сечениями Z_k и Z_k+dz, получают общее выражение для функционала

Ф ( C k ) = ∫ S σ Z d x d y + 2 ( t g α ± η ) ∫ Г σ n d Г − σ z H S ,

который определяется, при компьютерном моделировании, для каждого k-го элементарного объема ΔZ_k очага деформации с учетом рабочего профиля прокатного валка, полученного на k-1 шаге моделирования, принимается постоянной величиной, приравниваемой скорости деформации в виде - ε Z /   | Z = Z ⌣ = C k и содержит следующие влияющие параметры:

σ_n - нормальные напряжения, действующие на боковую поверхность элементарного объема ΔZ_k по контуру поверхности Г (фиг.1), определяемые выражением

σ n = [ 2 μ ∂ V x ∂ x + ( K ⋅ Δ t − 2 3 μ ) ( ∂ V x ∂ x + ∂ V y ∂ y ) + σ * ] ⋅ n x + μ ( ∂ V x ∂ x + ∂ V y ∂ y ) n y ,

где

μ = μ ( ε u , ε ˙ u , T ) функция, определяемая экспериментально и характеризующая физические свойства прокатываемого материала в зависимости от деформации ε_u, скорости деформации ε ˙ u и температуры Т;

K - коэффициент объемного сжатия (константа материала);

n_x и n_y - направляющие косинусы нормали к полосе в зоне контакта с валками (определяются для k-го шага по решению на k-1 шаге);

Δt - шаг решения, определяемый из (V_z)_k Δt=ΔZ_k, при этом, в зависимости от требуемой точности моделирования, величину ΔZ_k выбирают из соотношения - 10 < Z B Δ Z k < 300 или с учетом рекомендации - Z B Δ Z k = 100 , в которых Z_B - геометрический размер очага деформации в направлении прокатки;

σ* - накопленное гидростатическое напряжение в элементарном объеме ΔZ_k очага деформации, определяемое из выражения - σ * = K [ − θ ˙ ⋅ Δ t + ∫ 0 t θ ˙ d t ] = K ∑ i = 0 k − 1 Δ t i θ ˙ i , в которой θ ˙ = ∂ V x ∂ x + ∂ V y ∂ y + ∂ V z ∂ z ;

σ_z - напряжение, действующее вдоль оси Z, перпендикулярно к поверхности - S элементарного объема ΔZ_k - зависит от рабочего профиля прокатного валка в зоне элементарного объема ΔZ_k и величины накопленного гидростатического давления σ* в том же ΔZ_k очага деформации, определяемое соотношением:

σ z = ( K ⋅ Δ t − 2 3 μ ) ( ∂ V x ∂ x + ∂ V y ∂ y ) + σ * ;

σ z H - возможный натяг полосы за счет рассогласования скоростей соседних валков при проходе полосы в системе калибров;

2(tgα±η) - множитель, учитывающий трение η по закону Кулона на границе металл заготовки - инструмент и угол α контакта металла заготовки с валком для каждого элементарного объема ΔZ_k очага деформации.

При этом, применение знака ±, применительно к продольной прокатке, обусловлено учетом возникающих сжимающих напряжений вдоль оси Z вблизи входного сечения очага деформации и растягивающих напряжений вблизи выходного сечения очага относительно нейтрального сечения в нем.

Минимум же модуля функционала, обозначенного выше и позволяющего найти значения (V_z)_k для каждого элементарного объема ΔZ_k очага деформации, определяется в виде

|Ф(C_k)|≤ξ,

где

ξ - малое, наперед заданное число, стремящееся к нулю, но не равное нулю, и позволяющее обеспечить необходимую точность решения при определении C_k в процессе компьютерного моделирования при оптимизации, например, эмпирически выбранного деформирующего контура прокатного валка (инструмента).

Поле скоростей (V_x,V_y)_k определяют, с учетом начальных и граничных условий, решением ниже представленных дифференциальных уравнений:

{ σ i j , j = 0 σ i j = μ ( ∂ V x ∂ x + ∂ V y ∂ y ) + [ ( K ⋅ Δ t − 2 3 μ ) u p , p + σ * ] δ i j ,

где

δ_ij - символ Кронекера.

Координата размещения Z* нейтрального сечения, применительно к прокатке, по длине очага деформации зависит от геометрии деформирующего контура инструмента, от угла контактирования прокатного валка с прокатываемым материалом для каждого элементарного объема ΔZ_k, скорости вращения прокатных валков и определяется из выражения

Z * = R 2 ( Z B R − 1 − R + h − H R η ) ,

где

R - радиус валка;

Н, h - соответственно высота полосы проката на входе и на выходе из валков;

После того как получено решение функционала во всех k-х элементарных объемах ΔZ_k очага деформации, переходят к определению скоростей перемещения материала заготовки по всему очагу деформации в направлении прокатки (V_z)_k.

Значения скоростей (V_z)_k вычисляют для каждого элементарного объема ΔZ_k из соотношения

( V z ) k = C k ⋅ Z ⌣ + f k ( z ) , при условии Z ⌣ ∈ Δ Z k ,

где: f_k(z) - скорость перемещения элементарного объема ΔZ_k в очаге деформации, определяемая по:

f k ( z ) = f 0 + ∑ n = 1 k − 1 C n ⋅ Z n ,

где:

k - номер сечения очага деформации;

f₀ - скорость входа полосы в валки прокатного стана, определяемая по скорости нейтрального сечения в очаге деформации - Z*, угловой скорости валков Ω и их радиуса R по выражению

f m ( z * ) = f 0 + ∑ n = 1 m C n ⋅ Z * = Ω ⋅ R ⋅ sin β ,

где m - номер элементарного объема сечения, в котором расположено нейтральное сечение с координатой Z*;

β = arcsin Z * R - угол, определяющий нейтральное сечение в очаге деформации при прокатке (соответствует положению Z* относительно центра валка).

Таким образом, производят определение распределения скоростей по всему объему очага деформации заготовки относительно текущей операции. При этом, применительно к продольной прокатке, для текущего решения относительно текущей клети, начальной конфигурацией деформирующего контура инструмента является профиль деформирующего контура инструмента, полученный в предыдущей клети прокатного стана.

При осуществлении компьютерного моделирования и оптимизации конфигурации рабочего профиля прокатных валков на последующих операциях деформирования заготовки в качестве начальной конфигурации деформирующего контура инструмента используют оптимальный контур, полученный на предыдущей операции моделирования прокатки заготовки, с возможностью изменения скорости прокатки через изменение геометрических параметров прокатных валков и динамических параметров их привода.

Пример эффективности применения заявляемого способа при компьютерном моделировании оптимальной конфигурации калибра деформирующего инструмента - прокатных валков прокатного стана в сопоставлении со способом компьютерного проектирования конфигурации такого же инструмента на основе 3-х мерных конечных элементов (ТКЭ).

В прототипе представлялась трехмерная модель компьютерного моделирования прокатки в калибрах с применением трехмерных конечных элементов и использованием программы SHPROL. С помощью ТКЭ в указанной программе задавали конфигурацию профиля валка и, в процессе компьютерного моделирования процесса прокатки полосы, прослеживали постепенность ее деформации в требуемый профиль. Моделирование производилось с выполнением условий изотермического деформирования.

По заявляемому изобретению были поставлены аналогичные численные эксперименты (компьютерное моделирование) по прокатке в калибрах с использованием программного пакета SPLEN (Caliber), в котором применяли МКЭ метод с двумерными конечными элементами. Численные эксперименты поводили с таким же изделием, что и авторы статьи - прототипа - полоса прямоугольного сечения 50,8× 50,8 мм.

Сравнительный численный анализ был проведен как в гладких, так и в профильных валках. Материал полосы - Ст.45 - аналог стали AISI- 1045, которая использовалась в статье - прототипа. Температура нагрева для моделирования принималась 1100°С и температурные условия деформирования изотермические.

В расчетах с помощью SHPROL, выполненными, в силу осевой симметрии сечения полосы, на четверти ее сечения, использовано разбиение модели на 640 пространственных, трехмерных элементов с 1025 узлами. При этом, вычисления проводились на компьютере VAX-11/750, для получения решения потребовалось 2600 итераций, что заняло порядка 175 часов вычислений.

Численные эксперименты по моделированию конфигурации валков при прокатке с помощью SPLEN (Caliber) с использованием заявляемого способа. Было выбрано сто сечений очага деформации (k=1÷100) по 352 конечных элемента в каждом сечении. Время расчета на Pentium 4 заняло порядка 100 мин. Ошибки вычислений не превышали 6…8%.

Для получения распределения нормальных напряжений на прокатываемой полосе в расчетах авторов [2] потребовалось: 1000 ТКЭ с 1476 узлами и 3200 итераций, что вылилось в 470 часов работы компьютера VAX-11/750 (достаточно мощная вычислительная техника).

Получение аналогичной информации, при численных экспериментах по заявляемому способу, с использованием программы SPLEN (Caliber) на компьютере Pentium 4 потребовалось не более 5 мин. Приведенное в примерах компьютерное оборудование по основным системным требованиям имело почти одинаковые показатели.

Заявляемый способ прокатки металлической заготовки между валками позволяет оптимизировать технологические режимы прокатки с обеспечением высокого качества получаемого полуфабриката изделия и снизить энергозатраты на его производство посредством выбора, с использованием компьютерного моделирования, оптимальной геометрии рабочей поверхности прокатных валков каждой прокатной клети.

Способ прокатки металлической заготовки между профильными валками в последовательно стоящих прокатных клетях, включающий выбор профиля рабочей поверхности прокатных валков посредством имитационного компьютерного моделирования при установившейся стадии пластического течения металла в очаге деформации с учетом состояния сверхпластичности и деформирование заготовки в прокатных валках последовательно установленных прокатных клетей с изменением скорости деформирования заготовки в каждой прокатной клети за счет выбора профиля рабочей поверхности валка последующей прокатной клети на основе оптимального профиля предыдущей прокатной клети, отличающийся тем, что профиль рабочей поверхности прокатного валка выбирают с учетом распределения скоростей (V_x,V_y)_k течения металла заготовки в очаге деформации в направлениях, перпендикулярных направлению прокатки, и взаимосвязанной с этими скоростями скорости (V_z)_k течения металла заготовки в направлении прокатки, которую вычисляют по математическому выражению: , при условии Z ⌣ ∈ Δ Z k ,где C_k - постоянная, равная скорости деформации в направлении прокатки для каждого элементарного объема ΔZ_k очага деформации, определяемая по минимуму математического выражения: ∫ S σ z d x d y + 2 ( t g α ± η ) ∫ Г σ n d Г − σ z H S ≤ ξ , при условии Z∈ΔZ_k,ξ - малое, наперед выбираемое число, стремящееся к нулю, но не равное нулю;X, Y, - координаты, перпендикулярные направлению прокатки;Z - координата, совпадающая с направлением прокатки;k - номер элементарного объема (ΔZ_k), на которые разбивают объем очага деформации;∈ - принадлежность координаты Z элементарному объему ΔZ_k очага деформации; σ z H - напряжение натяжения металла заготовки на выходе из очага деформации при его возникновении, МПа;S - текущая площадь поперечного сечения заготовки относительно элементарного объема очага деформации ΔZ_k, мм²;Г - боковая поверхность элементарного объема очага деформации ΔZ_k, мм