Способ определения модуля упругости материала покрытия на изделии

Способ определения модуля упругости материала покрытия на изделии

Иллюстрации

Показать все

Реферат

Изобретение относится к измерительной технике для определения модуля упругости материала тонких покрытий на изделии.

Известен способ определения модуля упругости материала покрытий на изделии, заключающийся в том, что в поверхность с покрытием с известной толщиной внедряют сферический индентор с известными упругими характеристиками и радиусом, записывают диаграмму изменения нагрузки от глубины внедрения и для участка диаграммы, отвечающей упругому деформированию материала покрытия, рассчитывают модуль упругости материала покрытия Е_пок из аналитического соотношения, связывающего обобщенный приведенный модуль упругости образца с покрытием E** с толщиной покрытия, геометрией контакта, упругими свойствами материала основы и покрытия, а также эмпирическим параметром α:

Е о б * = Е п о к * 1 − ( λ + k + 4 k α 2 ) θ + λ k θ 2 1 + α k θ − λ k θ 2 ; k = τ − 1 τ + ( 3 − 4 μ п о к ) ; λ = 1 − 4 ( 1 − μ п о к ) 1 + τ ( 3 − 4 μ п о к ) ; 1 Е * * = 1 Е о б * + 1 Е и * ; a 0 = 3 P R 4 E 0 * 3 ; 1 Е о * = 1 Е и * + 1 Е о с * ; T c = h a 0 ; θ=ехр(-2α), E * * = 3 P 4 R s 3 ; α=f(T_c),

где τ = E п о к ( 1 + μ о б ) Е о с ( 1 + μ п о к ) - модуль сдвига, s - глубина внедрения индентора в слоистое тело, h - толщина покрытия, Е*=E/(1-µ²); Е*, Е, µ - приведенные модули упругости, модули нормальной упругости и коэффициенты Пуассона образца с покрытием, индентора, подложки и покрытия, соответственно; «об», «и», «ос», «пок» - подстрочные индексы, обозначающие, что параметр, у которого они стоят, относится к образцу с покрытием, индентору, материалу основы или материалу покрытия, соответственно, α - экспериментально определяемая функция, учитывающая отличие характера распределения давления от Герцевского с изменением относительной толщины покрытия ( h a 0 ) (Патент US 7165463 В2, 23.01.2007).

Недостатком этого способа является низкая точность определения величины модуля упругости материала тонкого покрытия, связанные с трудностью точного определения области диаграммы нагружение - внедрение, отвечающей упругому деформированию только материала покрытия, а также низкой точностью определения функции α, учитывающей отличие характера распределения давления от Герцевского с изменением относительной толщины покрытия.

Известен способ определения модуля упругости материала покрытия на изделии, включающий измерение толщины покрытия, твердости и модуля упругости материала основы изделия, установку изделия в микротвердомер, с помощью которого производят внедрение алмазного пирамидального индентора Виккерса в изделие, на глубину, превышающую толщину покрытия, запись диаграммы изменения величины нагрузки с изменением глубины внедрения индентора (J. Mencik D. Munz Е. Quant E.R. Weppelmannand M.V. Swain. Determination of elastic modulus of thin layers using nanoindantation. J. Mater. Res., Vol. 12, No. 9, 1997, pp.2475-2484).

Данный способ по технической сущности и достигаемому результату наиболее близок к предложенному техническому решению, и поэтому, принят за его ближайший аналог.

Согласно этому способу в поверхность с покрытием внедряют алмазный пирамидальный индентор с известными упругими характеристиками, записывают диаграмму изменения нагрузки при нагружении и разгружении от глубины внедрения и для начального участка разгружения определяют обобщенный модуль упругости Ε**системы «слоистое тело + индентор» по формуле

E * * = π 2 ⋅ d P d s ⋅ 1 A

который потом используют для определения значения приведенного модуля упругости E о б * слоистой системы (образца с покрытием) из уравнения

1 Е * * = 1 Е о б * + 1 Е и *

которое, в свою очередь, используют для определения модуля нормальной упругости Е_пок материала тонкого покрытия из уравнения

E о б * = Е о с * + ( Е п о к * − Е о с * ) ⋅ ψ ( s c h )

где А - площадь проекции отпечатка индентора в образце под нагрузкой, d P d s - наклон кривой разгружения в начале снятия нагрузки при записи диаграммы «нагружение/разгружение - глубина внедрения», s - глубина внедрения индентора в слоистое тело, s_c - контактная (пластическая) глубина внедрения, h - толщина покрытия, Е*=E/(1-µ²); Е*, Е, µ - приведенные модули упругости, модули нормальной упругости и коэффициенты Пуассона образца с покрытием, индентора, подложки и покрытия, соответственно;«об», «и», «ос», «пок» - подстрочные индексы, обозначающие, что параметр, у которого они стоят, относится к образцу с покрытием, индентору, материалу основы или материалу покрытия, соответственно, ψ ( s c h ) - экспериментально определяемая весовая функция относительного внедрения ( s c h ) .

Недостатком этого способа является сложность определения величины модуля упругости материала тонкого покрытия, связанная с эмпирическим характером определения весовой функции относительного внедрения ψ ( s c h ) для слоистых тел.

Задача, решаемая в предлагаемом способе, упрощение способа определения величины модуля упругости материала тонкого покрытия.

Решение поставленной задачи достигается за счет того, что предложен способ определения модуля упругости материала покрытия на изделии, включающий измерение толщины покрытия, твердости и модуля упругости материала основы изделия, установку изделия в микротвердомер, с помощью которого производят внедрение алмазного пирамидального индентора Виккерса в изделие на глубину, превышающую толщину покрытия, запись диаграммы изменения величины нагрузки с увеличением глубины внедрения индентора, поле чего по диаграмме «нагрузка - внедрение» строят зависимость изменения относительной композиционной микротвердости ( H c H o ) от относительной толщины покрытия h a c , аппроксимируют возрастающую ветвь кривой изменения относительной композиционной твердости и определяют модуль нормальной упругости материала покрытия E₁, по результатам численного решения уравнения:

( Φ { h ¯ * } ) ( 1 2 ) = T k * { h ¯ * } 0,31

где T k { h ¯ * } = 1 2 ⋅ [ 3 2 ⋅ ( 1 + ( h ¯ * ) 2 ) − 1 − 1,3 ⋅ ( 1 − h ¯ * ⋅ a r c t g ( 1 h ¯ * ) ) ]

h ¯ * = h a c * , a c * h = 2,5 ⋅ s * h

( Φ { h ¯ * } ) = ∑ i = 0 m A i ( h ¯ * ) i ∑ j = 0 n B j ( h ¯ * ) j , A i = f ( K ; h ¯ * ) , B j = f ( K ; h ¯ * ) ,

K = E 0 E 1 + K u

K u = 1 − μ u 2 E u

E₁, E₀ - модули нормальной упругости материалов покрытия и основы (подложки), E_u, µ_u - модуль нормальной упругости и коэффициент Пуассона материала индентора, А₁, А₂, А₃, … A_i, В₁, В₂, В₃, … B_j - коэффициенты двухточечной Паде-аппроксиманты, h - толщина покрытия, h ¯ * - результат численного решения системы уравнений:

H c I I { t ¯ 0 } H 0 = 0,31 ⋅ T k − 1 { t ¯ 0 }

b + a ⋅ h ¯ = 0,31 T k { h ¯ }

где t ¯ 0 = t 0 a 0 , h ¯ = h a c , а_с=2,5·s,

b, а - коэффициенты аппроксимирующей функции возрастающей ветви кривой изменения относительной композиционной твердости ( H c H o ) от относительной толщины покрытия h ¯ = h a c , s - текущая глубина внедрения, экспериментально определяемая в течение всего времени испытания на приборе твердометре, а₀, a_c - предельные радиусы пятна контакта для материала основы и слоистого тела с покрытием толщиной h при внедрении в них сферического индентора радиуса R с силой Р.

Сущность предлагаемого способа заключается в том, что сопоставляют между собой значения твердости, рассчитываемой из результатов экспериментов по внедрению пирамидального индентора в слоистое тело с известными значениями твердости и модуля Юнга материала основания, а также толщины покрытия, со значениями теоретической твердости этого же слоистого тела, рассчитываемыми по известным зависимостям (Воронин Н.А. Теоретическая оценка композиционной и истинной твердости тонких покрытий. Трение и смазка в машинах и механизмах. 2011, №7, с.11-21) при одинаковых значениях глубины внедрения индентора и вычисляют величину модуля Юнга материала покрытия. Способ заключается в том, что определяют толщину покрытия и твердость материала основы известными методами, производят нагружение (внедрение) алмазного пирамидального наконечника в исследуемую плоскую поверхность, имеющую покрытие известной толщины на глубину, превышающую 1/10 долю толщины покрытия, записывают диаграмму изменения величины нагрузки с увеличением глубины внедрения, по которой строят зависимость изменения относительной поверхностной микротвердости ( H c H o ) (относительной композиционной микротвердости) от обратной величины относительной глубины внедрения ( h s ) , аппроксимируют возрастающую ветвь кривой изменения относительной композиционной твердости в виде математической зависимости и определяют модуль нормальной упругости материала покрытия по результатам численного решения уравнения:

Φ ( 1 2 ) = T k * { h ¯ * } 0,31

где T k { h ¯ * } = 1 2 ⋅ [ 3 2 ⋅ ( 1 + ( h ¯ * ) 2 ) − 1 − 1,3 ⋅ ( 1 − h ¯ * ⋅ a r c t g ( 1 h ¯ * ) ) ] , h ¯ * = h a c * , a c * h = 2,5 ⋅ s * h ,

Φ = ∑ i = 0 m A i ( h ¯ * ; K ) i ∑ j = 0 n B j ( h ¯ * ; K ) j , A i = φ ( K ; h ¯ * ) , B j = φ ( K ; h ¯ * ) , K = E 0 E 1 − K u , K u = 1 − μ u 2 E u ,

Е₁, Е₀ - модули нормальной упругости материалов покрытия и основы (подложки), E_u, µ_u - модуль нормальной упругости и коэффициент Пуассона материала индентора, h - толщина покрытия, h ¯ * - результат численного решения системы уравнений:

H c I I { t ¯ 0 } H 0 = 0,31 ⋅ T k − 1 { t ¯ 0 }

b + a ⋅ h ¯ = 0,31 T k { h ¯ }

где b, а - коэффициенты аппроксимирующей функции возрастающей ветви кривой изменения относительной композиционной твердости ( H c H o ) от обратной величины относительной глубины внедрения ( h s ) , s - текущая глубина внедрения, экспериментально определяемая в течение всего времени испытания, H_c - текущее значение композиционной твердости поверхности с покрытием, рассчитываемое для соответствующего значения s, а_с предельный радиус отпечатка, соответствующий переходу от упругой деформации к чисто пластической при внедрении в поверхность упругого жесткопластичного двухслойного полупространства жесткой сферы, Н₀ - значение микротвердости материала основы (подложки), А₁, А₂, А₃, … A_i, В₁, В₂, В₃, … Bj - коэффициенты двухточечной Паде-аппроксиманты, рассчитываемые по известным формулам (Н.А. Воронин. Расчет параметров упругого контакта и эффективных характеристик топокомпозита для случая взаимодействия последнего со сферическим индентором. Трение и износ. 2002, т.23, №6, с.583-596).

Отличительным признаком изобретения является то, что определение модуля нормальной упругости материала покрытия производят по результатам исследования отклика слоистого тела на внедрение индентора в области упругопластического деформирования слоистого тела, а не по результатам отклика на упругое деформирование слоистого тела после создания пластического отпечатка в слоистом теле. Таким образом, предлагаемый способ позволяет существенно упростить процедуру определения нормального модуля упругости тонкого покрытия за счет меньшего числа экспериментов и повысить точность определения упругой характеристики материала покрытия, так как в заявляемом техническом решении осуществляется измерение усредненного модуля Юнга по толщине покрытия в данной точке материала покрытия за одно испытание, в то время как в прототипе осреднение параметра происходит по результатам нескольких испытаний, да еще проводимых в разных точках исследуемой поверхности, физико-механические характеристики которых (точек исследования) может существенно отличаться.

Проведенный заявителем анализ техники, включающий поиск по патентным и научно-техническим источникам информации и выявление источников, содержащих сведения об аналогах заявленного изобретения, позволил установить, что заявителем не обнаружен аналог, характеризующийся признаками, идентичными всем существенным признакам заявленного изобретения, а определение из перечня выявленных аналогов прототипа, как наиболее близкого по совокупности признаков аналога, позволил выявить совокупность существенных (по отношению к усматриваемому заявителем техническому результату) отличительных признаков в заявленном объекте, изложенных в формуле изобретения. Следовательно, заявленное изобретение соответствует требованию "новизна" по действующему законодательству.

Для проверки соответствия заявленного изобретения требованию изобретательского уровня заявитель провел дополнительный поиск известных решений, с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного изобретения, результаты которого показывает, что заявленное изобретение не следует для специалиста явным образом из известного уровня техники, поскольку из уровня техники, определенного заявителем, не выявлено влияние предусматриваемых существенными признаками заявленного изобретения действий на достижение технического результата. Следовательно, заявленное изобретение соответствует требованию "изобретательский уровень" по действующему законодательству.

Предлагаемый способ поясняется чертежами, представленными на фиг.1-5.

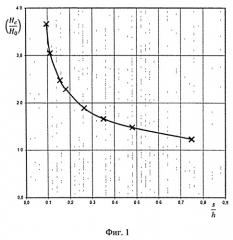
На фиг.1 изображена зависимость относительной композиционной микротвердости ( H c H o ) твердой поверхности с тонким покрытием от относительной величины глубины внедрения ( s h ) , полученная из экспериментального исследования. Маркеры обозначают экспериментальные точки.

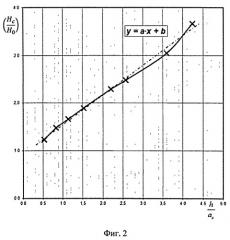
На фиг.2 изображена зависимость относительной композиционной микротвердости ( H c H o ) твердой поверхности с тонким покрытием от относительной толщины покрытия ( h a c ) полученная из зависимости, представленной на фиг.1, путем преобразования значений относительной величины глубины внедрения ( s h ) в значения относительной толщины покрытия ( h a c ) . Здесь же приведена линейная аппроксимация приведенной зависимости.

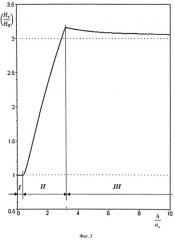
На фиг.3 изображена зависимость теоретической относительной микротвердости ( H c H o ) слоистого тела с характеристиками К=0,5 и Y=3 от относительной толщины покрытия ( h a c ) .

На фиг.4 изображены зависимости теоретической относительной композиционной микротвердости ( H c H o ) , относящиеся к участку II (см. фиг.3), от относительной толщины покрытия модельного слоистого тела ( t 0 a 0 ) (1) и реального топокомпозита ( h a c ) (2) с характеристиками К=0,5 и Y=3.

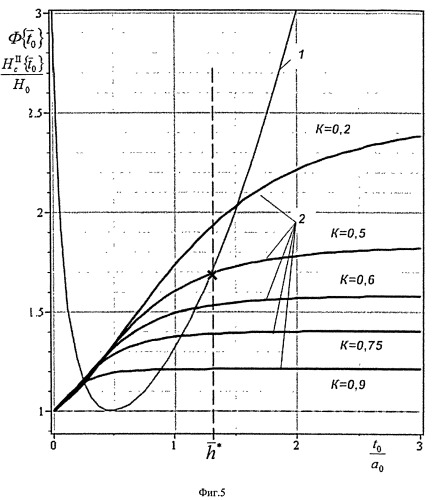
На фиг.5 изображены зависимости упругогеометрического параметра Φ { t ⇀ 0 } (l) для ряда значений параметрами относительной твердости H c I I { t ¯ 0 } H 0 (2) для модельного слоистого тела и искомая точка их взаимного пересечения при значении t ¯ 0 = h ¯ * .

Способ определения модуля нормальной упругости тонких покрытий реализуется следующим образом.

Для исследуемой твердой поверхности с тонким покрытием (слоистой системы) измеряют толщину покрытия h, модуль нормальной упругости Е₀ и микротвердость Н₀ материала основы (подложки) известными методами. В случае использования стандартного материала в качестве подложки записывают значения модуля нормальной упругости Е₀ и значение микротвердости из справочников. Записывают известные значения упругих характеристик алмазного индентора: модуля Юнга E_u и коэффициента Пуассона µ_u. С помощью прибора - твердометра с непрерывной регистрацией нагрузки и глубины погружения индентора - внедряют алмазный наконечник в виде четырехугольной пирамиды в исследуемую слоистую систему (поверхность с тонким покрытием) и производят запись диаграммы «нагрузка Р - внедрение s». Внедрение в исследуемую поверхность производят на глубину, не меньшую, чем толщина покрытия, и всегда большую, чем 1/10 доля толщины покрытия. По полученной диаграмме «нагрузка - внедрение» рассчитывают микротвердость Н_с поверхности с покрытием, по известной методике, как для однородного твердого тела (Методы определения твердости металлических материалов: Учебно-справочное пособие. / А.Г. Калмыков, Ю.И. Головин, В.Ф. Терентъев и др.; Воронеж: Изд-во ВГТУ, 2000, 80 с., стр.37). Так как исследуемая поверхность представляет собой слоистой твердое тело, то полученная зависимость микротвердости от глубины внедрения s изменяется (уменьшается с увеличением глубины внедрения). Традиционно считается (Puchi-Caberra E.S, Berrios L.A, Teer D.G. On the computation of the absolute hardness of thin solid films. Surfaceand Coatings Technology, v. 157, N 2-3, 2002, pp.185-196), что зависимость микротвердости от глубины внедрения для слоистых тел (упрочненных поверхностей, поверхностей с покрытием, топокомпозитов) при глубинах внедрения индентора более чем 1/10 доля толщины покрытия, представляет собой зависимость композиционной микротвердости от глубины внедрения. Зная величину микротвердости материала основы и толщину покрытия на исследуемой поверхности, перестраиваем зависимость композиционной микротвердости от глубины внедрения в зависимость относительной композиционной микротвердости от относительной глубины внедрения (фиг.1). Под относительной композиционной микротвердостью понимается отношение композиционной микротвердости исследуемой слоистой поверхности к микротвердости материала основы подложки ( H c H o ) . Под величиной относительной глубины внедрения понимается отношение глубины внедрения к толщине покрытия ( h s ) . Затем зависимость относительной композиционной микротвердости преобразуется в зависимость изменения относительной микротвердости от параметра, характеризующего нормированную толщину покрытия. В качестве нормирующего значения принимается величина предельного радиуса внедрения жесткого сферического штампа в поверхность слоистого тела. Фиг.2 иллюстрирует результат преобразования зависимости микротвердости от глубины внедрения для слоистых тел в зависимость относительной композиционной микротвердости от относительной толщины покрытия ( h a c ) .

Участок с возрастающими экспериментальными значениями относительной композиционной микротвердости поверхности с покрытием от относительной толщины покрытия аппроксимируем аналитической функцией, например линейного вида (или в виде полинома) (см. фиг 2):

H c H o = b + a ⋅ h ¯ ,             ( 1 )

где b, а - коэффициенты линейной функции, аппроксимирующей экспериментальные значения возрастающей ветви кривой изменения относительной композиционной твердости ( H c H o ) от относительной толщины покрытия ( h a c ) .

Параметр a_c аналитически связан с параметром, используемым при измерении твердости методом внедрения пирамидального индентора, - глубиной внедрения s. Покажем это. Для чего рассмотрим геометрические соотношения, характеризующие связь предельного радиуса отпечатка а_с, создаваемой сферой радиуса R на поверхности слоистой системы, с глубиной отпечатка от четырехгранной пирамиды. При внедрении в поверхность упругого жесткопластичного двухслойного полупространства жесткой сферы предельный радиус отпечатка а_с, соответствующий переходу от упругой деформации к чисто пластической, имеет место при среднем давлении в контакте, равном величине предельной твердости материала (Ланков А.А., Миронов В.А. Упругость, упругопластичностъ, пластичность в конструкционных средах. Тверь: ТГТУ (Тверской государственный технический университет), 1997. - 132 с.). Следовательно, для четырехгранной пирамиды с углом при вершине, равном 136° (пирамида Виккерса), глубина внедрения «s» связана с диагональю отпечатка «l» и предельным радиусом отпечатка а_с от сферы, вписанной в четырехгранную пирамиду, следующими известными зависимостями:

s = l 7 , l = 2 ⋅ 2 ⋅ a c .

После несложного преобразования указанных выше соотношений получаем выражение, связывающее параметр s h , характеризующий в безразмерном виде глубину внедрения жесткого пирамидального индентора в двухслойное полупространство, с параметром h a c , характеризующим в безразмерном виде толщину покрытия, в виде:

a c h = 2,5 ⋅ s h .

Известен аналитический способ определения теоретической композиционной твердости поверхности твердого тела с покрытием для случая внедрения сферического индентора (Воронин Н.А. Теоретическая