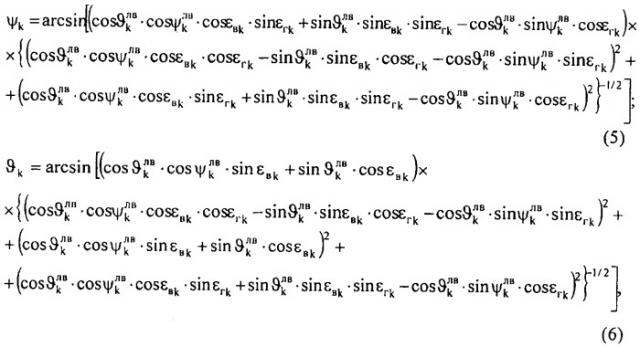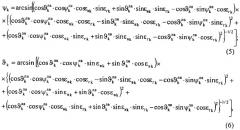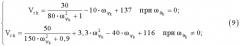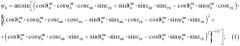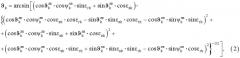Способ определения линейной скорости летательного аппарата на основе использования нерадиолокационной информации

Способ определения линейной скорости летательного аппарата на основе использования нерадиолокационной информации

Иллюстрации

Показать все

Реферат

Изобретение относится к области радиотехники, в частности, к радиоэлектронным системам измерения координат и параметров движения и может быть использовано в бортовых и наземных радиоэлектронных системах сопровождения (РЭСС).

Известен способ измерения радиальной составляющей линейной скорости летательного аппарата (ЛА) с использованием доплеровского смещения частоты (см. Финкельштейн, М.И. Основы радиолокации. - М.: Радио и связь, 1983. - 386 с).

Сущность данного способа состоит в следующем. Определение радиальной составляющей линейной скорости ЛА V_p основано на измерении радиолокационной станцией (РЛС) доплеровского частотного сдвига f_д принимаемых сигналов относительно колебаний, генерируемых передатчиком РЛС:

V p = 0 , 5 ⋅ λ ⋅ f д , ( 1 )

где f д = f 0 − f ; ( 2 )

λ - рабочая длина волны РЛС; f₀ - частота отраженных от ЛА колебаний; f - частота излучаемых РЛС колебаний.

Недостатком указанного способа является отсутствие возможности измерения линейной скорости ЛА, так как используемые в них физические явления позволяют измерять лишь радиальную составляющую линейной скорости ЛА.

Известен способ определения путевой скорости полета воздушной цели в наземной РЛС (Грачев В.В., Кейн В.М. Радиотехнические средства управления воздушным движением. - М.: Транспорт, 1975. - С.281-285).

Сущность способа состоит в следующем. Наземная РЛС с известными координатами, работающая в импульсном режиме, осуществляет круговое сканирование узким лучом диаграммы направленности антенны в горизонтальной плоскости. Измеренные РЛС координаты воздушной цели в полярной системе координат «азимут-дальность» переводятся в координаты (X, Y) прямоугольной системы координат. Для измерения путевой скорости воздушной цели вычисляют координаты (x_k-1, y_k-1) в (k-1)-й момент времени и координаты (x_k, y_k) воздушной цели в k-й момент времени, а модуль путевой скорости определяется из выражения:

V k = ( x k − x k − 1 ) 2 + ( y k − y k − 1 ) 2 t k − t k − 1 ,                        ( 3 )

где t_k и t_k-1 - k-й и (k-1)-й моменты времени соответственно; (t_k-t_k-1) - период измерения координат (x_k-1, y_k-1) и (x_k, y_k).

Недостатком данного способа является зависимость точности определения путевой скорости полета воздушной цели от точности вычисления координат (x_k-1, y_k-1) и (x_k, y_k), а также величины периода измерения координат (t_k-t_k-1).

Также известен способ определения путевой скорости воздушной цели в наземной радиолокационной станции (РЛС) (Князев И.Н., Князев Р.И. Способ определения путевой скорости воздушной цели в наземной радиолокационной станции. - Патент №2273032 от 27.03.06. Бюллетень №9. - 7 с.).

Сущность предлагаемого способа определения путевой скорости воздушной цели в наземной РЛС заключается в том, что измеряют частоту Доплера отраженных от движущейся цели сигналов в наземной РЛС f_дРЛС, а также частоту Доплера f_дR отраженных сигналов в дополнительной приемной позиции R, разнесенной в пространстве относительно наземной РЛС на базовое расстояние R_B, измеряют угол θ между направлениями «дополнительная приемная позиция R - цель Ц» и «дополнительная приемная позиция R - РЛС», угол γ между направлениями «РЛС - цель Ц» и «РЛС - дополнительная приемная позиция R», вычисляют бистатический угол β=180°-(θ+γ), а путевая скорость полета воздушной цели определяется по формуле:

V = λ ⋅ f д Р Л С 2 ⋅ c o s [ a r c t g ( f д R − f д Р Л С ⋅ c o s β f д Р Л С ⋅ s i n β ) ] ,                      ( 4 )

где λ - рабочая длина волны, используемая в наземной РЛС; f_дРЛС - частота Доплера, измеряемая в наземной РЛС; f_дR - частота Доплера, измеряемая в дополнительной приемной позиции R; β - бистатический угол между направлениями «РЛС - цель Ц» и «дополнительная приемная позиция R - цель Ц».

Недостатком данного способа является то, что для измерения путевой скорости воздушной цели необходимо использовать дополнительную радиолокационную приемную позицию, что существенно усложняет практическую реализацию способа.

Ни один из рассмотренных способов не может быть принят за прототип предлагаемого способа определения линейной скорости ЛА.

Техническим результатом предлагаемого способа является реализация возможности точного определения линейной скорости ЛА на основе использования нерадиолокационной информации, что снимает требования по точности радиолокационного измерения координат ЛА и наличию дополнительной радиолокационной приемной позиции, предъявляемые к существующим способам.

Сущность предлагаемого способа измерения линейной скорости ЛА V_k в k-й момент времени на основе использования нерадиолокационной информации заключается в том, что с помощью оптико-электронной системы (ОЭС), входящей в состав РЭСС, по двум последовательно полученным изображениям ЛА определяют значения углов рыскания ЛА ψ_k, ψ_k-1, и углов тангажа ЛА ϑ_k, ϑ_k-1, в k-й и (k-1)-й моменты времени, соответственно, используя выражения:

где ψ k л в и ϑ k л в - углы пространственной ориентации ЛА в лучевой системе координат РЭСС в k-й момент времени, информация о которых поступает от телевизионной системы (ТС), входящей в состав ОЭС; ε_гk и ε_вk - углы пеленга ЛА в горизонтальной и вертикальной плоскостях, соответственно, в k-й момент времени, информация о которых поступает от теплопеленгатора (ТП), входящего в состав ОЭС; на основе вычисленных значений углов рыскания ЛА ψ_k, ψ_k-1 и углов тангажа ЛА ϑ_k, ϑ_k-1, в k-й и (k-1)-й моменты времени, соответственно, определяют угловую скорость изменения угла рыскания ЛА ω_ψk и угловую скорость изменения угла тангажа ЛА ω_ϑk в k-й момент времени, используя выражения:

ω ψ k = | ψ k − ψ k − 1 Δ | ; ( 7 )

ω ϑ k = | ϑ k − ϑ k − 1 Δ | ; ( 8 )

где Δ - интервал обработки изображений ЛА ОЭС;

на основе вычисленных значений угловой скорости изменения угла рыскания ЛА ω_ψk и угловой скорости изменения угла тангажа ЛА ω_ϑk в k-й момент времени с помощью функциональных статистических зависимостей (функций регрессии) определяют проекции вектора линейной скорости ЛА на горизонтальную плоскость V_гk и вертикальную плоскость V_вk в k-й момент времени:

{ V г   k = 3 0 8 0 ⋅ ω ψ k 2 + 1 − 1 0 ⋅ ω ψ k + 1 3 7   п р и   ω ϑ k = 0 ; V г   k = 5 0 1 5 0 ⋅ ω ψ k 2 + 0 , 9 + 3 , 3 ⋅ ω ψ k 2 − 4 0 ⋅ ω ψ k + 1 1 6   п р и   ω ϑ k ≠ 0 ;              ( 9 )

{ V в   k = − 1 8 ⋅ a r c c t g ( 6 6 , 5 ⋅ ω ϑ k − 4 , 2 ) − 8 0 ⋅ ω ϑ k + 7 5     п р и   ω ψ k = 0 ; V в   k = − 2 4 ⋅ a r c c t g ( 1 7 , 5 ⋅ ω ϑ k − 1 , 4 ) − 3 0 ⋅ ω ϑ k + 8 5     п р и   ω ψ k ≠ 0 ;   ( 1 0 )

с использованием которых определяют значение линейной скорости ЛА в k-й момент времени:

V k = V г k 2 + V в k 2 .                    ( 1 1 )

Сущность способа поясняется следующим. Линейную скорость ЛА, движущегося по криволинейной траектории, можно описать выражением (Яворский Б.М., Детлаф А.А. Справочник по физике. - М.: Наука, 1985. - 512 с.):

V k = ω k ⋅ r k ,                   ( 1 2 )

где ω_k - абсолютное значение угловой скорости перемещения ЛА; r_k - радиус окружности, по дуге которой движется ЛА в k-й момент времени.

Так как ЛА может маневрировать и в горизонтальной, и в вертикальной плоскостях, то следует определять значения проекций вектора линейной скорости ЛА на горизонтальную V_гk и вертикальную V_вk плоскости:

V г   k = ω г k ⋅ r г k ;                ( 1 3 )

V в   k = ω в k ⋅ r в k ;                   ( 1 4 )

где ω_гk, ω_вk - абсолютные значения угловых скоростей перемещения ЛА в горизонтальной и вертикальной плоскостях, соответственно, в k-й момент времени; r_гk, r_вk - проекции радиуса окружности, по дуге которой движется ЛА в k-й момент времени, на горизонтальную и вертикальную плоскости, соответственно.

Абсолютные значения угловых скоростей перемещения ЛА в горизонтальной и вертикальной плоскостях являются ни чем иным, как абсолютными значениями угловых скоростей изменения угла поворота φ_k и угла наклона θ_k траектории ЛА ω_φk и ω_θk в k-й момент времени, соответственно:

ω г k = ω ϕ k ;                      ( 1 5 )

ω в k = ω θ k .                     ( 1 6 )

В РЭСС нет возможности измерять углы φ_k и θ_k, а, следовательно, и абсолютные значения угловых скоростей их изменения ω_φk и ω_θk. Однако есть возможность по получаемым от ОЭС в реальном масштабе времени изображениям сопровождаемого ЛА определять углы его рыскания ψ_k и тангажа ϑ_k, а значит и абсолютные значения угловых скоростей их изменения ω_ψk и ω_ϑk.

В силу малости углов атаки α_k и скольжения β_k при выполнении большинства маневров современными ЛА правомерно допущение о совпадении направления вектора линейной скорости ЛА и его продольной оси. Поэтому принимается, что φ_k=ψ_k, ω_φk=ω_ψk и θ_k=ϑ_k, ω_θk=ω_ϑk.

Тогда значения проекций вектора линейной скорости ЛА на горизонтальную плоскость V_гk и вертикальную плоскость V_вk в k-й момент времени определяются как:

V г   k = ω ψ k ⋅ r г k ;                       ( 1 7 )

V в   k = ω ϑ k ⋅ r в k .                      ( 1 8 )

Из выражений (17) и (18) видно, что при известных проекциях радиуса окружности, по дуге которой движется ЛА в k-й момент времени, на горизонтальную плоскость r_гk и вертикальную плоскость r_вk, проекции вектора линейной скорости ЛА на горизонтальную плоскость V_гk и вертикальную плоскость V_вk связаны детерминированной функциональной зависимостью с абсолютными значениями угловых скоростей изменения его угла рыскания ω_ψk и тангажа ω_ϑk, соответственно.

Однако в РЭСС информация о параметрах вращательного движения сопровождаемого ЛА r_гk и r_вk отсутствует. этом случае предполагается, что значения V_гk и V_вk являются возможными значениями соответствующих случайных величин (СВ) V_г и V_в, а значения ω_ψk и ω_ϑk возможными значениями соответствующих СВ ω_ψ и ω_ϑ. Тогда связь СВ V_г и V_в с соответствующими СВ ω_ψ и ω_ϑ можно описать статистическими функциональными зависимостями - функциями регрессии (Елисеева И.И., Юбзашев М.М. Общая теория статистики / под ред. чл.-корр. РАН И.И. Елисеевой. - М.: Финансы и статистика, 1995. - 368 с.):

V ¯ г = f ( ω ψ ) ;                     ( 1 9 )

V ¯ в = f ( ω ϑ ) ,                         ( 2 0 )

где V ¯ г и V ¯ в - условные средние СВ V_г и V_в (средние арифметические значения СВ V_г и V_в при фиксированных значениях СВ ω_ψ и ω_ϑ, соответственно).

Исследование вида функций регрессии (19) и (20) проводилось на основе сформированных по реальной полетной информации выборок СВ V_г, V_в, ω_ψ и ω_ϑ. Кроме того, для исследования связи (19) осуществлялось разбиение выборок СВ V_г и ω_ψ в зависимости от условия: ω_ϑ=0 (маневр ЛА осуществляется в горизонтальной, либо наклонной плоскостях) или ω_ϑ≠0 (маневр ЛА осуществляется по пространственной траектории). По аналогии, для исследования связи (20) проводилось разбиение выборок СВ V_в и ω_ϑ в зависимости от условия: ω_ψ=0 (маневр ЛА осуществляется в вертикальной плоскости) или ω_ψ≠0 (маневр ЛА осуществляется по пространственной траектории).

Аппроксимация полученных зависимостей V ¯ г от ω_ψ и V ¯ в от ω_ϑ математическими функциями осуществлялась с учетом минимизации среднеквадратической погрешности приближения значений математических функций к значениям функций регрессии, полученным в результате исследований. В результате были получены выражения вида (9)-(10).

Один из вариантов программной реализации предлагаемого способа представлен на фигуре 1 при помощи логической схемы алгоритма функционирования программы определения линейной скорости ЛА на основе использования нерадиолокационной информации.

Логическая схема состоит из блока «Данные» I; блока «Подготовка» II; блоков «Процесс» III, VI-X; блоков «Решение» IV, V; блока «Запоминаемые данные» XI; блоков «Оперативное запоминающее устройство» XII, XIII.

В блоке I устанавливаются исходные значения параметров Δ, ϑ₀ и ψ₀. На вход блока III поступают значения ψ k л в , ϑ k л в , ε_гk и ε_вk в k-й момент времени от внешних источников информации. Вычисление выражений, определяющих значения ψ_k, ϑ_k, ω_ψk и тангажа ω_ϑk в k-й момент времени производится в блоке III. В блоке IV в зависимости от выполнения условия ω_ϑk=0 принимается решение о вычислении значения V_гk в k-й момент времени в блоке VI или блоке VII. В блоке V в зависимости от выполнения условия ω_ψk=0 принимается решение о вычислении значения V_вk в k-й момент времени в блоке VIII или блоке IX. Вычисления в блоке VI (блоке VII) и в блоке VIII (блоке IX) осуществляются параллельно. Результаты вычислений блока VI (блока VII) и блока VIII (блока IX) используются в блоке Х для вычисления значения V_k.

Результаты вычислений блока III и блока Х запоминаются в блоке XI для использования на следующем шаге вычислений в (k+1)-й момент времени (блок II). Вычисленное в блоке Х значение V_k в k-й момент времени запоминается в оперативном запоминающем устройстве (блок XII). Функционирование блоков III-XII осуществляется до момента сброса сопровождения (блок XIII).

Способ определения линейной скорости летательного аппарата на основе использования нерадиолокационной информации, заключающийся в том, что с помощью оптико-электронной системы по двум последовательно полученным изображениям летательного аппарата определяют значения углов рыскания летательного аппарата ψ_k, ψ_k-1 и углов тангажа летательного аппарата ϑ_k, ϑ_k-1 в k-й и (k-1)-й моменты времени, соответственно, используя выражения: ψ k = a r c s i n [ ( c o s ϑ k л в ⋅ c o s ψ k л в ⋅ c o s ε в k ⋅ s i n ε г k + s i n ϑ k л в ⋅ s i n ε в k ⋅ s i n ε г k − c o s ϑ k л в ⋅ s i n ψ k л в ⋅ c o s ε г k ) ⋅ { ( c o s ϑ k л в ⋅ c o s ψ k л в ⋅ c o s ε в k ⋅ c o s ε г k − s i n ϑ k л в ⋅ s i n ε в k ⋅ c o s ε г k − c o s ϑ k л в ⋅ s i n ψ k л в ⋅ s i n ε г k ) 2 + + ( c o s ϑ k л в ⋅ c o s ψ k л в ⋅ c o s ε в k ⋅ s i n ε г k + s i n ϑ k л в ⋅ s i n ε в k ⋅ s i n ε г k − c o s ϑ k л в ⋅ s i n ψ k л в ⋅ s i n ε г k ) 2 } − 1 / 2 ] ;   ( 1 ) ϑ k = a r с s i n [ ( c o s ϑ k л в ⋅ c o s ψ k л в ⋅ s i n ε г k + s i n ϑ k л в ⋅ c o s ε в k ) ⋅ { ( c o s ϑ k л в ⋅ c o s ψ k л в ⋅ c o s ε в k ⋅ c o s ε г k − s i n ϑ k л в ⋅ s i n ε в k ⋅ c o s ε г k − c o s ϑ k л в ⋅ s i n ψ k л в ⋅ s i n ε г k ) 2 + + ( c o s ϑ k л в ⋅ c o s ψ k л в ⋅ s i n ε в k + s i n ϑ k л в ⋅ c o s ε в k ) 2 + + ( c o s ϑ k л в ⋅ c o s ψ k л в ⋅ c o s ε в k ⋅ s i n ε г k + s i n ϑ k л в ⋅ s i n ε в k ⋅ s i n ε г k − c o s ϑ k л в ⋅ s i n ψ k л в ⋅ c o s ε г k ) 2 } − 1 / 2 ] ,   ( 2 ) где ψ k л в и ϑ k л в - углы пространственной ориентации летательного аппарата в лучевой системе координат радиоэлектронной системы сопровождения в k-й момент времени, информация о которых поступает от телевизионной системы, входящей в состав оптико-электронной системы;ε_гk и ε_вk - углы пеленга летательного аппарата в горизонтальной и вертикальной плоскостях, соответственно, в k-й момент времени, информация о которых поступает от теплопеленгатора, входящего в состав оптико-электронной системы,на основе вычисленных значений углов рыскания летательного аппарата ψ_k, ψ_k-1 и углов тангажа летательного аппарата ϑ_k, ϑ_k-1, в k-й и (k-1)-й моменты времени, соответственно, определяют угловую скорость изменения угла рыскания летательного аппарата ω_ψk и угловую скорость изменения угла тангажа летательного аппарата ω_ϑk в k-й момент времени, используя выражения: ω ψ k = | ψ k − ψ k − 1 Δ | ;   ( 3 ) где Δ - интервал обработки изображений летательного аппарата оптико-электронной системой;на основе вычисленных значений угловой скорости изменения угла рыскания летательного аппарата ω_ψk и угловой скорости изменения угла тангажа летательного аппарата ω_ϑk в k-й момент времени с помощью функциональных статистических зависимостей (функций регрессии) определяют проекции вектора линейной скорости летательного аппарата на горизонтальную плоскость V_гk и вертикальную плоскость V_вk в k-й момент времени: { V г k = 30 80 ⋅ ω ψ k 2 + 1 − 10 ⋅ ω ψ k + 137   п р и       ω ϑ k = 0 ; V г k = 50 150 ⋅ ω ψ k 2 + 0,9 + 3,3 ⋅ ω ψ k 2 − 40 ⋅ ω ψ k + 116   п р и       ω ϑ k ≠ 0 ;    ( 5 ) { V в k = − 18 ⋅ a r c c t g ( 66,5 ⋅ ω ϑ k − 4,2 ) − 80 ⋅ ω ϑ k + 75     п р и       ω ψ k = 0 ; V в k = − 24 ⋅ a r c c t g ( 17,5 ⋅ ω ϑ k − 1,4 ) − 30 ⋅ ω ϑ k + 85     п р и      ω ψ k ≠ 0 ;   ( 6 ) с использованием которых определяют значение линейной скорости летательного аппарата в k-й момент времени: V k = V г k 2 + V в k 2 .               ( 7 )