Рекурсивный цифровой фильтр

Рекурсивный цифровой фильтр

Иллюстрации

Показать все

Реферат

Изобретение относится к области обработки цифровых данных с помощью электрических устройств, в частности, может использоваться в электрических автоматических микропроцессорных регуляторах, цифровых интегрирующих, апериодических и дифференцирующих звеньях, а также в любых цифровых алгоритмах и устройствах обработки последовательных цифровых отсчетов, в которых используется операция деления на постоянный целочисленный делитель.

Цель изобретения - повышение точности цифровой фильтрации.

В качестве ближайшего аналога принято изобретение SU 1626335 А1 от 20.09.1988, МПК Н03Н 17/04, опубликованное 07.02.1991 в Бюл. №5, в котором приводится реализация цифрового рекурсивного фильтра низких частот и цифрового интегратора. Особенностью описанных устройств является применение накапливающего сумматора, на первый вход которого подается цифровое значение входного сигнала, на второй вход подается задержанный на один такт остаток от деления, а сигнал с выхода подается на вход блока деления.

Недостатком изобретения SU 1626335 является то, что максимальная относительная погрешность в одном такте целочисленного деления по сравнению с идеальным результатом составляет (1):

E ( 1 ) m a x = N − 1 N ,             ( 1 )

где N>0 - величина целочисленного делителя (постоянный коэффициент).

Предлагаемое изобретение позволяет уменьшить максимальную относительную погрешность в одном такте целочисленного деления в два раза (2):

E ( 2 ) m a x = N − 1 2 N .             ( 2 )

Технический результат достигается с помощью ввода дополнительного блока коррекции частного и остатка, вход которого соединен со вторым выходом блока деления на постоянный коэффициент, а первый выход соединен с входом второго блока задержки, в третьем сумматоре добавлен третий вход, который соединен со вторым выходом блока коррекции частного и остатка.

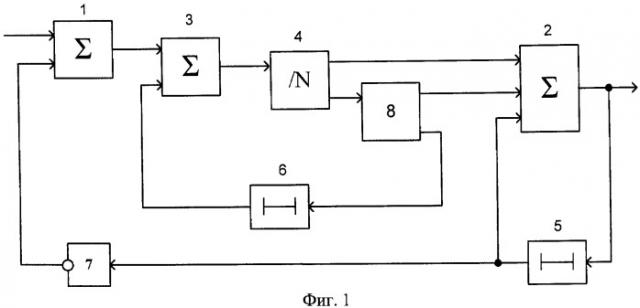
На фиг.1 приведена электрическая структурная схема рекурсивного цифрового фильтра. Рекурсивный цифровой фильтр содержит первый, второй и третий сумматоры 1-3, блок целочисленного деления на постоянный коэффициент 4, первый и второй блоки задержки 5, 6; блок инверторов 7; блок коррекции частного и остатка 8.

При отсутствии элементов 1 и 7 (фиг.1) рекурсивный цифровой фильтр представляет собой интегратор с коэффициентом α = 1 N , сигнал на выходе которого в каждом такте n описывается рекуррентной формулой (3);

y n = y n − 1 + α ⋅ x n ,           ( 3 )

где x_n - цифровое значение входного сигнала.

Если значения x_n и y_n представлены в памяти вычислительного устройства целыми числами конечной разрядности, а вычисления по формуле (3) производятся по правилам целочисленной арифметики, результат операции α ⋅ x n = x n N представляется целым N числом, а остаток отбрасывается. При больших значениях N ошибка округления на каждом шаге может достигать значительной величины и накапливаться в ходе вычислений по рекуррентной формуле (3). Для компенсирования ошибки округления в SU 1626335 предложено интегрирование выполнять согласно рекуррентной формуле (4):

y n = y n − 1 + x n + δ n − 1 N ,         ( 4 )

где δ_n-1 - остаток деления x_n-1, на N, при этом результат операции деления представляется целым числом, а дробная часть отбрасывается.

При вычислениях по формуле (4) на каждом шаге, вследствие операции отбрасывания дробной части, может возникнуть расхождение с идеальным (аналоговым) вычислением и представлением чисел с неограниченной разрядностью. Максимальная относительная погрешность операции деления на N определяется по формуле (1).

Если в (4) операцию деления с отбрасыванием дробной части частного заменить округлением до ближайшего целого, то максимальную относительную погрешность можно снизить в два раза согласно формуле (2). Операция округления реализуется вводом дополнительного блока коррекции частного и остатка. Направление коррекции частного на каждом шаге определяется в зависимости от величины остатка δ_n, и осуществляется по следующим правилам. Если значение целочисленного остатка δ_n превышает половину величины делителя N, то коррекцию частного производят в большую сторону, а частное увеличивают на одну единицу младшего значащего разряда (МЗР), а от остатка вычитают величину делителя. Если остаток δ_n отрицательный и по абсолютной величине превышает половину величины делителя N, то коррекцию частного производят в сторону меньшего отрицательного целого, при этом частное уменьшают на одну единицу МЗР, а к остатку прибавляют величину делителя. В остальных случаях остаток и частное не корректируют.

Алгоритм работы блока коррекции частного и остатка определяется формулами (5):

{ q n = z n + 1 ;   r n = δ n − N ,   е с л и   δ n > N 2 ; q n = z n − 1 ;   r n = δ n + N ,   е с л и   δ n < − N 2 ;                   ( 5 )

где δ_n - целочисленный остаток, полученный на шаге n; z n = [ x n + δ n − 1 N ] - целочисленное частное, полученное на шаге n; q_n - откорректированное частное; r_n - откорректированный остаток.

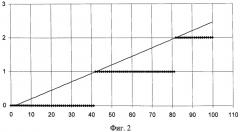
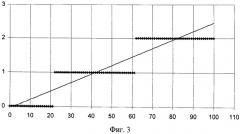
В качестве поясняющего примера на фиг.2, 3 приведены диаграммы, показывающие результат работы интеграторов, реализованных по схеме ближайшего аналога SU 1626335 (фиг.2) и предлагаемого изобретения (фиг.3). По оси абсцисс отображены номера тактов вычислений, по оси ординат - значения выходов интеграторов. Непрерывной линией показан сигнал на выходе идеального интегратора, точками - его цифровых реализации. В расчетах использовались следующие параметры: коэффициент каждого интегратора α = 1 40 , начальные условия: y₀=0. Входной сигнал был представлен последовательностью: х=0, 0, 1, 1, 1, ….

Предлагаемое изобретение может быть реализовано как аппаратно, так и программно. Все элементы устройства выполняют операции над целыми числами ограниченной разрядности в какой-либо позиционной системе счисления с положительным целым основанием.

Рекурсивный цифровой фильтр, содержащий последовательно соединенные первый блок задержки, блок инверторов и первый сумматор, второй вход которого является входом рекурсивного цифрового фильтра, выходом рекурсивного цифрового фильтра является вход первого блока задержки, а также последовательно соединенные второй блок задержки, второй сумматор, блок деления на постоянный коэффициент и третий сумматор, второй вход второго сумматора соединен с выходом первого сумматора, второй вход третьего сумматора соединен с выходом первого блока задержки, отличающийся тем, что, с целью повышения точности фильтрации, введен блок коррекции частного и остатка, вход которого соединен со вторым выходом блока деления на постоянный коэффициент, а первый выход соединен с входом второго блока задержки, в третьем сумматоре добавлен третий вход, который соединен со вторым выходом блока коррекции частного и остатка.