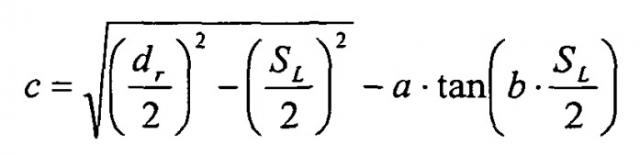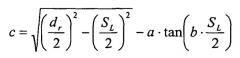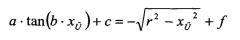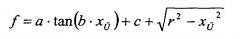Зубчатое колесо

Зубчатое колесо

Иллюстрации

Показать все

Реферат

Изобретение касается зацепления зубчатого колеса, имеющего большое количество зубьев, согласно ограничительной части пункта 1 формулы изобретения.

Из DE 10 2006 015 521 B3 известно зубчатое колесо с эвольвентным профилем, полученными методом обкатки. При этом предметом указанного документа является, в частности, так называемая область ножки зуба, то есть область, которая соединяет друг с другом отдельные зубья зубчатого колеса с эвольвентным профилем. В указанном документе с целью предоставить зубчатые зацепления, одинаково работоспособные в обоих направлениях движения, предлагается область ножки зуба, которая, в отличие от обычных закруглений, полученных методом обкатки, закругляется в форме эллипса. Такие зубчатые колеса благодаря эллиптическому закруглению области ножки зуба обладают более высокой несущей способностью, чем зубчатые колеса с радиальным закруглением.

Исходя из этого известного ранее уровня техники, задачей настоящего изобретения является предоставить зубчатое колесо с полученными методом обкатки зубьями, которое позволит еще больше повысить прочность области ножки зуба так, чтобы зубчатое колесо при одинаковой прочности могло быть выполнено с меньшими размерами или - при сравнимом конструктивном размере - со значительным увеличением прочности.

Эта задача в соответствии с изобретением решается с помощью признаков, приведенных в отличительной части пункта 1 формулы изобретения.

Было обнаружено, что выполнение области ножки зуба в форме, описываемой тангенсоидой, которая тангенциально непрерывно (tangetialstetig) выходит из расположенной над ней формы боковой поверхности профиля зуба в активной области, и в своею очередь тангенциально непрерывно переходит в дугу окружности впадины, которая в свою очередь по касательной прилегает к окружности впадин зубчатого колеса, позволяет значительно увеличить прочность ножки зуба.

При этом проведенные исследования показали, что такое включение тангенсоиды между дугой окружности впадины и формой боковой поверхности профиля зуба в активной области дает возможность расчетного увеличения прочности ножки зуба до 30%, в отличие от традиционного зубчатого колеса, полученного методом обкатки.

Благодаря симметрии боковой поверхности профиля двух соседних зубьев по отношению друг к другу достаточно определить форму одной из боковых поверхностей профиля зуба и затем перенести ее путем зеркального отражения относительно оси симметрии на противоположную область. Благодаря тому, что дуга окружности впадин в нижней точке впадины тангенциально прилегает к окружности впадин, и ось симметрии проходит через эту нижнюю точку впадины, с помощью простой комбинации тангенсоиды с дугой окружности впадины до нижней точке впадины и путем последующего зеркального отображения двух этих функций можно сформировать всю область ножки зуба так, чтобы ее прочность увеличилась.

Причем определить эти функциональные возможности соответственно просто и эффективно можно в нормальном сечении указанным образом, так как переходы функций друг в друга можно представить математически, так что необходимо только выбрать угол и радиус дуги окружности впадины в зависимости от параметров конструкции. Возникающая при этом форма области ножки зуба или, соответственно, впадины между зубьями зубчатого колеса может затем быть перенесена в нормальное сечение различных зубьев зубчатых колес. Так, например, торцовые зубчатые зацепления с прямыми, косыми или спиральными зубьями также позволяют использовать предлагаемую изобретением форму области ножки зуба и получить связанное с этим увеличение прочности, так же как и зубчатые зацепления, например, конических зубчатых колес или зубчатых колес другого рода.

В принципе, предлагаемая изобретением форма ножки зуба может, конечно, использоваться и в зубчатых рейках, конических зубчатых колесах, косозубых колесах, корончатых зубчатых колесах, винтовых зубчатых колесах или червячных колесах, причем форму ножки зуба тогда следует определить в соответствующем нормальном сечении и затем, например, у однозаходных и многозаходных червячных колес по длине развернутого как одно целое зуба, выполнить соответствующие изменения, разумеется, с учетом обычно изменяющейся геометрии самого зуба, то есть, например, высоты зуба и ширины зуба.

То есть предлагаемое изобретением зубчатое зацепление в принципе может быть реализовано в различных зубчатых колесах и в снабженных зубьями элементах. При этом возможна также комбинация с любыми формами боковой поверхности профиля зуба в активной области.

Особенно предпочтительно, однако, применение с формой боковой поверхности профиля зуба, выполненной в виде циклоидальной кривой (эвольвенты или октоиды), в частности, в виде эвольвентной формы боковой поверхности профиля зуба. Этот распространенный в машиностроении общеизвестный тип зубчатого зацепления особенно хорошо подходит для варианта осуществления области ножки зуба, предлагаемого изобретением. Наибольшие возможности увеличения прочности за счет новой формы области ножки зуба были обнаружены у такого рода зубчатых колес с эвольвентным зацеплением.

Ниже с помощью фигур на одном из примеров осуществления описан внешний вид и функциональные возможности новой формы ножки зуба на примере одного зуба или, соответственно, впадины между зубьями зубчатого колеса с эвольвентным зацеплением. Но в принципе, этот вариант осуществления области ножки зуба, как уже подробно излагалось, может также применяться к различным видам зубчатых колес и зубчатых зацеплений.

Показано:

Фиг. 1 - вид в нормальном сечении зубчатого колеса с эвольвентными зубьями при торцевом зацеплении;

Фиг. 2 - вариант осуществления области ножки зуба в зубчатом колесе, показанном на фиг. 1, аналогично изобретению; и

Фиг. 3 - детальное изображение математических величин для определения необходимых функций для предлагаемого изобретением выполнения области ножки зуба.

На фиг. 1 изображена впадина 1 зуба в нормальном сечении. При этом в качестве базовых параметров отмечены координаты x, y, причем ось y одновременно является осью симметрии впадины 1 зуба. При этом указанные участки двух зубьев 2 в части 3 своей головки ограничены не изображенной здесь окружностью выступов. Упомянутая здесь для примера форма 4 боковой поверхности профиля зуба представляет собой эвольвентную форму боковой поверхности профиля зуба, которая используется до диаметра d_N так называемой окружности активных точек не изображенной здесь боковой поверхности профиля зуба, входящего в зацепление с этим зубчатым колесом сопряженного зубчатого колеса или, соответственно, зубчатого элемента. Этот участок между окружностью головок в области головок 3 зубьев 2 и окружностью активных точек (диаметр d_N) далее будет называться активной областью. Кроме того, следует еще указать на наименьший диаметр, до которого погружается зуб входящего в зацепление с этим зубчатым колесом сопряженного зубчатого колеса или, соответственно, зубчатого элемента. Этот диаметр обычно называется диаметром d_FR окружности выступов сопряженного колеса.

Примыкающая к нему в направлении центра зубчатого колеса область между окружностью активных точек (d_N) и нижней точкой впадины 1 зуба, в которой располагается так называемая окружность d_F впадин, далее будет называться областью ножки впадины 1 зуба. Точка пересечения оси y симметрии с окружностью d_F впадин является при этом нижней точкой FP впадины 1 зуба.

Названные выше величины представляют собой величины, используемые обычно для всех зубчатых колес, на которые будет опираться последующее детальное описание предлагаемого изобретением варианта осуществления области ножки зуба, которая здесь уже изображена в соответствии с изобретением.

Дополнительно в изображенном здесь примере эвольвентной формы 4 боковой поверхности профиля зуба важными являются другие величины. Так, на фиг. 1 изображена так называемая основная окружность d_b, которая является важной для конструкции формы боковой поверхности профиля эвольвентного зацепления. Кроме того, необходимо еще коротко упомянуть обычно используемый модуль m, который получается путем деления не изображенного здесь диаметра делительной окружности на количество зубьев или, соответственно, деления шага p на число π.

Кроме того, на фиг. 1 показан диаметр или, соответственно, радиус, который важен для данного изобретения и будет обозначаться релевантным диаметром d_r. Этот релевантный диаметр d_r описывает в изображенном здесь примере осуществления переход формы 4 боковой поверхности профиля зуба в активной области в предлагаемую изобретением форму боковой поверхности профиля зуба в области ножки зуба. Этот переход у традиционных зубчатых зацеплений известен также как окружность модификации (Formkreis). Релевантный диаметр может теоретически равняться диаметру d_N окружности активных точек (Nutzkreisdurchmesser). Однако, в общем случае он выбирается несколько меньше, чтобы обеспечить разумную надежность в отношении допусков изготовления и допусков установки зубчатых колес. В изображенном здесь примере осуществления релевантный диаметр d_r выбран как среднее арифметическое между диаметром d_N окружности активных точек и диаметром d_FR окружности выступов (Freikreis) сопряженного колеса, так что образуется определенное безопасное расстояние между релевантным диаметром d_r и диаметром d_N окружности активных точек. Благодаря этому обеспечивается, что не изображенный здесь зуб входящего в зацепление с зубчатым колесом сопряженного зубчатого элемента в любом случае пройдет по расчетной форме 4 боковой поверхности профиля зуба, то есть здесь по эвольвенте, а не войдет в зацепление с боковой поверхностью профиля в области ножки зуба, имеющей форму согласно изобретению, создавая при этом нагрузку.

На фиг. 2 более подробно поясняется форма ножки зуба в предлагаемом изобретением варианте осуществления. При этом уже названные на фиг. 1 элементы на фиг. 2 обозначены теми же позициями. Из приведенных на фиг. 1 диаметров на фиг. 2 изображен только релевантный диаметр d_r. Как уже было упомянуто, форма 4 боковой поверхности профиля зуба в активной области в настоящем примере осуществления из соображений надежности и в связи с допусками переходит в области релевантного диаметра d_r в предлагаемый изобретением вариант осуществления формы ножки зуба в области ножки зуба тангенциально непрерывно. В точке P, в которой диаметр d_r пересекает боковую поверхность 4 профиля зуба, происходит этот переход от эвольвентной формы 4 боковой поверхности профиля зуба к тангенсоиде в обозначенной позицией 5 области формы боковой поверхности профиля зуба. На фиг. 2 тангенс, проходящий в области 5 формы боковой поверхности профиля зуба в направлении центра зубчатого колеса, то есть центра координат, продолжен. Этот участок тангенсоиды 5` пересекает при этом ось y в области, расположенной ниже нижней точки FP впадины, то есть при математическом условии x=0 тангенс на пересечении с осью симметрии y имеет соответствующий угол подъема. Угол подъема относительно оси x на фиг. 2 при этом обозначен углом γ. Относительно самой оси симметрии получается, таким образом, угол 90° - γ. Причем этот угол γ будет важен для конструирования, которое будет поясняться позднее, или, соответственно, для выбора конкретной тангенсоиды.

Кроме того, видно, что тангенсоида в точке перехода ÜP переходит в дугу 6 окружности впадины. И этот переход между дугой 6 окружности впадины и используемой областью тангенсоиды 5 выполнен с общим тангенсом. Тогда дуга 6 окружности впадины касается окружности впадин d_f в нижней точке FP впадины, то есть в точке пересечения окружности впадин d_f с осью симметрии y.

Математическая функция тангенса относительно центра координат, совпадающего с центром зубчатого колеса и проходящей соответственно симметрично каждой впадине 1 зуба оси симметрии y описывается с помощью следующего уравнения:

y(x)=a·tan(b·x)+c (уравн.1)

Чтобы однозначно определить эту функцию, необходимы три краевых условия, которые формулируются следующим образом:

(1) Переход от эвольвенты к тангенсоиде происходит тангенциально непрерывно.

(2) Угол подъема тангенсоиды в точке пересечения с осью симметрии y (то есть при x=0) определяется углом γ. Этот угол может позднее выбираться свободно в определенных конструктивных границах, о чем ниже будет сказано более подробно.

(3) Точка перехода от эвольвенты к тангенсоиде находится на релевантном диаметре d_r, который, по сути, может быть выбран любым, однако в любом случае должен быть меньше диаметра d_N окружности активных точек, как уже было сказано выше.

Примыкающая к этому тангенсу дуга 6 окружности впадины в общей форме выражается следующим уравнением:

r²=(x-e)+(y-f)² (уравн.2)

При этом радиус r может быть выбран любым. Центр должен при этом лежать на оси симметрии y, то есть оси ординат системы координат. Соответственно этому значение e получается e=0. Кроме того, для уравнения окружности необходимо еще и другое краевое условие:

(4) Переход к тангенсоиде в точке перехода ÜP происходит тангенциально непрерывно.

Форма боковой поверхности профиля зуба в области ножки зуба ниже будет описана в общей математической форме, при этом важные величины, которые еще не пояснялись на приведенных ранее фигурах, указаны на фиг. 3. Сначала осуществляется определение координат точки P примыкания эвольвенты.

Эта точка лежит на диаметре d_r. Чтобы определить ширину S_L (по хорде) впадины зуба, необходима толщина s_r зуба в радианах, которая определяется следующим образом (s = толщина зуба на делительной окружности; d = диаметр делительной окружности):

(уравн. 3)

α_r представляет собой угол зацепления на диаметре d_r. При этом угол зацепления α_r задается неявным образом при выборе эвольвенты. Оказалось, что предлагаемое изобретением увеличение прочности наступает, начиная с угла зацепления α_r, равного от 4° до 5°. Таким образом, угол зацепления α_r должен в любом случае выбираться больше 4°, предпочтительно больше 7°. В отличие от этого, α означает угол зацепления на делительной окружности, который у большинства зубчатых колес обычно составляет 15-25°, предпочтительно около 20°.

Тогда ширина s_L впадины зуба в радианах вычисляется следующим образом:

(уравн. 4)

Отсюда можно найти ширину впадины зуба (по хорде):

(уравн. 5)

Тогда координата x точки P будет равна:

(уравн. 6)

Координата y находится из уравнения Пифагора:

(уравн. 7)

Чтобы обеспечить тангенциальную непрерывность в точке P, необходимо знать угол подъема φ эвольвенты в точке P. Этот угол складывается из угла зацепления α_r и половины угла раскрытия впадины зуба:

(уравн. 8)

Теперь можно с помощью краевых условий определить коэффициенты a и b, а также составляющую с. Из краевого условия (1) следует:

(уравн. 9)

Из краевого условия (2) следует:

(уравн. 10)

Из краевого условия (3) следует:

(уравн. 11)

Тогда для a, b и c получается:

(уравн. 12)

(уравн. 13)

(уравн. 14)

Угол γ может быть выбран соответствующим образом. Чтобы добиться улучшения по сравнению с традиционными зубчатыми зацеплениями, он должен быть выбран в любом случае меньше 65°. Однако, в первом приближении оптимальное значение равно или меньше 45°. Особенно предпочтительным оказался выбор угла по приведенной ниже зависимости, выраженной уравнением 15, причем хорошие результаты можно получить в поле допусков +/-20% в области этого значения γ.

(уравн. 15)

Общее уравнение окружности должно быть сначала приведено в форму g(x).

(уравн. 16)

Так как точка центра окружности лежит на оси y, можно подставить e=0. Требуется нижняя дуга окружности, поэтому перед корнем должен быть знак минус. Следовательно:

(уравн. 17)

Теперь можно определить d. Из краевого условия (4) получается следующая зависимость. Производные тангенсоиды и круговой функции в переходном месте в точке перехода ÜP при x_Ü должны иметь одинаковую величину.

(уравн. 18)

Отсюда следует уравнение, с помощью которого можно определить место перехода x_Ü:

(уравн. 19)

Имея x_Ü, теперь можно определить f. Для этого обе функции приравниваются друг к другу в точке x_Ü:

(уравн. 20)

Следовательно, для f получается:

(уравн. 21)

Итак, геометрия впадины зуба в области ножки зуба в общем случае может быть выражена следующим образом:

где: a находится из уравнения (уравн.12)

b находится из уравнения (уравн.13)

c находится из уравнения (уравн.14)

d находится из уравнения (уравн.21)

x_Ü находится из уравнения (уравн.19)

При этом функция для отрицательных аргументов получается просто путем зеркального отображения относительно оси ординат, так как эта ось ординат одновременно является осью симметрии Y впадины 1 зуба.

Как следует из подробно рассмотренной выше математической зависимости, теперь конструктору такой формы ножки зуба остается только выбрать угол γ, а также радиус r дуги 6 окружности. Для идеального выбора угла γ выше в уравнении (уравн. 15) уже имеется соответствующая рекомендация.

Для радиуса r дуги 6 окружности впадины оптимальными оказались значения, которые находятся в диапазоне 0,1-0,6-кратного модуля m. Предпочтительно эти значения находятся в диапазоне 0,3-0,4 модуля m. Другое улучшение достигается при ссылке на участок ширины S_L впадины зуба по хорде. Для радиуса R при этом оптимальными оказались значения 0,1-0,6 ширины S_L впадины зуба. Предпочтительно эти значения находятся в диапазоне 0,3-0,4 ширины S_L впадины зуба. В приведенном ниже примере расчет осуществлялся исходя из радиуса r=0,3 S_L, это значение следует по возможности выбирать как особенно предпочтительное значение.

Проведенные на основании этих значений расчеты методом конечных элементов дали увеличение прочности ножки зуба до 30% по сравнению с традиционными формами ножки зуба.

Пример значений, которые были выбраны в качестве примера из названных диапазонов значений, рассматривается ниже. При этом выбранные наименования и буквенные обозначения формул являются для зубчатых колес общеупотребительными и общеизвестными.

Зубчатое колесо I имеет следующие параметры:

модуль m=4 мм.

Количество зубьев z₁=53.

Смещение профиля x₁=0.

Угол зацепления на делительной окружности α=20°.

Чтобы определить диаметр d_N окружности активных точек и диаметр d_FR окружности выступов сопряженного колеса зубчатого колеса I, необходимы параметры второго входящего в зацепление с зубчатым колесом I зубчатого колеса II и расстояние между осями зубчатых колес I, II.

Количество зубьев z₂=19.

Смещение профиля x₂=0,6.

Расстояние между осями a=146,4 мм.

Для сравнения берется вариант зубчатого колеса, полученного методом обкатки. Форма ножки создается с помощью червячной фрезы со следующими параметрами:

коэффициент высоты головки h_aPO*=1,3889.

Коэффициент закругления головки ρ_aPO=0,25

(как принято и обозначено *, соответственно отнесенный к модулю m).

Угол протуберанца α_ρm0=10°.

Величина протуберанца ρ_m0=0,26 мм.

Припуск на обработку перед шлифованием выбирается q=0,16 мм, соответственно остаточная величина протуберанца получается равной 0,1 мм.

Для этого зубчатого зацепления получаются следующие входные величины для расчета кривой ножки:

диаметр окружности зацепления: d_N1=207,764 мм.

Диаметр окружности выступов сопряженного колеса d_FR=204,000 мм.

Диаметр перехода от эвольвенты к тангенсоиде (среднее арифметическое d_N1 и d_FR): d_r=205,88 мм.

Ширина впадины зуба (по хорде) к d_r: S_L=4,204 мм.

Угол подъема эвольвенты в точке перехода от эвольвенты к тангенсоиде: φ=74,2°.

Чтобы однозначно определить кривую ножки, не хватает еще данных угла подъема тангенсоиды в точке x=0 (γ) и радиуса r. Для угла γ можно в соответствии с уравнением (уравн. 15) принять следующую зависимость:

Радиус закругления r дуги 6 окружности впадины идеален, когда - как было изложено выше - выполняется следующая зависимость:

r = 0,35·S_L

Для данного примера, таким образом, получается:

γ=27°,

r=1,5 мм.

Коэффициенты и составляющие тангенсоиды и круговой функции получаются здесь следующие:

коэффициент a=0,30626.

Коэффициент b=0,63469976.

Составляющая c=101,64979.

Составляющая f=103,32733.

Пределы для γ у этого зубчатого колеса принимают следующие значения:

γ_min=11°,

γ_max=65°.

За пределами этого диапазона при новой форме ножки зуба, по сравнению с вышеназванным вариантом, изготовленным с помощью червячной фрезы, уменьшения напряжений и вместе с тем увеличения прочности ножки зуба не происходит.

Нижний предел радиуса в этом примере составляет r_min=0,5 мм, верхний предел r_max=2,1 мм. Это не предел, обусловленный напряжениями, а геометрический предел. Потому что этот радиус представляет собой практически полное закругление, которое, однако, имеет еще меньшие напряжения, чем сравнительный вариант, изготовленный с помощью червячной фрезы, однако более высокие, чем при оптимальных значениях γ и r.

По сравнению с традиционным зубчатым колесом, изготовленным методом обкатки, у приведенного в этом примере зубчатого колеса I возможно увеличение прочности ножки зуба на величину, составляющую до 30%.

Изготовление таких зубчатых колес может осуществляться, например, на программируемых фрезеровальных станках с многоосным управлением перемещениями или с помощью предназначенных для этого соответствующих предлагаемой изобретением форме ножки зуба зубофрезерных станках.

1. Зубчатое колесо, имеющее большое количество зубьев; причем боковые поверхности профиля зубьев имеют активную область и область ножки зуба, причем область ножки зуба проходит, если рассматривать в нормальном сечении, от окружности впадин до окружности активных точек, причем боковые поверхности профиля зубьев соседних в нормальном сечении зубьев образованы соответственно симметрично друг другу, причем ось симметрии (y) пересекает окружность впадин в нижней точке впадины,отличающееся тем, что, если смотреть в нормальном сечении, боковые поверхности профиля в области ножки зуба, начиная с релевантного диаметра (d_r), в направлении центра зубчатого колеса выполнены в форме тангенсоиды, причем тангенсоида на релевантном диаметре (d_r) переходит тангенциально непрерывно в форму боковой поверхности профиля зуба в активной области; причем тангенсоида в области ножки зуба переходит тангенциально непрерывно в дугу окружности впадины, которая касается окружности (d_f) впадин в нижней точке (FP) впадины.

2. Зубчатое колесо по п.1, отличающееся тем, что продолженная за дугу окружности впадины тангенсоида пересекает ось (y) симметрии под углом подъема 90°-γ; причем γ выбран меньше 65°.

3. Зубчатое колесо по п.1, отличающееся тем, что продолженная за дугу окружности впадины тангенсоида пересекает ось (y) симметрии под углом подъема 90°-γ; причем γ выбран меньше 50°.

4. Зубчатое колесо по п.1, отличающееся тем, что продолженная за дугу окружности впадины тангенсоида пересекает ось (y) симметрии под углом подъема 90°-γ; причем γ выбран меньше 45°.

5. Зубчатое колесо по одному из пп.2-4, отличающееся тем, что γ выбирается в зависимости от количества (z) зубьев и угла зацепления (α_r) формы боковой поверхности профиля зуба на релевантном диаметре (d_r) из зависимости 45°-180°/z-α_r.

6. Зубчатое колесо по п.5, отличающееся тем, что выбранный угол зацепления (α_r) формы боковой поверхности профиля зуба на релевантном диаметре (d_r) больше или равен 4°, в частности больше 7°.

7. Зубчатое колесо по п.1, отличающееся тем, что выбранный радиус дуги окружности впадины равен 0,1-0,6 модуля.

8. Зубчатое колесо по п.6, отличающееся тем, что выбранный радиус дуги окружности впадины равен 0,3-0,4 модуля.

9. Зубчатое колесо по п.1 или 6, отличающееся тем, что выбранный радиус дуги окружности впадины равен 0,1-0,6 ширины (S_L) впадины зуба на релевантном диаметре (d_r).

10. Зубчатое колесо по п.1 или 6, отличающееся тем, что выбранный радиус дуги окружности впадины равен 0,3-0,4 ширины (S_L) впадины зуба на релевантном диаметре (d_r).

11. Зубчатое колесо по п.1, отличающееся тем, что релевантный диаметр (d_r) меньше диаметра окружности активных точек или максимум равен ему.

12. Зубчатое колесо по п.1 или 11, отличающееся тем, что выбранный релевантный диаметр (d_r) равен среднему арифметическому между диаметром окружности активных точек и диаметром окружности выступов сопряженного колеса.

13. Зубчатое колесо по п.1, отличающееся тем, что боковая поверхность профиля зуба в активной области выполнена в виде эвольвенты.

14. Зубчатое колесо по п.13, отличающееся тем, что выбранный релевантный диаметр (d_r) больше или, по меньшей мере, равен диаметру основной окружности.