Способ определения вертикальной скорости продольных волн в слоях анизотропной среды

Способ определения вертикальной скорости продольных волн в слоях анизотропной среды

Иллюстрации

Показать все

Реферат

Изобретение относится к области сейсморазведки и может быть использовано для изучения геологического строения среды с целью обнаружения месторождений нефти, газа и других полезных ископаемых.

Скорость распространения продольной сейсмической волны в вертикальном направлении - вертикальная скорость v₀ является одним из основных акустических параметров реальной среды. Знание величины v₀ необходимо для определения структурных параметров среды и позволяет получать сведения о физических свойствах отдельных слоев. В случае изотропной среды скорость распространения сейсмической волны не зависит от направления распространения и применительно к отдельному слою называется пластовой скоростью, при этом вертикальная скорость v₀ совпадает с пластовой. Последнюю можно найти или по скважинным данным (для этого чаще всего используют акустический каротаж) или по данным метода отраженных волн, т.е. по наблюдениям на поверхности с использованием формулы Дикса (Сейсморазведка (справочник геофизика), т.2, 1990 г., М., «Недра», с.171).

Метод акустического каротажа позволяет определить вертикальные скорости для любой среды независимо от того, является ли она изотропной или анизотропной.

В то же время использование метода отраженных волн и формулы Дикса в случае анизотропной среды позволяют определять только горизонтальную скорость (v_h) и кажущуюся пластовую скорость (v_a), в слое, поскольку понятие пластовой скорости для анизотропной среды теряет физический смысл и термин пластовая скорость должен быть заменен на кажущуюся пластовую скорость (Tsvankin I., Thomsen L. Nonhyperbolic reflection moveout in anisotropic media. Geophysics, 1994, V.59, №8, p.1290-1304).

Анизотропия скоростей сейсмических волн является существенным препятствием для определения вертикальной скорости v₀ по данным метода отраженных волн. Основная проблема обусловлена тем, что кинематика отраженных волн очень слабо зависит от значений вертикальных скоростей в слоях среды (Tsvankin I., Thomsen L. Nonhyperbolic reflection moveout in anisotropic media. Geophysics, 1994, V.59, №8, p.1290-1304). Это делает практически невозможным прямое определение вертикальной скорости по данным метода отраженных волн при расстановке источников и приемников сигналов на поверхности ввиду очень слабой зависимости времени распространения сейсмической волны от величины вертикальной скорости и невозможности выделения ее на фоне помех (Tsvankin I., Thomsen L. Inversion of reflection traveltimes for transverse isotropy. Geophysics, 1995, V.60, №4, p.1095-1107).

Описан алгоритм расчета вертикальных и горизонтальных скоростей продольных волн в слабоанизотропной среде по отражениям от границ слоев, в котором для определения разности редуцированных времен отражений от границ слоя использовалось линейное (относительно параметров Томсена δ и ε) приближение (С.Н. Медведев. «Определение вертикальных и горизонтальных скоростей продольных волн в трансверсально-изотропной среде по отражениям от границ слоев». Доклады АН, 2005, т.402, №3, 393-397).

Однако ранее было показано, что эффективная лучевая скорость v_e(p) в действительности не зависит от величины вертикальной скорости v₀, а следовательно, вертикальная скорость v₀ не может быть определена по эффективной лучевой скорости (Van der Baan M., Kendall J.M. Estimating anisotropy parameters and traveltimes in the τ-p domain. Geophysics, 2002, v.67, pp.1076-1086). Таким образом, использование вместо точной (с учетом связи между разностью редуцированных времен отражений от границ слоя и скоростными параметрами слоя) зависимости эффективной лучевой скорости от скоростных параметров слоя линейное (относительно параметров Томсена δ и ε) приближение делает выводы, представленные в статье С.Н. Медведева об определения вертикальной скорости по отражениям от границ слоев несостоятельными.

Проведенный заявителем информационный поиск показал, что на сегодняшний день достоверное определение вертикальной скорости в слоях анизотропной среды возможно только при наличии скважинных данных.

Одним из скважинных методов является метод дифференциального сейсмокаротажа, при котором источник волн помещают у устья скважины, а приемник в виде зонда, состоящего, как минимум, из 2-х сейсмоприемников, закрепленных на постоянной базе, опускают в скважину (Сейсморазведка (справочник геофизика), т.1, 1990 г., М., «Недра», с.312). Способ позволяет определять пластовые (вертикальные) скорости участков разреза, пройденного скважиной, путем измерения разностей времен пробега волны между сейсмоприемниками и является наиболее близким к заявляемому.

Однако, как и любой метод сейсмокаротажа, данный способ чрезвычайно трудоемок, длителен и практически непригоден для использования в морских условиях и при изучении «тяжелых» геологических формаций.

Задача изобретения состоит в разработке способа определения вертикальной скорости продольных волн в слоях анизотропной среды по наблюдениям на поверхности.

Техническим результатом, достигаемым при осуществлении заявляемого решения, является оценка вертикальной скорости продольных волн в слоях анизотропной среды по наблюдениям на поверхности, а также значительное упрощение способа, экономичность и сокращение времени.

Поставленная задача решается способом определения вертикальной скорости продольных волн в слоях анизотропной среды путем установки источников и приемников продольных волн на исследуемой поверхности в любой системе наблюдений, возбуждение и прием отраженных волн, запись сейсмограммы, определение по полученным данным кажущейся вертикальной (v_a) и горизонтальной (v_h) скорости продольной волны в выбранном слое и последующее определение вертикальной скорости (v₀) в выбранном слое по формуле v₀=0.53 v_a+0.4 v_h.

Заявляемый метод осуществляют следующим образом. Устанавливают как источники излучения, так и приемники упругих волн на поверхности исследуемого района. В системе наблюдений общей точки приема (ОТП) или общей глубинной точки (ОГТ) или в любой другой системе наблюдений метода отраженных волн возбуждают упругую волну, принимают отраженные волны и записывают сейсмограмму. Для получения кажущейся пластовой (v_a) и горизонтальной (v_h) скорости продольной сейсмической волны в некотором выбранном слое полученные данные обрабатывают любым способом, приемлемым для используемого типа данных, а затем по найденным скоростным параметрам v_a и v_h оценивают вертикальную скорость v₀ продольной волны по формуле v₀=0.53 v_a+0.4 v_h.

Выбор источников, приемников и системы наблюдений определяется условиями ведения работ (суша, море, город), характером решаемых геологических задач (исследование глубинного строения земной коры, нефтяная, рудная, инженерная сейсморазведка) и наличием конкретного фона сейсмических помех. При морских исследованиях используют, как правило, импульсные источники возбуждения, а в качестве приемников используют сейсмоприемники давления (гидрофоны), возникающего при распространении упругой волны и преобразующегося в электрический сигнал пьезоэлектрическими преобразователями.

Способ обработки полученных методом отраженных волн данных для нахождения зависимости от глубины z кажущейся пластовой скорости v_a(z) и горизонтальной скорости v_h(z) продольных сейсмических волн может быть основан, например, на использовании двухпараметрического сембланс-анализа отражений на сейсмограмме ОГТ (т.е. при помощи двухпараметрической оптимизации с двумя неизвестными скоростными параметрами v_a и v_h), (Alkhalifan Т. Velocity analysis using nonhyperbolic moveout in transversely isotropic media. Geophysics, 1997, v.62, №6, pp.1839-1854), или при помощи двухпараметрической оптимизации по годографу отраженной волны (Grechka V., Tsvankin I. Feasibility of nonhyperbolic moveout inversion in transversely isotropic media. Geophysics, 1998, v.63, №3, pp.957-969).

Скоростные параметры v_a и v_h некоторого выбранного слоя среды можно определить также способом, основанным на использовании годографов отражений от верхней и нижней границ слоя и на свойствах эффективной лучевой скорости для этого слоя (Медведев С.Н. Глубинное сейсмическое зондирование анизотропной среды Доклады РАН, 2010, т.431, №6, 813-817).

Таким образом, заявляемый способ позволяет определить вертикальную скорость продольных волн в слоях анизотропной среды по данным наблюдений на поверхности, значительно упростить и сократить время осуществления известного способа, то есть достичь заявленного технического результата.

Заявляемый способ основан на впервые выявленной автором зависимости вертикальной скорости v₀ упругой волны в анизотропной среде от скоростных параметров v_a и v_h, которая была установлена следующим образом.

Скоростные параметры v_a и v_h анизотропной среды связаны с вертикальной скоростью v₀ известными соотношениями

v_a=v₀(1+2δ)^1/2, v_h=v₀(1+2ε)^1/2,

где δ и ε - параметры Томсена (Tomsen L. Weak elastic anisotropy. Geophysics, 1986, V.51, №10, р.1954-1966). Отсюда

v₀=v_a/(1+2δ)^-1/2, v₀=v_h/(1+2ε)^-1/2.

Реальную среду можно считать слабоанизотропной, что обеспечивает малость параметров δ и ε (Tomsen L. Weak elastic anisotropy. Geophysics, 1986, V.51, №10, р.1954-1966). Учитывая этот факт и разлагая радикалы в записанных четырех выражениях в ряд по степеням δ и ε, получим

v a = v 0 ( 1 + δ ) ,   ( 1 )

v h = v 0 ( 1 + ε ) ,   ( 2 )

v 0 = v a ( 1 − δ ) ,   ( 3 )

v 0 = v h ( 1 − ε ) ,   ( 4 )

с точностью до членов второго порядка малости относительно величин δ и ε.

Проведенный автором анализ имеющихся данных лабораторных измерений на образцах, например (Tomsen L. Weak elastic anisotropy. Geophysics, 1986, V.51, №10, p.1954-1966; Jacobsen M., and Johansen T.A. Anisotropic approximations for mudrocks: a seismic laboratory study. Geophysics, 2000, V.65, №6, р.1711-1725; Wang Z. Seismic anisotropy in sedimentary rock, part 2: Laboratory data. Geophysics, 2002, V.67, №5, р.1423-1440), показал, что в подавляющем большинстве случаев выполняются оценки δ≥-0.05, ε≤0.2. Подставив эти оценки в (3) и (4), получим

v₀≤1.05 v_a,

v₀≤0.8 v_h.

Последние соотношения определяют интервал, содержащий значения вертикальной скорости v₀, и в качестве оценки v₀ можно принять центр этого интервала, т.е. полагать

v 0 = 0 .53v a + 0 .4v h   ( 5 )

Для подтверждения полученного соотношения (5) были использованы результаты обработки экспериментальных данных вертикального сейсмического профилирования (ВСП) с использованием скважины. Используемые ниже данные ВСП включали в себя послойно найденные все три скоростных параметра v₀, v_a и v_h, вместе с параметрами δ и ε, либо только два параметра: δ и ε.

Пример данных первого типа, полученных в Северном море (Traub В., Li Xi-Y. The effects of near-surface conditions on anisotropy parameter estimations from 4C seismic data. Geophysical prospecting, 2006, V.54, p.15-28), приводится в таблице 1, где v₀* - величина вертикальной скорости, определенная по данным ВСП, a v₀ - вертикальная скорость, определенная по заявляемому способу.

Таблица 1
Номер слоя	v0*	va	vh	δ	ε	v0
1	2.2	2.26	2.43	0.03	0.11	2.17
2	2.5	2.6	2.74	0.04	0.11	2.48
3	2.55	2.7	2.86	0.06	0.13	2.57

Из этой таблицы видно, что погрешность интервальной оценки (5) вертикальной скорости v₀ не превышает 0.03 км/с.

В случае, когда результаты обработки данных ВСП приводятся не полностью (только параметры Томсена δ и ε), поступим следующим образом. Подставим выражения (1), (2) для скоростей v_a и v_h в правую часть формулы (5) и разделим результат на v₀. Тогда, обозначив через σ отношение оценки (5) вертикальной скорости к истинной величине вертикальной скорости v₀, получим

σ = 0 .53 ( 1 + δ ) + 0 .4 ( 1 + ε ) .   ( 6 )

Тогда, располагая значениями параметров δ и ε, найдем из (6) величину σ, a значит и относительную погрешность 100(σ-1) оценки (5) величины v₀ в процентах.

Нижеприведенные таблицы дают оценки отношения (6), полученные по результатам обработки данных ВСП в Мексиканском заливе (Byun B.S., Corrigan D. and Gaiser J.E. Anisotropic velocity analysis for lithology discrimination. Geophysics, 1989, 54, №12, р.15 64-1574) - таблица 2 и в северном Иране (Sadri M. and Riahi M.A. NMO correction in anisotropic media using ray velocity. Geophys. J. Int. 2009, 179, p.1781-1786) - таблица 3.

Таблица 2
Глубина (Z) км	5.33	5.42	5.51	5.6	5.69	5.78	5.91	6.0
δ	0.06	0.059	0.061	0.063	0.062	0.061	0.056	0.065
ε	0.12	0.116	0.141	0.148	0.137	0.119	0.178	0.141
σ	1.006	1.004	1.014	1.018	1.013	1.006	1.024	1.016

Таблица 3
Глубина (Z), км	0.5	1.0	1.5	2.0	2.5	3.0	3.5	4.0	4.5	5.0	5.5	6.0
δ	0.05	0.05	0.031	0.025	0.035	0.037	0.045	0.046	0.041	0.03	0.028	0.022
ε	0.15	0.126	0.1	0.079	0.062	0.06	0.068	0.062	0.057	0.057	0.06	0.062
σ	1.012	1.003	0.984	0.97	0.975	0.97	0.98	0.98	0.973	0.097	0.097	0.097

Как видно из этих таблиц, относительная погрешность 100(σ-1) оценки вертикальной скорости v₀, определенной заявляемым способом, в Мексиканском заливе изменяется от 0.4% до 2.4% (Таблица 2), а в северном Иране - от -3% до 1.2% (Таблица 3).

Рассмотренные три примера указывают на достаточно хорошую точность измерения вертикальной скорости продольных волн в анизотропной среде предлагаемым способом.

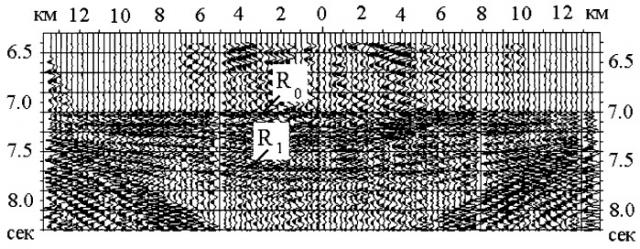
Проиллюстрируем применение предлагаемого метода измерения вертикальной скорости v₀ продольной сейсмической волны в анизотропном слое на примере обработки данных, получаемых с использованием пневмоисточника и донной сейсмической станции (OBS) в центральной котловине Японского моря.

На фиг. показан фрагмент сейсмограммы OBS, содержащий кратные отражения от морского дна (R₀) и от границы в осадочной толще (R₁) после ввода кинематических поправок

t r 2 ( X ) = t 2 ( X ) − X 2 /V 1r 2 ,   ( 7 )

где t(X) и t_r(Х) - отсчеты времен на сейсмограмме OBS, соответственно, до и после ввода кинематических поправок, Х-расстояние источник-приемник, V_1r - среднеквадратическая скорость в водной толще. Параметр V_1r подбирался так, чтобы траектория прямой (водной) волны была горизонтальна. В результате было получено значение V_1r=1.47 км/с. Это значение дает среднюю скорость звука в морской воде в районе выполнения сейсмических работ.

Определение скоростей v_a, v_h и v₀ в осадочном слое основано на использовании локального наклонного суммирования для получения годографов t₁(X) и t(X) кратных отражений, соответственно, от морского дна и от нижней границы слоя (Медведев С.Н. Определение лучевых скоростей в трансверсально-изотропной среде по сейсмограммам общего пункта приема. Геология и геофизика, 2005, т.46, №1, с.100-117). Предполагается, что границы слоя являются горизонтальными (квазигоризонтальными). Тогда t₁(X) и t(X) удовлетворяют уравнениям

t 1 2 ( X ) − T 01 2 + X 2 /V 1r 2 ,

t 2 ( X ) = T 0 2 + X 2 /V r 2 + c 4 X 4 + … ,

где T₀₁ и Т₀ - вертикальные времена кратных отражений, соответственно, от морского дна и от нижней границы слоя, V_r - среднеквадратическая скорость для двухслойной среды (водная толща плюс слой осадков), а c₄ - коэффициент негиперболичности годографа. По годографам t₁(X) и t(X) определяются параметры T₀₁ (при заданной величине V_1r), Т₀ и V_r. Знания четырех параметров T₀₁, V_1r, Т₀ и V_r достаточно (Tsvankin I., Thomsen L. Nonhyperbolic reflection moveout in anisotropic media. Geophysics, 1994, V.59, №8, p.1290-1304), чтобы найти кажущуюся пластовую скорость v_a в анизотропном слое по формуле Дикса

v a 2 = ( V r 2 T 0 − V 1r 2 T 01 ) / ( T 0 − T 01 )

Пусть p_L - наибольшая величина лучевого параметра р=dt/dX, при которой редуцированный годограф отраженной волны

τ(р,Х)=t(X)-рХ

еще имеет минимум в области прослеживания отраженной волны. Способом, изложенным в работе (Медведев С.Н. Глубинное сейсмическое зондирование анизотропной среды. Доклады РАН, 2010, т.431, №6, 813-817) по годографам t₁(X) и t(X) определим эффективную лучевую скорость v_e=v_e(p_L) в рассматриваемом слое. Тогда при заданной величине v_a найдем и горизонтальную скорость v_h в слое

v h = v a [ 1 + ( 1 − v a 2 /v e 2 ) / ( v a 2 p L 2 ) ] 1/2

При использовании изложенной здесь схемы обработки записи OBS были получены две пары скоростных параметров - для левой и правой частей сейсмограммы OBS:

v_a=1.56 км/с, v_h=1.76 км/с и v_a=1.51 км/с, v_h=1.75 км/с,

соответственно. После этого применение формулы (5) дает два соответствующих значения вертикальной скорости:

v₀=1.53 км/с и v₀=1.5 км/с.

Сравнительно небольшая величина вертикальной скорости указывает на то, что рассматриваемый слой состоит из рыхлых осадков. В пределах центральной котловины Японского моря имеется три скважины глубоководного бурения (Site 794, 795, 796). Результаты акустического каротажа, выполненного в этих трех скважинах, показывают, что вертикальная скорость продольных волн в рыхлых осадках лежит в интервале 1.5 км/с - 1.55 км/с (Tamaki К. et al. Proc. ODP. Init. Repts., 127, 1990).

Таким образом, приведенные выше значения вертикальной скорости, полученные заявляемым способом по данным метода отраженных волн с использованием донной сейсмической станции и пневмоисточника, хорошо согласуются со скважинными данными.

Способ определения вертикальной скорости продольных волн в слоях анизотропной среды путем установки источников и приемников продольных волн на исследуемой поверхности в любой системе наблюдений, возбуждение и прием отраженных волн, запись сейсмограммы, определение по полученным данным кажущейся вертикальной (v_a) и горизонтальной (v_h) скорости продольной волны в выбранном слое и последующее определение вертикальной скорости (v₀) в выбранном слое по формуле v₀=0,53 v_a+0,4 v_h.