Способ определения типа транспортных средств

Способ определения типа транспортных средств

Иллюстрации

Показать все

Реферат

Изобретение относится к области контроля движения дорожного транспорта, а именно к области опознавания транспортных средств и может использоваться, например, в в органах внутренних дел, обеспечивающих контроль дорожного движения, для определения состава транспортного потока.

В России началось поэтапное введение систем автоматической фото- и видеофиксации нарушений правил дорожного движения и администрирования штрафов в области нарушений безопасности движения. Такие системы являются эффективным средством в борьбе за безопасность дорожного движения, а также предупреждают проявления коррупции при выписывании штрафов и повышают производительность работы автоинспекции.

Одним из перспективных направлений видеофиксации нарушений представляется автоматическое распознавание типа транспортного средства (ТС) и проверка соответствия этого типа номерному знаку согласно базе данных автоинспекции.

Автоматическое определение типов ТС также полезно в целях улучшения организации транспортного движения, определения статистики загруженности дорог в зависимости от типов ТС.

Известен способ определения типа транспортных средств, в котором регистрацию сигналов от транспортных средств производят при помощи наземной обзорной радиолокационной системы, уплотняющей и излучающей обычный радиолокационный сигнал для обнаружения транспортных средств. (См. заявку на изобретение Российской Федерации №95122442, опубликована 1998 г.) В нем на ТС устанавливают ретранслятор для приема и обработки запросного сигнала радиомаяка и для излучения закодированного опознавательного сигнала.

Недостатком данного решения является невозможность использования его в дорожных условиях, так как сами ТС должны быть оснащены специальным оборудованием.

Известен также способ определения типа транспортных средств, включающий регистрацию сигналов от транспортных средств множеством датчиков, по два на каждую полосу движения (см. патент на изобретение Российской Федерации №2374693).

Этот способ выбран в качестве прототипа предложенного решения.

Недостатком данного способа также является сложность его реализации, так как требует большого количества специальных датчиков.

В предложенном изобретении ставится техническая задача упрощение способа определения типа ТС.

Данная техническая задача решается за счет того, в способе определения типа транспортных средств производят регистрацию сигналов от транспортных средств с помощью видеокамеры. Тип транспортных средств определяют с помощью трехмерной реконструкции формы транспортного средства по двумерному изображению при использовании свойства билатеральной симметрии транспортных средств.

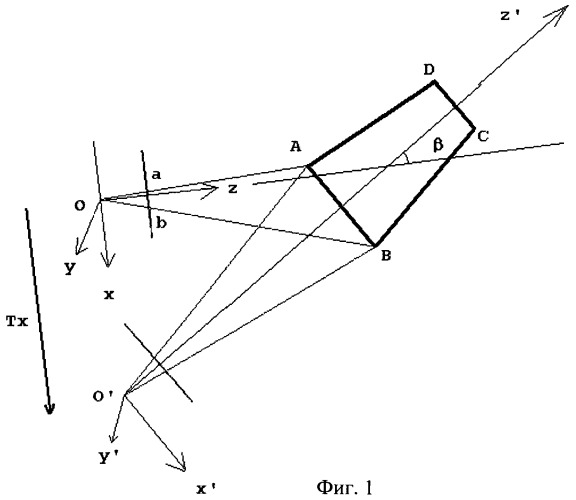
Данный способ регистрации нарушений ПДД иллюстрируется с помощью чертежей. На фиг.1 и фиг.2. показаны геометрические построения, разъясняющие способ определения типа транспортных средств.

На фиг.1. четырехугольником ABCD условно обозначено ТС. Будем считать, что ТС симметрично относительно некоторой плоскости. Например, с большой точностью внешние размеры кузова легковых автомобилей являются симметричными.

Будем считать, что объемная фигура, изображенная на фиг.1 как ABCD симметрична относительно некоторой плоскости. Задача - построить ее 3D реконструкцию.

Пусть точки A и B, симметричны относительно плоскости симметрии. В точке O расположена камера, имеющая систему координат Oxyz (см. фиг.1). Проекции трехмерных точек A и B на плоскость сенсора камеры обозначены через a и b, соответственно.

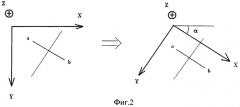
Без ограничения общности можно считать, что ось у лежит в плоскости симметрии. В противном случае всегда можно выполнить поворот на некоторый (заранее неизвестный) угол α так, чтобы ось y находилась в плоскости симметрии. Такой поворот поясняется с помощью фиг.2. Ниже показано, как определить неизвестное значение угла поворота α.

Обозначим через O' точку пересечения прямой x с плоскостью симметрии. В этой точке рассмотрим систему координат, ось y' которой совпадает с осью y, а оси x', z' получены в результате поворота на угол β вокруг оси y' так, чтобы ось z' находилась в плоскости симметрии ТС.

Координаты 3D точки в двух системах координат связаны соотношением:

X = T x + cos ( β ) * X ' − sin ( β ) * Z ' Z = sin ( β ) * X ' + cos ( β ) * Z '                           (1) Y = Y '

Пусть в системе координат O'x'y'z' точка B имеет координаты (X', Y', Z'). В силу условия симметрии точка А имеет координаты (-X', Y', Z').

В системе координат Oxyz эти точки имеют координаты (Xb, Yb, Zb) и (Xa, Ya, Za), соответственно.

Предполагая, что камера удовлетворяет принципу центральной проекции и имеет фокусное расстояние f (Д. Форсайт, Ж. Понс, Компьютерное зрение, современный подход, перевод с англ, Москва. Издательский дом Вильяме, 2004), для координат (ua, va) проекции точки А на плоскость сенсора в системе координат Oxyz и координат (ub, vb) проекции точек А и В на плоскость сенсора в той же системе координат равны:

ua=Xa*f/Za, va=Ya*f/Za

ub-Xb*f/Zb, va=Yb*f/Zb

или с учетом (I):

( u a / f ) = ( T x − cos ( β ) * X ' − sin ( β ) * Z ' ) / ( − sin ( β ) * X ' + cos ( β ) * Z ' ) ( u b / f ) = ( T x + cos ( β ) * X ' − sin ( β ) * Z ' ) / ( − sin ( β ) * X ' + cos ( β ) * Z ' ) v a / f = Y ' / ( − sin ( β ) * X ' + cos ( β ) * Z ' ) v b / f = Y ' / ( sin ( β ) * X ' + cos ( β ) * Z ' )     ( 2 )

Общее решение системы уравнений:

В системе уравнений (2) неизвестными являются координаты точки X', Y', Z', а также значение угла β поворота оси камеры к плоскости симметрии, а также вектор переноса системы координат Тх. Известными величинами являются проекции точек на плоскость камеры (ua, ub, va, vb) и фокусное расстояние f.

Перепишем (2) как:

(ua/f)*(-sin(β)*X'+cos(β)*Z')=(Тх-cos(β)*X'-sin(β)*Z')

(ub/f)*(sin(β)*X'+cos(β)*Z')=(Tx+cos(β)*X'-sin(β)*Z')

(va/f)*(-sin(β)*X'+cos(β)*Z')=Y'

(vb/f)*(sin(β)*X'+cos(β)*Z')=Y'

или

[ − ( u a / f ) * sin ( β ) + cos ( β ) ] * X ' + [ ( u a / f ) * cos ( β ) + sin ( β ) ] * Z ' = T x [ ( u b / f ) * sin ( β ) − cos ( β ) ] * X ' + [ u b / f ) * cos ( β ) + sin ( β ) ] * Z ' = T x − ( v a / f ) * sin ( β ) * X " + ( v a / f ) * cos ( β ) * Z ' = Y ' ( v b / f ) * sin ( β ) * X ' + ( v b / f ) * cos ( β ) * Z ' = Y '       ( 3 )

Откуда, исключая Tx и Y', получаем только 2 уравнения для X' и Z':

[-(ua/f)*sin(β)+cos(β)]*X'+[(ua/f)*cos(β)+sin(β)]*Z'=

[(ub/f)*sin(β)-cos(β)]*X'+[(ub/f)*cos(β)+sin(β)]*Z'

-(va/f)*sin(β)*X''+(va/f)*cos(β)*Z'=(vb/f)*sin(β)*X'+(vb/f)*cos(β)*Z'

или

[ − ( u b + u a ) * t g ( β ) + 2 f ] * X ' + ( u a − u b ) * Z ' = 0 − ( v a + v b ) * t g ( β ) * X ' + ( v a − v b ) * Z ' = 0   ( 4 )

Поскольку правая часть (4) - ноль, то нетривиальное решение для X', Z' существует только тогда, когда детерминант системы равен нулю, т.е.

[-(ub+ua)*tg(β)+2f]*(va-vb)+(va+vb)*tg(β)*(ua-ub)=0

откуда окончательно:

t g ( β ) = f ( v a − v b ) / ( u b   v a − u a   v b )   ( 5 )

Уравнение (5) можно считать аналогом соотношения Лонгета-Хиггинса для точек, снятых камерой под разными углами зрения. В данном случае такими точками являются симметричные точки.

Оставляя в (3) только три первых независимых уравнения, получим линейную систему относительно X', Y', Z'. Окончательное решение записывается в виде:

X ' / T x = ( f * ( u a − u b ) * cos [ β ] ) / D , Y ' / T x = 2 * v b * cos [ β ] ( f * cos [ β ] − u a * sin [ β ] ) / D , Z ' / T x = f * ( 2 * f * cos [ β ] − ( u a + u b ) * sin [ β ] ) / D ,   ( 6 )

где D=f*(ua+ub)*cos(2*β)+(f*f-ua*ub)*sin(2*β). Решение находится с точностью до масштабного множителя (Тх). Поэтому с точностью до масштаба можно считать Тх=1.

Если β=0 (камера смотрит прямо на объект), то из (6):

Х'/Тх=(ua-ub)/(ua+ub),

Y'/Tx=2*vb/(ua+ub),

Z'/Тх=f*2/(ua+ub).

Рассмотрим теперь вопрос о начальном повороте системы координат в плоскости сенсора. Пусть исходные координаты есть (x, y). Они связаны с координатами (u, v) соотношениями:

u = cos ( α ) * x − sin ( α ) * y v = sin ( α ) * x + cos ( α ) * y   ( 7 )

Угол α определяется из условия (5), поскольку tg(β) общий для всех точек:

( v a − v b ) / ( u b   v a − u a   v b ) = c o n s t   ( 8 )

Отсюда следует

Алгоритм определения α:

Выбираем такой угол α, чтобы для всех симметричных точек выполнялось условие (8). Для нахождения α достаточно двух пар точек, но чем больше точек - тем точнее результат.

Таким образом, зная проекции координат симметричных точек ТС на плоскость камеры, можно с точностью до масштаба восстановить трехмерные координаты точек.

В дальнейшем будем предполагать, что в результате распознавания на плоском изображении можно выделить симметричные точки, характеризующие форму кузова ТС. Такими точками могут быть, например, расстояние между фарами, нижние угловые точки лобового стекла, крайние точки бампера и т.д. С помощью рассмотренного выше алгоритма производится 3D реконструкция координат данных точек с точностью до масштаба. Отношение расстояний между данными точками характеризуют принадлежность ТС к данному классу ТС.

Таким образом, в общем случае расположении камеры достаточно выделить на изображении ТС определенное количество симметричных точек для выполнения трехмерной реконструкции и восстановление размеров ТС с точностью до масштаба.

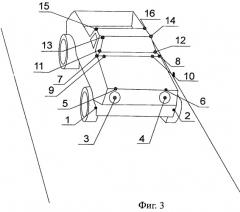
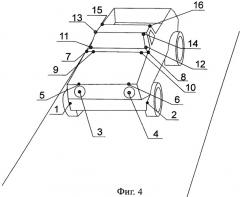
На фиг.3 показано изображение модели автомобиля. На фиг.4 приведено зеркально симметричное изображение. Специальными точками и цифрами на обоих изображениях помечены восемь зеркально симметричных точек относительно плоскости симметрии автомобиля.

На фиг.5 показана 3D реконструкция выделенных симметричных точек В следующей таблице 1 показаны контрольные измерения расстояний между точками, выполненные линейкой, в сравнении с расчетными. Расчетные расстояния нормировались на расстояние между точками 1-2, которое считалось известным. В пределах погрешностей измерений расчетные измеренные расстояния совпадают, что свидетельствует о работоспособности предложенного способа. Погрешности измерений могут быть уменьшены за счет улучшения разрешения матрицы фото- или видеокамеры, используемой для реализации способа.

Таблица 1
N п/п	Номера точек	Расстояние (в мм), вычисленное по изображениям	Расстояние (в мм), измеренное линейкой
1	3-4	57.7	58
2	5-6	62.5	63
3	7-8	87.1	85
	8-9	79.9	76
4	9-10	72.7	69
5	11-12	87.3	82

Заявленный способ определения типа транспортных средств может быть осуществлен в промышленности с применением освоенных современных технологий, материалов и процессов и может быть использован для автоматического контроля соблюдения правил дорожного движения (ПДД).

Предложенный способ определения типа транспортных средств прошел экспериментальную проверку в ООО «Вокорд СофтЛаб». Экспериментальная проверка показала упрощение определения типа транспортных средств. При этом способ показал возможность определения типа транспортных средств с помощью одной видекамеры без дополнительных датчиков. При реализации способа возможно пользоваться видеокамерами, которыми уже частично укомплектованы посты.

Предложенный способ определения типа транспортных средств рекомендован к использованию для определения типа транспортных средств органами внутренних дел и другими организациями.

1. Способ определения типа транспортных средств, включающий регистрацию сигналов от транспортных средств, при этом регистрацию сигналов производят с помощью видеокамеры, а тип транспортных средств определяют с помощью трехмерной реконструкции формы транспортного средства по двумерному изображению, отличающийся тем, что трехмерную реконструкцию формы транспортного средства по двумерному изображению проводят при использовании свойства билатеральной симметрии транспортных средств.

2. Способ по п.1, отличающийся тем, что для использования свойства билатеральной симметрии транспортных средств на двумерном изображении транспортного средства выбирают точки, которые на самом транспортном средстве являются симметрично расположенными относительно плоскости симметрии транспортного средства.

3. Способ по п.2, отличающийся тем, что в качестве симметрично расположенных точек на двумерном изображении транспортного средства выбирают одно из: точки фар, нижние угловые точки лобового стекла, крайние точки бампера.

4. Способ по любому из пп.1-3, отличающийся тем, что для построения трехмерной реконструкции формы транспортного средства используется формула (va-vb)/(ub va-ua vb)=const, (ua, va) - координаты проекции точки А на плоскость сенсора в системе координат 0xyz, (ub, vb) - координаты проекции точки В на плоскость сенсора в той же системе координат, при этом точки A и B - симметричные относительно плоскости симметрии, а в точке 0 расположена видеокамера, имеющая систему координат 0xyz, а проекции трехмерных точек A и B на плоскость сенсора видеокамеры обозначены через a и b соответственно.