Способ кодирования символа, способ декодирования символа, способ передачи символа от передатчика к приемнику, кодер, декодер и система для передачи символа от передатчика к приемнику

Способ кодирования символа, способ декодирования символа, способ передачи символа от передатчика к приемнику, кодер, декодер и система для передачи символа от передатчика к приемнику

Иллюстрации

Показать все

Реферат

Изобретение связано с областью кодирования/декодирования символа и, более конкретно, со способом кодирования символа, включающего множество значений, со способом декодирования символа, включающего множество значений и закодированного одним или более кодовыми словами, со способом передачи символа от передатчика приемнику, с компьютерной программой для выполнения способа в соответствии с изобретением, с кодирующим устройством, декодером и системой для передачи символа от передатчика приемнику. Более конкретно, осуществления изобретения относятся к новому способу энтропийного кодирования/декодирования, который основывается на кодировании по способу Хаффмана и использует многомерные кодовые слова, чтобы воспользоваться статистическими зависимостями между соседними символами и лучше приспособить длину кодового слова к вероятностям символа.

В этой области техники известны различные способы кодирования сигналов для кодирования звуковых и видео сигналов или используются для процессов кодирования в телекоммуникационной среде. Также известны соответствующие методы декодирования. Например, в области звукового кодирования ААС/МРЗ использует измененные (или расположенные друг над другом) коды Хаффмана согласно Хенке, Роберта, «Моделирование способов звукового кодирования для профессионального применения», Дипломная работа, Университет Фридриха-Александра Эрланген-Нюрнберг, Эрланген 1992, Бранденбург, Карлхайнц, Хенке, Роберта «Почти не имеющее потерь кодирование высококачественной цифровой звукозаписи: Первые результаты», ICASSP-93, ШЕЕ Международная Конференция по акустике, речи и обработке сигнала, издание 1, 27-30 апреля 1993, страницы 193-196, и ЕР 0393526 А.

Коды Хаффмана используются для кодирования квантованных спектральных коэффициентов. Спектральные коэффициенты могут быть получены из сигнала временной области посредством гребенки фильтров или преобразования. При современном состоянии звукового кодирования в качестве преобразования обычно используется MDCT (MDCT=измененное дискретное косинусное преобразование). Для квантизации обычно используется скалярный квантизатор. В случае использования кодов Хаффмана для кодирования квантованных спектральных значений, одиночные или множественные квантованные спектральные значения обозначаются как «символ». Символы, отображенные на кодах Хаффмана, ограничены в диапазоне значений наибольшим абсолютным значением (LAV), как описано Хаффманом Д.А. в работе «Способ построения кодов с минимальной избыточностью», Труды IRE (Институт радиоинженеров), сентябрь 1952, издание 40, выпуск 9, страницы 1098-1101. Например, в ААС кодировании в случае, если символ превышает LAV, символ отображается не на одиночном кодовом слове, а на последовательности двух кодовых слов. Одно из кодовых слов - так называемое «переходное кодовое слово», которое указывает на присутствие дополнительного кодового слова. Второе кодовое слово - так называемое «завершающее кодовое слово». На стороне декодера символ может быть декодирован только посредством использования всех кодовых слов из последовательности, а именно, переходное кодовое слово и завершающее кодовое слово. Завершающее кодовое слово обычно - длина серии, закодированная посредством использования измененного Кода Голомба, и показывает разницу между наибольшим абсолютным значением и значением кодированного символа. Размерность символов ограничивается максимум четырьмя, то есть, максимум четыре соседних спектральных коэффициента объединяются для одного символа. Таким образом, размерность символа указывает число значений, которые объединены в одном символе, для которого затем определяется кодовое слово для передачи декодеру. Механизм перехода используется из расчета на спектральный коэффициент, а не на символ, то есть, в случае, если один спектральный коэффициент превышает LAV, а остальные спектральные коэффициенты не превышают, механизм перехода используется только для спектрального коэффициента, превышающего LAV.

В области видео кодирования в соответствии с ITU-T спецификацией видео кодирования ITU-T H.263 (01/2005) используется комбинация одномерного кодирования по способу Хаффмана (VLC = Кодирование с переменной длиной) и механизма перехода. Этот механизм используется для кодирования квантованных DCT (DCT = дискретное косинусное преобразование) коэффициентов способом, аналогичным способу, применяемому в звуковом кодировании. В области телекоммуникаций ITU-T спецификация телефакса (ITU-T Rec. T.4 (07/2003)), описывает использование измененных кодов Хаффмана, то есть, длины серий кодируются посредством использования кодирования по способу Хаффмана. В случае, если длина серии превышает LAV, передается так называемый «добавочный код». Посредством этих добавочных кодов могут быть представлены целые кратные 64. В случае, если длины серий больше, чем 63, передается следующий меньший добавочный код. Разница с оригинальной длиной серии посылается как завершающее кодовое слово.

Вышеупомянутые описанные методы обычной технологии, основанной на кодировании по способу Хаффмана, ограничивают размерность и диапазон значений символа, чтобы сохранять требуемые объемы и конфигурации памяти низкими. Кроме того, необходимо поддерживать шифровальные книги Хаффмана или таблицы кодовых слов небольшими так, чтобы кодовые слова включали длину, которая не превышает предварительно определенного предела, чтобы передача кодовых слов могла быть выполнена в соответствии с заданными условиями. В случае, если одиночные значения превышают диапазон величин, для этих одиночных символов используется механизм перехода.

При ограничении размерности символа, длины кодового слова, обычно, не оптимальны. Для двойного кодирования по способу Хаффмана только вероятности символа р (1/2)ⁿ могут быть оптимально закодированы с использованием кодов Хаффмана, так как получающаяся длина кодового слова 1 ограничивается целым значением. Если Н(р) является энтропией символа, применяется следующее ограничение: Н(р)≤1<Н(р)+1. Отрицательные эффекты этого ограничения могут быть ослаблены посредством увеличения размерности символа до N: 1/N·Н(р)≤1<Н(р)+1/N. Однако, особенно для низких скоростей передачи данных, могут появиться многомерные символы, имеющие вероятность, больше 0.5, и для таких символов оптимальная размерность символа может быть, например, 16. Однако, 16-размерная таблица с четырьмя значениями на подсимвол нуждается в памяти для сохранения 4¹⁶=4294967296=2³² кодовых слов и длин кодового слова, которые окажут большое влияние на требуемые объемы и конфигурации памяти. Кроме того, длина кодового слова будет превышать приемлемый диапазон для многих кодовых слов.

Многосимвольные кодовые слова выгодны, если символы, подлежащие кодированию, имеют статистические зависимости. Такие статистические зависимости могут явиться результатом, например, характеристик используемого преобразования частоты и окна анализа.

Для двух статистически независимых символов условная вероятность того, что b следует за а, представляет собой Р(а|b)=Р(а)·Р{b), что приводит к оптимальной длине кода L(a|b)=L(a)+L{b), являющейся суммой оптимальных кодовых слов одиночных символов, тогда как для статистически зависимых символов условная вероятность будет другой. Например, если имеется высокая вероятность того, что символ b следует за символом а, тогда условная вероятность P(а|b)>Р(а)·Р(b) будет выше, чем для статистически независимого случая и, соответственно, оптимальная длина кода L(a|b)<L(a)+L(b) будет короче, чем сумма двух независимых оптимальных длин кодовых слов L(a) и L(b).

Чем выше размерность используемой кодовой книги, тем выше порядок зависимой вероятности Р(a|b|c|…), который может быть зарегистрирован.

Согласно осуществлению, способкодирования исходного символа, имеющего множество значений, может включать следующие шаги: (a) - определение того, может ли символ быть закодирован кодовым словом первой шифровальной книги; (b) - в случае, если символ может быть закодирован кодовым словом первой шифровальной книги, выборкодового слова, связанного с символом из первой шифровальной книги; и (c) - в случае, если символ не может быть закодирован кодовым словом первой шифровальной книги: выбор кодового слова из первой шифровальной книги, показывающий, что символ не может быть закодирован кодовым словом первой шифровальной книги;разделение символана множество первых подсимволов, каждый из первых подсимволов имеет предварительно определенное число значений исходного символа; и выборкодового слова для каждого из первых подсимволов из второй шифровальной книги, где закодированный символ, представлен одним или несколькими выбранными кодовыми словами.

Согласно другому осуществлению, способ декодирования исходного символа, имеющего множество значений и закодированный одним или более кодовыми словами, может иметь следующие шаги: (а) - определение того, может ли первое кодовое слово полностью представлять символ, используя первую шифровальную книгу; (b) - в случае, если первое кодовое слово может полностью представлять символ, используя первую шифровальную книгу, выбор символа из первой шифровальной книги, используя первое кодовое слово; и (с) - в случае, если первое кодовое слово не может полностью представлять символ, используя первую шифровальную книгу, выбор второй шифровальной книги для декодирования первых подсимволов символа, где каждый из первых подсимволов имеет предварительно определенное число значений исходного символа, и выбор записи (входа) для каждого из первых подсимволов из второй шифровальной книги, используя второе кодовое слово, где символ представлен значениями, связанными с одним или несколькимивыбранными кодовыми словами. Согласно другому осуществлению, способ передачи символа от передатчика приемнику может иметьеледующие шаги: кодирование символа первым вышеупомянутым способом; передача выбранных кодовых слов от передатчика приемнику; декодирование полученных кодовых слов согласно второму вышеупомянутому способу для получения символа; и обеспечение символа для дальнейшей обработки.

Согласно другому осуществлению, компьютерная программа для выполнения одного из вышеупомянутых способов, когда она запущена на компьютере.

Согласно другому осуществлению, кодирующее устройство может иметь вход для получения входного сигнала, имеющего символ; контур кодирующего устройства для кодирования символа из входного сигнала, где контур кодирующего устройства формируется для кодирования символа в соответствии с первым вышеупомянутым способом; и выход для обеспечения выходного сигнала, имеющего выбранные кодовые слова, представляющие символ.

Согласно другому осуществлению, декодер может иметь вход для получения входного сигнала, имеющего множество кодовых слов, представляющих символ; контур декодера для декодирования кодовых слов из входного сигнала, где контур декодера формируется, чтобы декодировать кодовые слова в соответствии со вторым вышеупомянутым способом; и выход для обеспечения выходного сигнала, имеющего символ.

Согласно другому осуществлению, система для передачи символа от передатчика приемнику может иметь вышеупомянутое кодирующее устройство; передатчик, соединенный с кодирующим устройством; канал связи, соединенный с передатчиком; приемник, соединенный с каналом связи; и вышеупомянутый декодер, соединенный с приемником.

Данное изобретение обеспечивает способ кодирования символа, включающего множество значений; способ включает:

(a) определение того, может ли символ быть закодирован кодовым словом первой шифровальной книги;

(b) в случае, если символ может быть закодирован кодовым словом первой шифровальной книги, выбор кодового слова, связанного с символом из первой шифровальной книги; и

(c) в случае, если символ не может быть закодирован кодовым словом первой шифровальной книги:

выбор кодового слова из первой шифровальной книги, показывающий, что символ не может быть закодирован кодовым словом первой шифровальной книги,

разделение символа на множество первых подсимволов, и

выбор кодового слова, по крайней мере, для одного из первых подсимволов из второй шифровальной книги.

В соответствии с первым аспектом изобретения способ кодирования включает шаг (d), в соответствии с которым для каждого первого подсимвола, который не может быть закодирован кодовым словом из второй шифровальной книги, первый подсимвол разделяется на множество вторых подсимволов, и кодовое слово выбирается, по крайней мере, для одного из вторых подсимволов из третьей шифровальной книги, где в шаге (c) кодовое слово выбирается из второй шифровальной книги для каждого из первых подсимволов, и в шаге (d) кодовое слово выбирается из второй шифровальной книги, показывая, что первый подсимвол не может быть закодирован кодовым словом второй шифровальной книги, и кодовое слово выбирается из третьей шифровальной книги для каждого из вторых подсимволов.

В соответствии со вторым аспектом изобретения в шаге (с) кодовое слово, выбранное из первой шифровальной книги, далее показывает, какой из первых подсимволов включает предварительно определенную комбинацию значений, и в шаге (с) для этих первых подсимволов, не включающих предварительно определенную комбинацию значений, кодовое слово выбирается из второй шифровальной книги.

Данное изобретение далее обеспечивает способ декодирования символа, включающего множество значений, и закодированного одним или несколькими кодовыми словами; способ, включает:

(a) определение того, может ли первое кодовое слово полностью представлять символ, используя первую шифровальную книгу;

(b) в случае, если первое кодовое слово может полностью представлять символ, используя первую шифровальную книгу, выбор символа из первой шифровальной книги, используя первое кодовое слово; и

(c) в случае, если первое кодовое слово не может полностью представлять символ, используя первую шифровальную книгу,

выбор второй шифровальной книги для декодирования первых подсимволов символа, который включает множество подсимволов, и

выбор записи (входа), по крайней мере, для одного из первых подсимволов из второй шифровальной книги, используя второе кодовое слово.

В соответствии с первым аспектом изобретения способ декодирования включает шаг (d), в соответствии с которым в случае, если вторая шифровальная книга не может полностью представлять один из первых подсимволов, третья шифровальная книга выбирается для декодирования вторых подсимволов одного первого подсимвола, который включает множество вторых подсимволов, и запись (вход) выбирается, по крайней мере, для одного из вторых подсимволов из третьей шифровальной книги, используя третье кодовое слово, где в шаге (c) первая шифровальная книга показывает для первого кодового слова, что символ не может быть декодирован из первой шифровальной книги, и для каждого из первых подсимволов запись (вход) выбирается из второй шифровальной книги, и в шаге (d) вторая шифровальная книга показывает для второго кодового слова первого подсимвола, что первый подсимвол не может быть декодирован второй шифровальной книгой, и для каждого из вторых подсимволов запись (вход) выбирается из третьей шифровальной книги.

В соответствии со вторым аспектом изобретения в шаге (c) первая шифровальная книга показывает для первого кодового слова, что символ не может быть декодирован из первой шифровальной книги, и показывает, какой из первых подсимволов включает предварительно определенную комбинацию значений, и в шаге (c) для этих подсимволов, не включающих предварительно определенную комбинацию значений, запись (вход) выбирается из второй шифровальной книги.

Осуществления данного изобретения обеспечивают гибкую, иерархическую и многомерную схему кодирования по способу Хаффмана, которая позволяет расширять размерность символа только с незначительным увеличением требования в отношении памяти. Это достигается посредством введения многомерных символов только с ограниченным диапазоном значений и (обычно) с многомерными последовательностями переключения кода. Эти механизмы перехода могут быть применены к одиночным или множественным подсимволам. Все подсимволы, которые не могут быть закодированы непосредственно, отмечаются кодом перехода, и выполняется новый шаг кодирования. Этот процесс повторяется иерархически до тех пор, пока все подсимволы не будут закодированы. Например, для следующего иерархического шага или увеличивается диапазон значений в той же самой размерности кодового слова, или уменьшается размерность кодового слова в том же самом диапазоне значений, или увеличивается диапазон значений кодового слова, и уменьшается размерность кодового слова.

Изобретательный метод более выгоден, чем традиционные методы, поскольку увеличение размерности символа обеспечивает лучшую адаптацию длины кодового слова к вероятностям символа и лучшее использование статистических зависимостей между соседними подсимволами. Кроме того, могут использоваться статистические зависимости между соседними подсимволами, которые не находятся в диапазоне значений.

Использование многомерных последовательностей переключения кода далее уменьшает требуемые объемы и конфигурации памяти для многомерных кодовых книг. Например; чтобы учесть 16-мерную шифровальную книгу, непосредственно представляющую значение 0, и значения, не являющиеся 0, через последовательность переключения кода, число кодовых слов будет 2¹⁶=65536, тогда как, наличие последовательностей переключения кода для 4 соседних символов и последующей 4-мерной кодовой книги с последовательностью переключения кода на каждый символ сократит количество (записей) входов всего до 2⁴+2⁴=16.

Если комбинация символов не может быть представлена непосредственно в многомерной кодовой книге из-за ограниченного диапазона шифровальных книг, многомерные последовательности переключения кода будут учитывать использование более низкого порядка статистических зависимостей, присутствующих в более низкоразмерных подсимволах.

Осуществления изобретения используются в области энтропийного кодирования, звукового/видео кодирования и телекоммуникаций.

Осуществления изобретения будут более детально описаны ниже со ссылкой на сопровождающие рисунки, в которых:

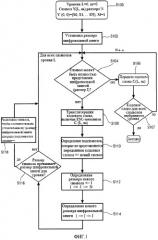
Фиг.1 - блок-схема, представляющая схему кодирующего устройства в соответствии с осуществлением изобретения;

Фиг.2 - различные таблицы кодовых слов (шифровальные книги), используемые в схеме кодирования согласно осуществлению изобретения, где фиг.2(a) является таблицей кодовых слов для 16-мерного символа (16-размерный символ = символ, состоящий из 16 значений), где фиг.2(b) является таблицей кодовых слов для 8-мерного символа, и где фиг.2(c) является таблицей кодовых слов для 4-мерного символа;

Фиг.3 - схема кодирования, использующая таблицы кодовых слов фиг.2;

Фиг.4 - схема кодирования в соответствии с дальнейшим осуществлением изобретения;

Фиг.5 - пример таблицы кодовых слов 0-ого уровня, используемой для схемы кодирования фиг.4;

Фиг.6 - блок-схема, представляющая схему декодера в соответствии с осуществлением изобретения;

Фиг.7 - схема декодирования, использующая таблицы кодовых слов фиг.2;

Фиг.8 - схема декодирования символа, закодированного согласно осуществлению фиг.6;

Фиг.9 - блок-схема примерного кодирующего устройства, использующая схему кодирования в соответствии с осуществлениями изобретения;

Фиг.10 - блок-схема примерного декодера, использующая схему декодирования в соответствии с осуществлениями изобретения; и

Фиг.11 - система для передачи символа от передатчика приемнику.

В дальнейшем, осуществления изобретения описаны, основываясь на рисунках, показывающих структурные схемы и блок-схемы. Что касается рисунков, иллюстрирующих блок-схемы устройства, отмечено, что в этих рисунках также иллюстрирован способ, где функциональные возможности блока соответствуют стадиям способа.

Фиг.1 - блок-схема, представляющая схему кодирующего устройства, работающего в соответствии с осуществлением изобретения. В шаге S100 запускается кодирование, и уровень кодирования L устанавливается на 0. Предоставляется символ Y (L, m), имеющий размер N, где размер N показывает, что символ включает N значения, a m показывает индекс подсимвола на уровне L, где m<M, и М показывает числоподсимволов для данного уровня. Подсимволы получаются посредством разделения символа Y на уровне. В шаге S100 М устанавливается на 1, и, соответствснно, m устанавливается на 0, так, чтобы символ, предоставленный в начале процесса для кодирования, был исходным символом Y(0,0)=(S₀, S₁, …, S_N).

В шаге SI02 размер шифровальной книги I устанавливается на N, то есть, шифровальная книга илитаблицакодовых слов выбирается для кодирования n-размерного символа Y.

В шаге S104 проверяется, может ли символ Y (L, m) быть полностью представлен данной шифровальной книгой, имеющей размер I. В случае, если это возможно, подходящее кодовое слово С (L, m) выбирается из шифровальной книги в шаге S106, которое может быть передано, например, декодеру, или которое может быть сохранено. В шаге S107 определяется, были ли кодовые слова выбраны для всех символов Y (L, m) на данном уровне кодирования L. В случае, если были выбраны кодовые слова для всех символов, процесс кодирования завершается и заканчивается. В противном случае, m увеличивается (m++) на один, то есть, выбирается следующий символ (подсимвол) на уровне L, и способ возвращается на шаг S104.

В случае, если символ Y (L, m) не может быть представлен кодовым словом из шифровальной книги, способ продолжается до шага S108, где кодовое слово выбирается из шифровальной книги, которая включает, по крайней мере, один механизм перехода. В шаге S110 определяется, какие подсимволы данного уровня не представлены, и эти подсимволы определяют «новый» символ. В случае, если остаются «некодированные» подсимволы, это означает, что кодирующее устройство должно использовать новую шифровальную книгу более низкой размерности, чем данная шифровальная книга. В шаге S112 определяется размер J нового символа, 1≤J≤N. В шаге S114 выбирается новая шифровальная книга, и размер I новой шифровальной книги выбирается так, чтобы он был 1≤I≤J.

В шаге S114 размер шифровальной книги может сохраняться на уровне предыдущего размера в случае, если множество подсимволов того же самого размера должно быть закодировано посредством использования, например, той же самой шифровальной книги, как ниже будет описано более детально. В таком случае в шаге S116 определяется, что размер символа не превышает размер шифровальной книги для этого уровня, и способ возвращается в шаг S104.

Альтернативно, в шаге S114 размер I новой шифровальной книги может быть выбран так, чтобы значение было меньше, чем размер J нового символа. Например, размер новой шифровальной книги может быть установлен на одну вторую размера J нового символа. В таком случае, в шаге S116 определяется, что размер J нового символа превышает размер I новой шифровальной книги так, что в шаге S118 уровень увеличивается на один (уровень ++), и символ разделяется на множество подсимволов, чтобы соответствовать размеру I шифровальной книги, выбранному в шаге S114. Кроме того, М увеличивается, показывая число подсимволов, на которое был разделен предыдущий (под-)символ. Тогда способ возвращается в шаг S104, и шаги S104 - S118 повторяются для всех подсимволов следующего уровня L так, чтобы вышеописанный иерархический процесс, в конечном счете, кодировал символ одним или несколькими кодовыми словами, которые затем могут быть переданы.

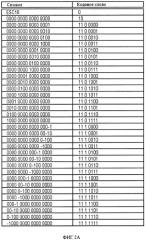
В дальнейшем, осуществление схемы кодирования описано более подробно относительно Фиг.2 и 3. Иерархическая схема включает 16-мерные, 8-мерные, 4-мерные и 1-мерные кодовые слова, которая оптимизируются для сценария, где символ 16 соседних «0» имеет вероятность 0.5. Фиг.2 показывает различные таблицы кодовых слов. Фиг.2 (а) показывает таблицу кодовых слов для 16-мерного символа. 16-мерные кодовые слова следующие:

16-мерные кодовые слова

Символ	Кодовое слово
ESC16	0
CW16: 16х, 0′	10
CW16: 15x, 0′, 1х, (+/-)1′	11 VZ XXXX

где

- VZ: знак значения (1 бит)

- ХХХХ: 4 бита для кодирования позиции значения «1» в символе

В результате получается таблица кодовых слов, показанная на фиг.2(a).

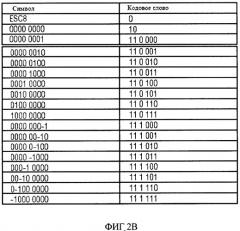
Фиг.2(b) показывает таблицу кодовых слов для 8-мерного символа, и 8-мерные кодовые слова следующие:

8-мерные кодовые слова

Символ	Кодовое слово
ESC8	0
CW8: 8х, 0′	10
CW8: 7х, 0′, 1х, (+/-)1′	11 VZ XXX

где

- VZ: знак значения (1 бит)

- XXX: 3 бита для кодирования позиции значения «1» в символе

В результате получается таблица кодовых слов, показанная на фиг.2(b).

Фиг.2(c) представляет таблицу кодовых слов для 4-мерного символа. Для 4-мерного символа S=(S₀, S₁, S₂, S₃) соответствующие кодовые слова S следующие:

- в случае, если все значения для S_n, n={0, 1, 2, 3} находятся в пределах [-1; 1], символ S=(S₀, S₁, S₂, S₃) может быть представлен непосредственно,

- в случае, если некоторые значения для S_n находятся вне пределов [-1; 1], те значения для S_n, которые находятся вне пределов [-1; 1], представлены переходными словами (ESC4), и

- в случае, если все значения для S_n находятся вне пределов [-1; 1], символ S=(S₀, S₁, S₂, S₃) представлен одиночным переходным словом (ESC4).

Например, символ S=(-1, 0, 0, -1) будет представлен непосредственно кодовым словом CW4 из таблицы кодовых слов на фиг.2 (с), символ S=(-2, 3, 4, -5) будет представлен только кодовым словом CW4=ESC4, и символ S=(-1, 3, 0, -5) будет представлен кодовым словом CW4=(-1, ESC4, 0, ESC4).

1-мерные символы, которые могут быть, в конечном счете, получены, каждый кодируется соответствующими 1-мерными кодовыми словами, которые используются, чтобы непосредственно кодировать 1-мерный символ, например, посредством кодирования длины серии.

На основе вышеописанных шифровальных книг или таблицкодовых слов будет закодирован 16-мерный символ. В шаге S100 (см. фиг.1) L устанавливается на 0, m устанавливается на 0, и N устанавливается на 16, а М устанавливается на 1. Символ, представленный в шаге S100, а именно, символ Y(0,0), включает 16 значений S₀…S₁₅. Размер шифровальной книги I устанавливается также на 16, то есть, используется таблица кодовых слов, показанная на фиг.2(a).

В шаге S104 определяется, доступна ли запись (вход) шифровальной книги для 16-мерного символа. Если дело обстоит так, соответствующее кодовое слово выбирается в шаге S106 и, например, передается так, чтобы процесс кодирования был закончен. В этой ситуации завершается процесс кодирования.

В случае, если в шаге S104 определяется, что не доступна никакая запись(вход) шифровальной книги для 16-мерного символа, в шаге S108 переходное слово выбирается и передается. Таким образом, подсимволами, еще не представленными переданными кодовыми словами, являются все 16 подсимволов, как определено в шаге S110, и размер нового символа остается равным 16, то есть, J=16 в шаге S112. В шаге S114 выбирается новая шифровальная книга, имеющая размер 8. Так как этот размер шифровальной книги меньше, чем размер нового символа J, в шаге S116 способ ответвляется на шаг S118, где 16-мерный символ подразделяется на два 8-мерных символа или подсимвола, М устанавливается на значение 2, показывающее, что теперь существуют два подсимвола, и уровень L увеличивается (уровень++) до уровня 1.

Тогда шаги S104-S118 повторяются для всех подсимволов уровня 1, то есть, для двух подсимволов, на которые исходный символ был разделен в шаге S118, а именно, два 8-мерных символа. Тогда в шаге S104 снова проверяется, могут ли оба 8-мерных символа быть непосредственно закодированы, то есть, содержится ли для каждого из них соответствующее кодовое слово в таблице кодовых слов, показанной на фиг.2(b). Если дело обстоит так, для каждого из 8-мерных символов выбирается соответствующее кодовое слово и передается в шаге S108. Тогда процесс кодирования завершается. В противном случае, то есть, в случае, если первые и/или вторые 8-мерные символы не могут быть представлены кодовым словом из 8-мерной шифровальной книги, соответствующее переходное слово выбираетсяиз шифровальной книги и передается.

Затем, в шаге S114 выбирается новая шифровальная книга, имеющая размер 4, и в шаге S118 8-мерный символ(ы), еще не закодированный, разделяется на два 4-мерных символа и повторяются шаги S104-S118. Тогда, если применимо, проверяется, могут ли 4-мерные символы быть закодированы непосредственно, то есть, содержится ли соответствующее 4-мерное кодовое слово в таблице кодовых слов, показанной на фиг.2(c). Если дело обстоит так, соответствующее кодовое слово выбирается и передается в шаге S108. В противном случае, переходное слово может передаваться или для целого 4-мерного символа или для его подсимволов. Согласно другим случаям, 4-мерный символ может быть выведен как целый символ и затем подразделен на четыре 1-мерных символа, которые кодируются в следующем шаге кодирования, используя схему кодирования, такую как описано Хенке, Робертом, «Моделирование способов звукового кодирования для профессионального применения», Дипломная работа, Университет Фридриха-Александра, Эрланген-Нюрнберг, Эрланген 1992, Бранденбург, Карлхайнц, Хенке, Роберт «Почти не имеющее потерь кодирование высококачественной цифровой звукозаписи: Первые результаты», ICASSP-93, IEEE Международная Конференция по акустике, речи и обработке сигнала, издание 1, 27-30 апреля 1993, страницы 193-196, и ЕР 0393526 А. Также могут пересылаться последовательности переключения кода на основе подсимвола, например, только для 1^-ого и 4^-ого подсимвола, тогда как 2^-ой и 3^-ий подсимвол может быть закодирован непосредственно 4-мерным кодовым словом. Процесс кодирования завершается, как только все подсимволы могут быть представлены посредством последовательности переключения кода и последовательности завершения.

Вышеупомянутое осуществление теперь будет описано более подробно на основе примера кодирования 16-мерного символа Y (0, 0)=(0, 0, 0, -1, 0, 0, 0, 0, 4, 0, -1, -5, -4, 4, 7, 5).

Уровень 0:

На уровне 0 размерность I шифровальной книги устанавливается на 16 и число подсимволов М устанавливается на 1, индекс т, соответственно, устанавливается на 0 так, чтобы Y(0, 0) имел вышеупомянутую форму, что также схематично показано цифрой 100 на фиг.3. В шаге S104 определяется, может ли символ Y(0, 0) быть полностью представлен кодовым словом из 16-мерной шифровальной книги, как показано на фиг.2(a). Как можно видеть по фиг.2(a), нет никакого соответствующего кодового слова для символа Y(0, 0), то есть, диапазон доступных кодовых слов превышен. Таким образом, выбранное кодовое слово С (0,0) является кодовым словом для последовательности переключения кода ESC16. Это кодовое слово выбирается и передается в шаге S108. Таким образом, остающиеся символы, которые не представлены кодовым словом С(0, 0), являются S₀-S₁₅.

Уровень 1:

В соответствии с шагом S112, показанным на фиг.1, теперь определяется, что размер J нового символа остается 16. Так как в шаге S108 было выбрано кодовое слово для ESC16, известно, что символ, имеющий размер J, который соответствует данному размеру, не может быть закодирован данной шифровальной книгой так, чтобы в шаге S114 была выбрана новая шифровальная книга, размером 1=8. Более конкретно, выбирается шифровальная книга или таблица кодовых слов, как показано на фиг.2(b) и, так как в шаге S116 определено, что размер J превышает размер I новой шифровальной книги, в шаге S118 уровень увеличивается до уровня 1 (уровень++), символ 100, показанный на фиг.3, разделяется на первый 8-мерный символ Y(1, 0), и второй 8-мерный символ Y(1, 1), как показано цифрами 102 и 104 на фиг.3, и М устанавливается на 2, показывая, что теперь существуют два подсимвола. Таким образом, символ был подразделен, чтобы соответствовать новому размеру I шифровальной книги:

Y(1, 0)=S₀…S₇: (0, 0, 0, -1, 0, 0, 0, 0)

Y(1,1)=S₈…S₁₅: (4, 0, -1, -5, -4, 4, 7, 5)

Шаги 104 далее повторяются для двух символов 102 и 104. Для Y (1, 0) определяется, что он может быть представлен кодовым словом из 8-мерной шифровальной книги так, чтобы соответствующее кодовое слово С(1, 0) было выбрано и передано в шаге S106, как показано на фиг.3 на уровне 1. Таким образом, выбирается кодовое слово CW8 для (0, 0, 0, -1, 0, 0, 0, 0), а именно, кодовое слово «111100».

Так как в шаге S107 определено, что не для всех символов данного уровня было выбрано кодовое слово, способ возвращается в шаг S104, и также для второго 8-мерного. символа Y(1, 1) определяется, что (4, 0, -1, -5, -4, 4, 7, 5) не может быть представлен 8-мерным кодовым словом из 8-мерной шифровальной книги, показанной на фиг.2(b). Поэтому, выбирается кодовое слово, показывающее последовательность переключения кода ESC8, а именно, кодовое слово "0", как показано на фиг.3 на уровне 1, и передается в соответствии с шагом S108, а остающиеся символы, еще не представленные кодовым словом, являются символами S₈-S₁₅, а именно, (4, 0, -1, -5, -4, 4, 7, 5).

Уровень 2:

В шаге S112 размер нового символа устанавливается на 8, то есть, соответствует числу еще не закодированных символов данного уровня. Снова, так как в шаге S108 выбирается кодовое слово для ESC8, известно, что символ, имеющий размер J, который соответствует данному размеру, не может быть закодирован данной шифровальной книгой так, что в шаге S114 выбирается новая шифровальная книга, размером I=4. Посредством шага S116 и S118 уровень увеличивается до уровня 2 (уровень++), символ 104 уровня 1, не полностью представленный кодовым словом из 8-мерной шифровальной книги, разделяется на два 4-мерных символа 106 и 108, а именно, символы Y(2, 0) и Y(2, 1), и М устанавливается на 2, показывая, что существуют два подсимвола для уровня 2. Таким образом, символ был подразделен, чтобы соответствовать новому размеру I шифровальной книги:

Y(2, 0)=S₈…S₁₁: (4, 0, -1, -5)

Y(2, 1)=S₁₂…S₁₅: (-4, 4, 7, 5)

В шаге S104 проверяется, может ли символ Y(2, 0) быть полностью представлен 4-мерной шифровально книгой фиг.2(c). Символ Y(2, 0) не может быть полностью представлен одиночным кодовым словом, однако, так как не все значения символа Y(2, 0) отличаются от 1, 0 или-1, символ Y(2, 0) представляется кодовым словом С(2, 0), которое соответствует кодовому слову, в котором символы «4», «-5» представлены последовательностью переключения кода, производящей кодовое слово CW4=(ESC4, 0, -1, ESC4). Это кодовое слово выбирается и передается в шаге S108.

В шаге S110 определяется, что для данного уровня L=2 остаются подсимволы, для которых не было выбрано никакое кодовое слово, а именно, S₁₂…S₁₅. Размер J этого нового символа - 4, то есть, соответствует данному размеру (шаг 112) так, чтобы в шаге S114 сохранялся размер шифровальной книги, и способ продолжается через шаг S116 назад, к шагу S104, без разделения нового кодового слова. Таким образом, для Y(2, 1) в шаге S104 определяется, может ли он быть представлен кодовым словом из таблицы фиг.2(c). Так как символы (-4, 4, 7, 5) не могут быть представлены 4-мерной шифровальной книгой, и так как ни одно значение этого символа не -1, 0, или 1, только последовательность переключения кода передается как кодовое слово С(2, 1)=ESC4 в шаге S108.

В шаге S110 подсимволы из уровня 2, еще не представленные кодовым словом, определяются как символы S₈, S₁₁, S₁₂, S₁₃, S₁₄, и S₁₅. В шаге S114 выбирается шифровальная книга следующего нижнего размера, 1-мерная шифровальная книга. Посредством шагов S116 и S118 остающиеся символы из уровня 2 разделяются на одиночные символы, как обозначено ссылочными знаками 110-120 на фиг.3, то есть, символ был подразделен, чтобы соответствовать новому размеру I шифровальной книги:

Y(3, 0)=S₈:(4)

Y(3, 1)=S₁₁:(-5)

Y(3, 2)=S₁₂:(-4)

Y(3, 3)=S₁₃:(4)

Y(3, 4)=S₁₄:(7)

Y(3, 5)=S₁₅:(5)

Каждый из символов Y(3, 0)-Y(3, 5) кодируется посредством использования одной из вышеописанных схем кодирования. Таким образом, теперь весь символ закодирован соответствующими кодовыми словами, которые были выбраны на различных уровнях кодирования, и эти выбранные кодовые слова могут быть объединены, что