Способ оценки дальности до точки выстрела

Способ оценки дальности до точки выстрела

Иллюстрации

Показать все

Реферат

ОБЛАСТЬ ТЕХНИКИ

Настоящее изобретение относится к техническим решениям для правоохранительных органов и служб безопасности и более конкретно к способам оценки дальности до точки выстрела. Способ обеспечивает определение и устранение неоднозначности положения точки выстрела даже для больших расстояний между точкой выстрела и датчиком, и когда отсутствует сигнал дульной волны, или этот сигнал очень слаб.

УРОВЕНЬ ТЕХНИКИ

Известны системы и способы, с помощью которых можно определить обобщенное направление и траекторию пущенного сверхзвукового объекта, например пули или артиллерийского снаряда (далее "снаряд"), измеряя параметры ударной волны, создаваемой таким пущенным объектом. Одна из таких систем, описанная в патенте США №5,241,518 содержит по меньшей мере три разнесенных датчика, каждый из которых содержит три акустических преобразователя, лежащих в некоторой плоскости. Приняв ударную волну, датчики вырабатывают сигналы, содержащие информацию, относящуюся к азимуту и углу возвышения точки возникновения ударной волны. Измерения параметров только ударной волны не позволяют определить расстояние между датчиком(ами) и точкой возникновения ударной волны. Информацию о дальности до точки выстрела обычно получают по вспышке на дульном срезе или по сигналу дульной волны.

Азимут и угол возвышения точки выстрела по отношению к положению датчика в большинстве случаев определяют, измеряя каждым датчиком время прихода дульной волны и ударной волны. Волны приходят в каждый датчик в разное время, и датчики вырабатывают сигналы, соответствующие давлению ударной и дульной волн. Обрабатывая сигналы от разных датчиков, можно определить направление (азимут и угол возвышения) от датчика на точку возникновения дульной и ударной волн и, соответственно, траекторию полета снаряда.

В известных системах используются микрофоны, которые могут быть размещены сравнительно близко друг от друга (например, на расстоянии 1 м) или же удалены друг от друга (например, могут быть смонтированы на транспортных средствах или могут носиться солдатами на поле боя), причем каждый микрофон, имеющий ненаправленную диаграмму направленности, измеряет давление дульной и ударной волн в точке его нахождения. Однако в тех случаях, когда датчики разнесены на достаточно большие расстояния, и/или траектория снаряда проходит через антенну, точность измерения времени, необходимая для точного решения задачи на основании информации только об ударной волне, должна быть очень высокой, и для ее получения требуются специальные технические средства.

Большие размеры антенны могут представлять серьезный недостаток для систем, размещаемых на транспортных средствах. Кроме того, в системах, имеющих недостаточное разрешение по времени, могут возникать неоднозначные решения, в которых времена прихода ударной волны к заданному набору датчиков почти тождественны для двух зеркально симметричных точек выстрела.

Для использования известных алгоритмов требуется по меньшей мере 4 набора данных по ударной и дульной волнам, чтобы можно было преобразовать матрицу 4×4 для отображения плоской волны по временам прихода ударной волны. Небольшие ошибки в определении времени прихода ударной и дульной волн могут приводить к существенным ошибкам в оценке дальности. Кроме того, в традиционных алгоритмах принимается предположение о постоянной скорости движения снаряда по траектории, что приводит к неточностям оценок дальностей для выстрелов с достаточно большого расстояния, более 40 м.

Соответственно, существует потребность в быстросходящихся алгоритмах, способных обеспечивать точную оценку дальности для выстрелов, сделанных с достаточно большого расстояния. Также существует потребность в устранении неоднозначности определения направления- на точку выстрела для решений, полученных на основании информации только об ударной волне. Также существует потребность в извлечении сигналов дульной волны, которые могут быть замаскированы различными акустическими сигналами, не имеющими отношения к выстрелу.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Целью изобретения является устранение недостатков технических решений предшествующего уровня, и в нем предлагается способ для оценки дальности до точки выстрела особенно для удаленных выстрелов, когда сигналы дульной волны слабы или же обнаруживаются недостаточным числом каналов обнаружения.

Предлагаемый способ также улучшает возможности устранения неоднозначности решений, получаемых на основании только информации об ударной волне, с дополнительным улучшением, достигаемьм в результате включения в процесс оптимизации слабых и/или обнаруженных с невысокой надежностью сигналов дульной волны.

В соответствии с предлагаемым способом оценки дальности до точки выстрела путем измерения ударной волны и дульной волны, измеряются сигналы, содержащие информацию только об ударной волне, а также сигналы, содержащие информацию о дульной волне. Начальная дальность до точки выстрела оценивается по измеренным сигналам ударной и дульной волны и принятым начальным значениям скорости снаряда и коэффициента его лобового сопротивления. Мгновенная скорость снаряда вдоль его траектории вычисляется итеративно для получения обновленных значений дальности до точки выстрела. Число каналов обнаружения дульной волны обычно меньше числа каналов обнаружения ударной волны.

Предпочтительные варианты осуществления изобретения могут содержать один или несколько следующих признаков. Вычисляются значения разности времени прихода между сигналами, содержащими информацию только об ударной волне, и сигналами, содержащими информацию о дульной волне, и угла прихода для определения начальной дальности до точки выстрела. Должно быть выполнено заданное количество итераций, или же обновленное значение дальности до точки выстрела будет считаться окончательной дальностью, если соотношение между последовательными обновленными значениями дальности удовлетворяет критерию сходимости. Например, критерий сходимости может быть выбран таким образом, чтобы разница между последовательными обновленными значениями дальности до точки выстрела или относительное изменение этих значений в процентах было меньше заданной величины. Для получения действительных решений вычисленная скорость снаряда ограничивается нижним предельным значением, скоростью звука. Решения проверяются на непротиворечивость. Например, обновленное значение дальности до точки выстрела считаются недействительными, если угол траектории снаряда и угол прихода, которые были определены, превышают заданное значение.

Даже если вычисленная дальность до точки выстрела признана недействительной, решение все-таки может быть получено с использованием генетического алгоритма. Например, в этом алгоритме может быть определена начальная популяция с заранее заданным числом особей, причем каждая особь представлена трехмерной строкой, которая содержит предполагаемые значения дальности до точки выстрела, углов азимута и возвышения расхождения (с направлением на систему датчиков) траектории снаряда. Генетический алгоритм выполняется для заданного числа поколений, и в каждом поколений для особей вычисляются невязки. В каждом поколении решение, имеющее наименьшее значение невязки, выбирается в качестве особи, которая остается неизмененной (без мутаций). Решение, имеющее наименьшее значение невязки, выбирается в качестве обновленного значения дальности до точки выстрела. Решение может быть уточнено выполнением для каждой трехмерной строки в поколении заданного числа итераций для вычисления уточненного значения дальности до точки выстрела, причем невязки для особей в каждом поколении вычисляются с использованием уточненного значения дальности.

Генетический алгоритм включает операторы кроссовера (скрещивания) и мутации. Оператор кроссовера осуществляет обмен азимутов расхождения и/или углов возвышения расхождения между двумя особями популяции в поколении, в то время как оператор мутации может осуществлять мутацию поля (замена значения трехмерной строки случайно выбранным значением), последовательную мутацию (введении небольшого изменения во всех полях трехмерной строки) и нулевую мутацию (особь остается неизмененной).

Другие особенности и преимущества настоящего изобретения станут ясными из нижеприведенного описания предпочтительных вариантов осуществления изобретения и из его формулы.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Эти и другие признаки и достоинства настоящего изобретения станут более понятными после детального ознакомления с описанием и прилагаемыми чертежами, на которых одинаковые элементы указаны одинаковыми ссылочными обозначениями и которые могут быть выполнены не в масштабе.

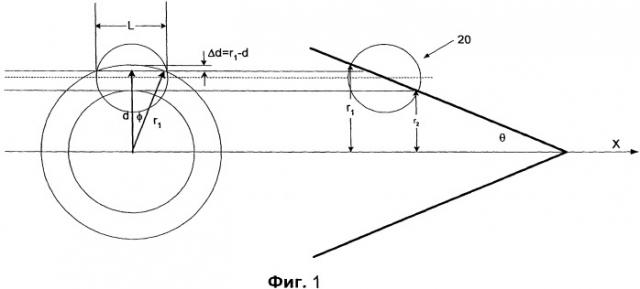
Фигура 1 - схематический вид сечения волнового конуса, пересекающегося с антенной.

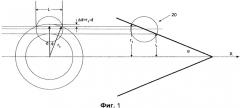
Фигура 2 - схематический вид типичной конфигурации датчиков, содержащей семь ненаправленных акустических датчиков.

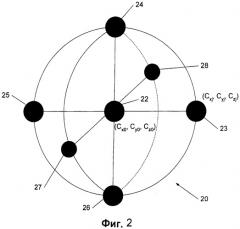
Фигура 3 - схема неоднозначности решения, присущей определению траектории на основании информации только об ударной волне.

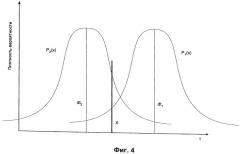
Фигура 4 - вид плотности вероятности для измерений разности времен прихода для определения окружности на поверхности волнового конуса.

Фигура 5 - график вероятности правильного разрешения неоднозначности траекторий снаряда.

Фигура 6 - блок-схема осуществления корреляционного процесса.

Фигура 7 - блок-схема генетического алгоритма, используемого для правильного разрешения неоднозначности траекторий снаряда.

Фигура 8 - блок схема алгоритма выделения сигналов, не имеющих отношения к ударной волне.

Фигура 9 - схематический вид модели времен прихода ударной волны. Фигура 10 - блок-схема алгоритма оценки дальности.

Фигура 11 - блок-схема генетического алгоритма для выполнения оценки дальности.

ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ

Как указано выше в кратком описании изобретения, предлагаются способы и системы (в различных вариантах) для оценки дальности до точки выстрела и устранения неоднозначности в определении траектории снаряда. Эти системы и способ особенно целесообразно применять в тех случаях, когда определено недостаточное количество параметров, необходимых для точного решения, или когда параметры не могут быть надежно определены.

Траектории сверхзвуковых снарядов оцениваются только по временам прихода волны, создаваемой снарядом, которые измерены несколькими близко расположенными датчиками, распределенными в "небольшом" измерительном объеме, который далее называется антенной. Измерительный объем можно считать небольшим, если расстояния между датчиками не превышают 2 метров. Как только определена траектория снаряда, становится известным и положение точки выстрела, кроме дальности до нее вдоль по траектории. Эту дальность можно найти, если антенна также измеряет время прихода дульной волны. Однако не всегда имеется возможность измерения дульной волны, так что точное решение на основе информации только об ударной волне особенно важно для определения траектории.

Как можно видеть на фигуре 1, принимается, что поверхность ударной волны представляет собой расширяющуюся коническую поверхность, ось которой совпадает с траекторией снаряда. Поверхность ударной волны также называется волновым конусом. Для того чтобы получить решение на основе информации только об ударной волне, необходимо определить по временам прихода волны, измеренным пятью или более датчиками, три величины: угол прихода волны, радиус окружности на поверхности конуса и пространственный градиент радиуса окружности на расширяющейся поверхности конуса.

Угол прихода конической поверхности, которая первой достигает антенны, определяет два возможных угла (часто называемых "неоднозначными" углами) траектории снаряда относительно угла прихода волны к антенне. "Неоднозначные" углы будут более подробно описаны ниже в связи с фигурой 3. Радиус окружности на поверхности конуса в месте нахождения антенны определяет расстояние до траектории и направление на нее. Градиент радиуса окружности вдоль генерирующей поверхности определяет направление движения снаряда, и если он известен, то это позволяет устранить неоднозначность двух возможных направлений. Точное определение этих трех величин ударной волны, требующее выполнения очень точных измерений, позволяет осуществить выбор между двумя возможными "неоднозначными" углами траектории. Например, случайные ошибки не должны превышать примерно 1 мкс для правильного выбора между двумя альтернативными углами точки выстрела.

Требуемая точность может быть определена с учетом характеристик распространения ударной волны, схема которой приведена на фигуре 1. Антенна 20, схема которой представлена на фигуре 2, содержит N датчиков (N=7), способных определять времена прихода распространяющейся конической ударной волны. Поскольку в большинстве случаев траектории снарядов могут проходить в любом направлении, то элементы 23 - 28 антенны распределяются однородно по поверхности сферы в точках С (C_xj, C_yj, C_zj), и один элемент 22 располагается в центре сферы (C_x0, C_y0, C_z0), так что антенна имеет одинаковые характеристики для любого направления прихода волны. Время обнаружения распространяющейся конической поверхности первым датчиком, назначаемым в качестве опорного, обозначено t₀. Другие датчики обнаруживают распространяющуюся коническую поверхность в последующие моменты времени, обозначенные t_j. Расстояния, которые проходит звук в направлении распространяющейся конической поверхности, получают, умножая разности времен на местную скорость звука с, то есть d_j=c·(t_j-t₀). Если ошибки измерений отсутствуют, то коническая поверхность, проходящая через опорный датчик, также определяется другими (N-1) датчиками с трехмерными координатами N точек, что обеспечивает идеальное определение всех параметров конуса ударной волны. Однако, как отмечалось выше, ошибки измерения времен прихода и координат датчиков могут приводить к определению параметров для конуса ударной волны с ошибками и, соответственно, к ошибкам определения траектории снаряда. Ниже будет рассмотрена точность определения разности времен, необходимая для правильного выбора между двумя неоднозначными углами траектории.

Система обладает особенностями, которые позволяют отбрасывать сигналы, не связанные с выстрелом, например шумы транспортного средства, вибрацию, шум ветра и электромагнитные импульсы. Например, мачта датчиков может быть установлена на транспортном средстве (не показано) с использованием эластомерных манжет в местах соединений для предотвращения дребезжания. Для крепления датчиков на окончаниях антенны могут использоваться эластомерные муфты, имеющие резонансные частоты порядка 1 Гц, для изоляции датчиков от вибрации антенны. Окончания, на которых размещаются датчики, могут быть прикреплены к общему корпусу антенны, который может содержать аналоговые электронные схемы, с помощью эластомерных амортизаторов для изоляции от вибрации мачты антенны.

Кроме того, может использоваться нижеприведенный алгоритм фильтрации сигналов, которые не обладают признаками, характерными для сигналов, связанных с ударной волной. Все величины записываются в параметрической (относительной) форме с возможностью их настройки. Указанные величины приведены лишь с целью иллюстрации.

На фигуре 8 приведена блок-схема алгоритма 800 определения связи обнаруженного сигнала с ударной волной. Алгоритм 800 начинается на стадии 802, затем на стадии 804 проверяется, достаточен ли пиковый уровень сигнала, чтобы считать его относящимся к ударной волне, например, превышает ли уровень сигнала заданное параметризованное пороговое значение, например 500. Если превышает, то выполняется стадия 806, на которой проверяется наличие резкого перехода от нулевого значения к пиковому значению сигнала, при этом проверяется также, что перед этим переходом к пиковому значению не было другого сигнала, имеющего достаточную величину, например 1/16 от пикового значения сигнала.

Если условия выполняются, то следует переход на стадию 808, на которой проверяется, что время между минимумом и максимумом ударной волны имеет достаточно большую величину, например 200-400 мкс. Если это условие выполняется, то следует переход на стадию 810, на которой проверяется, что минимальная и максимальная пиковые амплитуды сигнала достаточно близки, например первая величина составляет не меньше 35% от второй величины. Если это условие выполняется, то следует переход на стадию 812, на которой проверяется, что переход к пиковому значению давления от минимального пикового сигнала является достаточно резким; в этом случае используется тот же критерий, что и на стадии 806. Если это условие выполняется, то следует переход на стадию 814, на которой проверяется, что времена между максимальным значением сигнала и нулевым значением, и между нулевым значением и минимальным значением сигнала являются сравнимыми, например их разница находится в пределах порядка 180 мкс. Если на всех указанных стадиях получен утвердительный ответ, то принимается решение о том, что сигнал может относиться к ударной волне, и сигнал обрабатывается (стадия 816). В противном случае, если на одной из стадий алгоритма получен отрицательный ответ, то принимается решение о том, что обнаруженный сигнал не относится к ударной волне (стадия 818).

На схеме фигуры 1 принято, что траектория снаряда совпадает с осью X. Угол волнового конуса определяется выражением Θ=arcsin(1/M), где М - число Маха, определяемое как скорость V снаряда, деленная на скорость звука, с. L относится к характеристической длине антенны. Радиусы окружностей на поверхности конуса на двух концах антенны 20 равны r₁ и r₂. На схеме в левой части фигуры показано, как определяется радиус r1 окружности. Расстояние d определяется по формуле d=r₁·cos(φ). Угол (определяется по формуле sin(φ)=L/2r₁, так что для малых значений (можно принять φ~L/2r₁. Величина разности времен для окружности между точками на поверхности антенны, пересекающейся с поверхностью конуса по окружности радиуса r₁, равна dt₁=Δd/с=(r₁-d)/c~r₁·φ²/2c=L²/(8·r1·c). Величина разности времен для окружности радиуса r₂=r₁-L·sin(Θ) определяется тем же выражением, в котором r₁ заменяется на r₂. Соответственно, dt₂=dt₁+L³·sin(Θ)/8r₁ ²·с.

Принимая допущение о случайных ошибках измерения, то есть предполагая, что разности времен измерения dt₁ и dt₂ являются случайными величинами, имеющими разные средние значения, но одно и то же статистическое стандартное отклонение σ, средние величины измерений на двух концах конфигурации датчиков обеспечивают правильное определение местной окружности. Типичные распределения величин измерений для разностей времен dt₁ и dt₂ представлены на фигуре 4.

Выборочное измерение, сделанное на краю 2, обозначено X. Радиус окружности на краю 2 (радиус r₂) меньше радиуса на краю 1 (радиус r₁). Поэтому все измерения, сделанные на краю 1, которые имеют значения, превышающие X, будут приводить к правильному решению о том, что радиус окружности на краю 1 больше, чем радиус окружности на краю 2. Вероятность того, что будет принято правильное решение в случае, если измерение на краю 2 дает значение X, определяется следующим образом:

P ( r 1 < r 2 | x ) = p 2 ( x ) ∫ x ∞ p 1 ( ξ ) d ξ     ,

где p 2 ( x ) = 1 2 π ​ σ e ( x − d t 2 ) 2 2 σ 2

и p 1 ( ξ ) = 1 2 π ​ σ e ( ξ − d t 1 ) 2 2 σ 2

После интегрирования по x и подстановки переменных получается следующее выражение для вероятности принятия правильного решения:

P ( r 1 < r 2 ) = 1 2 − 1 2 π ∫ − ∞ ∞ e − u 2 e r f ( u − a ) d u

где a = d t 1 − d t 2 2 σ = L 3 s i n ( θ ) 2 8 r 1 2 c σ

На фигуре 5 приведены кривые вероятности правильного решения, или уровень доверительной вероятности для устранения неоднозначности, для двух типичных размеров антенны, L=1 м и L=2 м, в зависимости от расстояния г между ближайшей точкой траектории снаряда и антенной 20. Скорость звука с была принята равной 340 м/с. Ясно, что антенна с большими размерами имеет существенно расширенные возможности для однозначного определения точки выстрела по информации только об ударной волне. Для больших расстояний до ближайшей точки траектории разница радиусов окружностей на двух краях антенны (r₁ и r₂) слишком мала, чтобы ее можно было обнаружить, так что вероятность принятия правильного решения в этом случае достигает 50%, то есть значения полной неопределенности. Соответственно, уровень доверительной вероятности зависит от размера, а именно от диаметра антенны или ее протяженности в пространстве.

Как указывалось выше, источниками ошибок являются ошибки измерения времени и неопределенности координат датчика. Неопределенность координат датчика вносит систематические ошибки, которые существенно зависят от угла прихода ударной волны. Однако для случайно распределенных углов прихода ошибки координат датчика проявляются как случайные ошибки разностей времен.

Ошибки измерения времени определяются изменениями усиления и интенсивности сигнала от канала к каналу. Времена прихода определяют, когда выходные сигналы датчиков увеличиваются до заданного порогового значения V₀. Ошибка dt измерения времени, связанная с изменениями усиления dg, зависит от скорости нарастания напряжения в канале следующим образом:

d t = d g g V 0 d V d t

Ошибки измерения времени также возникают при изменениях уровня сигнала в пределах апертуры антенны. Для апертуры, имеющей длину L, и для цилиндрического источника звука на расстоянии r, максимальное изменение уровня сигнала в пределах апертуры равно р₀ (L/2r), где р₀ - звуковое давление по центру апертуры. Вышеприведенное уравнение для ошибки измерения времени также справедливо и для этого типа ошибки, L 2 r заменой в нем выражением d g g относительного изменения усиления

Распределение амплитудных ошибок среди датчиков не является случайным, а постепенно изменяется от максимума на краях апертуры до нуля в ее центре. На расстояниях, превышающих 10 м, и для апертуры, равной 1 м, максимальный коэффициент амплитуды не превышает 0,05, что существенно меньше параметра изменения усиления канала, равного 0,2, так что влиянием амплитудных ошибок можно пренебречь. С другой стороны, как указывалось выше, на дальностях, не превышающих 10 м, радиус волнового конуса достаточно мал по сравнению с длиной апертуры, равной 1 м, так ошибки измерений не имеют большого значения.

Практические оценки ошибок измерения времени, вызванных неопределенностью координат датчика, при допущении, что величины векторов ошибок статистически независимы и равномерно распределены между 0 и 1 мм, и что угловые ошибки статистически независимы, и стандартное отклонение имеет равномерное распределение, позволяют получить, что случайные ошибки 1 0 − 3 3 4 0 ⋅ 1 2 ⋅ т е й времен будут равны = 0,85 мкс. Стандартное отклонение для случайных ошибок дискретизации времени, имеющих биномиальное распределение, для частоты выборки 1 МГц равно 0,25 мкс. Оценка ошибок измерения времени, вызываемых изменениями усиления, дает примерно 0,75 мкс для типичной системы с шириной полосы пропускания канала, равной 18 кГц, что соответствует скорости изменения напряжения порядка 0,02 В/мкс. Используемые акустические датчики для каждой антенной системы выбирались таким образом, чтобы их чувствительности находились в пределах ±1,5 дБ. Таким образом, изменения относительного усиления каналов примерно равномерно распределены между 0,84 и 1,19, так что стандартное отклонение относительного усиления приблизительно равно

Пороговое значение напряжения V₀ равно 0,15 В, что дает величину стандартной ошибки измерения времени, равной 0,75 мкс.

Суммарные ошибки измерения времени оцениваются при допущении, что изменения усиления канала, изменения времени дискретизации и изменения положения датчиков являются статистически независимыми. В этом случае стандартное отклонение ошибки измерения времени можно оценить как √(0,85²+0,75²+0,25²)=1,1 мкс.

Такую точность трудно получить с использованием аналогово-цифрового преобразования, причем такая система будет стоить гораздо больше, поскольку в этом случае требуются высокие частоты выборки с последующей интерполяцией. В предлагаемой в изобретении системе для точного измерения разностей времен прихода используются две различные схемы.

В одном из вариантов осуществления изобретения в системе используется аналоговая схема измерения разности времен прихода, в которой в каждом канале используется тактовый генератор с частотой 1 МГц. Генераторы запускаются, когда выходной сигнал датчика превысит пороговое значение на опорном датчике, который был определен выше, как первый датчик, в который приходит ударная волна. Как указывалось выше, тактовая частота 1 МГц достаточна на практике для того, чтобы можно было пренебречь ошибками дискретизации. Система работает в аналоговом режиме, опираясь на обнаружение пороговых значений, и при этом цифровые схемы выполняют следующие функции:

1. Первый триггер устанавливается в тот момент, когда амплитуда сигнала в канале опорного датчика, то есть первого датчика, в который приходит ударная волна, достигает порогового значения.

2. Первый триггер устанавливает в нуль счетчики каналов, которые отсчитывают импульсы тактового генератора. В процессор передается предупредительный сигнал.

3. Счетчик в каждом канале работает до момента, когда в соответствующий датчик поступит ударная волна. В этом момент устанавливается второй триггер в канале, который останавливает счетчик данного канала. Если второй триггер не будет установлен, то соответствующий счетчик будет работать, пока не будет достигнуто заданное верхнее предельное значение.

4. Конечное число отсчетов в каждом счетчике запоминается в цифровом регистре разностей времен прихода.

5. Процессор считывает информацию из регистра разностей времен прихода.

6. Процессор сбрасывает счетчики для получения информации о следующей ударной волне.

В другом варианте осуществления изобретения вычисляют корреляцию для каждого канала с каждым другим каналом, для интервала времени с центром возле времени обнаружения аппаратными средствами разности времен прихода. Корреляция двух функций, обозначаемая Corr(g, h), определяется следующим образом:

C o r r ( g ,   h ) ≡ ∫ − ∞ + ∞ g ( τ + t ) h ( τ ) d τ

Корреляция является функцией, которую часто называют "временной сдвиг". Поэтому она относится к временным характеристикам, и обладает следующим свойством:

Corr(g, h)⇔G(f)H(-f)

когда g и h являются действительными функциями времени. G(f) является преобразованием Фурье g(t), a H(f) - преобразование Фурье h(t).

Суммарная энергия сигнала равна:

С у м м а р н а я     э н е р г и я   с и г н а л а = ∫ − ∞ + ∞ | h ( τ ) | 2 d τ = ∫ − ∞ + ∞ | H ( f ) | 2 d f

Сигнал времени прихода имеет конечную продолжительность, так что интегрирование (или суммирование для дискретных данных) должно быть выполнено только на ограниченном временном интервале вокруг времени прихода, причем, как это обычно используется в технике, продолжительность данных в одном или обоих каналах может быть расширена дополнением нулевыми значениями для того, чтобы продолжительности обоих сигналов были одинаковыми,

В нижеследующем рассмотрении для упрощения используются интегралы непрерывных функций, хотя реальные данные преобразованы в цифровую форму и являются дискретными. Специалисты в данной области техники легко смогут заменить интегралы суммированием.

На фигуре 6 приведена блок-схема алгоритма 60, в котором на стадиях 601, 602 в каналах i, j получают сигналы g_i(t), g_j(t), соответствующие ударной волне, и записывают их как функции от времени. На стадиях 603, 604 вычисляется суммарная энергия сигнала в канале i для последующей нормализации корреляции:

С у м м а р н а я     э н е р г и я   с и г н а л а = ∫ П р о д о л ж и т е л ь н о с т ь с и г н а л а | g i ( τ ) | 2 d τ

На стадии 605 вычисляется преобразование Фурье; временной функции g_i(t), соответствующей ударной волне, в канале i и формируется функция транспонирования G_i(-f). Аналогично, на стадии 606 вычисляется преобразование Фурье G_j(f) для временной функции g, (t) для всех других j-ых каналов. Затем на шаге 608 формируется кросс-корреляция G_i(-f)·G_j(f) для каждой пары каналов (i, j), которая является функцией "временного сдвига" t. Разность времен прихода (для каждой пары каналов является временем t_max. где f(t) имеет свою максимальную величину, стадия 610. Корреляция между каналами i и j может быть определена как

C o r r ( g i , g j ) = П и к о в о е   з н а ч е н и е   f i , j ( t ) √ ( ( Э н е р г и я   в   к а н а л е   i ) * ( Э н е р г и я   в   к а н а л е   j ) )

Невязка для канала i определяется вычислением среднего значения для датчика i по всем датчикам

Невязка (i) = Среднее ( ∑ j = i ( 1 − C o r r ( g i , g j ) ) )

как указано на стадии 612. На стадии 614 разности времен прихода и корреляции для этого канала с наилучшей (то есть с наименьшей) суммарной невязкой выбираются в качестве "лучшего" решения.

Как было указано выше, данные сигнала канала выбираются с дискретными временными интервалами на заданной частоте, например 41666,66 выборок/сек. Это соответствует ширине элемента дискретизации, равной 24 мкс, отражающей разрешение по времени для принятого сигнала. Корреляционная обработка выполняется с разрешением по времени, которое уменьшается в 8 раз до 3 мкс, то есть 333333 выборок/сек.

После того как определены разности времен прихода для всех датчиков с использованием информации только об ударной волне, могут быть определены азимут и угол возвышения точки выстрела и траектория снаряда. Положение точки выстрела, то есть ее расстояние от антенны, может быть определено, если дополнительно принят сигнал дульной волны.

В декартовой системе координат, центр которой находится в центре антенны (см. фигуру 2), то есть {(C_x0, C_y0, C_z0)=(0, 0, 0)}, время прихода ударной волны к j-ому датчику (C_xj, C_yj, C_yj) определяется выражением:

t S h o k = t 0 + L M c ( c o s ( β ) + M 2 − 1 s i n ( β ) )

где c o s ( β ) = V x ( X 0 − C x ) + V y ( X 0 − C y ) + V z ( X 0 − C z ) L M c .

V = ( V x V y V z )