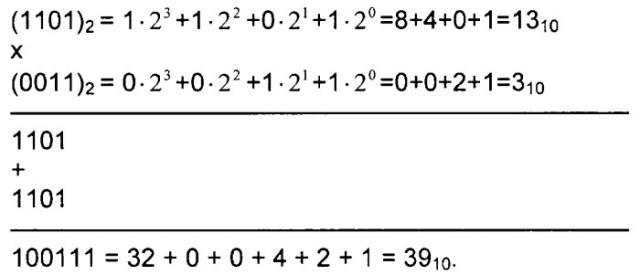Способ обработки информации и вычисления кувыркова (варианты) и устройство "генерализатор" для осуществления способа

Способ обработки информации и вычисления кувыркова (варианты) и устройство "генерализатор" для осуществления способа

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области информатики и вычислительной техники и может быть использовано в различных технологиях, требующих обработки сигналов, например в технологиях обработки и преобразования информационных сообщений.

Предлагаемое изобретение представляет собой развитие средств обработки сигналов различного характера, основанных на использовании геометрических моделей в форме графов (см. например, патент RU 2371766, опубликованный 27.10.2009). В отличие от известных решений в предлагаемом изобретении решается задача обеспечения быстродействия обработки сигнала с использованием вычислительных методов при сохранении достоверности результатов обработки. Решение подобной задачи является важным фактором, влияющим на совершенствование средств кодирования информации в системах передачи данных, при обработке внешних сигналов для выработки итогового сигнала в системах поддержки принятия решения и т.п. и может быть проиллюстрировано следующим примером.

В средствах обработки информации различного назначения используются арифметико-логические устройства, выполняющие вычисления с использованием всего многообразия существующих позиционных систем счисления, среди которых наиболее широко используются системы счисления с основанием m=2, 8, 10, 16 равным числу значений одного разряда или его алфавита (таблица 1).

Таблица 1
Системы счисления
Наименование	Основание	Алфавит
Двоичная	2	0, 1
Восьмеричная	8	0, 1, 2, 3, 4, 5, 6, 7
Десятичная	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Шестнадцатеричная	16	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Математическое выражение m-ичного числа N_m и его преобразование в десятичный вид N₁₀ определено выполнением многообразия последовательностей действий с достаточно большим числом вычислительных операций и реализации их расчетов математически представляемых суммой произведений коэффициентов i-го разряда K_i на основание позиционной системы счисления m i-ой степени mⁱ:

N m = K n − 1 ⋅ m n − 1 + K n − 2 ⋅ m n − 2 + ⋯ + K i ⋅ m j + ⋯ + K j ⋅ m j + K 0 ⋅ m 0 =         = ∑ i = 0 n − 1 K i ⋅ m i ,

где n - число разрядов, N_m - запись числа N в m-ой системе счисления, представляемого последовательностью цифр или кодом (K_n-1, K_n-2 , …, K_i, …, К₁, К₀)_m.

Например, преобразование восьмиразрядного двоичного числа, или байта (10110001)₂, в десятичное число N₁₀ осуществляется на основе выше приведенного алгоритма следующей последовательностью действий и вычислений

( 1 0 1 1 0 0 0 1 ) 2 = 1 ⋅ 2 7 + 0 ⋅ 2 6 + 1 ⋅ 2 5 + 1 ⋅ 2 4 + 0 ⋅ 2 3 + 0 ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 1 7 7 1 0 .

То есть, при данном преобразовании выполняется достаточно большое числом вычислительных операций, что очевидно усложняет вычисления и отрицательно влияет, как на быстродействие средств, обеспечивающих их выполнение, так и на надежность работы этих средств. Для решения этой проблемы вводят использование дополнительной промежуточной третьей системы вычислений.

Например, для преобразования двоичных чисел в десятичные используют дополнительно восьмеричную систему счисления, осуществляя преобразования двоичных чисел в восьмеричные и за тем уже в десятичные:

( 1 0 1 1 0 0 0 1 ) 2 = ( 2 6 1 ) 8 = 2 ⋅ 8 2 + 6 ⋅ 8 1 + 1 ⋅ 8 0 = 1 2 8 + 4 8 + 1 = 1 7 7 1 0 ,

что очевидно не решает описанную выше проблему обеспечения быстродействия и надежности вычислений.

Таким образом, при обработке сигналов с использованием вычислительных методов, предусматривающих преобразование сообщения, выраженного в одной позиционной системе счисления в другую, например двоичного числа в десятичное число, необходимо осуществить последовательность действий с достаточно большим числом вычислительных операций, которые отрицательно влияют на их быстродействие и надежность.

В свою очередь предлагаемое изобретение позволит решить указанную задачу, обеспечив как быстродействие, так и надежность при выполнении вычислений при использовании предложенного способа вычисления Кувыркова и устройства «ГЕНЕРАЛИЗАТОР» для осуществления предложенного способа.

Предложенный способ обработки информации и вычисления предусматривает параллельно-последовательную обработку сигнала, например информационного сообщения, в блоке триггеров входного регистра; матричном устройстве; блоке логических элементов, преимущественно логических элементов «И»; блоке триггеров выходного регистра. Итоговый сигнал может быть отображен на индикаторном устройстве и/или может быть использован для формирования управляющего воздействия. Обработку сигнала в матричном устройстве выполняют в соответствии с геометрической моделью обработки сигнала, представляющей собой совокупность графов, образующей, по меньшей мере, один прямоугольный треугольник. При формировании геометрической модели обработки сигнала упомянутые прямоугольные треугольники располагают в иерархическом порядке, причем к вершинам острых углов основания прямоугольного треугольника, занимающего более высокий ранг в иерархии, прилегают вершины прямых углов треугольников, занимающий более низкий ранг в иерархии. При формировании геометрической модели обработки сигнала упомянутый прямоугольный треугольник может быть разделен на три части, линиями, исходящими из вершин углов треугольника.

В итоге в матричном устройстве могут выполнять генерализацию сигнала, изначально содержащего меньшее количество разнотипных структурных элементов, в сигнал содержащий большее количество разнотипных структурных элементов, используя модель схождения от основания прямоугольного треугольника к его вершине. При этом, степень генерализации определяют через значение высоты треугольника и количество разнотипных структурных элементов в основании треугольника. В обратной ситуации в матричном устройстве могут выполнять обратную генерализацию сигнала, изначально содержащего большее количество разнотипных структурных элементов, в сигнал, содержащий меньшее количество разнотипных структурных элементов, используя модель движения от вершины прямоугольного треугольника к его основанию. В таком случае степень обратной генерализации также определяют через значение высоты треугольника и количество разнотипных структурных элементов в основании треугольника.

Наиболее предпочтительным приложением предложенного способа будет являться преобразование в матричном устройстве сообщения, выраженного в исходной позиционной системе счисления, в итоговое сообщение, выраженное в позиционной системе счисления с требуемым основанием. В таком случае количество разнотипных структурных элементов отображает количество элементов алфавита позиционной системы счисления. Подобное преобразование может быть использовано для выполнения арифметических операций, интегрирование, логические операции и т.п.

Для осуществления способа предложено вычислительное устройство, включающее последовательно соединенные блок триггеров входного регистра; матричное устройство, пересечения шин которого образуют узлы матричной решетки; блок логических элементов, преимущественно логических элементов «И»; блок триггеров выходного регистра. Пространственное расположение шин упомянутого матричного устройства соответствует расположению сторон, по меньшей мере, одного прямоугольного треугольника и выбрано исходя из геометрической модели обработки сигнала, представляющей собой совокупность графов, образующей, по меньшей мере, один прямоугольный треугольник. Прямоугольные треугольники геометрической модели обработки сигнала располагаются в иерархическом порядке, причем к вершинам острых углов основания прямоугольного треугольника, занимающего более высокий ранг в иерархии, прилегают вершины прямых углов треугольников, занимающий более низкий ранг в иерархии. В части случаев прямоугольный треугольник геометрической модели обработки сигнала может быть разделен на три части, линиями, исходящими из вершин углов треугольника.

Предложенное изобретение поясняется графическим материалом.

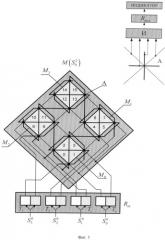
Фиг.1 - пример принципиальной схемы вычислительного устройства для преобразования числа, выраженного в двоичной системе счисления, в число, выраженное в десятеричной системе счисления.

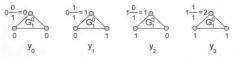
Фиг.2, 3 - пример геометрической модели для преобразования числа, выраженного в двоичной системе счисления, в число, выраженное в десятеричной системе счисления.

Предложенное вычислительное устройство (фиг.1) состоит последовательно соединенных: блока триггеров входного регистра; матричного устройства, пересечения шин которого образуют узлы матричной решетки; блока логических элементов, преимущественно логических элементов «И»; блока триггеров выходного регистра. Пространственное расположение шин упомянутого матричного устройства соответствует расположению сторон прямоугольных треугольников и выбрано исходя из геометрической модели обработки сигнала, состоящей из совокупности графов, образующих иерархический порядок из прямоугольных треугольников (фиг.2, 3). В соответствии с иерархическим порядком к вершинам острых углов основания прямоугольного треугольника более высокого ранга прилегают вершины прямых углов треугольников более низкого ранга в иерархии, соответствующей порядку выполнения вычислений. Прямоугольный треугольник геометрической модели обработки сигнала может быть разделен на три части, линиями, исходящими из вершин углов треугольника (фиг.2). Выход блока триггеров выходного регистра может быть подключен к входу индикаторного устройства или же к устройству формирования управляющего воздействия.

В соответствии со сформированной геометрической моделью обработки сигнала - совокупностью графов, образующих иерархический порядок, выполняется обработка сигнала. При этом может быть выполнена генерализация сигнала, то есть преобразование сигнала, содержащего меньшее количество разнотипных структурных элементов, в сигнал содержащий большее количество разнотипных структурных элементов, используя модель схождения от основания прямоугольного треугольника к его вершине. Либо обратный процесс - обратная генерализация (дегенерализация), то есть преобразование сигнала, изначально содержащего большее количество разнотипных структурных элементов, в сигнал, содержащий меньшее количество разнотипных структурных элементов, используя модель движения от вершины прямоугольного треугольника к его основанию. Степень генерализации и обратной генерализации определяют через значение высоты треугольника и количество разнотипных структурных элементов в основании треугольника. В случае обработки сигнала с использованием вычислительных методов, требующих преобразования позиционных систем счисления в матричном устройстве выполняется преобразование сообщения, выраженного в исходной позиционной системе счисления, в итоговое сообщение, выраженное в позиционной системе счисления с требуемым основанием. В этом случае количество разнотипных структурных элементов отображает количество элементов алфавита позиционной системы счисления. С использованием подобного преобразования может быть использовано для выполнения арифметических операций, интегрирование, логические операции и т.п.

Далее приведены примеры осуществления предложенного изобретения.

Пример обработки сигнала - информационного сообщения, предусматривающего преобразование числа, выраженного в двоичной системе счисления, в число, выраженной в десятичной системе счисления.

Геометрическая модель обработки сигнала представляет собой иерархический порядок из прямоугольных треугольников. Треугольники меньших размеров иерархически расположены в соответствии с наличием более низких уровней генерализации, каждый из треугольников может быть дополнительно разделен линиями или лучами, исходящими из его центра, на три составные части (Фиг.2, 3). В углах основания треугольников располагаются сообщения более низкого уровня генерализации, в их вершине - сообщения более высокого уровня генерализации. Соответственно ребра треугольников при схождении отображают процесс генерализации, а при обратном движении - ветвлении, отображают процесс обратной генерализации (дегенерализации).

Способ обработки сигналов выражен дробью определения значения сообщения q-го уровня генерализации

S 0 q : S ( G 0 q ) = S 0 q = S 1 q − 1 S 1 q − 1 m q = S 1 q − 1 m q + S 1 q − 1 .

Целая часть и числитель дроби представляют значения соответственно старшего S 1 q − 1 и младшего S 0 q − 1 разрядов бинарного сообщения (q-1)-го уровня генерализации, знаменатель - значение меры q-го уровня генерализации m_q, изменяющейся при переходе от одного ее уровня к другому. Мера генерализации m q = 2 h определена значением высоты треугольника h = 1 2 n 0 и числом разрядов сообщения нулевого уровня генерализации в его основании n₀. Для треугольника первого уровня генерализации G 0 1 в его основании расположены элементы сообщения нулевого уровня генерализации, или двоичные сообщения в виде совокупности разрядов двоичного числа, а в его вершине числовое значение результата вычислений в десятичном виде, или десятичное число S 0 1 . На первом уровне генерализации выполняются следующие вычисления:

S 1 ( G 0 1 ) = S 1 1 = S 3 0 S 2 0 m 1 = S 3 0 ⋅ m 1 + S 2 0 , S 0 ( G 0 1 ) = S 0 1 = S 1 0 S 0 0 m 1 = S 1 0 m 1 + S 0 0 ,

например, при S 1 0 = 1 и S 0 0 = 0, представляющие собой двоичное число (10)₂, имеет десятичное значение равное 2

S 0 ( G 0 1 ) = S 1 0 S 0 0 m 1 = 1 0 2 = 2 .

В итоге в вершине иерархического порядка треугольников получают итоговое значение, выраженное соответствующей дробью.

Входной регистр вычислительного устройства содержит блок триггеров, соединенных своими выходами со входами шин матричного устройства, на пересечениях которых в узлах решетки расположены соединенные с ними своими входами логические элементы типа "И". С выходов логических элементов результаты генерализации входной информации в десятичном виде поступают в выходной регистр и далее на сумматор и индикатор их визуального представления. Направления пространственного расположения шин матрицы вычислительного устройства определены направлениями пространственного расположения сторон или ребер прямоугольного треугольника геометрической модели, исходящих из его вершины S 0 q к углам S 0 q − 1 и S 1 q − 1 . Направления пространственного расположения сторон к углам S 0 q − 1 и S 1 q − 1 определяют соответственно нулевой и единичный признаки пространственного направления шин матрицы: нулевой признак шин определен их параллельностью стороне треугольника S 0 q S 0 q − 1 , единичный - S 0 q S 1 q − 1 .

При подаче на вход вычислительного устройства исходного сообщения, например, четырех разрядного двоичного числа или двоичного сообщения n₀=4, результаты процесса генерализации будут рассредоточены по узлам решетки его матрицы, на пересечениях шин нулевого и единичного признаков с общим числом узлов, а следовательно и результатов расчетов, равным 2⁴=16. В случае преобразования двоичной системы счисления выходы триггеров входного регистра генерализатора будут соединены со входами шин его матричного устройства следующим образом: нулевые выходы триггеров Т₀ и T₁ соединены соответственно со входами шин нулевого и единичного признаков с четными порядковыми номерами, единичные выходы триггеров Т₀ и T₁ соединены соответственно со входами шин нулевого и единичного признаков с нечетными порядковыми номерами; нулевые выходы триггеров Т₂ и Т₃ соединены соответственно со входами общих шин нулевого и единичного признаков нулевого и первого порядковых номеров, первые выходы триггеров Т₂ и Т₃ соединены соответственно со входами общих шин нулевого и единичного признаков второго и третьего порядковых номеров.

Пример обработки сигнала - информационного сообщения, предусматривающего сложение двоичных чисел x₁+х₂.

Сложение двоичных чисел: x₁+x₂, например, при x₁=(1101)₂; x₂=(0011)₂. Используя известные методики, сложение двоичных чисел с последующим их преобразованием в десятичный вид содержит множество тактов и процессов вычислений:

( 1 1 0 1 ) 2 = 1 ⋅ 2 3 + 1 ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 8 + 4 + 0 + 1 = 1 3 1 0 + ( 0 0 1 1 ) 2 = 0 ⋅ 2 3 + 0 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 0 + 0 + 2 + 1 = 3 1 0 ( 1 0 0 0 0 ) 2 = 1 ⋅ 2 4 + 0 ⋅ 2 3 + 0 ⋅ 2 2 + 0 ⋅ 2 1 + 0 ⋅ 2 0 = 1 6 + 0 + 0 + 0 + 0 = 1 6 1 0 .

В соответствии с предложенным способом результаты вычисления получают непосредственно в десятичном виде, осуществляя поразрядное десятичное сложение их составляющих с последующим преобразованием в соответствии с предложенным способом в десятичный вид при параллельности вычислений и значительно меньшем числе их тактов и вычислительных операций:

1 1 0 1 + 0 0 1 1 _ 1 1 1 2

Пример обработки сигнала - информационного сообщения, предусматривающего сложение и вычитание двоичных чисел x₁+x₂-x₃.

Сложение и вычитание двоичных чисел x₁+x₂-x₃, например x₁=(0101)₂; x₂=(1000)₂; x₃=(0110)₂.

Используя известные методики, сложение и вычитание двоичных чисел с последующим их преобразованием в десятичный вид содержит множество тактов и вычислительных операций:

( 0 1 0 1 ) 2 = 0 ⋅ 2 3 + 1 ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 0 + 4 + 0 + 1 = 5 1 0 + ( 1 0 0 0 ) 2 = 1 ⋅ 2 3 + 0 ⋅ 2 2 + 0 ⋅ 2 1 + 0 ⋅ 2 0 = 8 + 0 + 0 + 0 = 8 1 0 − ( 0 1 1 0 ) 2 = 0 ⋅ 2 3 + 1 ⋅ 2 2 + 1 ⋅ 2 1 + 0 ⋅ 2 0 = 0 + 4 + 2 + 1 = 6 1 0

( 0 1 1 1 ) 2 = 0 ⋅ 2 3 + 1 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 0 + 4 + 2 + 1 = 7 1 0 .

В соответствии с предложенным способом результаты вычислений сложения и вычитания двоичных чисел получают непосредственно в десятичном виде, осуществляя поразрядное десятичное сложение и вычитание их составляющих с последующим преобразованием в соответствии с предложенным способом в десятичный вид при параллельности вычислений и значительно меньшем числе их тактов и вычислительных операций:

Пример обработки сигнала - информационного сообщения, предусматривающего умножение двоичных чисел x₁·x₂.

Умножение двоичных чисел x₁·x₂, например, при x₁=(1101)₂; x₂=(0011)₂.

Используя известные методики, осуществим последовательное поразрядное умножение составляющих данных чисел с последующим преобразованием результата в десятичный вид при последовательном выполнении множества тактов и вычислительных операций:

Используя предложенный способ, вычисление произведения двоичных чисел осуществим непосредственно в десятичном виде в следующей последовательности (см. таблицу 2):

1) в соответствии с предложенным способом преобразуем любое из заданных двоичное число в десятичный вид при параллельности выполняемых при этом вычислений,

2) полученный результат умножаем поразрядно на составляющие другого двоичного числа,

3) полученный результат от умножения, используя предложенный способ, преобразуем в десятичный вид, используя при этом параллельность вычислений и меньшее число тактов и вычислительных операций.

Таблица 2
	(1)
1 1 0 1 × 3 3 3 0 3	(2)
	(3)

Пример обработки сигнала - информационного сообщения, предусматривающего деление двоичных чисел x₁:x₂.

Деление двоичных чисел х₁·x₂, например, при x₁=(1100)₂; Х₂=(0011)₂.

Используя предложенный способ, вычисление деления двоичных чисел осуществим непосредственно в десятичном виде в следующей последовательности (см. таблицу 3):

1) в соответствии с предложенным способом преобразуем любое из заданных двоичное число в десятичный вид при параллельности выполняемых при этом вычислений,

2) на полученный результат делим поразрядно составляющие другого двоичного числа,

3) полученный результат от деления, используя предложенный способ, преобразуем в десятичный вид, используя при этом параллельность вычислений и меньшее число тактов и вычислительных операций.

Таблица 3
	(1)
1 1 0 0 : 3 1 3 1 3 0 0	(2)
	(3)

Пример обработки сигнала - информационного сообщения, предусматривающего интегрирование.

Интегрирование: определение суммы значений функции, представляемых на заданном интервале изменения ее аргумента, например, y(х₀)=0; y(x₁)=2; y(х₂)=1; y(х₃)=4; y(х₄)=5; y(х₅)=2; y(x₆)=3; y(х₇)=2.

Используя известные методики, осуществим сложение значений функции, представленных двоичными числами с последующим их преобразованием в десятичный вид:

В свою очередь, используя предложенный способ, результаты вычислении интеграла функции y(х) осуществим непосредственно в десятичном виде, используя значительно меньшее число тактов и вычислительных операций:

0 0 0 0 + 0 0 1 0 + 0 0 0 1 + 0 1 0 0 + 0 1 0 1 + 0 0 1 0 + 0 0 1 1 + 0 0 1 0 0 2 4 3

Пример обработки сигнала - информационного сообщения, предусматривающего логическое суммирование.

Логическое суммирование, например,

y₀=x₀ ∨ х₀=0 ∨ 0=0;

y₁=х₀ ∨ x₁=0 ∨ 1=1;

y₂=x₁ ∨ x₀=1 ∨ 0=1;

y₃=x₁ ∨ x₁=1 ∨ 1=2.

Для получения данных результатов, из-за несоответствия арифметических и логических вычислений, исключительно благодаря универсальности предложенного способа его можно использовать не только для арифметических, но и логических вычислений:

Таким образом, с помощью предложенного способа обработки информации и вычисления можно осуществить решение всех известных задач, предусматривающих использование арифметических и логических вычислений. Приведенные примеры практического использования подтверждают его достоинства и перспективы широкого применения для новых поколений ЭВМ и информационной техники, обеспечивая повышение универсальности, простоты, надежности и быстродействия.

1. Способ обработки информации и вычисления, предусматривающий параллельно-последовательную обработку сигнала вблоке триггеров входного регистра; матричном устройстве; блоке логических элементов, преимущественно логических элементов «И»; блоке триггеров выходного регистра;причем обработку сигнала в матричном устройстве выполняют в соответствии с геометрической моделью обработки сигнала, представляющей собой совокупность графов, образующей, по меньшей мере, один прямоугольный треугольник,а упомянутый прямоугольный треугольник разделяют на три части линиями, исходящими из вершин углов треугольника.

2. Способ по п.1, отличающийся тем, что при формировании геометрической модели обработки сигнала упомянутые прямоугольные треугольники располагают в иерархическом порядке, причем к вершинам острых углов основания прямоугольного треугольника, занимающего более высокий ранг в иерархии, прилегают вершины прямых углов треугольников, занимающий более низкий ранг в иерархии.

3. Способ по п.1, отличающийся тем, что в матричном устройстве выполняют генерализацию - преобразование сигнала, изначально содержащего меньшее количество разнотипных структурных элементов, в сигнал, содержащий большее количество разнотипных структурных элементов, используя модель схождения от основания прямоугольного треугольника к его вершине.

4. Способ по п.3, отличающийся тем, что степень преобразования - генерализации определяют через значение высоты треугольника и количество разнотипных структурных элементов в основании треугольника.

5. Способ по п.1, отличающийся тем, что в матричном устройстве выполняют обратную генерализацию - преобразование сигнала, изначально содержащего большее количество разнотипных структурных элементов, в сигнал, содержащий меньшее количество разнотипных структурных элементов, используя модель движения от вершины прямоугольного треугольника к его основанию.

6. Способ по п.5, отличающийся тем, что степень преобразования - обратной генерализации определяют через значение высоты треугольника и количество разнотипных структурных элементов в основании треугольника.

7. Способ обработки информации и вычисления, предусматривающий параллельно-последовательную обработку сигнала вблоке триггеров входного регистра; матричном устройстве; блоке логических элементов, преимущественно логических элементов «И»; блоке триггеров выходного регистра;причем обработку сигнала в матричном устройстве выполняют в соответствии с геометрической моделью обработки сигнала, представляющей собой совокупность графов, образующей, по меньшей мере, один прямоугольный треугольник, в ходе которойвыполняют интегрирование с использованием преобразования сообщения, выраженного в исходной позиционной системе счисления, в итоговое сообщение, выраженное в позиционной системе счисления с требуемым основанием, причем количество разнотипных структурных элементов отображает количество элементов алфавита позиционной системы счисления.

8. Способ по п.7, отличающийся тем, что при формировании геометрической модели обработки сигнала упомянутые прямоугольные треугольники располагают в иерархическом порядке, причем к вершинам острых у