Усовершенствованное кодирование/декодирование цифровых сигналов, в частности, при векторном квантовании с перестановочными кодами

Усовершенствованное кодирование/декодирование цифровых сигналов, в частности, при векторном квантовании с перестановочными кодами

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Настоящее изобретение относится к кодированию/декодированию цифровых сигналов, таких как аудиосигналы, видеосигналы, и в целом мультимедийные сигналы, с целью их записи или их передачи. В частности, изобретением предлагается решение проблем, возникающих при кодировании и декодировании перестановочных кодов.

Обычно изобретение применяется также к дуальной схеме кодирования источника: канального кодирования или «модуляции».

Кодирование/декодирование со сжатием цифровых сигналов в рамках настоящего изобретения может быть использовано для квантования коэффициентов трансформанты частотных кодеров речевых сигналов и/или аудиосигналов.

Уровень техники

Векторное квантование

Очень распространенным решением при сжатии цифровых сигналов является векторное квантование. Векторное квантование представляет входной вектор в виде вектора одинакового размера, выбранного из конечного множества. Квантор на М уровней (или «векторов-кодов») является примером не биективного применения множества входных векторов, как правило, реального евклидового n-размерного пространства Rⁿ или подмножества Rⁿ в конечном подмножестве Y Rⁿ с М отдельных элементов: Y={y₀, y₁, …, y_m-1}.

Y называют алфавитом воспроизведения или «словарем» или «справочником», а его элементы векторов-кодов - «кодовыми словами» (или «выходными точками» или «репрезентантами»).

Пропускная способность по размеру r квантора (или его «разрешение») определяют.отношением:

При векторном квантовании блок из n выборочных значений обрабатывают как вектор размера n.Согласно теории кодирования источника, когда размер становится очень большим, эффективность векторного квантования приближается к границе пропускная способность - искажение источника. Словари векторных кванторов могут быть разработаны на основании статистических методов, таких как обобщенный алгоритм Ллойда (или "GLA" от "Generalized Lloyd Algorithm"), основанный на необходимых условиях оптимальности векторного квантора. Полученные таким образом статистические векторные кванторы не имеют никакой структуры, что делает их просмотр сложным и дорогим с точки зрения вычислительных или записывающих ресурсов, поскольку сложность как при кодировании, так и при записи прямо пропорциональна: n2^nr.

Показанный на фиг.1А векторный квантор используют для трех основных операций: двух при кодировании и одной при декодировании. Входной вектор кодируют (этап COD), выбирая сначала вектор-код из словаря. Речь идет о наиболее «похожем» на него векторе-коде (операция ОР1 на фиг.1А). Затем, определяют индекс этого вектора-кода (этап IND) для передачи или введения в память (операция ОР2 на фиг.1А). На декодере (этап DEC) вектор-код определяется по его индексу (операция ОР3 на фиг.1А).

При модуляции тоже используют три операции ОР1, ОР2 и ОР3, показанные на фиг.1А, но в другом порядке. Согласно фиг.1В, которая иллюстрирует эту дуальность модуляция/квантование, предусматривают переход от индекса к вектору-коду (этап COD' на фиг.1В, соответствующий операции ОР3 на фиг.1А). Затем после передачи на зашумленном канале выявляют вектор-код, наиболее близкий к полученному вектору (этап DEC на фиг.1В, соответствующий операции ОР1 на фиг.1А). Наконец, на третьем этапе (этап IND' на фиг.1В, соответствующий операции ОР2 на фиг.1А) производят декодирование индекса вектора-кода.

Экспоненциальное возрастание сложности в зависимости от размера векторов и от пропускной спосоюности ограничивает применение не структурированных векторных кванторов при небольших размерах и/или низкой пропускной способности для их использования в реальном времени. В случае не структурированного векторного квантора поиск наиболее близкого вектора-кода (операция ОР1) требует исчерпывающего поиска среди всех элементов словаря для выбора элемента словаря, который минимизирует измерение расстояния между ним и входным вектором. Две последние операции (индексация ОР2 и обратная операция ОР3) обычно осуществляют путем простого считывания таблиц, но они все равно занимают много места в объеме памяти. Чтобы устранить проблемы размера и расстояния, были изучены многие варианты базового векторного квантования. Они призваны решить проблему отсутствия структурности словаря и помогают снизить сложность, но в ущерб качеству. И все-таки компромисс эффективность/сложность был улучшен, что позволяет расширить диапазон разрешений и/или размеров, в котором можно эффективно применять векторное квантование с точки зрения стоимости. Было предложено много схем структурированных векторных кванторов и, в частности, векторный квантор, использующий описанный ниже «перестановочный код».

Перестановочные коды

В векторном кванторе с «перестановочным кодом» векторы-коды получают путем перестановок компонент первого вектора-кода (в смысле лексикографического порядка), называемого «лидером» (или «вектором-директором»). Эти компоненты принимают свои значения в алфавите А={a₀, a₁, a_q-1} размером q (алфавита А q-площадь, где a_i≠a_j при i≠j). Компоненты a_i являются вещественными (или целыми) числами. Весовой коэффициент wⁱ (где i является индексом от 0 до q-1) является числом повторений буквы a₁ алфавита. Весовые коэффициенты wⁱ являются положительными целыми числами, такими, при которых ∑ i = 0 q − 1 w i = n Условно значения алфавита удовлетворяют a₀>a₁> … >a_q-1. n компонент лидера уменьшаются от позиции 0 до позиции (n-1). Таким образом, вектор-лидер у₀ является вектором размера n, имеющим форму:

Понятно, что можно выбрать другой порядок компонент, например a₀<a₁<…<a_q-1.

Вектор-лидер называют «лидером со знаком», и перестановочный код называют «типа I». Путем перестановок компонент y₀ получают другие векторы-коды. Общее число М перестановок равно:

Существует другой тип перестановочного кода (тип II). Вектор-лидер имеет ту же форму, что и в предыдущем случае, но его компоненты должны быть положительными (a₀>a₁>…>a_q-1≥0). Путем перестановок компонент y₀ получают также другие векторы-коды, присваивая им все возможные комбинации знаков. Общее число М перестановок равно:

где h=n, если a_q-1>0, и h=n-w^q-1 в остальных случаях.

В этом случае вектор-лидер называют абсолютным лидером.

Векторный квантор с «перестановочным кодом» был распространен на состав (или объединение) перестановочных кодов, и недавно эта структура с объединением перестановочных кодов была общепринята для векторного квантования с переменными размером и разрешением (в документе WO-04/00219 на имя заявителя). Перестановочные коды используют не только при статистическом векторном квантовании. Они находят свое применение также при алгебраическом векторном квантовании, для которого используют сильно структурированные словари, получаемые из правильных сетей точек или из кодов корректировки погрешностей. Эти перестановочные коды применяют также при модуляции.

Использование структуры с перестановочным кодом позволяет разрабатывать оптимальные и быстрые алгоритмы поиска наиболее близкого вектора-кода (операция ОР1 на фиг.1А). Вместе с тем индексация (или нумерация) векторов-кодов (операция ОР2 на фиг.1А) и обратная операция декодирования (операция ОР3 на фиг.1А) требуют большего числа вычислений, чем в случае не структурированных векторных квантований.

Существует несколько способов нумерации перестановок. Одним из таких способов является алгоритм Шальквийка: "An algorithm for source coding" Schalkwijk J.P.M., в ГЕЕЕ Trans, on information Theory, том IT-18, №3, стр.396-399, май 1972.

Используя комбинаторный анализ, эти способы позволяют индексировать вектор-код перестановочного кода (операция ОР2), а также осуществлять обратную операцию декодирования индекса (операция ОР3). Среди алгоритмов индексации перестановок следует еще раз упомянуть алгоритм Шальквийка, широко используемый в стандартах:

- [3GPP TS 26.273] (ANSI-C code for the Fixed-point Extended AMR-Wideband (AMR-WB+) cjdec; V6.1.0 (2005-06) (Release 6)), и

- [3GPP TS 26.304] (Extended Adaptive Multi-Rate - Windeband (AMR-WB+) codec; Floating-point ANSI-C code; V6.3.0 (2005-06) (Release 6), июнь 2005).

Вычисление ранга перестановки при кодировании (операция ОР2 на фиг.1)

Ставится задача упорядочения и индексации всех возможных перестановок компонент вектора y=(y₀, y₁, …, y_n-1). Порядок является лексикографическим, и в данном случае индекс называют «рангом». Вычисление ранга вектора у приводит к вычислению вектора D=(d₀, d₁, …, d_n-1), связанного с у и такого, что d_k соответствует значению индекса d, если и только если У_k=a_d.

Например, вектор у размером n=8 имеет следующие компоненты:

Y=(4, 2, 4, 0, 0, 4, 4, 2)

Алфавит из q=3 букв (компоненты разных значений) вытекает из А={4, 2, 0} при a₀=4, a₁=2 и a₂=0.

При этом с вектором y связывают вектор D=(0, 1, 0, 2, 2, 0, 0, 1), компоненты которого являются просто индексами q букв алфавита А.

Ранги y и D являются идентичными, но определение вектора D позволяет ограничиться вычислением ранга последовательности D со значениями в множестве {0, 1, q-1} (содержащем то же число элементов, что и алфавит {a₀, a₁, …, a_q-1}).

Весовые коэффициенты векторов y и D являются идентичными, поскольку вхождения их соответствующих компонент являются идентичными. Определяют также промежуточный весовой коэффициент как весовой коэффициент вектора с компонентами (y_k, y_k+1, …, y_n-1), который, таким образом, соответствует усеченному вектору y, оставляя позиции от k до n-1. Таким образом:

где δ(x,y) является оператором Кронекера (δ(x,y)=1, если x=y и 0, если нет).

Получаем: ( w 0 0 , w 0 1 , … , w 0 q − 1 ) = ( w 0 , w 1 , … , w q − 1 ) .

При комбинаторном анализе ранг t вектора y можно вычислить при помощи следующей формулы:

Эту формулу можно упростить до:

Именно эту последнюю формулу используют чаще всего, и ее мы будет применят в данном случае. В дальнейшем будет называться «частичным рангом порядка k», при:

Декодирование ранга (операция ОР3): Определение перестановки по ее индексу Декодирование ранга t состоит в нахождении вектора D=(d₀, d₁, …, d_n-1), связанного с y. Метод последовательного поиска значений d_k описан ниже. Сначала определяют компоненту d₀, затем компоненту d₁, … до компоненты d_n-1.

* Определение d₀:

Чтобы найти d₀, используют формулу, содержащую неравенства:

Члены (n-1)!, t, и значения при d=0, …, q-1 известны.

Чтобы найти значение d₀, исходят из того, что d₀=0, осуществляют последовательную инкрементацию d₀ на 1 до тех пор, пока формула (8) не будет проверена. Если записать формулу (8) с частичными рангами, то значение d₀ будет таким, что:

при

*Определение d₁:

Чтобы найти d₁, используют отношение:

Значения при d=0,…,q-1 вытекают из следующим образом:

- w 1 d = w 0 d − 1 , если d-d₀

- и , если d≠d₀ (в этом случае повторяют, пока d отличается от d₀).

Приходим к той же проблеме, что и при определении компоненты d₀. Чтобы найти значение d₁, исходят из того, что d₁=0, и осуществляют последовательную инкрементацию d₁ на 1, пока не будет проверено неравенство (9)

*Определение других d_k:

Вычисление следующих d_k подобно предыдущим рассмотренным случаям. Чтобы найти значение d_k, исходят из того, что d_k=0, и осуществляют последовательную инкрементацию d_k на 1, пока не будет проверено неравенство .

После декодирования вектора D=(d₀, …, d_n-1) из него выводят вектор y путем простого транспонирования алфавита.

Индексация перестановочного кода и обратная операция являются сложными операциями. Применяемые алгоритмы используют комбинаторный анализ. Индексация комбинаций и обратная операция требуют деления произведений факториалов.

Сложность деления

Несмотря на достижения в области интегральных схем и процессоров обработки сигнала, деление остается сложной операцией. Обычно деление целого числа, представленного на 16 бит, на целое число, представленное на 16 бит, требует в 18 раз больше затрат, чем умножение. Весовой коэффициент деления 32-битового целого числа на 16-битовое целое число составляет 32, тогда как весовой коэффициент их умножения составляет 5.

Кадрирование переменных

Стоимость деления не является единственной проблемой. Кадрирование переменных является еще одной проблемой, что видно из нижеследующей таблицы 1.

На 16-битовых целых словах можно отобразить только факториалы целых чисел, меньших или равных 8. Для чисел, больших 12, представление факториалов на 32-битоых целых словах не представляется возможным.

Кроме того, сложность операций возрастает также с числом используемых бит для представления переменных. Так, деление 32-битового целого числа на 16-битовое целое число почти в два раза сложнее (весовой коэффициент 32), чем деление 16-битового целого числа (весовой коэффициент 18).

Таблица 1:
Факториалы целых чисел
n	n!	Log2(n!)
0	1	0
1	1	0
2	2	1
3	6	2.5849625
4	24	4.5849625
5	120	6.9068906
6	720	9.4918531
7	5040	12.299208
8	40320	15.299208
9	362880	18.469133
10	3628800	21.7910611
11	39916800	25.2504927
12	479001600	28.8354552
13	6227020800	32.535895
14	87178291200	36.3432499
15	1307674368000	40.2501405
16	20922789888000	44.2501405

Были предложены решения для снижения сложности операции ОР1. Проблема сложности операций ОР2 и ОР3 изучена мало. Вместе с тем, в кодер/декодер TDAC, запатентованном заявителем, или в кодер 3GPP-AMR-WB+ были внесены упрощения алгоритмов кодирования и декодирования при помощи формулы Шальквийка.

Упрощения перечисления перестановок и обратной операции (операции ОР2 и ОР3)

Вычисление ранга t перестановки и обратную операцию ускорили за счет указанных ниже упрощений вычисления n членов , определение которых можно напомнить:

, (0≤k≤n-1)

Два первых упрощения служат для снижения сложности как кодирования, так и декодирования. Третье используют при кодировании, а два последних - при декодировании.

Метод кодирования показан на фиг.2 и 3. В частности, на фиг.3 показано вычисление ранга при помощи формулы Шальквийка в рамках известных решений, тогда как на фиг.2 показаны предварительные этапы (обозначенные "ЕР-n", для n-го предварительного этапа на фиг.2).

Как показано на фиг.2, обработка начинается с этапа ЕР-1, на котором получают компоненты вектора у=(y₀, …, y_n-1). Следующий общий этап ЕР-2 предусматривает вычисление элементов алфавита для вектора А=(a₀, …, a_q-1), а также определение максимального индекса q. Для этого после этапа инициализации ЕР-21, на котором устанавливают q=1, а₀=у₀, образуют петлю на индексе k, заключенном между 1 и n-1 (завершающий тест ЕР-26 или, если нет, инкрементация ЕР-27), с целью поиска элементов a_q следующим образом:

- если компонента y_k текущего индекса k уже не находится среди элементов {а₀, …, a_q-1} (тест ЕР-22), необходимо присвоить новый элемент a_q, такой как a_q=y_k (этап ЕР-23) множеству {а₀, …, a_q-i}, и произвести инкрементацию q на 1 (этап ЕР-25).

Следующий общий предварительный этап ЕР-3 является вычислением вектора D=(d₀, …, d_n-1) следующим образом:

- при k, возрастающем от 0 до n-1 (этап ЕР-31 инициализации к на 0, завершающий тест ЕР-37 на k и инкрементация ЕР-38 если нет), находят значение d во множестве индексов (0,…, q-1), при котором y_k=a_d (тест ЕР-23 в петле на d и инкрементация ЕР-26 с d=d+1 если нет).

Далее со ссылками на фиг.3 следует описание этапов вычисления ранга t, которые следуют за предварительной обработкой, показанной на фиг.2. Этапы, показанные на фиг.3, обозначены "СА-n" для обозначения n-ого этапа кодирования в рамках известных решений.

Этап СА-1 является инициализацией ранга t на 0, переменной Р на 1 (знаменатель, участвующий в вычислении ранга на этапе СА-13) и q весовых коэффициентов w₀, …, w_q-1 на 0.

В данном случае производят декременацию значения к от n-1 до 0 (этап СА-2 инициализации к на n-1, завершающий тест СА-14 и декрементация СА-15, если нет). Преимущество такого выбора будет указано ниже. После этого используют компоненты d_k вектора D, полученного на предварительном этапе ЕР-3, и для текущего k фиксируют d=d_k (этап СА-3). Обновляют соответствующий весовой коэффициент w_d (W_d+1 на этапе СА-4) для определения члена Р (Р=P_x W_d на этапе СА-5). Производят инициализацию на 0 (этап СА-6) суммы S, участвующей в числителе при вычислении соответствующего ранга на этапе СА-13, и после этого производят петлю на индексе i весовых коэффициентов w_i (завершающий тест СА-9 и, если нет, инкрементация СА-10 до d-1) для обновления суммы S (S=S+W_i на этапе СА-8). Перед вычислением ранга t на этапе СА-13 проверяют, чтобы сумма S не равнялась нулю (тест СА-11). Преимущество этого выполнения описано ниже.

Вычисление ранга t (этап СА-13) требует использования члена-факториала (n-k-1)! следующим образом:

t=t+(S/P)(n-k-1)!

Вместо вычисления члена (n-k-1)! при каждом обновлении ранга t эти значения предварительно вводят в память и для получения текущего значения (n-k-1)! просто обращаются к памяти (этап СА-12).

Таким образом, некоторые из преимуществ обработки, показанной на фиг.3, будут использованы при применении настоящего изобретения. Эти преимущества будут уточнены ниже.

*Ведение в память факториалов

Чтобы избежать вычисления членов (n-k-1)! и w k i ! в реальном времени, значения n+1 факториалов (0!, 1!, n!) вычисляют заранее и вводят в память. Если размер n меняется до определенных пределов (n<n_max), то предварительно вычисляют и вводят в память значения 0!, 1!, …, n_max!

*Тест на накопление промежуточных весовых коэффициентов для избежания деления

Нет необходимости вычислять , если член S k = ∑ d = 0 d k − 1 w k d равен нулю. Однако этот член часто равен нулю, в частности, для первых позиций (k близок к n-1). Добавив тест на ничтожность этого члена (тест СА-11 на фиг.3), можно избежать деления (и умножения). Поскольку деление является намного более сложным, чем тест, выигрыш в сложности является значительным.

*Инверсия петли на позициях кодирования

Весовые коэффициенты (где d=0, 1,…, q-1) выводят из весовых коэффициентов путем инкрементации на 1 и повторения других значений для d≠d_k. В этом случае можно реализовать петлю (этапы СА-2, СА-14, СА-15 на фиг.3), начиная от последней позиции (k=n-1) вектора до первой (k=0). Эта «инверсированная» петля после инициализации на 1 позволяет вычислить член P_k:

,

только с одной инкрементацией и одним умножением путем итерации, то есть

и

Кроме того, можно обработать две последние позиции отдельно (k=n-1 и k=n-2).

Действительно,

- для последней позиции (k=n-1), , следовательно

- для предпоследней позиции (k=n-2),

если d_n-2>d_n-1, и , следовательно ,

если нет (d_n-2≤d_n-1), , следовательно , при P_n-2=2, если d_n-2=d_n-1, и, если нет, то P_n-2=1.

Можно также предусмотреть другие детали преимущественного выполнения, описанные ниже.

*Исключение деления при декодировании

Чтобы избежать деления при декодировании во время поиска d₀, неравенство (8) можно преобразовать следующим образом:

Точно так же, исключают деление во время поиска d₁ путем преобразования неравенства (9) следующим образом:

или даже:

Следует отметить, что, если таким образом можно исключить деление во время поиска d_k (0<k<n-1), то все равно необходимо осуществить (n-1) операций деления для вычисления (0<k<n-3).

*Тест на весовые коэффициенты при декодировании

Таким образом, в последних позициях для некоторых значений d, (для компонент значения d, занимающих позиции, предшествующие позиции k) нет необходимости вычислять члены неравенств (8) и (9) для этих значений d.

Другие проблемы известных решений: кадрирование переменных

Проблема кадрирования переменных была затронута в кодере TDAC заявителя.

Первое решение состоит в установлении четкого различия между обработкой размеров, превышающих 12, и обработкой более малых размеров. Для малых размеров (n<12) вычисления производят на 32-битовых целых числах без знака. Для более значительных размеров используют переменные двойной точности с плавающей запятой, пренебрегая возрастанием сложности вычисления (операции двойной плавающей точности стоят дороже, чем их эквиваленты по полной точности) и увеличением требуемой емкости памяти.

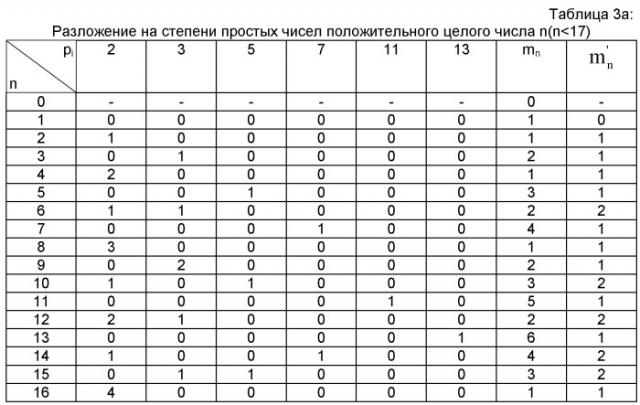
Кроме того, если максимальная точность ограничена 32-битовыми целыми числами без знака (выполняется процессорами обработки чисел с фиксированной запятой), то факториалы целых чисел более 12 не могут быть заранее введены в память напрямую, и векторы размером более 12 должны кодироваться отдельно. Для решения этой проблемы используют представление с псевдоплавающей запятой по мантиссе и показателю факториалов n! в виде 2^j×r. Это разложение подробно показано в нижеследующей таблице 2. Введение в память n! (при n меньшем или равном 16) сводится к записи в память r с точностью не более 30 бит, а также показателя степени j, который соответствует простому смещению бит.

Таблица 2:
Факторизация факториалов
n	log2 (n!)	2j	r	log2r
0	0	1	1	0
1	0	1	1	0
2	1.0000	2	1	0
3	2.5849625	2	3	1.5849625
4	4.5849625	8	3	1.5849625
5	6.9068906	8	15	3.9068906
6	9.4918531	16	45	5.4918531
7	12.299208	16	315	8.29920802
8	15.299208	128	315	8.29920802
9	18.469133	128	2835	11.469133
10	21.7910611	256	14175	13.7910611
11	25.2504927	256	155925	17.2504927
12	28.8354552	1024	467775	18.8354552
13	32.535895	1024	6081075	22.535895
14	36.3432499	2048	42567525	25.3432499
15	40.2501405	2048	638512875	29.2501405
16	44.2501405	32768	638512875	29.2501405

Таким образом, в большинстве случаев методы из предшествующего уровня техники не решают проблему кадрирования переменных с ограниченной точностью, в частности, с фиксированной запятой. Применение в кодере TDAC хотя и позволяет регулировать проблему кадрирования, но не позволяет избежать дорогостоящих операций деления двух целых чисел. Кроме того, при более значительных размерах промежуточные вычисления (например, числитель и знаменатель частичных рангов ) могут приближаться к состоянию насыщения. В этом случае представленные выше упрощения не могут быть использованы в обработке декодирования, и необходимо возвращаться к формулам неравенств (8) и (9), то есть возобновлять многочисленные операции деления.

Методы перечисления, такие как метод Шальквийка, характеризуются такими же проблемами. Как только в них применяют комбинаторный метод, они требуют вычисления произведений факториалов, а также операций их деления.

Сущность изобретения

Задачей настоящего изобретения является улучшение этой ситуации.

В этой связи его объектом прежде всего является способ кодирования/декодирования цифровых сигналов, использующий перестановочные коды с вычислением комбинаторных выражений, в котором комбинаторные выражения представлены разложениями на степени простых множителей и определяются путем считывания из памяти заранее записанных представлений разложений выбранных целых чисел.

При этом настоящее изобретение дает эффективное решение проблем, связанных как с индексацией перестановочного кода, так и с обратной операцией. Оно одновременно решает обе проблемы кадрирования переменных и деления.

Действительно, в предпочтительном варианте выполнения заранее записанные представления содержат характеристические значения показателей степени, записанные в соответствии с характеристическими значениями последовательных простых чисел для каждого из указанных целых чисел.

Таким образом, уже решается проблема из предшествующего уровня техники, связанная с кадрированием переменных.

Эта проблема кадрирования возрастает еще больше, когда речь идет об операциях с факториалами.

В предпочтительном варианте выполнения, чтобы производить операции с комбинаторными выражениями, когда они содержат значения факториалов целых чисел, заранее записанные представления содержат, по меньшей мере, представления разложений значений факториалов.

Таким образом, этот вариант выполнения позволяет снять проблему кадрирования переменных и за счет этого раздвинуть общепринятые установленные пределы, что касается размера n рассматриваемых перестановочных кодов.

Согласно другому предпочтительному отличительному признаку, по меньшей мере, одно из указанных комбинаторных выражений содержит частное от деления целого числителя на целый знаменатель, и это частное представлено в виде разложения на степени простых множителей, при этом каждая степень является разностью показателей, соответственно связанных с числителем и с знаменателем и относящихся к одному и тому же простому числу.

Таким образом, решается проблема известных решений, связанная с операциями деления, которые заменяются простыми операциями вычитания.

В первом варианте выполнения предусмотрено обращение к напоминающему устройству для поиска заранее записанного разложения одного из вышеуказанных выбранных целых чисел. Для этого заранее записанное представление выбранного целого числа хранится в адресном ЗУ, при этом обращение к указанному ЗУ дает последовательность показателей степени, присваиваемых соответствующих простым числам, для разложения выбранного целого числа.

Предпочтительно заранее записанное представление выбранного целого числа сохраняется в виде последовательности адресов, каждый из которых для простого числа дает показатель степени, присваиваемый этому простому числу, для реконструкции выбранного целого числа.

В дальнейшем этот признак первого варианта будет называться термином «разуплотненное представление разложений».

Согласно второму варианту выполнения, заранее записанные преставления сохраняются в памяти в виде слов, содержащих последовательность групп бит, при этом каждая группа имеет:

- весовой коэффициент, являющийся функцией простого числа, и

- значение, являющееся функцией показателя степени, связываемого с этим простым числом.

Предпочтительно определение простых показателей степени осуществляют в этом случае путем последовательных наложений, по меньшей мере, частичной маски на битовое слово с последовательными смещениями в зависимости от весового коэффициента бит и со считыванием остающихся бит.

В дальнейшем этот признак согласно второму варианту будет называться «уплотненное представление разложений».

Само развертывание способа для вычисления комбинаторного выражения в целом может содержать следующие этапы:

- идентификация, среди указанных выбранных целых чисел, членов, появляющихся в произведении и/или в частном, образующих указанное комбинаторное выражение,

- считывание в памяти показателей степени, участвующих в разложениях указанных членов на простые множители,

- сложение и/или соответственно вычитание считанных показателей степени для определения показателей, участвующих в разложении указанного комбинаторного выражения на степени простых множителей, и последующее вычисление указанного комбинаторного выражения на основании его разложения на степени простых множителей.

Что касается вычисления произведения, которое следует осуществлять рекуррентно и в котором при каждой рекурренции участвует новый член, то предпочтительно временно вводить в память разложение вычисления произведения, осуществленного при предыдущей рекурренции. Таким образом, если способ содержит рекуррентный этап вычисления произведения, на котором при каждой рекурренции появляется член, умножаемый на произведение, определенное во время предыдущей рекурренции:

- указанное произведение, определенное при предыдущей рекурренции, предпочтительно сохраняют в памяти в виде разложения на степени простых множителей,

- указанный член, умножаемый на произведение, предпочтительно является одним из выбранных целых чисел, разложение которых заранее введено в память, и

- для определения указанного произведения на текущей рекурренции достаточно прибавлять, по одному на простое число, показатели степени, полученные из соответствующих разложений указанного произведения, определенного на предыдущей рекурренции, и указанного члена, умножаемого на произведение.

Точно так же, если способ содержит рекуррентный этап вычисления деления, в котором на каждой рекурренции появляется член, делящий частное, определенное на предыдущей рекурренции:

- указанное частное, определенное на предыдущей рекурренции, предпочтительно сохраняют в памяти в виде разложения на степени простых множителей,

- указанный член, делящий частное, предпочтительно является одним из выбранных целых чисел, разложение которых заранее введено в память, и

- для определения указанного деления на текущей рекурренции вычитают, по одному на простое число, показатели степени, полученные из разложения указанного частного, определенного на предыдущей рекурренции.

Это временное сохранение в памяти промежуточных разложений рекуррентно вычисляемых произведений и/или частных является особенно предпочтительным для определения рекуррентных частичных рангов, накопление которых характеризует ранг перестановки.

Таким образом, в предпочтительном варианте выполнения изобретения перестановочные коды сопровождаются вычислением количества, характерного для ранга перестановки, содержащего накопление частичных рангов, при этом каждый частичный ранг соответствует в этом случае одному из указанных комбинаторных выражений.

Вычисление ранга перестановки можно применять при кодировании цифровых сигналов с векторным квантованием для индексации перестановок компонент вектора-директора (операция ОР2 на фиг.1А), причем эти перестановки были осуществлены на предварительном этапе (операция ОР1) для определения вектора-кода, наиболее близкого к входному вектору.

Точно так же, при декодировании цифровых сигналов с векторным квантованием определение ранга перестановки осуществляют в случае, когда на основании данного значения ранга перестановки:

- вычисляют, по меньшей мере, количество, характеризующее ранг перестановки (операция ОР3 на фиг.1А), приближающееся к указанному данному значению, в зависимости, по меньшей мере, от одной предполагаемой компоненты создаваемого вектора-кода,

- выбор предполагаемой компоненты подтверждают, если это количество проверяет условие близости с данным значением ранга.

В примере выполнения это условие близости проверяют, если данное значение ранга может быть охвачено накоплениями частичных рангов до частичного ранга, связанного с предполагаемой компонентой, с одной стороны, и до частичного ранга, связанного с компонентой, соответствующей инкрементации предполагаемой компоненты, с другой стороны.

Таким образом, это условие близости может соответствовать общей формуле описанных ранее неравенств (8) в случае перечисления Шальквийка;

Таким образом, настоящее изобретение предпочтительно можно применять для кодирования/декодирования источника с векторным квантованием согласно фиг.1А.

Вместе с тем, кодирование/декодирование может быть кодированием/ декодированием канала с модуляцией согласно фиг.1В, которое содержит:

- перед передачей: определение вектора-кода на основании ранга перестановки (одинаковая операция ОР3 на фиг.1А и 1В), и

- при приеме: вычисление ранга перестановки на основании вектора-кода, соответствующего принятому вектору (одинаковая операция ОР2 на фиг.1А и 1В).

Вычисление частичного ранга использует члены (в произведении или в частном), которые, как будет показано ниже, остаются меньшими или равными максимальному размеру n перестановочных кодов. Таким образом, в предпочтительном варианте выбранные целые числа, разложения которых заранее введены в память, содержат, по меньшей мере:

- целые числа от 1 до максимального размера n,

- значение факториала целого числа 0,

- и, предпочтительно,