Генератор случайных чисел на основе трехзначной логики

Генератор случайных чисел на основе трехзначной логики

Иллюстрации

Показать все

Реферат

Изобретение относится к области цифровой вычислительной техники, в частности к вычислениям методом Монте-Карло и к системам безопасности для генерации случайных ключей. Техническим результатом является увеличение скорости генерации значений на прежней или специальной элементной базе. Технический результат достигается тем, что предлагаемое устройство генерирует равномерно распределенные случайные числа в троичном коде, что повышает число вариантов сгенерированных чисел за единицу времени по сравнению с двоичным датчиком.

Заявляемое устройство относится к классу физических генераторов случайных чисел и находит применение в вычислительных устройствах по методу Монте-Карло и в системах обеспечения безопасности для генерации случайных ключей.

Известно большое количество способов генерации псевдослучайных чисел аппаратным и программным способом, однако, применение таких способов не всегда желательно. Нужны физические генераторы случайных чисел, выходы которых не возможно предсказать, легко сопрягаемые с цифровой техникой.

Известно устройство [1] для генерации случайных чисел, однако, в нем используется источник элементарных частиц и их приемник, что делает такое устройство очень дорогим.

Известно устройство [2], состоящее из разнородных устройств, содержащее элементы памяти в виде счетчика, что усложняет его изготовление. Известно устройство [3], использующее для генерации случайных чисел аналоговый хаотический генератор. Его недостатком является использование АЦП для перевода аналоговых сигналов в цифровые сигналы.

Наиболее близким техническим решением по совокупности совпадающих признаков и достигаемому техническому результату является устройство [4], составленное из сумматоров по модулю два, соединенных таким образом, что в полученной комбинационной схеме возникают обратные связи. В результате схема переходит в режим хаотической генерации случайных сигналов. Способ соединения сумматоров подбирается таким образом, чтобы схема не имела стационарных состояний. Поскольку время срабатывания каждого сумматора является физической случайной величиной, схема превращается в цифровой генератор случайных чисел. При этом доказано, что двоичный сигнал на выходе схемы имеет равномерное распределение.

Недостатком предложенной схемы является то, что сигнал на выходе является двоичной величиной. Если необходимо увеличить разрядность выхода генератора приходится набирать такой сигнал из выходов в различные моменты времени, что замедляет генерацию, либо использовать сигналы с нескольких выходов схемы, что приводит к зависимости в разрядах генерируемого сигнала.

В настоящее время известны технологические решения, позволяющие реализовать любую комбинационную схему, работающую в троичной логике [5].

Задачей заявленного технического решения (предлагаемого изобретения) является создание физического генератора случайных величин, с выхода которого в любой момент времени можно получить случайный сигнал, имеющий равномерное распределение в троичной логике.

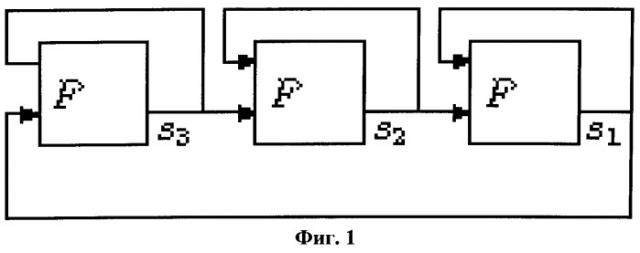
Заявленное техническое решение реализуется посредством устройства, вид которого для случая трех комбинационных схем представлен на Фиг.1.

Подобная схема может быть составлена из любого числа комбинационных схем. Каждая комбинационная схема имеет два входа, один выход и работает в трехзначной логике, реализуя одну и ту же функцию c=F(a,b), a,b,c∈{0,1,2}.

Функция определяется следующим образом: если a≠b, то с≠а&с≠b, тем самым функция определена однозначно, если аргументы не совпадают; если аргументы совпадают, то значения функции определены следующей таблицей.

	F(0,0)	F(1,1)	F(2,2)
F	1	2	0

Данную таблицу можно заменить любой таблицей, полученной из исходной, с помощью преобразования σ(F)=σ(F(σ(a),σ(b)), где σ - любая перестановка из 3 символов. N комбинационных схем соединены в кольцо. Сигнал с выхода каждой схемы поступает на один из входов той же схемы и на вход следующей за ней схемы. Генерируемый сигнал снимается с любого выхода функционального элемента S_i. Статистические свойства снимаемого сигнала обосновываются следующим образом. Время срабатывания каждой комбинационной схемы задается экспоненциальным распределением с некоторым параметром λ, одинаковым для всех схем, при этом разные схемы срабатывают независимо друг от друга. Согласно [4], в этом случае поведение генератора описывается марковским процессом с непрерывным временем, состояние которого задается выходами всех комбинационных схем. Предлагаемое соединение функциональных элементов обеспечивает существование единственного финального распределения состояний генератора. В этом финальном распределении каждое достижимое состояние имеет свою вероятность, вообще говоря, отличную от других состояний, однако, появление каждого из сигналов {0,1,2} на выходах функциональных элементов равняется 1/3. Для обеспечения независимости снимаемых сигналов нужно, чтобы время съема превосходило время установления генератора в финальное распределение состояний. Ниже (табл.2) приведены результаты вычисления времени t установления генератора для нескольких значений N числа комбинационных схем при значении параметра экспоненциального распределения λ=1. В качестве критерия близости текущего распределения вероятностей состояний к финальному распределению выбрана величина δ - среднеквадратическое отклонение распределения вероятностей состояний в момент времени t от финального распределения.

N/t	2	3	4	5	6
2	0.0095249	0.0001857	0.0000034	6.288D-08	1.141D-09
3	0.0026750	0.0000398	0.0000005	7.596D-09	1.102D-10
4	0.0014727	0.0000404	0.0000011	3.592D-08	1.113D-09
5	0.0004785	0.0000077	8.981D-08	9.856D-10	3.056D-11
6	0.0001991	0.0000055	0.0000002	6.546D-09	2.868D-10

Из представленной таблицы следует, что при выбранном значении параметра λ установление финального распределения происходит уже при t=5. Отсюда следует, что для произвольного значения λ установление финального состояние происходит через время t₀, удовлетворяющее неравенству λt₀>5.

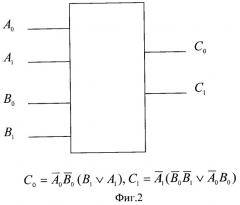
Заявленное техническое решение реализовано в виде устройства, составленного из комбинационных схем, соединенных согласно схеме, приведенной на Фиг.1, на Фиг.2 представлена эмуляций комбинационной схемы, работающей в трехзначной логике, булевской комбинационной схемой, в которой парам булевских сигналов сопоставлены сигналы троичной логики согласно правилу (0,0)→0,(0,1)→1, (1,0)→2.

Устройство состоит из N комбинационных схем F. Каждая комбинационная схема F имеет шину питания два информационных входа, один информационный выход и работает в троичной логике согласно приведенному выше описанию. Комбинационные схемы соединены кольцевым образом, при этом выход с каждой схемы поступает на вход этой же схемы и на свободный вход следующей схемы в кольцевом соединении. Состоянием устройства является набор S₁,S₂,…,S_N выходных сигналов всех комбинационных схема. Устройство работает следующим образом: при подаче питания в начальный момент состояние устройства будет произвольным. Поскольку стационарные состояния в устройстве отсутствуют, выход каждой комбинационной схемы изменится, однако, это произойдет в разные моменты времени, поскольку время срабатывания каждой схемы является случайным, и схемы работают независимо. Через моменты времени t₀, вычисленные заранее на основе параметра λ, экспоненциального распределения и числа N, снимается сигнал с выхода любой комбинационной схемы. В результате получаем независимые трехзначные случайные величины с равномерным распределением, что повышает производительность устройства в полтора раза по сравнением с аналогом, работающим в двоичной логике.

Устройство подвергнуто тестированию в качестве математической модели, в результате которого получен случайный сигнал, имеющий равномерное распределение в троичной логике, что является доказательством соответствия критерию «промышленная применимость» в лаборатории при Казанском Федеральном университете. Заявленное устройство может быть реализовано на любой стандартной элементной базе, что является доказательством соответствия заявленного технического решения критерию «промышленная применимость» предъявляемого к изобретениям.

Источники информации

1. Патент РФ 2331916.

2. Патент РФ 2281603.

3. Заявка на изобретение РФ 2009104431.

4. Кузнецов В.М., Песошин В.А., Столов Е.Л. Марковская модель цифрового стохастического генератора // Автоматика и телемеханика - 2008 - №9 - С.62-68.

5. Peiman Keshavarzian, Keivan Navi. Universal ternary logic circuit design through carbon nanotube technology // International Journal of Nanotechnology - 2009 - №10-11 - P.942-953.

Генератор случайных чисел на основе трехзначной логики, реализованный в виде кольцевого соединения N одинаковых комбинационных схем, работающих с трехзначной логикой и реализованных с помощью любой технологии, имеющих два входа и один выход, реализующих функцию c=F(a,b) a,b,с∈{0,1,2}, определенную формулой: если а≠b, то c≠a&c≠b; если аргументы совпадают, то значение функции определено таблицей

	F(0,0)	F(1,1)	F(2,2)
F	1	2	0

причем эта функция F может быть заменена новой функцией G, полученной согласно формуле G(a,b)=σ(F(σ(a), σ(b)) с помощью любой перестановки σ из трех чисел, при этом выход каждой комбинационной схемы соединен с одним из входов этой схемы и с одним из входов следующей комбинационной схемы в кольцевом соединении, а случайный сигнал снимается с выхода любой комбинационной схемы.