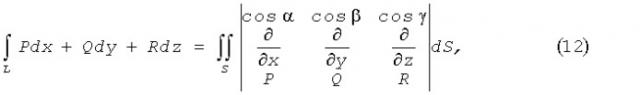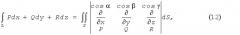Равновесный локально-термодинамический проницаемый тепловой излучатель с выровненным распределением потенциалов в пространстве

Равновесный локально-термодинамический проницаемый тепловой излучатель с выровненным распределением потенциалов в пространстве

Иллюстрации

Показать все

Реферат

Заявляемое техническое решение относится к области электронагревательных приборов, предназначенных для подогрева и испарения воды в расходном режиме и в составе замкнутых водяных и пароводяных контуров.

«Уровень техники». Известен электродный водонагреватель (реферат заявки на изобретение RU 95114849 от 04.09.95 г., опубл. Б.И. 20.08.1997, F24H 1/20), содержащий перфорированные электроды, которые установлены на равном расстоянии с образованием сквозных каналов и расположены по электрическим фазам поочередно. Электродный водонагреватель работает следующим образом: подогреваемая вода поступает через входной патрубок, и, проходя сквозь проницаемые электроды, нагревается, как рабочая среда печи сопротивления; движение рабочей среды может осуществляться за счет напора гидравлической сети (расходный режим) или за счет естественной циркуляции (в режиме замкнутого контура).

Задачей изобретения является выравнивание распределения потенциалов в пространстве проницаемых тепловых излучателей.

Для решения поставленной задачи в равновесном локально-термодинамическом проницаемом тепловом излучателе с выровненным распределением потенциалов в пространстве, содержащем перфорированные электроды, которые установлены на равном расстоянии с образованием сквозных каналов и расположены по электрическим фазам поочередно, предлагается отверстие электрода выполнять в виде округлого отверстия.

Анализ пропекающих процессов в пространстве протираемого теплового излучателя целесообразно проводить с помощью теории подобия.

Предлагаемое решение основывается на теории подобия элементарного вибратора с элементами аналогии.

1) Исследование электродных систем представляет важное значение в связи с увеличением области применения данных систем для решения производственных задач. Теоретический и практический интерес представляет исследование и моделирование электромагнитных процессов, протекающих в различных пространственно-энергетических областях энергоустановок. Например, рассмотрим электродную систему.

Если есть отверстие в плоскости, то в окружающем пространстве появляется искажение электромагнитного поля за счет нарушения экранировки.

Определение поля сводится к решению двух задач:

- нахождение распределения поля между краями отверстия (внутренняя задача);

- нахождение распределения поля за экраном, по распределению поля между краями отверстия (внешняя задача).

1 Решение первой (внутренней) задачи встречает определенные трудности.

Применяется упрощение - отверстие не вносит каких-либо искажений в распределение поверхностных токов. Тогда токи смещения в отверстии являются продолжением токов проводимости. Зная связь между током смещения и напряженностью электрического поля, можно найти параметры поля между краями отверстия.

Если длина отверстия значительно меньше длины волны - элементарное отверстие (поле в отверстии Е₀ или напряжение между краями отверстия U₀ квазистационарны).

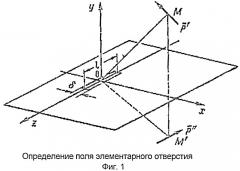
Квазистационарность можно охарактеризовать следующим образом - для каждого момента времени напряжения между краями отверстия по всей длине имеет одно и то же значение (Фиг.1).

Анализ протекающих процессов в пространстве проницаемого теплового излучателя целесообразно проводить с помощью теории подобия.

Предлагаемое решение основывается на теории подобия элементарного вибратора с элементами аналогии.

Аналогия основывается на конструктивном и теоретическом подобии того, как провод элементарного вибратора заканчивается металлическими шариками, так и прямоугольное отверстие с торца выполняется в виде округлых отверстий. Данная аналогия теоретически обоснованна исходя из следующих оснований.

Конструктивно аналогию можно обосновать следующим образом. Основой анализа является элементарный электрический вибратор.

Элементарный электрический вибратор - бесконечно малый элемент линейного электрического тока (идеальный вибратор - с параметрами тока одинаковыми по амплитуде и фазе). Практической реализацией элементарного электрического вибратора является «диполь Герца» (короткий провод (сравнивается с длиной волны) с шарами на концах, ток, вдоль которого (обтекаемого током) мало меняется по амплитуде).

«Вибратор Герца» («диполь Герца») - простейшая антенна, медный стержень с металлическими шарами (или полосами) на концах, в разрыв которого (искровой промежуток), включается катушка Румкорфа (в режиме излучения) или нагрузки (в режиме приема). Диполь Герца применялся Генрихом Герцем (1888 г.) в опытах по подтверждению существования электромагнитных волн.

«Катушка Румкорфа» (англ., «Induction coil») - устройство для преобразования первичного постоянного тока во вторичный переменный ток высокого напряжения, для получения импульсов высокого напряжения (трансформатор). Индукционную катушку, генерирующую токи высокой частоты, в 1851 г. изобрел Румкорф (Ruhmkorff) Генрих Даниэль (1803-1877).

Конструктивно «катушка Румкорфа» состоит из цилиндрической части, с центральным железным стержнем внутри, на которую намотана первичная обмотка из толстой проволоки.

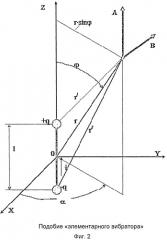
Подобие «элементарного вибратора» (Фиг.2) теоретически обосновывается следующим образом.

Для объяснения полученных результатов исследований - это особенность распределения электромагнитного поля.

Известно, что при исследовании электромагнитного поля, излучаемого антенной, принято все пространство вокруг антенны подразделять на «ближнюю», «среднюю» (или «промежуточную») и «дальнюю зоны».

«Ближняя зона» ограничивается радиусом, величина которого много меньше длины волны (r<<1). «Дальняя зона» расположена от антенны на расстоянии, намного превышающем длину волны (r>>1). В «средней зоне» расстояние от антенны до любой точки соизмеримо с длиной волны.

В «ближней зоне» энергия излучения не учитывается. Границы ближней зоны зависят от частоты: чем выше частота, тем ближе граница зоны к источнику.

Особенностью рассмотрения теплового излучателя является параметры питающей электрической сети (например, частота f=50 Гц). Для этих параметров длина волны составляет l=6000 км. При данном упрощении практически на любом расстоянии от излучателя пространство может теоретически определяться как «ближняя зона».

Данные исследований позволяют говорить, что распределения энергии излучения в «ближней зоне» также характеризуется рядом интересных особенностей.

Если рассматривать радиочастотный диапазон: при параметрах частот порядка значений 10¹⁰ Гц и выше, длина волны измеряется в сантиметрах (дальняя зона).

«Ближняя зона» (зона «квазистационарности») характеризуется постоянством во времени мгновенных значений векторов переменного поля (законы постоянных во времени полей).

Аналитически аналогию можно обосновать следующим образом. Особенностью распределения волновых процессов потенциалов в «дальней зоне» («зоне излучения») является преобладание составляющих Е и Н, меняющихся пропорционально l/r и совпадающих по фазе. Основываясь на данных упрощениях можно в известных выражениях для H_a и E_j пренебречь всеми членами, кроме первых.

Известно, что волна, имеющая такой характер, называется сферической, она имеет структуру поля волны типа ТЕМ (буквами ТЕМ обозначают поперечные волны, то есть такие волны, у которых в направлении распространения отсутствуют составляющие векторов напряженностей электрического и магнитного полей).

Таким образом, в сферической волне и в плоской, энергия электрического поля равна энергии магнитного поля (eE²=mH²).

Эквифазная поверхность сферы (радиус r=const} характеризуется одинаковой фазой колебания напряженности магнитного поля H в конкретный момент времени и отличается амплитудой (зависит от угла j) (определяется аргументом косинуса).

Амплитуда колебаний напряженности варьируется от нулевого значения на «полюсах» до максимального - на «экваторе» (плоскости перпендикулярной оси вибратора и проходящей через его середину). Характеристику свободно распространяющейся энергии (активной мощности) определяет совпадение но фазе Н и Е. Данная особенность может объяснять полученные результаты исследований.

Диаграмма зависимости модуля Е (энергии электрического) или Н (энергии магнитного) в дальней зоне называется «диаграммой направленности» (элементарный электрический вибратор обладает направленными свойствами).

Диаграмму зависимости векторов Е и Н в дальней зоне от угла θ называют диаграммой направленности (Фиг.3).

Выражение вектора Пойнтинга для дальней зоны:

П → R = [ E → θ ; H → α ] ;

Модуль вектора Пойнтинга (мгновенное значение):

П R = z в ( d l ) 2 Im 2 sin 2 θ 4 R 2 λ 2 ⋅ C O S 2 ( ω t − ω R υ + ϕ ) ;                 ( 1 )

П С Р = 1 T ∫ 0 T П R d t .           ( 2 )

Вектор Пойнтинга направлен по радиусу, а среднее значение его модуля за период: T = 2 π ω .

Максимальное излучение (максимальная напряженность поля) наблюдается в экваториальной (меридиональной) плоскости (Фиг.4, 5). Диаграмма (форма восьмерки) характеризует зависимость Е и Н от j в «дальней зоне».

Численно мощность, излучаемая элементарным электрическим вибратором, определяется путем интегрирования вектора Пойнтинга по эквифазной поверхности (радиус поверхности выбирается достаточно большим, чтобы она находилась в дальней зоне). Вектор Пойтинга назван по имени английского физика Дж.Г. Пойнтинга (J.H. Poynting; 1852-1914).

Проблемы электромагнитной массы рассматривались в копне XIX века. Умовым (1873 г.) был сформулирован закон сохранения энергии для движущихся сред. Пойнтингом был доказан закон сохранения для электромагнитных волн (1884 г.). Томсон определил, что потенциальная энергия связана с полем неподвижного заряда, а кинетическая энергия - с магнитным полем движущегося заряда.

Лоренц привел уравнения Максвелла к волновым уравнениям (поле заряда и электромагнитная волна имеют общую природу и описываются уравнением с запаздывающими потенциалами). Это подтвердилось «Специальной теорией относительности». Однако оказалось, что в рамках «запаздывающих потенциалов» проблема электромагнитной массы не имеет удовлетворительного решения.

Теоретически определена эквивалентность массы и энергии как современная физическая концепция, согласно которой масса тела является мерой энергии, заключенной в нем, т.е. масса неподвижного тела (так называемая масса покоя) является мерой внутренней энергии этого тела и любому виду энергии соответствует некая масса. Например, было введено понятие «релятивистской массы» как характеристики кинетической энергии движущегося тела.

Принцип сформулирован А.Эйнштейном в 1905 году. Энергия тела равна массе тела, умноженной на размерный множитель квадрата скорости света в вакууме:

Е=mc²,

где Е - энергия тела, m - его масса, с - скорость света в вакууме, равная 299 792 458 м/с.

Однако определение полной эквивалентности массы любому виду энергии не является правильным и термин «релятивистская масса» профессионально не применяется, а когда говорят о массе, имеют в виду массу покоящегося тела, а «релятивистская масса» - инертность свойств движущегося тела.

Эквивалентность массы тела запасенной в теле энергии - главный практически важный результат специальной теории относительности.

Известно, что понятие напряженности магнитного поля построено на формальной аналогии полей неподвижных зарядов и неподвижных намагниченных тел. Такая аналогия часто оказывается весьма полезной, т.к. позволяет перенести в теорию магнитного поля методы, разработанные для электростатических полей.

Напряженность магнитного поля первоначально была введена в форме закона Кулона через понятие магнитной массы, аналогичной электрическому заряду, как механическая сила взаимодействия двух точечных магнитных масс в однородной среде, которая пропорциональна произведению этих масс и обратно пропорциональна квадрату расстояния между ними:

f = k m 1 m 2 r 2 ,

где m₁ и m₂ - взаимодействующие магнитные массы; r - расстояние между точками, в которых магнитные массы считаются сосредоточенными; k - коэффициент, зависящий от свойств среды и системы единиц измерения.

Сила f направлена по прямой, соединяющей центры магнитных масс. Магнитные массы одного знака отталкиваются, а противоположного - притягиваются.

Электромагнитное поле характеризуется собственной энергией поля. Полная энергия определяется суммой энергий электрического и магнитного полей. Электромагнитное поле занимает замкнутый объем V, то:

W = W э л + W М А Г Н = ∫ V E → ⋅ D → 2 d V + ∫ V B → ⋅ H → 2 d V                   ( 3 )

Энергия электромагнитного поля не может оставаться постоянной величиной. На изменение энергии внутри замкнутого объема влияют следующие факторы:

- часть энергии электромагнитного поля может превратиться в другие виды энергии, например, механическую;

- внутри замкнутого объема могут действовать сторонние силы, которые могут увеличивать или уменьшать энергию электромагнитного поля, заключенную в рассматриваемом объеме;

- рассматриваемый замкнутый объем V может обмениваться энергией с окружающими телами за счет процесса излучения энергии.

Интенсивность излучения характеризуется вектором Пойнтинга П → . Объем V имеет замкнутую поверхность S. Изменение энергии электромагнитного поля можно рассматривать как поток вектора Пойнтинга сквозь замкнутую поверхность S (Фиг.6), т.е. ∫ S П → d S → , причем возможны варианты ∫ S П → d S → > 0, ∫ S П → d S → < 0 , ∫ S П → d S → = 0 . Нормаль, проведенная к поверхности d S ⇀ , всегда является внешней (Фиг.6).

Вектор Пойтннга - вектор плотности потока электромагнитной энергии в любой момент времени направлен по радиусу в сторону от диполя:

П → = [ E ⇀ , H → ] ,

где E ⇀ , H → - это мгновенные значения напряженности поля.

∮ S П ⇀ d S → = ∫ V d i v П → d V = ∫ V d i v [ E → , H ⇀ ] d V = ∫ V ( H → r o t E → − E → r o t H → ) d V .         ( 4 )

Переход от интеграла по поверхности d S ⇀ к интегралу по объему V осуществляется на основе теоремы Остроградского-Гаусса.

Зная, что r o t H → = ∂ D → ∂ t + σ ⋅ E → + J → C T , r o t E → = − ∂ B ∂ T , подставим эти выражения в формулу (2). После преобразования получим выражение в виде:

∮ П → d S → = − σ ∫ ( E → E ⇀ ) d V − ∫ V ( J ⇀ C T E → ) d V − ∫ V ( ∂ D → ∂ t ⋅ E ⇀ + ∂ B → ∂ t ⋅ H ⇀ ) d V             ( 5 )

Из (3) левая часть выражается суммой, состоящей из трех слагаемых.

Слагаемое P = σ ∫ ( E → E ⇀ ) d V - мгновенная мощность потерь, обусловленная в замкнутом объеме токами проводимости (тепловые потери энергии поля).

Второе слагаемое P C T O P = ∫ V ( J ⇀ C T E → ) d V - работа сторонних сил, произведенная в единицу времени (мощность Р_СТОР>0, Р_СТОР<0).

Если Р_СТОР> - в объеме V добавляется энергия (сторонние силы - генератор). Если Р_СТОР<0 - в объеме V происходит уменьшение энергии (сторонние силы - нагрузка).

Последнее слагаемое для линейной среды - скорость изменения энергии электромагнитного поля внутри объема V:

∂ ∂ t ∫ V ( E → ⋅ D → 2 + H → ⋅ B ⇀ 2 )   d V = ∂ ∂ t ∫ V ( w э + w м )     d V .                   ( 6 )

Таким образом, формула (3) - в виде:

∮ П → d S → = − P П О Т − Р С Т О Р = − ∂ ∂ t ∫ V ( w э + w м ) d V                   ( 7 )

- теорема Пойнтинга (характеризует баланс энергии внутри произвольной области, в которой существует электромагнитное поле).

Таким образом, чем больше сопротивление излучения R, тем больше излученная мощность при том же токе I. Из анализа формул (1) и (2) видно, что сопротивление излучения пропорционально квадрату длины излучателя и, что особенно важно, обратно пропорционально квадрату длины волны l. Так как длина волны l=u/f, то излученная мощность пропорциональна квадрату частоты. Если частота мала, например всего 50 Гц, то излучения практически нет. При радиочастоте излучение значительно. Например, при частоте 50 МГц излучение больше, чем при частоте 50 Гц, в 10¹² раз.

Рассмотрели электромагнитное поле, излучаемое элементарным электрическим вибратором. Для решения некоторых задач по определению электромагнитного поля удобнее пользоваться понятием элементарного магнитного вибратора.

Таким вибратором называют элемент линейного магнитного тока I_м или линейный элемент, на поверхности которого имеется ненулевая тангенциальная составляющая вектора напряженности электрического поля Е, перпендикулярная оси элемента, а тангенциальная составляющая вектора напряженности магнитного поля Н равна нулю.

В дальней зоне, где можно пренебречь составляющими, пропорциональными l/r² и l/r³, напряженности полей элементарного магнитного вибратора равны (Фиг.7):

E ˙ E = − j I ˙ m l 2 p λ sin ϕ e − j 2 π λ τ ;             ( 8 )

H ˙ ϕ = j I ˙ m l 2 x λ r E sin ϕ e − j 2 π λ τ ;             ( 9 )

E ˙ τ = E ˙ ϕ = H ˙ E = H ˙ τ = 0.           ( 10 )

Поле элементарного магнитного вибратора имеет одинаковую структуру поля элементарного электрического вибратора (Е и Н меняются местами).

Вариант магнитного вибратора - проницаемый излучатель (щелевая антенна). Элементарный проницаемый излучатель - это тонкий металлический лист с высокой проводимостью, в котором прорезана щель, длина которой l много меньше длины волны (l<<l и значительно больше ширины щели a (l>>a). Для генерации излучения подводится ЭДС к периметру пластины (Фиг.1) для разрезания токов проводимости.

Излучатель может характеризоваться бесконечной проводимостью и одинаковой напряженностью электрического поля вдоль длины щели по величине и фазе равной Е₀ (диполь Герца) (Фиг.2) или конечными размерами с тангенциальным электрическим полем и отсутствием тангенциального магнитного поля. Поэтому проницаемый излучатель характеризуется параметрами элементарного магнитного вибратора и напряженностью полей по формулам магнитного вибратора.

2. Решение внешней задачи - определение электромагнитного поля в полупространстве за экраном теплового излучателя, в котором прорезано отверстие, производится с помощью леммы Лоренца, согласно которой для двух независимых электромагнитных полей E ¯ ,   Н ¯     и     E ¯ ,   Н ¯ (напряженности электрического и магнитного поля), изменяющихся по одному гармоническому закону, имеет место соотношение:

∫ S ( E ¯ × H ¯ ′ − E ¯ ′ × H ¯ ) d s ¯ = ∫ V ( j ¯ × E ¯ ′ − j ¯ ′ × E ¯ ) d V                 ( 10 )

где s - поверхность экрана, a s₁ - та часть плоскости xoz, которая ограничена щелью.

Лемма Лоренца связывает два независимых поля на границе некоторого объема с полем внутри объема. В качестве аналога леммы Лоренца можно указать формулу Грина, которая находит широкое применение в математической физике (связывает двойной и криволинейный интеграл).

Формула Грина

Пусть G - плоская область и ее граница L является кусочно-гладким контуром. Пусть в замкнутой области G ¯ заданы функции Р(x, y), Q(x, y), непрерывные на G ¯ вместе со своими частными производными. Тогда справедлива формула:

∬ G ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y = ∫ L P d x + Q d y               ( 11 )

Формула Стокса

Пусть S простая гладкая двусторонняя поверхность, ограниченная кусочно-гладким контуром L. Формула Стокса:

∫ L P d x + Q d y + R d z = ∬ S ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y + ( ∂ R ∂ y − ∂ Q ∂ z ) d y d z + ( ∂ P ∂ z − ∂ R ∂ x ) d z d x             .

Или если заменить поверхностный интеграл второго рода на поверхностный интеграл первого рода, то получим:

∫ L P d x + Q d y + R d z = ∬ S | cos α cos β cos γ ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R | d S ,                         ( 12 )            

где cosα, cosβ, cosγ означают направляющие косинусы нормали, отвечающей выбранной стороне поверхности.

Полагая a ⇀ = ( P , Q , R ) , эту формулу можно переписать так: ∫ l a → d r ⇀ = ∬ V r o t a ⇀ d S → , т.е. циркуляция векторного поля по контуру L равна потоку вихря этого поля через поверхность S, ограниченную контуром L.

Формула Остроградского

Аналог формулы Грина для тройных интегралов. Пусть тело V ограничено кусочно-гладкой поверхностью S, тогда ∭ V ( ∂ P ∂ y + ∂ Q ∂ x + ∂ R ∂ z ) d x d y d z ∬ S P d x d y + Q d z d x + R d x d y   , или, если заменить поверхностный интеграл второго рода на поверхностный интеграл первого рода: ∭ V ( ∂ P ∂ y + ∂ Q ∂ x + ∂ R ∂ z ) d x d y d z ∬ S ( P cos α + Q cos β + R cos γ )   d S .

Полагая a ⇀ = ( P , Q , R ) , эту формулу можно переписать в виде:

∭ G d i v a → d x d y d z = ∬ S + a → d S → +                         ( 13 )

т.е. интеграл по области от дивергенции векторного поля равен потоку этого поля через поверхность, ограничивающую данную область.

Формулы Грина, Стокса и Остроградского выражают интеграл, распространенный на некоторый геометрический образ, через интеграл, взятый по границе этого образа. При этом формула Грина относится к случаю двумерного пространства, формула Стокса - к случаю двумерного «кривого» пространства, а формула Остроградского - к случаю трехмерного пространства.

На основную формулу интегрального исчисления:

∫ a b f ( x ) = f ( b ) = f ( a )

можно смотреть как на некоторый аналог этих формул для одномерного пространства.

Для определения поля E ¯   и   H ¯ в некоторой точке M(x₀, y₀, z₀) размещаем в точке М элементарный вибратор, где P ¯ - момент вибратора.

Направление вектора P ¯ определяется произвольно. Тангенциальная составляющая вектора напряженности электрического поля на поверхности плоскости электрода обращается в нуль при зеркальном изображении вибратора P ¯ относительно плоскости электрода.

Разложим вектор p ¯ ′