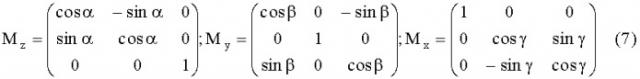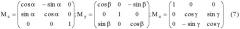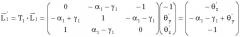Устройство для определения углового отклонения оси лазерного пучка от номинального положения

Устройство для определения углового отклонения оси лазерного пучка от номинального положения

Иллюстрации

Показать все

Реферат

Изобретение относится к области оптического приборостроения, точнее - к оптическим призменным системам, предназначенным для определения углового отклонения оси лазерного пучка от номинального положения.

Оптические оси приемного и передающего каналов лазерных систем должны быть выставлены с необходимой точностью. В некоторых случаях это удается обеспечить на стадии заводской юстировки. К таким системам относятся малогабаритные оптические дальномеры, лазерные системы видения. Они отличаются сравнительно невысокими требованиями по юстировки осей каналов - погрешности выставки могут достигать нескольких угловых минут.

Для целого ряда современных локационных систем выдвигаются очень высокие требования по точности юстировки приемо-передающих каналов - погрешности их взаимной выставки не должны превышать нескольких угловых секунд. Как правило, такие системы имеют значительные габариты, вес, они могут быть подвержены воздействию внешних механических вибраций и температурным уводам элементов конструкции. Требования по точности юстировки каналов таких систем могут быть выполнены только с использованием систем автоюстировки (САЮ).

Принцип организации подобной САЮ заключается в следующем. Часть пучка излучения рабочего лазера передающего канала на выходе системы формирования с помощью призменной системы (ПС) заводится в приемный канал, меняя направление распространения в точности на обратное. Отведенный пучок в приемном канале является репером пространственного положения оси диаграммы направленности излучения рабочего лазера, сформированного в передающем канале. В приемном канале измеряется его угловое рассогласование с осью приемного канала, которое в реальном масштабе времени отрабатывается корректирующими элементами оптической системы.

В большинстве случаев в приемный канал целесообразно отводить пучок излучения не рабочего лазера, а дополнительного маркерного источника излучения, имеющего гораздо меньшую мощность и поперечные размеры. Предварительно его ось выставляется на входе оптической системы передающего канала относительно оси пучка излучения рабочего лазера с высокой точностью.

Как видно, погрешности определения углового рассогласования определяются погрешностью переноса пучка, поэтому ПС в такой САЮ играет ключевую роль. Схемы их построения должны быть обоснованы с учетом условий функционирования, а точностные характеристики каждой схемы должны быть тщательно исследованы.

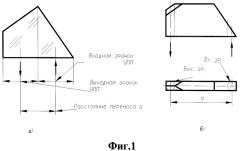
Известно, что уголковый отражатель с двугранными углами между отражающими гранями, равными 90°, является идеальным световозвращателем [Барышников Н.В., Карасик В.Е., Степанов P.O. Исследование отражательных характеристик тетраэдрических световозвращателей в ИК диапазоне. Вестник МГТУ им. Н.Э.Баумана. Сер. «Приборостроение», 2010. №1, С.3-16]. Он отражает падающее на него излучение точно в обратном направлении (см. фиг.1a). Матрица М_УО его действия имеет следующий вид:

М У О = ( − 1 0 0 0 − 1 0 0 0 − 1 )                                                                     ( 1 )

Теоретически - это идеальный вариант ПС. Однако расстояние а переноса оси пучка излучения минимально и оно ограничено конструктивными параметрами уголкового отражателя и технологическими возможностями его изготовления.

Модификация конструкции уголкового отражателя - УО с разнесенными входным и выходным зрачками (см. фиг.1б) обеспечивает несколько большие значения расстояния переноса a - до 100…200 мм. На этом возможности уголкового отражателя ограничиваются.

Известно устройство для определения углового отклонения оси лазерного пучка от номинального положения (см. фиг.2), которое является ближайшим аналогом и включает призменную систему, содержащую оптически связанные ромб призму 1, уголковый отражатель и ромб-призму 2 (Н.В. Барышников, В.В. Карачунский, В.И. Козинцев А.С. Румянцев, Д.В. Худяков, Использование методов полунатурного моделирования для исследования характеристик системы автоюстировки Тезисы докладов IV НТК «Радиооптические технологии в приборостроении», Сочи, 2006 г., с.105-108). Эта система обеспечивает большие значения расстояния переноса a.

Идеально изготовленная ромб-призма осуществляет поперечное смещение оси падающего пучка, не меняя его направления. Матрица ее действия М_РП имеет следующий вид:

М Р П = ( 1 0 0 0 1 0 0 0 1 )

Действие рассматриваемой ПС можно описать матрицей M:

М = М Р П 2 ⋅ М У О ⋅ М Р П 1 = ( − 1 0 0 0 − 1 0 0 0 − 1 ) = ​ М У О

Нетрудно заметить, что матрица M соответствует матрице уголкового отражателя (1).

Каждая из трех оптических деталей схемы при малых собственных угловых смещениях идеально переносит ось пучка, поэтому такая система инвариантна к механическим вибрациям и температурным уводам механических оправ. На качество переноса могут повлиять только собственные температурные деформации уголкового отражателя и ромб-призм, а также погрешности их изготовления.

Для увеличения расстояния переноса a в схему ПС можно включить дополнительные ромб-призмы. Их максимальное количество определяется только светопропусканием призменной системы, а также массогабаритными ограничениями.

Однако существует принципиальный недостаток рассмотренных выше схем. Он связан с тем, что элементы конструкции ПС могут располагаются на выходе формирующей оптической системы передающего канала, в сечении пучка высокоэнергетического рабочего лазера. Это обстоятельство вызывает многочисленные проблемы, связанные с защитой конструкции самой ПС от излучения рабочего лазера, а также с нарушениями пространственной структуры формируемого пучка рабочего лазера, вызванные его экранированием.

Технический результат, достигаемый при реализации предлагаемого изобретения, заключается в обеспечении возможности определения углового отклонения оси лазерного пучка от номинального положения при использовании высокоэнергетического лазера и с одновременным уменьшением экранирования сечения его пучка в условиях внешних механических воздействий, приводящих к угловым уводам призм призменной системы.

Указанный технический результат достигается за счет того, что в устройстве для определения углового отклонения оси лазерного пучка от номинального положения, содержащем призменную систему, указанная призменная система включает первую пару пентапризм, содержащую первую и вторую пентапризмы, главные сечения которых расположены в одной плоскости Р, оптический клин, склеенный с первой отражающей гранью первой пентапризмы и выполненный так, что его выходная грань параллельна входной грани первой пентапризмы, причем поверхность склейки имеет светоделительное покрытие, вторую пару пентапризм, содержащую третью и четвертую пентапризмы, главные сечения которых расположены в одной плоскости Р', при этом входная грань третьей пентапризмы расположена за выходной гранью оптического клина и параллельна ей, плоскости Р и Р' расположены под углом 2φ друг к другу, а вторая и четвертая пентапризмы оптически связаны с объективом, в фокальной плоскости которого расположен координатно-чувствительный фотоприемник, выход которого связан со входом микропроцессора.

При этом микропроцессор может быть выполнен с возможностью вычисления углового отклонения θ_Z, θ_Y оси контролируемого пучка от номинального положения на входе первой пентапризмы по формулам:

θ_z=(-θ_y1sinφ+θ_z1cosφ+θ_y2sinφ+θ_z2cosφ)/2cosφ,

θ_y=(θ_y2sinφ+θ_z2cosφ+θ_y1sinφ-θ_z1cosφ)/2sinφ,

где θ_y1; θ_z1 - угловое отклонение от номинального положения оси лазерного пучка, прошедшего первую и вторую пентапризмы;

θ_y2; θ_z2 - угловое отклонение от номинального, положения оси лазерного пучка, прошедшего первую, третью и четвертую пентапризмы.

В предлагаемом устройстве за счет того, что вместо системы призм в виде моноблока, как в ближайшем аналоге, используются отдельные пентапризмы, обеспечивается уменьшение экранирования сечения его пучка. При этом оптические свойства пентапризм позволяет создать призменную систему, обеспечивающую определение углового отклонения оси лазерного пучка от номинального положения в условиях внешних механических воздействий, приводящих к угловым уводам призм призменной системы.

Изобретение более подробно описывается с помощью чертежей.

На фиг.1а, 1б показана призменная система на основе уголкового отражателя.

На фиг.2 показана призменная система ближайшего аналога на основе уголкового отражателя и двух ромб-призм.

На фиг.3 показано расположение призменной системы устройства для определения углового отклонения оси лазерного пучка от номинального положения в локационной станции.

На фиг.4 показана схема, иллюстрирующая определение углового отклонение от номинального положения оси лазерного пучка с помощью координатно-чувствительного фотоприемника при отсутствии угловых уводов призм призменной системы.

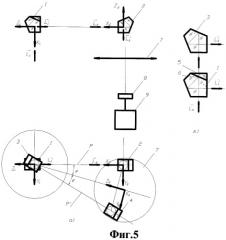
На фиг.5 показана призменная система предлагаемого устройства на основе двух пар пентапризм.

На фиг.6 показано расположение системы координат XYZ и связанной с ней нормали N ¯ по отношению к входной грани пентапризмы.

На фиг.4 показана схема, иллюстрирующая определение углового отклонение от номинального положения оси лазерного пучка с помощью координатно-чувствительного фотоприемника при отсутствии угловых уводов призм призменной системы.

Система координат XYZ связана с оптической осью системы, образованной объективом и координатно-чувствительным, например, матричным фотоприемником, расположенным в его фокальной плоскости. Центр координат O совпадает с нулевым чувствительным элементом матричного фотоприемника. При этом обычно в качестве нулевого элемента используется элемент, расположенный в центре матрицы чувствительных элементов. Ось OX выбранной системы координат XYZ совпадает с оптической осью системы, образованной объективом и матричным фотоприемником, расположенным в его фокальной плоскости, и проходит через кардинальные точки объектива и нулевой элемент матричного фотоприемника.

Таким образом, для того, чтобы определить угловой отклонение оси пучка по двум координатам, надо измерить линейные координаты Z1 и Y1 зарегистрированного на матричном фотоприемнике, расположенном в фокальной плоскости объектива, пятна распределения от контролируемого пучка излучения лазера. При этом угловое отклонение θ_Y в плоскости XOY может быть определено из математического выражения

tg(θ_Y)=Y1/f',

где f' - фокусное расстояние объектива.

Аналогично, угловое отклонение θ_Z в плоскости XOZ (на фиг.4 не показано) может быть определено из математического выражения

tg(θ_Z)=Z1/f'.

При этом, как правило, измеряемые угловые отклонения малы, они составляют несколько угловых секунд. Поэтому тангенсом можно пренебречь, т.е. использовать следующие выражения:

θ_Y=Y1/f', θ_Z=Z1/f'

На фиг.5 показана призменная система предлагаемого устройства на основе двух пар пентапризм.

Как известно, пентапризма изменяет в пространстве вектор направления падающего на нее пучка на 90 градусов по одной оси, причем этот угол инвариантен к малым угловым уводом самой пентапризмы. Используя пару пентапризм, можно обеспечить обратное отражение излучения лазера и измерение в приемном канале углового отклонения, но только по одной оси.

Для измерения угловых отклонений по двум осям в условиях внешних механических воздействий, приводящим к угловым уводам самих призм, предлагается устройство, которое содержит призменную систему, включающую первую пару пентапризм, содержащую первую 1 и вторую 2 пентапризмы. Главные сечения этих пентапризм расположены в одной плоскости Р. Вторая пара пентапризм содержит третью 3 и четвертую 4 пентапризмы, главные сечения которых расположены в одной плоскости Р'. Плоскости Р и Р' расположены под углом 2φ друг к другу. Разделение лазерного пучка между парами призм осуществляется с помощью оптического клина 5, имеющего тот же показатель преломления, что и первая 1 пентапризма, и склеенного с первой отражающей гранью первой 1 пентапризмы, причем поверхность склейки 6 имеет светоделительное полуотражающее покрытие, а выходная грань клина параллельна входной грани первой 1 пентапризмы. Входная грань третьей 3 пентапризмы расположена за выходной гранью оптического клина 5 и параллельна ей. На выходе второй 2 и четвертой 4 пентапризм расположен объектив 7, в фокальной плоскости которого расположен координатно-чувствительный фотоприемник 8, выход которого связан со входом микропроцессора 9.

При этом микропроцессор выполнен с возможностью вычисления углового отклонения θ_Z, θ_Y оси контролируемого пучка от номинального положения на входе первой 1 пентапризмы по формулам:

θ_z=(-θ_y1sinφ+θ_z1cosφ+θ_y2sinφ+θ_z2cosφ)/2cosφ,

θ_y=(θ_y2sinφ+θ_z2cosφ+θ_y1sinφ-θ_z1cosφ)/2sinφ,

где θ_y1; θ_z1 - угловое отклонение от номинального положения оси лазерного пучка, прошедшего первую 1 и вторую 2 пентапризмы;

θ_y2, θ_z2 - угловое отклонение от номинального положения оси лазерного пучка, прошедшего первую 1, третью 3 и четвертую 4 пентапризмы.

Проследим преобразование такой призменной системой вектора L → 0 луча, характеризующего направление пучка лазерного излучения на входе в призменную систему, т.е. на выходе передающего канала локационной системы.

Свяжем с оптической осью объектива приемного канала систему координат X₀Y₀Z₀. Ось OX₀ направим по оптической оси объектива приемного канала.

В этой же системе координат будем в дальнейшем определять направление вектора L → n p , характеризующего направление пучка излучения лазера на входе объектива приемного канала системы. Вектор L → 0 в системе координат X₀Y₀Z₀ выражается следующим образом:

L → 0 = ( − 1 θ y θ z ) ,                                                                     ( 5 )

где θ_y и θ_z - углы отклонения оси излучения лазера от идеального направления, вызванные разъюстировками системы. Именно эти углы необходимо измерить в приемном канале.

Получим несколько общих выражений для матриц преобразования пентапризмы. Эти выражения в дальнейшем будем использовать для описания преобразования вектора L → направления оси излучения лазера парой пентапризм, пространственное положение каждой из которых имеет отступления от идеального.

Рассмотрим систему координат XYZ (см. фиг.6) и связанную с ней нормаль N ¯ к входной грани пентапризмы.

1. Матрицы П' и П'' действия идеальной пентапризмы соответственно в прямом и в обратном ходе, записанные в приведенной системе координат, определяются известным образом [Вычислительная оптика: Справочник / М.М. Русинов, А.П. Грамматин, П.Д. Иванов и др. Под общ. ред. М.М. Русинова. - Л.: Машиностроение. Ленинградское отд-ние, 1984, с.110] как:

П ' = ( 0 0 − 1 0 1 0 1 0 0 ) ,   П ' ' ( 0 0 1 0 1 0 − 1 0 0 )                                                     ( 6 )

Нестабильность пространственного положения пентапризмы приводит к повороту вектора N ¯ в рассматриваемой системе координат. Будем считать, что повороты происходят в следующей последовательности:

- вокруг оси OZ на угол α;

- вокруг новой оси OY' на угол β;

- вокруг новой оси OX'' на угол γ.

Соответствующие этим поворотам матрицы преобразования имеют следующий вид [Вычислительная оптика: Справочник / М.М. Русинов, А.П. Грамматин, П.Д. Иванов и др. Под общ. ред. М.М. Русинова. - Л.: Машиностроение. Ленинградское отд-ние, 1984, с.121]:

M z = ( cos α − sin α 0 sin α cos α 0 0 0 1 ) ;   M y = ( cos β 0 − sin β 0 1 0 sin β 0 cos β ) ; M x = ( 1 0 0 0 cos γ sin γ 0 − sin γ cos γ )   ( 7 )

Действие всех трех поворотов на произвольный вектор N ¯ описывается матрицей M:

M = M x ⋅ M y ⋅ M z                                                     ( 8 )

Пусть L → - вектор падающего на пентапризму луча, записанный в системе координат XYZ. Тогда вектор L → ' луча, преобразованного пентапризмой, пространственное положение которой имеет отступления от номинального, можно определить следующим образом:

L → ' = ( M ⋅ П ' ⋅ M − 1 ) ⋅ L → = T ⋅ L → ,                                                                   ( 9 )

где: T=M·П'·М^-1;

Будем считать, что углы поворота α, β, γ в схеме малы. Тогда с точностью до членов второго порядка малости по углам поворота, с учетом (7) и (8) можно записать выражения для M и M^-1:

M = ( 1 − sin α − sin β sin α 1 sin γ sin β − sin γ 1 ) = ( 1 − α − β α 1 γ β − γ 1 ) ,

M − 1 = ( 1 sin α sin β − sin α 1 − sin γ − sin β sin γ 1 ) = ( 1 α β − α 1 − γ − β γ 1 ) .

Отсюда следует, что

T = M ⋅ П ' ⋅ M − 1 = ( 0 − α − γ − 1 − α + γ 1 − α − γ 1 α − γ 0 )                                                                 ( 10 )

С учетом (9) и (10), на выходе из пентапризмы направление вектора L → ' будет определяться:

L → ' = ( 0 α − γ − 1 )                                                                                       ( 11 )

Этот вектор лежит в плоскости XOZ (т.е. перпендикулярен нормали луча на входе в пентапризму) и угол между осью OZ и этим лучом равен α-γ.

Используя полученные выражения, можно описать преобразование излучения лазера парой пентапризм, например, первой 1 и второй 2 пентапризмами, каждая из которых имеет свои случайные отклонения от номинального положения.

Вектор L → 0 (5) записан в системе координат X₀Y₀Z₀. Запишем вектор L → 1 , соответствующий вектору L → 0 , но уже в системе координат X₁Y₁Z₁, связанной с первой 1 пентапризмой первой пары пентапризм. Для этого используем известное выражение (7) для матрицы M_φ разворота системы координат вокруг оси OX на угол φ:

L → 1 = M φ ⋅ L → 0 = ( 1 0 0 0 cos φ sin φ 0 − sin φ cos φ ) ⋅ ( − 1 θ y θ z ) = = ( − 1 cos φ ⋅ θ y + sin φ ⋅ θ z − sin φ ⋅ θ y + cos φ ⋅ θ z ) = ( − 1 θ y ' θ z ' )                                                                         ( 12 )

В системе координат X₁Y₁Z₁ вектор луча L → 1 ' на выходе первой 1 пентапризмы с учетом (10) и (11) находим следующим образом:

L → 1 ' = T 1 ⋅ L → 1 = ( 0 − α 1 − γ 1 − 1 − α 1 + γ 1 1 − α 1 − γ 1 1 α 1 − γ 1 0 ) ( − 1 θ y ' θ z ' ) = ( − θ z ' − α 1 − γ 1 + θ y ' − 1 )

где: α₁, γ₁ - углы разворота первой призмы:

T 1 = ( 0 − α 1 − γ 1 − 1 − α 1 + γ 1 1 − α 1 − γ 1 1 α 1 − γ 1 0 ) .

Свяжем со второй 2 пентапризмой систему координат X₂Y₂Z₂ (см. рисунок 3a), ориентированную относительно самой призмы так же, как система координат X₁Y₁Z₁ ориентирована относительно первой 1 пентапризмы. Преобразуем вектор L → 1 ' в вектор L → 2 , записанный в системе координат X₂Y₂Z₂:

L → 2 = ( − 1 α 1 − γ 1 + θ y ' θ z ' )

Преобразование вектора L → 2 второй пентапризмой можно записать как:

L 2 ' → = T 2 ⋅ L 2 → = ( 0 − α 2 − γ 2 − 1 − α 2 + γ 2 1 − α 3 − γ 2 1 α 2 − γ 2 0 ) ( − 1 α 1 − γ 1 + θ y ' θ z ' ) = = ( − θ z ' ( α 1 − γ 1 ) + ( α 2 − γ 2 ) + θ y ' − 1 )

где: α₂, γ₂ - углы разворота второй призмы;

T 2 = ( 0 − α 2 − γ 2 − 1 − α 2 + γ 2 1 − α 2 − γ 2 1 α 2 − γ 2 0 ) .

Запишем этот вектор в системе координат X₁Y₁Z₁ (см. рисунок 3a):

L → 2 ' ∗ = ( 1 ( α 1 − γ 1 ) + ( α 2 − γ 2 ) + θ y ' − θ z ' )                                               ( 13 )

И, наконец, запишем его в системе координат X₀Y₀Z₀, используя матрицу разворота вокруг оси OX (7) на угол -φ. Таким образом, получаем искомый вектор L → n p луча на входе в приемную систему, записанный в системе координат X₀Y₀Z₀:

L n p → = M ( − ϕ ) L → 2 ' ∗ = ( 1 0 0 0 cos ( − ϕ ) sin ( − ϕ ) 0 − sin ( − ϕ ) cos ( − ϕ ) ) ⋅ ( 1 ω + θ y ' − θ z ' ) = = ( 1 ( ω + θ y ' ) cos ϕ + θ z ' ⋅ sin ϕ ( ω + θ y ' ) sin ϕ − θ z ' ⋅ cos ϕ ) = ( 1 θ y n p