Способ определения равномерного натяжения мембраны из изотропного материала

Способ определения равномерного натяжения мембраны из изотропного материала

Иллюстрации

Показать все

Реферат

Изобретение относится к измерительной технике и может использоваться для измерения натяжений мембранных элементов конструкций, таких как, например, отражающая поверхность крупногабаритного раскрываемого рефлектора, выполненная из металлического сетеполотна, натяжений биологических мембран и т.п.

В настоящее время разрабатываются и создаются космические спутниковые антенны с диаметрами апертуры, достигающими нескольких десятков метров. Отражающая поверхность таких антенн выполняется из текстильного металлического сетеполотна. Величина натяжения сетеполотна оказывает существенное влияние на отражающие характеристики антенны, в связи с чем важными являются вопросы измерения и регулировки натяжения сетеполотна на этапах сборки и наземной настройки антенны. Сетеполотно как элемент конструкции спутниковой антенны практически не имеет изгибной жесткости и может считаться мембраной. Предлагаемый способ измерения натяжения мембраны, основанный на ее локальном деформировании является простым, достаточно точным, и может быть использован для измерения натяжений не только элементов раскрываемых космических антенн, но и других мембранных элементов, таких как, например, биологические мембраны.

Известен способ измерения натяжения мембраны музыкального барабана [1]. На мембрану устанавливают опорное кольцо с закрепленным на нем индикатором часового типа. Индикатор закрепляют таким образом, что его ножка расположена в центре опорного кольца. При установке кольца на поверхность барабана пружина индикатора оказывается сжата. По степени сжатия пружины определяют величину натяжения мембраны.

Известен способ измерения натяжения поверхности сетки теннисной ракетки [2]. В сетчатую поверхность ракетки вдавливают с помощью гидравлического механизма индентор, имитируя воздействие теннисного мяча при ударе. Натяжение определяют по величине давления в гидравлическом механизме.

Наиболее близким к предлагаемому способу по технической реализации является способ определения натяжения мембранных элементов [3]. По этому способу производится несколько измерений величины прогиба мембраны под действием поперечной нагрузки при различных значениях силы вдавливания. По измеренным значениям строится кривая нагрузка-перемещение, которая затем сравнивается с аналогичной кривой (семейством кривых), полученной в результате численного расчета.

Недостатком данного способа является сложность методики, связанная с отсутствием прямого выражения для определения величины натяжения, а также с необходимостью проводить несколько измерений для определения постоянной величины натяжения.

Техническим результатом изобретения является разработка простого универсального способа определения равномерного натяжения мембраны, основанного на ее локальном деформировании.

Указанный технический результат достигается тем, что мембрану защемляют двумя кольцами, расположенными по разные стороны натянутой поверхности мембраны, к ней прикладывают поперечную нагрузку, распределенную по площади круга, центр которого совпадает с центрами защемляющих колец и измеряют прогиб. Величину равномерного натяжения мембраны σ⁽⁰⁾ вычисляют по формуле

σ ( 0 ) = P 2 I H π ;

I = ∫ d b [ B 2 [ 1 − 1 1 + H 2 B 2 ] − 1 r ∫ b r B 2 1 + H 2 B ​ 2 d r ] r d r ;

B = 4 b 2 r 2 ln r b + 2 b 2 ( d 2 + r 2 ) − 2 r 2 ( b 2 + d 2 ) r ( b 4 − d 4 + 4 b 2 d 2 ln d b ) .

Где σ⁽⁰⁾ - величина равномерного натяжения мембраны, Н/м;

Р - величина поперечной нагрузки (силы сопротивления), Н;

Н - величина максимального прогиба мембраны, м;

b - внутренний радиус защемляющих колец, м;

d - радиус круговой площадки, по которой распределена нагрузка, м;

r - переменная интегрирования, имеющая смысл радиальной координаты, м.

Приведенная формула для вычисления натяжения мембраны является решением следующей задачи: защемленная по краям круглая осесимметричная изотропная мембрана, имеющая значительное предварительное натяжение, изгибается силами, распределенными по площади круга малого радиуса, центр которого совпадает с центром мембраны. Решение этой задачи получено с использованием уравнения принципа виртуальной дополнительной работы, которое имеет вид

∭ V [ ( σ i j + σ i j ( 0 ) ) δ ε i j − ( P ¯ i + P ¯ i ( 0 ) ) δ u i ] d V − ∬ S 1 ( F ¯ i + F ¯ i ( 0 ) ) δ u i d S = 0 ,

где

ε_ij=(1/2)(u_i'j+u_j'i+u_k'iu_k'j).

Здесь V - объем, занимаемый телом,

S₁ - часть поверхности, на которой заданы внешние нагрузки,

σ i j ( 0 ) - начальные напряжения, вызванные предварительным натяжением,

σ_ij - добавочные напряжения, получаемые мембраной в результате приложения к ней нагрузки,

P ¯ i ( 0 ) , P ¯ i соответственно начальные и дополнительные массовые силы, отнесенные к единице объема,

F ¯ i ( 0 ) , F ¯ i - соответственно начальные и дополнительные поверхностные силы, отнесенные к единице площади поверхности,

u_i - перемещения.

ε_ij - деформации

δ - оператор варьирования.

Интегрируя уравнение принципа виртуальной дополнительной работы в предположении, что после приложения изгибающей нагрузки напряженное состояние натянутой мембраны не меняется, массовые силы отсутствуют, а также учитывая осевую симметрию задачи, получено выражение для определения начальных напряжений σ i j ( 0 ) , которое, будучи умноженным на толщину мембраны, даст приведенную формулу для величины натяжения мембраны. Также учтено, что натяжение мембраны - равномерное, т.е. главные напряжения равны друг другу [4, 5].

В результате сопоставления приведенной аналитической формулы с результатами нелинейного конечно-элементного анализа установлено, что максимальная точность измерений достигается, если выполняется условие 0,05≤d/b≤0,15, и величина нагрузки сопоставима с ожидаемой величиной натяжения мембраны.

Сущность изобретения поясняется чертежами

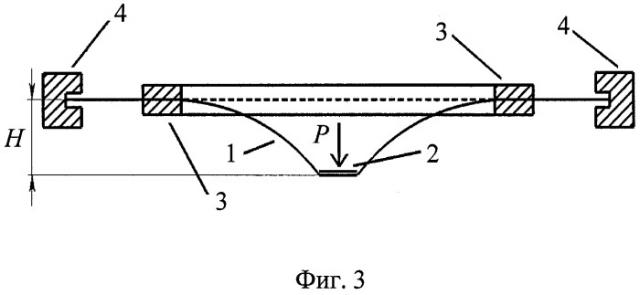
На Фиг.1 показан вид сверху расположения на мембране защемляющих колец и площадки приложения нагрузки: 1 - мембрана; 2 - площадка, по которой распределена нагрузка; 3 - защемляющие кольца; 4 - внешняя граница мембраны.

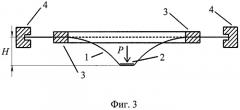
На Фиг.2 показан вид сбоку расположения на мембране защемляющих колец и площадки приложения нагрузки: 1 - мембрана; 2 - площадка, по которой распределена нагрузка; 3 - защемляющие кольца; 4 - внешняя граница мембраны.

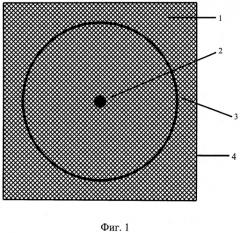
На Фиг.3 показано деформированное состояние мембраны после приложения нагрузки: 1 - мембрана; 2 - площадка, по которой распределена нагрузка; 3 - защемляющие кольца; 4 - внешняя граница мембраны.

В качестве примера практической реализации способа рассмотрим измерение натяжения металлического сетеполотна СМеТ-В15×2 (А+А) без покрытия. Сетеполотно натянуто на горизонтальную рамку размерами 25×25 см. Внутренний радиус защемляющих колец b=10 см. В центр области сетеполотна, заключенной внутри колец, вдавливают пластиковый диск радиусом d=1,5 см с усилием Р=5,50±0,25 гс (Фиг.1). Прогиб сетеполотна измеряют с помощью катетометра, прогиб составляет 0,314±0,015 см (Фиг.2). Коэффициент I определяют численно, I=0,429. Таким образом, измеренная величина равномерного натяжения сетеполотна составляет σ⁽⁰⁾=6,5 гс/см.

Достигаемый эффект составляют простота использования, точность результатов, возможность применять способ к различным конструкциям и материалам в широком диапазоне натяжений.

ЛИТЕРАТУРА

1. Patent JP 57037231 (A), Japan, G01L 5/04. Method and apparatus for measuring tension of musical instrument such as drum-head / Nagamatsu Masaaki; applicant Nagamatsu Masaaki. Publication date 1982.03.01

2. Patent US 4077256 (A), United States, G01L5/08. Stringed racket face tension measuring device / Hollander Bruce Lee; applicant Hollander Bruce Lee. Publication date 1978.03.07

3. Kazuo Tanizawa, Kazuo Yamamoto. Measuring apparatus for membrane tension and its characteristics // Theoretical and Applied Mechanics Japan. Vol.53 (2004) p.75

4. Васидзу, К. Вариационные методы в теории упругости и пластичности: Пер. с англ. М.: Мир, 1987. - 542 с.

5. Прочность, устойчивость, колебания. Справочник в трех томах. Т.1. М.: Машиностроение, 1968, - 831 с.

6. Вольмир, А.С. Гибкие пластинки и оболочки. М.: Государственное издательство технико-теоретической литературы, 1956. - 419 с.

Способ определения равномерного натяжения мембраны из изотропного материала, включающий защемление мембраны двумя кольцами, расположенными по разные стороны натянутой поверхности мембраны, приложение поперечной нагрузки, распределенной по площади круга, центр которого совпадает с центрами защемляющих колец и измерение максимального прогиба мембраны, отличающийся тем, что равномерное натяжение мембраны σ⁽⁰⁾ вычисляют по формуле: σ ( 0 ) = P 2 I H π ; I = ∫ d b [ B 2 [ 1 − 1 1 + H 2 B 2 ] − 1 r ∫ b r B 2 1 + H 2 B ​ 2 d r ] r d r ; B = 4 b 2 r 2 ln r b + 2 b 2 ( d 2 + r 2 ) − 2 r 2 ( b 2 + d 2 ) r ( b 4 − d 4 + 4 b 2 d 2 ln d b ) , где σ⁽⁰⁾ - величина равномерного натяжения мембраны, H/м;Р - величина поперечной нагрузки, H;Н - величина максимального прогиба мембраны, м;b - внутренний радиус защемляющих колец, м;d - радиус круговой площадки, по которой распределена нагрузка, м;r - переменная интегрирования, имеющая смысл радиальной координаты, м;причем радиус круговой площадки, по которой распределена нагрузка, и внутренний радиус защемляющих колец находятся в соотношении 0,05≤d/b≤0,15.