Способ тестопригодности реализации логических преобразователей

Способ тестопригодности реализации логических преобразователей

Иллюстрации

Показать все

Реферат

Изобретение относится к области автоматики и цифровой вычислительной техники и может быть использовано для создания сложных логических преобразователей (комбинационных автоматов) с самопроверкой правильности функционирования в рабочем режиме и высокой степенью готовности к оперативному динамическому функциональному тестированию при электронном переключении логических преобразователей из рабочего режима в режим тестирования.

Известен способ и вариант его технической реализации, обеспечивающий тестопригодность логических преобразователей, реализованных в виде двухуровневых программируемых логических матриц (ПЛМ), логическим базисом которых является основной элементный базис из логических элементов И, ИЛИ, НЕ [1].

ПЛМ содержит входной дешифратор «1→2», матрицу многовходовых элементов И, матрицу многовходовых элементов ИЛИ и дополнительные схемы, распределенные по узлам ПЛМ. Во входной дешифратор добавлены две линии управления; к столбцам матрицы И дополнительно подключаются выходы разрядов дополнительного регистра сдвига; в матрицу И и в матрицу ИЛИ дополнительно вводятся один столбец и одна строка соответственно, для дополнения до нечетности подключений к каждой строке и каждому столбцу; к строкам и столбцам дополнительно подключаются наборы из элементов неравнозначности (сумма по модулю 2). Линии управления, которые подключаются к дешифраторам, используются для активизации какой-либо одной или одновременно всех строк матрицы И. Дополнительный регистр сдвига предназначен для активизации какого-либо одного столбца матрицы, или всех столбцов одновременно. Если активизированы все строки матрицы и только один из столбцов, то проверяется правильность формирования 1-го терма (i-ой элементарной конъюнкции) путем проверки на нечетность числа переменных i-го терма дополнительным столбцом из последовательно включенных элементов неравнозначности. Если активизированы единственная строка матрицы и все ее столбцы, то проверяется на нечетность количество вхождений переменной данного типа в различные термы дополнительной строкой из последовательно соединенных элементов неравнозначности. Таким образом, данный способ тестирования двухуровневой ПЛМ заключается во введении такой структурной и функциональной избыточностей в двухуровневую ПЛМ, которая позволяет проводить последовательную проверку целостности структуры как незапрограммированной, так и запрограммированной ПЛМ путем предварительного обеспечения и последующего определения нечетности числа переменных в каждом терме (т.е. в каждом столбце матрицы) и нечетности вхождения каждой переменной в различные термы (т.е. в каждой строке матрицы), при этом реализуемая логическим преобразователем логическая функция исходно представляется и программируется в виде дизъюнктивной нормальной формы. Недостатками данного способа тестопригодной реализации логических преобразователей и устройств на его основе является невозможность проверки правильности функционирования логических преобразователей на предельных рабочих частотах, а также наличие значительного количества дополнительных узлов и коммутаций, приводящих к снижению общей надежности функционирования логических преобразователей.

Наиболее близким по технической сути является способ тестопригодной реализации логических преобразователей, описанный в [2].

Данный способ состоит в том, что он включает первоначальное получение исходного математического описания рабочего закона функционирования n-входовых логических преобразователей в тестопригодном логическом базисе Жегалкина, затем разработку и реализацию структурной схемы логического преобразователя из элемента генератор логической 1, r последовательных цепочек из (k-1) двухвходовых логических элементов с электронно перестраиваемой логической функцией, реализующих k-аргументные функции И в рабочем режиме или функции равнозначности в режиме тестирования, и последовательной цепочки из (r-1) двухвходовых элементов неравнозначности, реализующих рабочую функцию F_p путем свертки по модулю два всех k-аргументных конъюнкций, определение в последующем n тестовых М-последовательностей из одного и того же замкнутого класса и эталонной М-последовательности, которую алгоритмически формируют из n тестовых М-последовательностей, причем в режиме тестирования тестовые и эталонную М-последовательности одновременно генерируют внешним n-разрядным регистром сдвига с линейной обратной связью на предельно возможной рабочей частоте логического преобразователя.

Данный способ обеспечивает высокую тестопригодность логических преобразователей как для их статического, так и динамического тестирования на предельной рабочей частоте путем электронного переключения из рабочего режима в режим тестирования М-последовательностями. Однако данный способ не обеспечивает максимальной надежности функционирования логических преобразователей непосредственно в рабочем режиме.

Изобретение направлено на повышение надежности функционирования тестопригодных логических преобразователей путем придания им дополнительного свойства самопроверяемости в режиме работы.

Это достигается тем, что на этапе разработки и реализации структурной схемы логического преобразователя дополнительно вводят (s+1) последовательных цепочек из (k-1) двухвходовых логических элементов с электронно перестраиваемой логической функцией и последовательную цепочку из (s+1) двухвходовых элементов неравнозначности, которая на выходе формирует признак ошибки путем реализации свертки по модулю два значения функции F_p, всех s дополнительных k-аргументных конъюнкций и дополнительной n-аргументной конъюнкции инверсий входных аргументов, причем сумма s+r=2", то есть равна количеству всех различимых k-аргументных конъюнкций в полиноме Жегалкина общего вида, включая и единичную конъюнкцию.

Для осуществления предлагаемого изобретения закон функционирования n-входового логического преобразователя исходно должен быть задан полиномом Жегалкина, общий вид которого может быть представлен следующим образом:

F(x 1 , x 2 ,. … x n ) = C 0   ⊕ C 1 x 1   ⊕  C 2 x 2   ⊕ … ⊕  C n x n   ⊕  C (n + 1 )  x 1  x 2   ⊕  C (n + 2)  x 1  x 3   ⊕ … … ⊕  C (m-1) x 1 x 2 … x n ,                                                                                                                                          (1)

где х_i - i-ая входная логическая переменная;

C_j - j-ый коэффициент, указывающий на необходимость реализации соответствующей конъюнкции при C_j=1;

x_i x_f…x_g - некоторая k-аргументная конъюнкция логических переменных;

m=2ⁿ; C_j={0,1}, j=0, (2ⁿ-1); x_i={0,1}, i=1, n.

Сочетание переменных в правой части (1), например, C_(m-i) x₁ x₂…x_n, следует понимать как их логическое произведение (конъюнкцию), т.е.

С_(m-1)x₁…x₂…x_n=C_(m-1)&x₁&x₂&…&x_n

Запишем выражение (1) несколько иначе:

F(x 1 , x 2 ,. … x n ) = C 0 K 0   ⊕ C 1 K 1   ⊕ C 2 K 2   ⊕ … ⊕  C (m-1) K (m-1) ,                  (2)

где конъюнкция К₀=1 представляет единичную конъюнкцию.

Широко известно, что в выражении (2) все коэффициенты C_j будут равны 1 только в том случае, если реализуется логическая функция n-аргументной конъюнкции инверсий входных аргументов, то есть

x , 1 x , 2 … x , n = K 0   ⊕ K 1   ⊕ K 2   ⊕ … ⊕  K (m-1) ,                      (3)

где x_i следует понимать как инверсию х_i.

Тогда, в соответствии с законами алгебры логики относительно операции неравнозначности можно выражение (3) преобразовать к виду

K 0 ⊕ K 1 ⊕ K 2 ⊕ … ⊕  K (m-1)   ⊕  x , 1 x ' 2 … x ' n = 0                         (4)

В зависимости от того, какую именно логическую функцию должен реализовывать n-входовый логический преобразователь, предварительно определяют значения соответствующих коэффициентов С_j для логической функции (F_p), реализуемой в рабочем режиме, что может быть осуществлено широко известным методом неопределенных коэффициентов [3]. Тогда, как следует из выражения (4), если r конъюнкций, обеспечивающих реализацию рабочей функции F_p, оставить в левой части выражения (4), а оставшиеся (s+1) конъюнкций перенести в правую часть этого выражения, то они будут равны при любых значениях входных аргументов. Это обеспечивает самопроверяемость логических преобразователей в рабочем режиме функционирования путем использования дополнительной последовательной цепочки из (s+1) двухвходовых элементов неравнозначности, которая на выходе формирует признак ошибки путем реализации свертки по модулю два значения функции F_p, всех s дополнительных k-аргументных конъюнкций и дополнительной n-аргументной конъюнкции инверсий входных аргументов, причем сумма s+r=2ⁿ.

Рассмотрим осуществление заявляемого способа тестопригодной реализации логического преобразователя, рабочий закон функционирования которого изначально задается следующим полиномом Жегалкина:

F p  (x 1 , x 2 , x 3 ) = 1  ⊕  x 2   ⊕  x 1 x 3 ⊕  x 1  x 2  x 3 .                            (5)

В выражение (5) входят четыре конъюнкции, включая единичную конъюнкцию, то есть r=4. Основываясь на общем виде полинома Жегалкина для трех аргументов, находим s=4 отсутствующих в выражении (5) конъюнкций: x₁, x₃, x₁x₂, x₂x₃. Сформируем проверяющую функцию:

F np  (x 1 , x 2 , x 3 ) = x 1 ⊕  x ⊕ 3 x 1 x 2 ⊕  x 2 x 3 ⊕  x , 1 x , 2 x , 3            (6)

Сформируем сигнал ошибки Е, который примет единичное значение в том случае, если в режиме работы рабочая и проверяющая функции не совпадут

E = F p ⊕ F пp = 1 ⊕  x 2 ⊕ x 1 x 3 ⊕  x 1 x 2 x 3 ⊕ x 1 ⊕ x 3 ⊕  x 1 x 2 ⊕ x 2 x 3   ⊕ x , 1 x , 2 x , 3      (7)

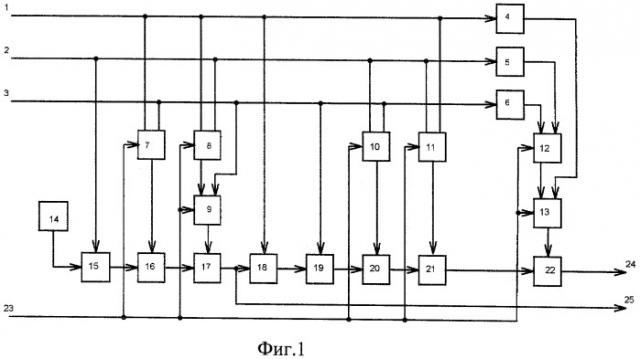
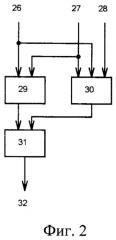
На фиг.1 представлена структурная схема самопроверяемого тестопригодного логического преобразователя, которая разработана на основе соотношений (5), (6) и (7), а на фиг.2 - структурная схема логического элемента VAR с электронно перестраиваемой логической функцией.

Входные логические переменные x₁, x₂, х₃ подаются соответственно на входы логического преобразователя 1, 2, 3. В соответствии с реализуемой логической функцией F_p (x₁, x₂, х₃) вход 1 подключаются к первому 26 входу элементов VAR 7, 8. Ко второму входу 27 элемента 7 подключается вход 3 логического преобразователя, а ко второму входу 27 элемента 8 подключается вход 2 преобразователя. Выход элемента 8 подключается к входу 26 элемента VAR 9, образуя, таким образом, их последовательную цепочку. Второй вход 27 элемента VAR 9 соединен со входом 3 логического преобразователя. На вход 23 поступает дополнительный сигнал управления u, который подключается к третьим входам 28 всех элементов VAR 7, 8, 9, 10, 11, 12, 13. Первые входы элементов неравнозначности 15, 16, 17 соответственно соединены с вторым входом логического преобразователя, с выходом элемента 7 и выходом элемента 9. Выходы элементов 15 и 16 соответственно соединяются со вторыми входами элементов 16 и 17. Второй вход элемента 15 соединен с выходом элемента 14, реализующего логическую функцию генератора логической 1. Выход элемента 17 соединен с выходом 25 логического преобразователя, где формируется логическая функция F_p (x₁, x₂, х₃) в рабочем режиме преобразователя. Элементы 15, 16, 17 образуют первую последовательную цепочку из трех (r-1) двухвходовых элементов неравнозначности, реализующих рабочую функцию F_p путем свертки по модулю два четырех (i=4) k-аргументных конъюнкций (включая нулевую конъюнкцию). Для обеспечения свойства самопроверяемости логического преобразователя в режиме работы, вводят дополнительную последовательную цепочку из пяти (s+1) двухвходовых элементов неравнозначности 18, 19, 20, 21, 22, которая на выходе 24 формирует признак ошибки путем реализации свертки по модулю два значения функции F_p, всех s=4 дополнительных k-аргументных конъюнкций и дополнительной n-аргументной конъюнкции инверсий входных аргументов, причем сумма s+r=2ⁿ, то есть равна количеству всех различимых k-аргументных конъюнкций в полиноме Жегалкина общего вида, включая и единичную конъюнкцию. Выходы элементов 18, 19, 20, 21 соответственно подключают к вторым входам элементов 19, 20, 21, 22, а выход элемента 22 подключают к выходу 24 преобразователя, образуя таким образом дополнительную последовательную цепочку из элементов неравнозначности. Первые входы элементов 18, 19, 20, 21, 22 соответственно соединены с входом 1 и входом 3 преобразователя, выходами элементов 10, 11 и 13. Второй вход элемента 18 подключен к выходу элемента 17 и выходу 25 логического преобразователя. Первые входы 26 элементов 10 и 11 подключены к входу 2 преобразователя, а вторые входы 27 элементов 10 и 11 соответственно подключены к входам 3 и 1 преобразователя. Входы инверторов 4, 5, 6 подключены соответственно к входам 1, 2, 3 логического преобразователя. Выход элемента 6 подключен к входу 26 элемента 12, второй вход которого подключен к выходу элемента 5. Выход элемента 12 подключен к входу 26 элемента 13, ко второму входу 27 которого подключен выход элемента 4.

При u=1, реализуется рабочий режим функционирования логического преобразователя в соответствии с заданной логической функцией (в данном случае, F_p), что обеспечивается настройкой всех элементов VAR 7, 8, 9, 10, 11, 12, 13 на последовательную реализацию конъюнкций переменных, поступающих на их входы 26 и 27. В таблице показаны значения функций F_p (5) и F_np (6) в рабочем режиме функционирования.

Таблица
x1	0	1	0	1	0	1	0	1
x2	0	0	1	1	0	0	1	1
х3	0	0	0	0	1	1	1	1
Fp	1	1	0	0	1	0	0	0
Fпр	1	1	0	0	1	0	0	0

Как видно из представленной таблицы, на всех возможных наборах входных переменных при правильно функционирующем логическом преобразователе значения функций F_p и F_пp должны совпадать, что и обеспечивает придание свойства самопроверяемости тестопригодным логическим преобразователям в рабочем режиме функционирования.

При u=0 структура логического преобразователя реконфигурируется путем одновременной электронной перестройки элементов 7, 8, 9, 10, 11, 12, 13 на реализацию логической функции равнозначности (⊗) над логическими переменными, поступающими на их входы 26 и 27. Логическое уравнение, задающее закон функционирования элементов 7, 8, 9, 10, 11, 12, 13 при поступлении на их входы 26 и 27 переменных а и b соответственно и на вход 28 сигнала управления u, имеет следующий вид:

y = (a & b) + (a + b + u) ¯                         (8)

где y - выходной сигнал, формируемый на выходах 32 элементов 7, 8, 9, 10, 11, 12,13, в которых элемент 29 реализует логическую функцию И над входными сигналами a и b, элемент 30 реализует логическую функцию ИЛИ-НЕ над сигналами a и b, а также над сигналом управления u, а элемент 31 реализует функцию ИЛИ над сигналами с выходов элементов 29 и 30. В результате настройки элементов 7, 8, 9, 10, 11, 12, 13 на реализацию функции равнозначности, функции F_p и F_пp преобразуются, так как в соответствующих им уравнениях все конъюнкции будут заменены на операции равнозначности. Такие уравнения получают из исходного математического описания путем формальной замены в нем всех операций логического И на операции равнозначности с последующим приведением их к операциям неравнозначности.

В зависимости от реализуемой логической функции в рабочем режиме, логический преобразователь в режиме тестирования (при отсутствии в нем неисправностей) реализует одну из возможных линейных логических функций, общий вид которых соответствует соотношению (9):

F*(x 1 , x 2 ,. … x n ) = B 0   ⊕ B 1 x 1   ⊕  B 2 x 2   ⊕ … ⊕  B n-1 x n-1      (9)

где коэффициенты В₁={0,1}, i=0, n-1; x_j={0,1}, j=1, n.

Коэффициенты B_i не вычисляются, они автоматически находятся из выражений вида (5), с использованием соотношений (10):

x i ⊗   x j = 1  ⊕  x i   ⊕  x j ;    x i   ⊕  x i = 0;    x i   ⊕  x i   ⊕  x i = x i .        (10)

С учетом (9) и (10) в режиме тестирования функции F_p (5) и F_пp (6) приводятся к виду:

F* p (x 1 , x 2 ,. … x n ) = 1  ⊕  x 2 ⊕ x 1 ⊗ x 3 ⊕  x 1 ⊗ x 2 ⊗ x 3 = 0 ,   (11) 

F* пр (x 1 , x 2 ,x 3 ) = x 1   ⊕  x 3   ⊕ x 1 ⊕ x 2 ⊕ x 2 ⊗ x 3   ⊕  (x , 1 ⊗  x . 2   ⊕  x , 3 ) = ( x 1 ⊗  x 2 ⊕ x 2 ) ,   ( 12)

В режиме тестирования логического преобразователя переменные х_j (j=1, n) заменяются на псевдослучайные последовательности максимальной длины (М-последовательности), которые могут генерироваться на предельных частотах внешним n-разрядным регистром сдвига с линейной обратной связью [4]. Множество М всех М-последовательностей, генерируемых n-разрядным регистром сдвига, состоит из 2(2ⁿ-1) М-последовательностей, отличающихся друг от друга величиной циклического сдвига и/или инверсными значениями битовых сигналов. Тогда каждой М-последовательности можно присвоить номер, соответствующий ее циклическому сдвигу, относительно какой-либо М-последовательности, произвольно выбранной за первую. Тогда М={M₁, M₂,.…M_S}, S=2(2ⁿ-1). Специфической особенностью M_S из М является то, что для них выполняются все соотношения (10), при этом эталонная реакция М_Э правильно функционирующего логического преобразователя будет также принадлежать множеству М и может алгоритмически формироваться из n тестовых М-последовательностей, что обеспечивает возможность одновременного формирования тестовых и эталонной М-последовательностей на предельной рабочей частоте логического преобразователя. Как видно из структурной схемы, представленной на фиг.1, и соотношений (10), любая константная неисправность, кроме неисправностей на входах, будет искажать выходную функцию логического преобразователя в режиме тестирования М-последовательностями и, следовательно будет обнаружена при несовпадении выходного сигнала логического преобразователя с М_Э. Так же эффективно обнаруживаются неисправности типа короткие замыкания. При коротких замыканиях проводников в цифровой схеме в точках замыкания реализуются над логическими (двоичными) сигналами, так называемые монтажное И или монтажное ИЛИ. Если электрический сигнал логического 0 подавляет электрический сигнал логической 1, то реализуется монтажное И. Если электрический сигнал логической 1 подавляет электрический сигнал логического 0, то реализуется монтажное ИЛИ. С учетом этого, а также уникальной особенности М-последовательностей, заключающейся в том, что любые две различные М-последовательности из одного того же класса отличаются в половине своих (2ⁿ-1) разрядах, следует, что любые неисправности типа коротких замыканий будут обнаруживаться, так как при возникновении монтажных И или ИЛИ выходная функция логического преобразователя будет отличной от М_Э. Достоверное тестирование по данному способу необходимо проводить путем сравнения эталонного тестового сигнала с реально формируемым на выходе логического преобразователя с запаздыванием, величина которого определяется как τ=r t_ЗП, где r - количество последовательно включенных элементов неравнозначности, а t_ЗП - время задержки их переключения. Так же следует проверять признак ошибки в рабочем режиме функционирования логического преобразователя.

Техническим результатом от использования заявляемого изобретения является повышение надежности функционирования тестопригодных логических преобразователей путем придания им дополнительного свойства самопроверяемости в режиме работы.

Источники информации

1. Киносита К., Асада К., Карапу О. Логическое проектирование СБИС. - М.: Мир, 1988. - 309 с.

2. Патент RU 2413282 С2, МПК⁶ G06F 11/26. Способ тестопригодной реализации логических преобразователей / Акинина Ю.С. (RU), Подвальный С.Л. (RU), Тюрин С.В. (RU), заявитель и патентообладатель ГОУ ВПО «Воронежский госуд. техн. ун-т. (RU) - №2008151028/08; заявл. 22.12.2008; опубл. 27.02.2011, бюл. №6.

3. Гаврилов Г.Л., Сапоженко А.А. Задачи и упражнения по дискретной математике. - М.: Физматлит, 2005. - 460 с.

4. Ярмолик В.Н. Контроль и диагностика цифровых узлов ЭВМ. - Мн.: Наука и техника, 1988. - 240 с.

Способ тестопригодной реализации логических преобразователей, включающий первоначальное получение исходного математического описания рабочего закона функционирования n-входовых логических преобразователей в тестопригодном логическом базисе Жегалкина, затем разработку и реализацию структурной схемы логического преобразователя из элемента - генератор логической 1, r последовательных цепочек из (k-1) двухвходовых логических элементов с электронно перестраиваемой логической функцией, реализующих k-аргументные функции И в рабочем режиме или функции равнозначности в режиме тестирования, и последовательной цепочки из (r-1) двухвходовых элементов неравнозначности, реализующих рабочую функцию F_p путем свертки по модулю два всех k-аргументных конъюнкций, определение в последующем n тестовых М-последовательностей из одного и того же замкнутого класса и эталонной М-последовательности, которую алгоритмически формируют из n тестовых М-последовательностей, причем в режиме тестирования тестовые и эталонную М-последовательности одновременно генерируют внешним n-разрядным регистром сдвига с линейной обратной связью на предельно возможной рабочей частоте логического преобразователя, отличающийся тем, что на этапе разработки и реализации структурной схемы логического преобразователя дополнительно вводят (s+1) последовательных цепочек из (k-1) двухвходовых логических элементов с электронно перестраиваемой логической функцией и последовательную цепочку из (s+1) двухвходовых элементов неравнозначности, которая на выходе формирует признак ошибки путем реализации свертки по модулю два значения функции F_p, всех s дополнительных k-аргументных конъюнкций и дополнительной n-аргументной конъюнкции инверсий входных аргументов, причем сумма s+r=2ⁿ, то есть равна количеству всех различимых k-аргументных конъюнкций в полиноме Жегалкина общего вида, включая и единичную конъюнкцию.