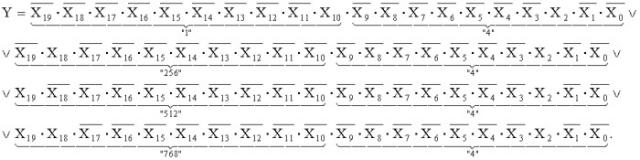Способ цифроаналогового преобразования

Способ цифроаналогового преобразования

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение.

Изобретение относится к измерительной технике, автоматике, а также к технике преобразования цифровых величин в аналоговые, может быть использовано при создании высокоточных аналого-цифровых преобразователей и систем контроля параметров изделий электронной техники.

Уровень техники.

Известны различные способы цифроаналогового преобразования [1], основанные на суммировании весовых токов или напряжений, полученных на базе управляемых кодом резистивных матриц различного типа, а также, например, на основе преобразования частоты в напряжение (см. [1], микросхема цифроаналогового преобразователя (ЦАП) КР1108ПП1, стр.257).

К недостаткам способов первого типа можно отнести технологическую сложность и дороговизну изготовления резистивных матриц, а второго - недостаточную точность и линейность характеристики преобразования. Известно - прецизионные резистивные матрицы можно изготовить только по тонкопленочной технологии, включающей функциональную подгонку сопротивлений резисторов, а не по полупроводниковой, что и определяет указанные недостатки.

Известен способ цифроаналогового преобразования [2], включающий получение импульсного ШИМ-сигнала, период которого определяется разрядностью преобразуемого кода и частотой задающего генератора, а скважность обратно пропорциональна преобразуемому коду, нормирование амплитуды полученного сигнала и последующую его фильтрацию в области нижних частот, при этом перед фильтрацией выполняют амплитудную модуляцию ШИМ-сигнала нормированным по амплитуде прямоугольным модулированным сигналом на частоте задающего генератора, причем в одном из полупериодов модулируемого сигнала на информационном интервале преобразования осуществляют запоминание предыдущего значения промежуточного преобразования.

Для реализации данного способа преобразования многоразрядного цифрового кода в величину напряжения или тока с высокой точностью требуется несколько высокостабильных и точных аналоговых узлов, например, таких как двухполярный источник опорного напряжения (тока), аналоговый сумматор, а нормированный по амплитуде модулированный сигнал можно создать лишь в результате прецизионной операции. Все это усложняет реализацию способа [2] и делает дорогим его воплощение.

Известен способ цифроаналогового преобразования с широтно-импульсной модуляцией (ШИМ), приведенный, например, в работах [3, 4] (прототип).

К недостаткам можно отнести большое время преобразования ЦАП, построенного на основании этого способа, а также существенную нелинейность характеристики преобразования.

Сущность изобретения.

Задачей, на которую направлено изобретение, является создание способа цифроаналогового преобразования, позволяющего выполнить это преобразование с заданной точностью за более короткое время.

Поставленная задача достигается за счет того, что в способе цифроаналогового преобразования, включающем получение импульсного сигнала, длительность цикла преобразования которого определяется разрядностью преобразуемого кода, а длительность информационного сигнала пропорциональна преобразуемому коду, последующие нормирование амплитуды полученного сигнала и его фильтрацию в области нижних частот, дополнительно, перед фильтрацией, информационный сигнал формируют в виде последовательности импульсов, дискретно-равномерно расположенных на временной оси в интервале цикла преобразования с их длительностью, кратной периоду колебаний тактового генератора, причем суммарная длительность этих импульсов в цикле преобразования пропорциональна преобразуемому коду.

Перечень фигур чертежей.

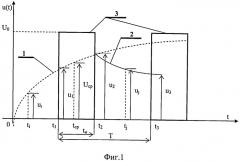
На фиг.1 представлены эпюры напряжений на входе и выходе фильтра нижних частот (ФНЧ), являющегося оконечным устройством цифроаналогового преобразователя. ФНЧ может собой представлять простейшую RC-цепочку. На позиции 1 представлена изменяющаяся во времени эпюра напряжений при накоплении емкостью конденсатора заряда;

на позиции 2 - эпюра разряда конденсатора; на позиции 3 - временная диаграмма импульсов, поступающих на вход ФНЧ, длительность которых является информационным параметром.

На эпюрах фиг.1 обозначены следующие параметры при заряде выходного конденсатора ФНЧ: u₁;, соответствующее времени t_i - мгновенное значение напряжения на выходе ФНЧ; u₁, соответствующее времени t_i (момент начала поступающего на ФНЧ импульса); U_cp - среднее значение выходного напряжения, соответствующее условному моменту времени t_cp; из, соответствующее времени t₂ (момент окончания поступающего на ФНЧ-импульса).

На эпюрах фиг.1 также обозначены временные параметры: Т - длительность цикла преобразования, t_и - длительность поступающего на ФНЧ-импульса; а также следующие параметры (эпюра 2) при разряде выходного конденсатора ФНЧ: u_j, соответствующее времени t_j - мгновенное значение напряжения на выходе ФНЧ, u₃ - напряжение, остающееся на конденсаторе ФНЧ в момент окончания цикла преобразования.

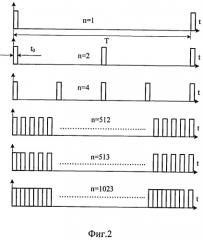
На фиг.2 представлены временные диаграммы поступающих на вход ФНЧ-импульсов напряжения в цикле преобразования Т при преобразовании десятиразрядных двоичных кодов N, соответствующих десятичным числам n: n=1, n=2, n=4, n=512, n=513, n=1023.

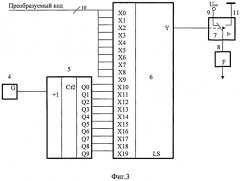
На фиг.3 представлена функциональная схема цифроаналогового преобразователя, реализующего предложенный способ. ЦАП содержит задающий тактовый генератор 4, двоичный счетчик 5, логическую комбинационную схему 6, управляемый аналоговый переключатель 7, фильтр нижних частот (ФНЧ) 8, клемму 9 подключения опорного напряжения, клемму 11 подключения шины нулевого потенциала.

Отличительные признаки.

Отличительными признаками заявленного способа по сравнению со способом-прототипом являются:

1. На интервале цикла преобразования Т дискретно-равномерно размещают n импульсов напряжения с амплитудой, равной опорному напряжению, и образцовой длительностью.

2. Число n соответствует преобразуемому двоичному коду N в десятичном выражении.

Сведения, подтверждающие возможность осуществления.

Сущность изобретения поясняется чертежами фиг.1÷3.

На фиг.1 представлены эпюры напряжений для классического ШИМ цифроаналогового преобразования, что соответствует прототипу [3, 4]. В этом случае

t и = t 2 − t 1 = n ⋅ t 0 ,                 ( 1 )

где t₀ - образцовый интервал времени, равный длительности периода импульсов задающего (тактового) генератора, n - десятичный эквивалент преобразуемого двоичного кода N. Скважность импульсов Q, согласно фиг.1, можно определить как

Q = T / t 0 n = n max n ,                 ( 2 )

где n_max - максимальное десятичное число, соответствующее максимальному преобразуемому двоичному коду N_max. В свою очередь, среднее значение напряжения U_ср определяется числом n, а число n_max является эквивалентом величины опорного напряжения U_о, тогда

U с р = U о Q ,                       ( 3 )

Мгновенное значение напряжения u_j на экспоненте 1 в момент времени t_i, фиг.1, определяется известным из курса электротехники выражением:

u i = U о ⋅ ( 1 − e − t 1 τ ) ,                 ( 4 )

где τ - постоянная времени фильтра ФНЧ, е - основание натурального логарифма.

Полагая, что u_j=U_ср, а также учитывая (2) и (3), получим:

U с р = U о ⋅ n T / t 0 = U о ⋅ ( 1 − e − t с р τ ) , откуда t с р = − τ ⋅ ln ( 1 − n T / t 0 ) = − τ ⋅ ln ( 1 − 1 Q ) .     ( 5 )

Можно выбрать значение напряжения U_ср как некоторую опорную точку на шкале выходных напряжений, относительно которой определяются значения u₁ и u₂.

Момент времени t₁ (момент начала импульса) наступает раньше момента t_ср на величину t_и/2=n·t₀/2, а момент времени t₂ (момент окончания импульса) наступает позже момента t_ср на n·t₀/2. Следовательно, с учетом (4) можно записать:

u 1 = U 0 ⋅ ( 1 − e − t n ˜ ∂ − n ⋅ t 0 / 2 τ ) ,                     ( 6 )

u 2 = U 0 ⋅ ( 1 − e − t n ˜ ∂ + n ⋅ t 0 / 2 τ ) ,                     ( 7 )

u 2 − u 1 = U 0 ⋅ ( 1 − e − t n ˜ ∂ − n ⋅ t 0 / 2 τ − e − t n ˜ ∂ + n ⋅ t 0 / 2 τ ) .         ( 8 )

Мгновенное значение напряжения u_j на экспоненте разряда (фиг.1, кривая 2) определяется выражением:

u j = u 2 ⋅ e − t j τ ,                                 ( 9 )

где t_j отсчитывается от момента времени t₂. При этом длительность разряда будет равна t₃-t₂=Т-n·t₀. Тогда с учетом (9) получим:

u 3 = u ⋅ 2 e − T − n ⋅ t 0 / n max τ .                     ( 10 )

При установившемся режиме должны соблюдаться равенства:

u 2 − u 3 = u 2 − u 1   и   u 3 = u 1 .             ( 11 )

Если во время классического ШИМ, преобразования десятичный эквивалент n преобразуемого кода мал (большое значение Q), то длительность заряда мала, однако скорость заряда при этом велика, так как разность напряжений U₀-u₁, под действием которой происходит заряд, велика. Скорость же разряда под действием разности напряжений u₂-u₁, наоборот, в этом случае будет небольшой ввиду малости этой разницы.

При маленьких значениях Q (n велико) все будет наоборот.

Также является известным фактом (см., например, [5]), что максимальное значение погрешности характеристики преобразования для ЦАП с ШИМ находится посредине шкалы преобразования. Это в свою очередь означает, что максимальный размах колебаний выходного напряжения фильтра u₂-u₁ должен быть в установившемся режиме при t_и=Т/2.

Для соблюдения необходимой точности преобразования нужно выбрать значение τ фильтра таким образом, чтобы максимальная амплитуда колебаний напряжения на его выходе u₂-u₁ не превышала бы двух квантов преобразования: u₂-u₁=2U_о/n_max, величина u₁ была бы на квант меньше U_ср, а величина u₂ была бы на квант больше U_ср.

Тогда u 1 = U 0 ⋅ n ⋅ t 0 T − U 0 n max = U 0 ( n ⋅ t 0 T − 1 n max ) = U 0 ( n n max − 1 n max ) = U 0 n − 1 n max

Выведем формулу расчета τ, подставив полученное значение u₁ в (6) и произведя преобразования с учетом (5):

u 1 = U 0 n − 1 n max = U 0 ⋅ ( 1 − e − t n ˜ ∂ − n ⋅ t 0 / 2 τ ) , 1 − n − 1 n max = e − t n ˜ ∂ − n ⋅ t 0 / 2 τ , ln n max − n + 1 n max = − t n ˜ ∂ − n ⋅ t 0 / 2 τ , ln n max − n + 1 n max = − − τ ⋅ ln ( 1 − n T / t 0 ) − n ⋅ t 0 / 2 τ , ln n max − n + 1 n max = ln ( 1 − n n max ) + n ⋅ t 0 2 ⋅ τ , ln n max − n + 1 n max − ln ( 1 − n n max ) = n ⋅ t 0 2 ⋅ τ , ln n max − n + 1 n max 1 − n n max = n ⋅ t 0 2 ⋅ τ , ln n max − n + 1 n max − n = n ⋅ t 0 2 ⋅ τ ,

τ = n ⋅ t 0 2 ⋅ ln n max − n + 1 n max − n ,

τ t 0 = n 2 ⋅ ln n max − n + 1 n max − n       ( 12 ) .

Проведем расчеты описанных параметров для конкретного ЦАП с ШИМ, условно приняв следующие безразмерные значения: t₀=1, Т=n_max=1024, n=512, U_о=10,24.

В этом случае согласно (12) получим: τ=128,125·Т≈128Т.

Расчеты остальных параметров такого ЦАП с ШИМ для некоторых кодов, имеющих соответствующие десятичные эквиваленты n, сведены в табл.1.

Таблица 1
n	Uср	tср	u1	u2	u3	u2-u1
1	0,01	128	0,0099609	0,0010039	0,0099609	0,000078
16	0,16	2064	0,159385	0,160615	0,159385	0,001230
256	2,56	37707	2,552495	2,567494	2,552495	0,01499999
512	5,12	90852	5,109987	5,129987	5,109987	0,02000001
768	7,68	181704	7,672486	7,687487	7,672486	0,0150000
1008	10,08	545113	10,079383	10,080613	10,079383	0,0012305
1023	10,23	908521	10,229960	10,230039	10,229960	0,000078

Данная расчетная табл.1 характеризует свойства ЦАП (в том числе размах пульсаций выходного напряжения u₂-u₁), реализующего способ цифроаналогового преобразования, принятый за прототип.

Чем больше величина пульсаций на выходе ФНЧ, тем больше погрешность преобразования ЦАП, а правая колонка табл.1 подтверждает параболический характер этой погрешности, указанной как нелинейность в работе [5].

В предложенном способе цифроаналогового преобразования не формируют ШИМ-импульс длительностью n·t₀, a n импульсов длительностью t₀ размещают дискретно-равномерно на интервале цикла преобразования Т. «Дискретно-равномерно» - нестандартный термин, призванный обозначить, что импульсы длительностью t₀ могут появиться только на целочисленных позициях счета тактов задающего генератора, начиная от начала цикла преобразования Т. Подобное распределение нормированных по амплитуде U_о и длительности t₀ на интервале Т импульсов показано на фиг.2 временными диаграммами при различных значениях преобразуемых кодов и различных, соответствующих этим кодам, десятичным эквивалентам n=1, 2, 4, 512, 513, 1023.

Согласно временным диаграммам при n=1 скважность Q = T t 0 , при n=2 скважность Q = T / 2 t 0 = T 2 ⋅ t 0 , при n=4 скважность Q = T / 4 t 0 = T 4 ⋅ t 0 и так далее, то есть Q = T n ⋅ t 0 . Таким образом, формула для определения скважности осталась прежней (2).

Так как в предложенном способе длительность одного импульса всегда равна t₀, то в формулах (6÷8) исчезает индекс n и эти формулы для расчета u₁, u₂, u₂-u₁ принимают следующий вид:

u 1 = U о ⋅ ( 1 − e − t с р − t 0 / 2 i τ ) ,                   ( 13 )

u 2 = U о ⋅ ( 1 − e − t с р + t 0 / 2 i τ ) ,                   ( 14 )

u 2 − u 1 = U о ⋅ ( e − t с р − t 0 / 2 i τ − e − t с р + t 0 / 2 i τ ) .       ( 15 )

Длительность же разряда в новом способе равна t₃-t₂=Т/n-t₀. Тогда с учетом (10) получим:

u 3 = u 2 ⋅ e − T / n − t 0 τ ,                         ( 16 )

Выведем формулу расчета τ учитывая, что величина u₁ должна быть на квант меньше U_ср, а величина u₂ - на квант больше U_ср:

u 1 = U 0 ⋅ n ⋅ t 0 T − U 0 n max = U 0 ( n ⋅ t 0 T − 1 n max ) = U 0 ( n n max − 1 n max ) = U 0 n − 1 n max . Подставляем это значение в (13) и производим преобразования:

u 1 = U 0 n − 1 n max = U 0 ⋅ ( 1 − e − t n ˜ ∂ − n ⋅ t 0 / 2 τ ) , 1 − n − 1 n max = e − t n ˜ ∂ − n ⋅ t 0 / 2 τ , ln n max − n + 1 n max = − t n ˜ ∂ − t 0 / 2 τ , ln n max − n + 1 n max = − − τ ⋅ ln ( 1 − n T / t 0 ) + t 0 / 2 τ , ln n max − n + 1 n max = ln ( 1 − n n max ) + t 0 2 ⋅ τ , ln n max − n + 1 n max − ln ( 1 − n n max ) = t 0 2 ⋅ τ , ln n max − n + 1 n max 1 − n n max = t 0 2 ⋅ τ , ln n max − n + 1 n max − n = t 0 2 ⋅ τ ,

τ = t 0 2 ⋅ ln n max − n + 1 n max − n ,

τ t 0 = 1 2 ⋅ ln N − n + 1 N − n       ( 16 ) .

Данная функция (16) имеет максимум при n=1.

Проведем расчеты описанных параметров для конкретного ПАП, условно приняв следующие безразмерные значения: t₀=1, Т=n_max=1024, n=7, U_о=10,24.

В этом случае, согласно (16) получим: τ=0,5·Т.

Расчеты остальных параметров ЦАП, реализующего предложенный способ, для некоторых кодов, имеющих соответствующие десятичные эквиваленты n сведены в табл.2.

Таблица 2
n	Uср	tср	u1	u2	U3	u2-u1
1	0,01	0,5	0,0000049	0,0199853	0,002710	0,019980
16	0,16	8,063	0,150151	0,169839	0,150175	0,0196875
256	2,56	147,29	2,552495	2,567495	2,552495	0,014999
512	5,12	354,89	5,114995	5,124995	5,114995	0,010000
768	7,68	709,78	7,767496	7,682496	7,767496	0,005000
1008	10,08	2129	10,07984	10,08016	10,07984	0,000312
1023	10,23	3548	10,22999	10,23000	10,22999	0,00005

Сравнивая значения параметров в таблицах 1 и 2 для смоделированных ЦАП, реализующих в первом случае способ-прототип, а во втором заявленный способ, при одинаковой разрядности моделируемых ЦАП, можно заключить: предложенный способ преобразования при одинаковой величине пульсации на выходе фильтра позволяет значительно уменьшить τ фильтра а, следовательно, повысить быстродействие всего устройства (в данном примере в 256 раз).

Следует заметить, что в предложенном способе максимум пульсаций выходного напряжения фильтра монотонно смещается в начало диапазона преобразования, так как там длительность разряда (паузы) возрастает до наибольшего значения, в то время как в известном способе максимум пульсаций выходного напряжения фильтра находится в середине шкалы преобразования.

Физическая реализация устройства может собой представлять логическую схему LS с одним выходом Y, подсоединенным к управляющему входу электронного аналогового переключателя, переключающего вход фильтра F между опорным напряжением и шиной нулевого потенциала, и 2·К входами, причем на первые К входов поступает преобразуемый двоичный код, а вторые К входов подключены к выходам K-разрядного двоичного счетчика импульсов Ст2, подсчитывающего импульсы тактового генератора G. Логическая схема LS реализует логическую функцию 2К переменных.

Конкретная схема 10-разрядного ЦАП (К=10) с предлагаемым способом преобразования представлена на фиг.3.

В качестве примера запишем функцию LS для входного кода «4» (в десятичной записи), при поступлении которого импульс на выходе должен появляться в 1, 256, 512 и 768 тактах распределенных на интервале цикла преобразования Т:

Y = X 19 ¯ ⋅ X 18 ¯ ⋅ X 17 ¯ ⋅ X 16 ¯ ⋅ X 15 ¯ ⋅ X 14 ¯ ⋅ X 13 ¯ ⋅ X 12 ¯ ⋅ X 11 ¯ ⋅ X 10 ︸ " 1 " ⋅ X 9 ¯ ⋅ X 8 ¯ ⋅ X 7 ¯ ⋅ X 6 ¯ ⋅ X 5 ¯ ⋅ X 4 ¯ ⋅ X 3 ¯ ⋅ X 2 ⋅ X 1 ¯ ⋅ X 0 ¯ ︸ " 4 " ∨ ∨ X 19 ¯ ⋅ X 18 ⋅ X 17 ¯ ⋅ X 16 ¯ ⋅ X 15 ¯ ⋅ X 14 ¯ ⋅ X 13 ¯ ⋅ X 12 ¯ ⋅ X 11 ¯ ⋅ X 10 ¯ ︸ " 256 " ⋅ X 9 ¯ ⋅ X 8 ¯ ⋅ X 7 ¯ ⋅ X 6 ¯ ⋅ X 5 ¯ ⋅ X 4 ¯ ⋅ X 3 ¯ ⋅ X 2 ⋅ X 1 ¯ ⋅ X 0 ¯ ︸ " 4 " ∨ ∨ X 19 ⋅ X 18 ¯ ⋅ X 17 ¯ ⋅ X 16 ¯ ⋅ X 15 ¯ ⋅ X 14 ¯ ⋅ X 13 ¯ ⋅ X 12 ¯ ⋅ X 11 ¯ ⋅ X 10 ¯ ︸ " 512 " ⋅ X 9 ¯ ⋅ X 8 ¯ ⋅ X 7 ¯ ⋅ X 6 ¯ ⋅ X 5 ¯ ⋅ X 4 ¯ ⋅ X 3 ¯ ⋅ X 2 ⋅ X 1 ¯ ⋅ X 0 ¯ ︸ " 4 " ∨ ∨