Способ определения параметров движения искусственного спутника земли по измерениям текущих навигационных параметров на коротком мерном интервале

Способ определения параметров движения искусственного спутника земли по измерениям текущих навигационных параметров на коротком мерном интервале

Иллюстрации

Показать все

Реферат

Изобретение относится к области определения параметров движения искусственного спутника Земли (ИСЗ) по результатам проведения измерений текущих навигационных параметров (ИТНП) на коротком мерном интервале, может быть использовано в автоматизированных системах навигационно-баллистического обеспечения (НБО) в условиях неполной реализации штатной схемы проведения радиоконтроля орбиты (РКО).

Известны способы определения параметров движения ИСЗ по результатам проведения ИТНП [1, 2], которые базируются на технологии построения обратного оператора G^-1, реализующего отображение пространства измерений на пространство определяемых параметров.

где G=А^ТРА, Δq - вектор поправок в уточняемые параметры движения ИСЗ;

А - матрица частных производных от измеряемых параметров по уточняемым;

Δh=h_ист+δh-h_paсч, h_ист - вектор истинных значений ИТНП;

δh - вектор ошибок в значениях ИТНП;

h_расч - вектор расчетных значений ИТНП.

В условиях реализации схемы проведения ИТНП на коротком мерном интервале матрица А близка к вырожденной и реализация отображения пространства измерений на пространство определяемых параметров может содержать ошибки превышающие допустимые значения. Решаемая задача в указанных условиях относится к классу некорректных задач определения параметров движения ИСЗ, когда решение является неустойчивым по отношению к ошибкам в векторе ИТНП. Это проявляется в том, что допустимым с точки зрения требований эксплуатационно-технической документации (ЭТД) ошибкам в ИТНП соответствуют недопустимые, согласно требований ЭТД, ошибки в векторе уточняемых параметров. Известный способ, применяемый при этих условиях [2], содержит процедуры декомпозиции задачи (1), базирующиеся на таких преобразованиях оператора G^-1, которые позволяют получить пробные решения (2) задач, квазиэквивалентных задаче (1)

и из них выбрать оптимальное.

Недостатком известного способа является отсутствие типовой технологии автоматизированного отбора пробных решений, которые обеспечивают выполнение условия корректности, когда допустимым с точки зрения требований эксплуатационно-технической документации (ЭТД) ошибкам в ИТНП соответствуют допустимые, согласно требований ЭТД, ошибки в векторе уточняемых параметров.

Целью изобретения - повышение точности и оперативности позиционирования ИСЗ за счет обеспечения автоматического синтеза пробного решения, для которого выполняется условие корректности.

Указанная цель достигается тем, что для получения пробных решений используется технология, базирующаяся на следующих соотношениях:

- решения Δq^k, k<n принадлежат множеству которое представляет собой множество n - мерных векторов Δq^k, таких, что для заданной погрешности ИТНП δh_зад и заданных ошибок в векторе поправок δΔq_зад, выполняется условие

а значение нормированной невязки

на множестве , достигает заданного минимума.

- пробные решения Δq^k, k<n вычисляются следующим образом:

Расчеты начинаются с Δq^k=0, p⁰=r⁰=A^TWΔh, k=1, 2, …, t.

Для определения множества корректности используются соотношения (5-9), в которых вектор Δh заменяется на вектор ошибок ИТНП δh. Технология формирования вектора δh в предлагаемом способе состоит в следующем: по результатам решения задачи повышения достоверности выборки ИТНП (1) формируется вектор δh:

где δh^j - вектор ошибок j-го сеанса ИТНП,

,

,

σ^j - среднеквадратическое отклонение ошибки измерений j-го сеанса ИТНП. σ^j вычисляется на очередном приближении (1) в процедуре повышения достоверности выборки ИТНП.

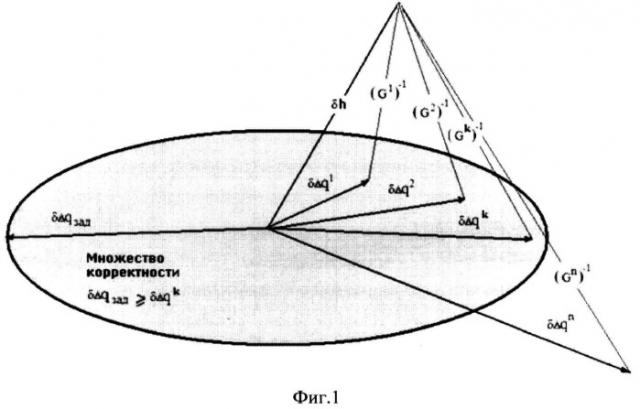
Формируется проверочная последовательность пробных решений. Для каждого к производится вычисление проекции ошибки вектора ИТНП на пространство уточняемых параметров. Геометрическая интерпретация указанной процедуры в предлагаемом способе приводится на фиг.1.

Для каждого индекса k, k=1, 2, 3, …, n, проверяется условие (3). Формируется набор индексов к, для которых выполнено (3), позволяющий сформировать множество и производится отбор пробных решений Δq^k, ассоциированных с δΔq^k и принадлежащих

Из множества пробных решений, принадлежащих в качестве оптимального выбирается вектор, для которого невязка незначимо отличается от минимальной среди всех невязок, соответствующих пробным решениям, а норма вектора решения при этом является минимальной. Выполнение этого требования является необходимым в связи с тем, что для получения вектора поправок используется технология линеаризации в окрестности начального приближения (3). Отбор невязок незначимо отличающихся от минимальной среди всех невязок, соответствующих пробным решениям, исходя из гипотезы о нормальном законе распределения погрешностей ИТНП и принимая величину (4) в качестве оценки среднеквадратического отклонения невязки, осуществляется с использованием критерия Фишера для проверки гипотезы , k=n, …, 1, где - значение минимальной невязки для векторов пробных решений. Условием принятия гипотезы Н₀ для уровня значимости α является выполнение неравенства (4)

в противном случае гипотеза Н₀ отвергается. При этом использованное в описании понятие «на коротком мерном интервале» имеет однозначное смысловое содержание для конкретного ИСЗ и является общепринятым в теории и практике траекторных радиотехнических измерений [3].

Источники информации

1. Бажинов И.К., Ястребов В.Д. Навигация в совместном полете космических кораблей «Союз» и «Аполлон». - М.: Мир, 1978. - 224 с.

2. Брандин В.Н., Васильев А.А., Куницкий А.А. Экспериментальная баллистика космических аппаратов. - М.: Машиностроение, 1984. - 264 с.

3. Траекторные радиотехнические измерения / Коллектив авторов под. ред. Агаджанова П.А. - М.: Сов. радио, 1969, 504.

Способ определения параметров движения искусственного спутника Земли по измерениям текущих навигационных параметров (ИТНП), заключающийся в том, что используют результаты радиоконтроля орбиты для определения параметров движения ИСЗ, отличающийся тем, что на коротком мерном интервале в автоматизированных системах навигационно-баллистического обеспечения (НБО) в условиях неполной реализации штатной схемы проведения радиоконтроля орбиты (РКО) используют технологию автоматического получения вектора поправок к уточняемым параметрам на основе выбора пробного решения, для которого выполняется условие корректности, определяемое введением множества векторов поправок (пробных решений) к уточняемым параметрам движения ИСЗ таких, что для заданной погрешности в ИТНП и для заданных ошибок в векторе поправок к уточняемым параметрам выполняется условие, при котором имеющимся погрешностям в ИТНП соответствуют ошибки в векторе поправок, не превосходящие заданные, а также для выбираемого пробного решения значение нормированной невязки незначимо отличается от минимальной по критерию Фишера, а норма вектора решения при этом является минимальной, обеспечивая требования эксплуатационно-технической документации ИСЗ.