Способ оценки жесткости и прочности автодорожных и железнодорожных мостов

Способ оценки жесткости и прочности автодорожных и железнодорожных мостов

Иллюстрации

Показать все

Реферат

Изобретение относится к области строительства и эксплуатации дорожных конструкций, а именно к оценке жесткости и прочности мостовых сооружений как автодорожных, так и железнодорожных.

Известен способ оценки состояния дорожных конструкций [патент РФ №2279653, МПК G01M 7/00, от 2006 г. (аналог)] [1].

В качестве эталонного сигнала данный способ предполагает единичный импульс, вызывающий собственные колебания дорожного покрытия и подстилающих слоев. Единичный импульс это воздействие сигнала вида

.

В качестве единичного импульса в аналоге предложено тарированное ударное воздействие в виде удара груза заданной массы сброшенной с заданной высоты.

Главным недостатком предложенного способа является то, что для искусственных сооружений этот способ не подходит, поскольку удар малой массы в первую очередь вызовет вязкие деформации дорожного покрытия моста и лишь частично будет передан на силовые элементы сооружения. Такой удар вызовет лишь незначительные колебания конструкции, которые будет трудно идентифицировать. Удар массивным грузом способен разрушить как дорожное покрытие, так и само сооружение.

Наиболее близким решением к предлагаемому является способ испытания железобетонного пролетного строения, основанный на применении одноканальной малогабаритной автоматизированной системы типа «Тензор-М», где в качестве эталонного сигнала выступает движение по мостовому сооружению груза (например, грузовика с песком или локомотива) с заданной массой и заданной скоростью. Движение груза вызывают колебания мостового сооружения, измеряемые датчиком вибрации [Бокарев С.А., Прибытков С.С., Яшнов А.Н. Содержание искусственных сооружений с использованием информационных технологий: Учебное пособие для вузов ж.-д. транспорта. - М.: ГОУ: Учебно-методический центр по образованию на железнодорожном транспорте», 2008. - 195 с. (прототип) [2].

При этом способе производят следующие операции:

- фиксируют изменения амплитуд колебаний с помощью индуктивных датчиков, установленных в середине пролета моста;

- фиксируют изменения напряжений в растянутой рабочей арматуре с помощью датчиков измерения деформаций, установленных в середине пролета в зоне расположения рабочей арматуры балки;

- измеряют раскрытие трещин с помощью датчиков измерения линейных перемещений, установленных над трещиной в подферменнике;

- все датчики предварительно калибруют;

- проводят фиксацию и первичный экспресс-анализ результатов в реальном масштабе времени;

- проводят камеральную обработку результатов с выявлением форм и частот свободных колебаний, динамических коэффициентов и логарифмических декрементов затухания, причем расчеты выполняют на персональных компьютерах с использованием специальных программ.

Данный способ обладает следующими недостатками.

1. Для того чтобы движение груза вызвало собственные колебания конструкции, длительность воздействия груза на пролет должна быть примерно равна периоду собственных колебаний конструкции.

2. Во время испытаний необходимо перекрыть движение транспорта для того, чтобы пропустить для измерений единичное транспортное средство с заданными массой и скоростью движения.

На примере Иркутского Академического моста это выглядит следующим образом. Моделированием с помощью конечноэлементного программного обеспечения «MIDAS/Civil» было получено, что период колебаний первой формы моста равен примерно 1 с при схеме пролетов 84+4×105+84 м.

Следовательно, для вызова собственных колебаний мостового сооружения тарирующий груз (грузовик) должен двигаться со скоростью примерно 360 км/ч. На практике эта скорость недостижима. Поэтому движение грузовика по автодорожному мосту или локомотива по железнодорожному вызовет вынужденные колебания системы, являющиеся суммой вынужденных колебаний от воздействия груза и собственных колебаний системы. При таком тарировочном воздействии оценка частоты собственных колебаний инженерного сооружения будет содержать трудно предсказуемую методическую погрешность.

3. Переходной процесс мостового сооружения не превышает 5 с. При разложении сигнала такой длительности в ряд Фурье шаг построения гармоник

Следовательно, предельно достижимая точность измерения частоты собственных колебаний мостового сооружения при таком способе измерения не может быть меньше 0,2 Гц, что недостаточно для оценки жесткости.

Таким образом, из-за низкой точности измерения и наличия методической погрешности данный способ непригоден для оценки жесткости и прочности мостового сооружения по частоте собственных колебаний.

Кроме перечисленных выше, в настоящее время для оценки прочности мостового сооружения на него устанавливают груз определенной массы, например, грузовики с песком, и делают необходимые измерения прогибов и напряжений в конструкциях с последующим сравнением полученных результатов с расчетными [СНиП 3.06.07-86. Мосты и трубы. Правила обследований и испытаний / Госстрой СССР. М.: ЦИТП Госстроя СССР, 1987. - 40 с.] [3]. Данный способ оценки жесткости и прочности сооружения используется при вводе моста в эксплуатацию и по ряду причин практического характера сложен для мониторинга за состоянием мостовых сооружений.

Поэтому разработка новых способов мониторинга жесткости и прочности мостовых сооружений имеет большое практическое значение.

Из теории колебаний известно, что, зная во времени закон движения масс деформируемой системы, например, автодорожного или железнодорожного моста, можно дать оценку жесткости и прочности системы. В самом общем виде частота свободных колебаний пролета моста около положения, в котором действие сил на него уравнивается можно записать в виде выражения [Клаф Р., Пеизиен Дж. Динамика сооружений: Пер. с аигл. - М.: Стройиздат, 1979. - 320 с.] [4]

,

где m - масса пролета моста; с - коэффициент характеризующий жесткость сооружения.

Если исходить из предположения о том, что при последующих измерениях ω₁ масса пролета моста, складывающаяся из массы самого сооружения и массы, расположенных на нем транспортных средств, изменяется незначительно, то по изменению ω₁ можно судить об изменении жесткости и, следовательно, прочности сооружения.

Для практического измерения ω₁ на мостовое сооружение необходимо подать тестовый сигнал, раскачивающий сооружение.

Возможны следующие варианты тестовых сигналов:

1. Тестовый сигнал с частотой вынужденных колебаний ω, равных частоте свободных колебаний пролета моста ω₁.

2. Тестовый сигнал в виде единичной ступенчатой функции l(t). На практике этот способ можно реализовать путем сброса массивного груза на мостовой пролет.

3. Тестовый сигнал в виде единичной импульсной функции g(t). На практике этот способ реализуют передвижением по мостовому сооружению единичного транспортного средства.

4. Тестовый сигнал с постоянным спектром S(ω)=const, т.е. белый шум.

В первом случае на сооружение устанавливается вибратор, например, электродвигатель с эксцентрично расположенным грузом на валу, раскачивающий сооружение с заданной частотой вынужденных колебаний ω.

Недостатком данного способа оценки жесткости и прочности сооружения является то, что в этом случае точность измерения ω₁ определяется точностью выдерживания оборотов электродвигателя. В свою очередь выдерживание оборотов электродвигателя с высокой заданной точностью является достаточно сложной инженерной задачей. Поэтому точность измерения частоты собственных колебаний моста при таком способе измерения невысока. Практика показывает, что усталостные разрушения, например трещины конструкции, незначительно изменяют величину ω₁, поэтому в силу больших погрешностей измерения частоты свободных колебаний пролета моста данный способ не позволяет оценить изменение прочности сооружения.

Второй способ, когда тестовым сигналом является однократное силовое воздействие на пролет моста, также не дает требуемой точности. Выше это было показано на примере [1].

Третий способ также не дает требуемой точности, что было показано на примере [2].

Наиболее перспективным способом измерения частоты свободных колебаний пролета моста около положения, в котором действие сил на него уравнивается, является применение тестового сигнала белый шум. При этом в качестве эталонного сигнала близкого к белому шуму предлагается использовать поток транспортных средств или движение железнодорожного эшелона через мост.

Техническим результатом предлагаемого способа является повышение точности и достоверности мониторинга жесткости и прочности конструкции.

Технический результат достигается тем, что предлагается применить наиболее перспективный способ измерения частоты свободных колебаний пролета моста около положения, в котором действие сил на него уравнивается, является применение тестового сигнала вида белый шум. В этом случае величина ω₁ может быть измерена с любой наперед заданной точностью как максимум спектра сигнала от реакции мостового сооружения на белый шум. При этом в качестве эталонного сигнала близкого к белому шуму предлагается использовать поток транспортных средств или движение железнодорожного эшелона через мост.

Далее применение предлагаемого способа оценки жесткости и прочности автодорожных и железнодорожных мостов будем рассматривать на примере Иркутского Академического моста через реку Ангару (фиг.1).

Мост через Ангару длиной 1.6 км выполнен из неразрезных предварительно напряженных железобетонных пролетных строений. Русловая часть моста представлена пролетным строением по схеме 84+4×105+84.

В настоящее время для наблюдения за состоянием руслового пролетного строения Академического моста используется системы автоматизированного и неавтоматизированного деформационного мониторинга [Быкова Н.М., Баранов Т.М. Технологии управления геодинамической безопасностью и долговечностью городских мостов /Превентивные меры по уменьшению природных и техногенных бедствий/ Тр. IV Международного геотехнического симпозиума: Хабаровск, 2011.] [5].

В системе автоматизированного деформационного мониторинга используется трехосный форсбалансный сервоакселерометр MS2004+, изготовленный фирмой Syscom Instruments SA (www.syscom.ch). Датчик позволяет измерять сигнал вибрации в диапазоне от 0 до 150 Гц при изменении температуры от -40 до +85°C.

В системе неавтоматизированного деформационного мониторинга показания переносного вибродатчика снимаются на карманный компьютер по каналу Bluetooth с помощью программного обеспечения системы Тензор.

Система автоматизированного деформационного мониторинга работает в штатном режиме с начала апреля 2010 года [Быкова Н.М., Зайнабдинов Д.А., Баранов Т.М., Мишутин В.О. Система автоматизированного мониторинга геодинамической безопасности городских мостов/Транспортное строительство №7, М.: 2011] [6].

Система неавтоматизированного деформационного мониторинга работает с 2008 года.

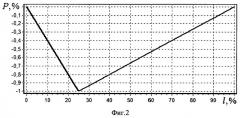
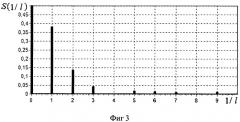
Для пояснения физики процесса представим простейшую качественную модель мостового сооружения в виде балки, длинною l, лежащей на двух опорах. В произвольном месте балки расположим точечную нагрузку - автомобиль единичного веса. Данная нагрузка создаст распределение сил треугольной формы. Модель распределения нагрузки на балку от единицы автотранспорта, расположенной на 25% от начала пролета представлена на фиг.2. Ее можно разложить на ряд пространственных гармоник, модуль амплитуды которых показан на фиг.3.

Как видно половина веса единицы автотранспорта приходится на постоянную составляющую, равномерно распределенную по всей длине пролета моста. Первая гармоника пространственной частоты обратно пропорциональна длине пролета моста 1/l. Вторая гармоника, соответственно 2/l, третья 3/l и т.д. Если автомобиль движется по мосту, то по мере перемещения его веса амплитуды пространственных гармоник начнут изменяться во времени, создавая колебания балки во времени со сложной спектральной характеристикой.

Ряд Фурье количественной модели мостового сооружения будет отличаться от простейшей балочной модели более сложным пространственным спектром. В общем случае из-за сложной конструкции мостового сооружения в пространственном спектре между гармониками кратными длине пролета (1/l, 2/l, l/3 и т.д.) должны неминуемо появиться дольные гармоники, не укладывающиеся целое число раз в длину пролета l.

Для примерной оценки реакции во времени пролета мостового сооружения на движение транспортного потока достаточно рассмотреть только постоянную составляющую единичной нагрузки. Со средней скоростью 21 м/с автомобиль проходит по 84 м пролету моста за 4 с.

При равномерном потоке автотранспорта через мостовой пролет с интервалом в 4 с.ожидаемый спектр шумов от потока автомашин представлен на фиг.4.

Для данной длины пролета и заданной скорости движения пространственная постоянная составляющая дает бесконечный ряд гармоник. Гармонику с минимальной частотой ω₁ принято называть частоту собственных колебаний пролета моста по первой форме, удвоенной частоты второй форме и т.д.

Поскольку спектр на фиг.4 был построен только для постоянной составляющей простейшей модели, то реальный спектр должен содержать множество дополнительных гармоник от кратных и дольных пространственных гармоник нагрузки на мост.

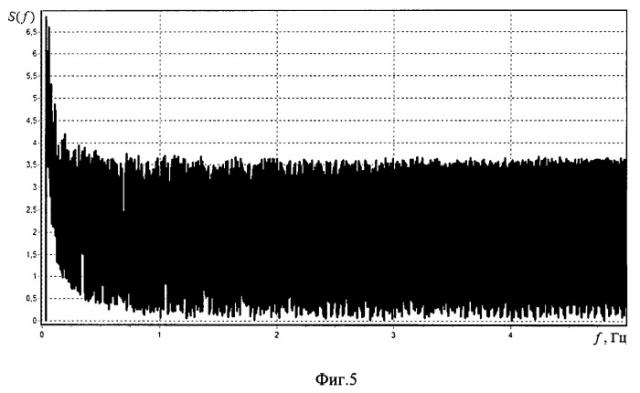
Реальный спектр реакции пролета среднего коммунального моста через р. Ангару на проезжающий автотранспорт показан на фиг.5. Спектр получен по сигналу тензодатчика, измеряемого с частотой 50 Гц. Как видно, характер спектра на фиг.5 хорошо согласуется с моделью на фиг.4. Кроме того, начиная с 1 Гц спектр на фиг.5 не изменяется. Это позволяет сделать практический вывод о том, что поток автотранспорта или железнодорожный эшелон, проходящий по мосту, можно рассматривать как тестовый сигнал вида белый шум.

Спектральную плотность PF(co) реакции моста на белый шум S(ω) можно представить выражением:

где Ф(ω) - амплитудно-частотная характеристика (АЧХ) пролета моста;

S(ω) - спектр сигнала белый шум.

Функция Ф(ω) обладает следующими основными свойствами:

Ф(0)=1; Ф(∞)=0.

Далее будем полагать, что максимум Ф(∞) приходится на резонансную частоту собственных колебаний пролета моста по первой форме ω₁.

В общем виде показания вибродатчика можно представить как:

.

где - ускорение середины пролета моста; C - постоянная составляющая измерений.

Если принять C=0, то после первого интегрирования сигнала (2) получим скорость перемещения центра конструкции:

.

После интегрирования (3) будет получена амплитуда перемещения середины пролета мостового сооружения:

.

Поскольку в дальнейшем предполагается разложение сигнала y(t) на гармоники, постольку интегрирование (3) и (4) можно заменить умножением на некий масштабный коэффициент. При этом используются следующие зависимости:

и .

Сигнал (4), полученный на интервале Т_оц раскладываются в ряды Фурье с шагом Ω_ш методом Дискретного Преобразования Фурье (ДПФ) для построения АЧХ. Число шагов определяется необходимой точностью измерений ω₁. Минимальная частота гармоники исходного сигнала, амплитуду которой можно найти методом ДПФ зависит от Т_оц:

.

Максимальная частота согласно теореме Котельникова равна половине частоты дискретизации. В рассматриваемом случае это 50 Гц.

При ДПФ, амплитуда каждой гармоники ω_i-=Ω_min+Ω_шi, составляющей АЧХ, определяется алгоритмом:

.

где - канал синусного опорного сигнала;

- канал косинусного опорного сигнала;

;

;

T - период дискретизации сигнала y(k);

- число точек, составляющих целое число периодов ω_i, помещающихся в N отсчетах входного сигнала;

- вещественное число отсчетов, приходящихся на период гармоники ω_i;

Int - функция, выделяющая целую часть вещественного числа.

Результатом построения спектральной функции W(ω_i) по выражению (5) является график, показанный на фиг.6.

Для построения Ф(ω) по W(ω) спектральную функцию на фиг.6 необходимо очистить. Для этого предлагается использовать КИХ фильтр Фурье. Разностное уравнение КИХ-фильтра Фурье размерности N_ф имеет вид:

y(nT)=h(1)x(nT)+h(2)x[(n-1)T]+h(3)x[(n-2)T]+…+n(N_ф)x[(n-N_ф+1)T],

где ;

, ;

- коэффициенты КИХ-фильтра Фурье;

К=1 - коэффициент усиления фильтра;

ωс=2πF_c - полоса пропускания фильтра.

Опытным путем было установлено, что наилучшие результаты по очистке спектральной функции дает КИХ-фильтр Фурье с параметрами N_ф=301 и F_c=1,1. Амплитудно-частотная характеристика фильтра показана на фиг.7. На фиг.7 значение f обозначает условную частоту АЧХ фильтра.

На основании (1), (4), (5) и алгоритма КИХ-фильтра Фурье было разработано программное обеспечение для построения Ф(ω) и оценки ω₁.

При первом построении Ф(ω) программа автоматически выявляет экстремумы и сохраняет их частоты в файле. При повторном и последующих построениях Ф(ω) частоты выявленных экстремумов сравниваются частотами с сохраненными в файле. Частоты, отличающиеся менее чем на 1%, помечаются флажком на нижней части графика (фиг.8).

Первый экстремум ω₁=2.518 Гц равен частоте собственных колебаний пролета моста по первому тону. Эта частота и является предметом мониторинга. Экстремумы на частотах 20 и более Герц являются резонансными частотами собственных колебаний вибродатчика.

При использовании вибродатчика MS2004+ для оценки жесткости и прочности пролета мостового необходима запись его показаний на карманный компьютер с последующей перезаписью по каналу USB на персональный компьютер, используемый для накопления результатов мониторинга. Практика показывает, что для обеспечения заданной точности измерения ω_i период измерения вибраций пролета Т_оц должен составлять примерно 3-4 мин.

Как было показано выше, в настоящее время предельно достижимая точность измерения ω₁, полученная методом [2] не может превышать 0,2 Гц.

Достигнутая в настоящее время точность измерения ω₁ предлагаемым методом составляет 0,003 Гц. При необходимости эту точность можно увеличить путем изменения Т_оц.

Источники информации

1. Патент РФ №2279653, МПК G01M 7/00, от 2006 г.

2. Бокарев С.А., Прибытков С.С., Яшнов А.Н. Содержание искусственных сооружений с использованием информационных технологий: Учебное пособие для вузов ж.-д. транспорта. - М.: ГОУ: Учебно-методический центр по образованию на железнодорожном транспорте», 2008. - 195 с.

3. СНиП 3.06.07-86. Мосты и трубы. Правила обследований и испытаний / Госстрой СССР. М.: ЦИТП Госстроя СССР, 1987. - 40 с.

4. Клаф Р., Пеизиен Дж. Динамика сооружений: Пер. с англ. - М.: Стройиздат, 1979. - 320 с.

5. Быкова Н.М., Баранов Т.М. Технологии управления геодинамической безопасностью и долговечностью городских мостов / Превентивные меры по уменьшению природных и техногенных бедствий / Тр. IV Международного геотехнического симпозиума: Хабаровск, 2011.

6. Быкова Н.М., Зайнабдинов Д.А., Баранов Т.М., Мишутин В.О. Система автоматизированного мониторинга геодинамической безопасности городских мостов / Транспортное строительство, №7, М.: 2011.

Способ оценки жесткости и прочности автодорожных и железнодорожных мостов, заключающийся в том, что предлагается применить способ измерения, основанный на применении тестового сигнала вида белый шум, при котором частота собственных колебаний пролета моста около положения, в котором действие сил на него уравнивается, может быть измерена с любой наперед заданной точностью как максимум спектра сигнала от реакции мостового сооружения на белый шум, а в качестве эталонного сигнала, близкого к белому шуму, предлагается использовать поток транспортных средств или движение железнодорожного эшелона через мост.