Способ определения наличия гармонических составляющих и их частот в дискретных сигналах

Способ определения наличия гармонических составляющих и их частот в дискретных сигналах

Иллюстрации

Показать все

Реферат

Изобретение относится к области цифровой обработки сигналов и может быть использовано для определения наличия гармонических составляющих и их частот в сигналах различного происхождения при решении задач неразрушающего контроля и диагностики оборудования на основе корреляционного анализа.

Известен способ определения наличия гармонической составляющей и ее периода в дискретном сигнале f(t_i) с помощью автокорреляционной функции, выбранный в качестве прототипа [Эммануил С. Айфичер, Барри У. Джервис. Цифровая обработка сигналов: практический подход. 2-е изд. - М.: Вильяме, 2008. - 992 с.]. Сущность способа заключается в прямом преобразования Фурье анализируемого дискретного сигнала в форме быстрого преобразования Фурье размерностью 2ⁿ, определении комплексно-сопряженных значений результатов прямого преобразования Фурье анализируемого дискретного сигнала, попарного умножения полученных комплексных сигналов прямого преобразования Фурье анализируемого дискретного сигнала с комплексно-сопряженными значениями прямого преобразования Фурье анализируемого дискретного сигнала. Полученные значения подвергают обратному преобразованию Фурье для определения периода колебаний гармонической составляющей по автокорреляционной функции и рассчитывают частоту.

Недостатком такого решения является то, что полученная в результате расчетов автокорреляционная функция не позволяет определить наличие гармонических составляющих и их частот в дискретном сигнале, представленном суммой гармонических составляющих.

Задачей изобретения является определение наличия гармонических составляющих и их частот в дискетном сигнале по автокорреляционной функции.

Это достигается тем, что в способе определения наличия гармонических составляющих и их частот в дискретных сигналах, также как в прототипе, производят прямое преобразование Фурье анализируемого дискретного сигнала в форме быстрого преобразования Фурье размерностью 2ⁿ, определяют комплексно-сопряженные значения результатов прямого преобразования Фурье анализируемого дискретного сигнала, попарно умножают полученные комплексные сигналы прямого преобразования Фурье анализируемого дискретного сигнала с комплексно-сопряженными значениями прямого преобразования Фурье анализируемого дискретного сигнала, и производят обратное преобразование Фурье.

Согласно изобретению из полученного произведения P_j выбирают значения и формируют m сигналов M^k,

где j=0,1, …, 2^n-1+1;

m=2, 3, …, 2^n-1+1;

k=0, 1, …, m-1,

согласно выражению

Полученные сигналы M^k подвергают обратному преобразованию Фурье Z^k=F^-1[M^k].

По результатам обратного преобразования Фурье определяют частотно-временную автокорреляционную функцию

где t_i∈[t_min, t_max];

f_k∈[f_min, f_max];

;

;

;

;

;

f_d - частота дискретизации сигнала.

По полученным результатам строят график частотно-временной автокорреляционной функции R(f, t), по которому судят о наличии в анализируемом дискретном сигнале гармонических составляющих и их частотах.

Заявленный способ определения наличия гармонических составляющих и их частот в дискретных сигналах позволяет определить наличие гармонических составляющих и их частоты за счет выбора из произведения P_j и формирования m сигналов M^k согласно приведенному выражению (1), что позволяет рассчитать частотно-временную автокорреляционную функцию по m частотам, при этом обеспечено высокое быстродействие и универсальность реализации способа.

На фиг.1 приведена аппаратная схема устройства, реализующего рассматриваемый способ определения наличия гармонических составляющих и их частот в дискретных сигналах.

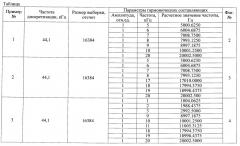
В таблице приведены исходные данные и результаты анализа тестовых примеров при m=1121.

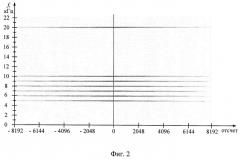
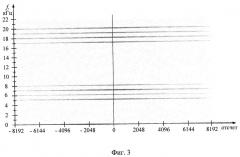
На фиг.2-4 приведены графики частотно-временной автокорреляционной функции результатов анализа тестовых примеров.

Заявленный способ определения наличия гармонических составляющих и их частот в дискретных сигналах может быть осуществлен с помощью схемы (фиг.1), содержащей датчик для получения анализируемого сигнала 1 (ДАС), подключенный к блоку аналого-цифрового преобразования 2 (АЦП), выход которого соединен с входом блока прямого преобразования Фурье 3 (БФ), выход которого подсоединен к входу блока определения комплексно-сопряженного значения 4 (БОК). Выход блока прямого преобразования Фурье 3 (БФ) и блока определения комплексно-сопряженного значения 4 (БОК) соединены с входом блока умножения 5 (БУ), к которому последовательно подключены блок формирования сигналов 6 (БФС), блок обратного преобразования Фурье 7 (БОФ) и блок интерпретации 8 (БИ).

В качестве датчика анализируемого сигнала 1 (ДАС) могут быть использованы датчики тока, например, промышленный прибор КЭИ-0.1 или датчик напряжения - трансформатор напряжения (220/5 В). Блок аналого-цифрового преобразования 2 (АЦП) может быть реализован на основе аналого-цифрового преобразователя ADS7827. Блок прямого преобразования Фурье 3 (БФ), блок определения комплексно-сопряженного значения 4 (БОК), блок умножения 5 (БУ), блок формирования сигналов 6 (БФС), блок обратного преобразования Фурье 7 (БОФ), блок интерпретации 8 (БИ) могут быть выполнены на микроконтроллере серии AVR32 производителя Atmel АТ32АР7000.

С выхода датчика 1 (ДАС) анализируемый сигнал, например, y(t)=u(t)=1·sin(2·π·5000·t)+1·sin(2·π·6000·t)+1·sin(2·π·7000·t)+

+1·sin(2·π·8000·t)+1·sin(2·π·9000·t)+1·sin(2·π·10000·t)+1·sin(2·π·20000·t),

где u(t) - многочастотный сигнал напряжения (таблица, пример №1), поступает на вход аналого-цифрового преобразователя 2 (АЦП), с выхода которого дискретизированный сигнал y(t_i)=u(t_i)=1·sin(2·π·5000·t_i)+1·sin(2·π·6000·t_i)+1·sin(2·π·7000·t_i)+

+1·sin(2·π·8000·t_i)+1·sin(2·π·9000·t_i)+1·sin(2·π·10000·t_i)+

+1·sin(2·π·20000·t_i),

где t_i=Δt·i,

где i=1,2,…,n;

N=2ⁿ=2¹⁴=16384 - размер выборки для быстрого преобразования Фурье;

- шаг дискретизации сигнала u(t_i),

поступает на вход блока прямого преобразования Фурье 3 (БФ), где выполняют прямое преобразование Фурье входного сигнала. С выхода блока прямого преобразования Фурье 3 (БФ) результаты прямого преобразования Фурье в виде комплексного сигнала размерностью 2ⁿ⁼¹+1=8193 поступают на вход блока определения комплексно-сопряженного значения 4 (БОК), где определяют комплексно-сопряженные значения для каждого элемента сигнала. Результаты прямого преобразования Фурье БПФ 3 (БФ) и блока определения комплексно-сопряженного значения 4 (БОК) поступают на вход блока умножения 5 (БУ), где выполняют попарное умножение двух комплексных сигналов. С выхода блока умножения 5 (БУ) результаты умножения в виде комплексного сигнала размерностью 2^n-1+1=8193 поступают на вход блока формирования сигналов 6 (БФС), где формируют m=1121 комплексных сигналов размерностью 2^n-1+1=8193 согласно выражению (1). С выхода блока формирования сигналов 6 (БФС) полученные комплексные сигналы поступают на вход блока вычисления обратного преобразования Фурье 7 (БОФ), где выполняют обратное преобразование Фурье над каждым комплексным сигналом. С выхода блока вычисления обратного преобразования Фурье 7 (БОФ) результаты обратного преобразования Фурье в виде действительных m=1121 сигналов размерностью N=2ⁿ=2¹⁴=16384 поступают на вход блока интерпретации 8 (БИ), где согласно выражению (2) определяют частотно-временную автокорреляционную функцию.

Для m=1121 и k=254 получили f_k=f₂₅₄=5000.6250 Гц,

при k=305 f_k=f₃₀₅=6004.6875 Гц,

при k=356 f_k=f₃₅₆=7008.7500 Гц,

при k=406 f_k=f₄₀₆=7993.1250 Гц,

при k=457 f_k=f₄₅₇=8997.1875 Гц,

при k=508 f_k=f₅₀₈=10001.2500 Гц,

при k=1016 f_k=f₁₀₁₆=20002.5000 Гц.

Полученные частотно-временные автокорреляционные функции (фиг.2) ярко выражены на семи частотах близких к частотам заданным в тестовом примере №1, что свидетельствует о наличии в анализируемом сигнале семи гармонических составляющих. Результат вычисления тестового примера в виде графика частотно-временной автокорреляционной функции представлен на фиг.2. Расчетные значения частотно-временной автокорреляционной функции R(f, t) представлены цветом: максимальное значение отображено черным цветом, минимальное - белым, а промежуточные значения - в уровнях серого цвета. На фиг.3 приведены частотно-временные автокорреляционные функции результата анализа тестового примера №2, по которым видно, что полученные частотно-временные автокорреляционные функции (фиг.3) ярко выражены на восьми частотах близких к частотам заданным в тестовом примере, что свидетельствует о наличии в анализируемом сигнале восьми гармонических составляющих. На фиг.4 приведены частотно-временные автокорреляционные функции результата анализа тестового примера №3, по которым видно, что полученные частотно-временные автокорреляционные функции (фиг.3) ярко выражены на девяти частотах близких к частотам заданным в тестовом примере, что свидетельствует о наличии в анализируемом сигнале девяти гармонических составляющих.

Способ определения наличия гармонических составляющих и их частот в дискретных сигналах, включающий прямое преобразование Фурье анализируемого дискретного сигнала в форме быстрого преобразования Фурье размерностью 2ⁿ, определение комплексно-сопряженных значений результатов прямого преобразования Фурье анализируемого дискретного сигнала, попарное умножение полученных комплексных сигналов прямого преобразования Фурье анализируемого дискретного сигнала с комплексно-сопряженными значениями прямого преобразования Фурье анализируемого дискретного сигнала, обратное преобразование Фурье, отличающийся тем, что из полученного произведения P_j попарного умножения комплексных сигналов прямого преобразования Фурье анализируемого дискретного сигнала с комплексно-сопряженными значениями прямого преобразования Фурье анализируемого дискретного сигнала выбирают значения и формируют m сигналов M^k,где j=0, 1,…, 2^n-1+1;m=2, 3,…, 2^n-1+1;k=0, 1,…, m-1,согласно выражению полученные сигналы M^k подвергают обратному преобразованию Фурье Z^k=F^-1[M^k], определяют частотно-временную автокорреляционную функцию ;где t_i∈[t_min,t_max];f_k∈[f_min,f_max]; f_d - частота дискретизации сигнала,далее по полученным результатам строят график частотно-временной автокорреляционной функции R(f,t), по которому судят о наличии в анализируемом дискретном сигнале гармонических составляющих и их частотах.