Способ перехвата воздушных целей летательными аппаратами

Способ перехвата воздушных целей летательными аппаратами

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к способам наведения летательных аппаратов (ЛА) на воздушные цели, в частности, к способам наведения летательных аппаратов, используемым в системах командного радиоуправления.

В современных условиях большое внимание уделяется системам управления многофункциональными самолетами. При наведении на воздушные цели вначале выполняется этап дальнего наведения (ДН) [1, стр. 218, 219].

Значительную роль на этапе ДН играет процесс управления самолетами по курсу. Способы наведения по курсу предопределяют формирование требуемых значений ψ_T курса, обусловливающих желаемую траекторию наведения в горизонтальной плоскости. При этом параметры рассогласования, определяющие алгоритмы траекторного управления самолетом в режиме ручного управления, формируются по правилу:

в котором ψ_c - текущее значение курса.

Способы наведения самолетов, реализуемые системой дальнего наведения (СДН), должны обеспечивать: минимум времени наведения, максимальную дальность действия, минимальные мгновенные перегрузки ЛА, минимальный расход энергии управляющих сигналов, практическую реализуемость, инвариантность системы управления к условиям применения, сопряжение со способами, используемыми на последующих этапах выполнения боевой задачи. При этом наибольшее значение имеет хорошее сопряжение способов наведения СДН и используемой в дальнейшем системы самонаведения, при которой обеспечивается органичный (без существенных переходных процессов) переход авиационной системы радиоуправления от этапа дальнего к этапу ближнего наведения.

Среди известных способов наведения по курсу в СДН самолетами наибольшее применение находят метод маневра, метод перехвата и прямой метод [1, стр. 228-231].

При прямом методе, называемом также методом погони, требуется все время совмещать продольную ось самолета с направлением на цель. К недостаткам метода относятся: сложность пилотирования самолетом в связи с постоянным изменением курса и крена, увеличенное время полета до встречи.

Метод маневра обеспечивает вывод самолета в зону обнаружения цели бортовой РЛС, оптико-электронной станцией или оптическим прицелом под заданным углом ψ_к на заданном расстоянии до цели. Недостатками метода являются: большое время, затрачиваемое на выход самолета на рубеж захвата, большой расход топлива, что сокращает время на ведение воздушного боя, ограничения на ракурсы перехвата из передней полусферы, обусловленные необходимостью вывода самолета в заднюю полусферу, сложность расчетов траектории и ее выполнения.

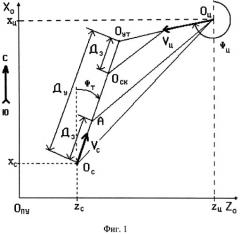
Способ перехвата, который взят в качестве прототипа, представляет собой разновидность способа параллельного сближения [1, стр. 230-231]. Его особенностью является то, что по методу параллельного сближения наводится не сам самолет, а некоторая вспомогательная (фиктивная) точка A, расположенная по вектору скорости V_c на расстоянии Д_з от наводимого самолета (фиг. 1). В качестве дальности Д_з может использоваться дальность обнаружения бортовой РЛС. Это означает, что в процессе дальнего наведения прямая АО_ц перемещается параллельно самой себе. Такой прием обеспечивает нахождение самолета в точке О_ск на рубеже Д_з в тот момент, когда точка A «встретится» в упрежденной точке встречи О_ут с целью.

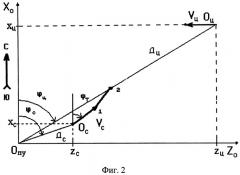
На чертеже точки О_с, О_пу и О_ц соответствуют положению самолета, пункта управления (наведения) и цели; V_c и V_ц - скорости наводимого самолета и цели; х_ц , z_ц и х_с, z_c - текущие прямоугольные координаты цели и самолета. Оценки координат х_ц , z_ц и х_с, z_c формируются на основании измеренных в РЛС, связанной с пунктом управления, дальностей Д_ц, Д_с и азимутов φ_ц, φ_с цели и самолета (фиг. 2) с использованием правил:

Используя координаты цели х_ц, z_ц и самолета х_с, z_c и учитывая, что упрежденная дальность Д_у равна сумме Д_з и расстояния О_сО_ск, пролетаемого самолетом за время наведения t_н (фиг. 1), получают систему уравнений [1, стр.230]: -

с тремя неизвестными ψ_Т, t_н и Д_у. При получении (3) полагалось, что цель и самолет движутся равномерно и прямолинейно со скоростями V_ц и V_c и курсовыми углами ψ_ц и ψ_Т соответственно. Решая эту систему при условии, что прямоугольные координаты определяются по правилам (1), (2), вычисляют ψ_Т, t_н и Д_у.

Из (3) следует, что для реализации способа перехвата необходимо оценивать прямоугольные координаты цели и самолета, скорости самолета и цели и курсовой угол цели ψ_ц. Последнее требует достаточно длительного сопровождения цели.

Достаточно просто решение системы (3) получается при условии, что самолет наводится на встречных либо догонных курсах. В такой ситуации с учетом (2) из (3) получают [1, стр. 231]:

где

Из (4) и (5) следует, что для реализации способа перехвата необходимо оценивать дальности и азимуты цели и самолета, а также скорости V_ц и V_c и курсовой угол цели ψ_ц.

Основными достоинствами способа перехвата являются:

высокая экономичность наведения, обусловленная наведением в упрежденную точку практически по прямолинейной траектории;

обеспечение заданного рубежа перехвата при любом ракурсе наведения.

Следует также отметить, что данный способ обеспечивает хорошее сопряжение прямолинейного участка траектории самолета с траекторией ракеты [2, стр. 388]. Недостатком известного способа перехвата является низкий уровень ситуационной осведомленности летчика наводимого самолета об ожидаемых результатах процесса наведения на заданную воздушную цель, что затрудняет оценку им тактической ситуации. Кроме того, для реализации способа-прототипа необходимо решение системы нелинейных уравнений (3), что требует выполнения сложной вычислительной процедуры, которая организуется в информационно-вычислительной системе пункта управления (ПУ). При линеаризации уравнений (3) требуемый курс самолета вычисляется с большими ошибками при ракурсах цели, отличных от нулевых.

Цель изобретения состоит в повышении ситуационной осведомленности летчика о возможных конечных результатах наведения и в упрощении вычислительной процедуры определения требуемого курса и времени наведения.

Технический результат заключается в повышении информативности системы дальнего наведения, основанное на введении процедур формирования данных, характеризующих пространственное положение точки перехвата и времени наведения на воздушную цель, и визуального отображения этих данных на наводимом самолете, в снижении вычислительных затрат в информационно-вычислительной системе ПУ. Кроме того, обеспечивается расширение области применения способа перехвата при наведении не только на воздушные цели, но и на другие виды целей, например, надводные цели.

Для реализации заявленного технического результата в горизонтальной плоскости измеряют полярные координаты цели и самолета, на пункте управления оценивают полярные и прямоугольные координаты цели и самолета, курс цели и скорости самолета и цели, задают вспомогательную точку A, расположенную на линии по вектору скорости V_c самолета на расстоянии Д_з, определяют требуемый курс ψ_T движения самолета, значение которого передают с ПУ на самолет, где измеряют его текущий курс ψ_с и определяют параметры управления Δψ_ψ=ψ_T-ψ_c, осуществляют управление траекторией движения самолета. В отличие от прототипа на ПУ оценивают курс ψ_ñ самолета и задают прямоугольные координаты фиктивной точки A

z_a=z_c+Д_зsinψ_T

х_а=x_c+Д_зcosψ_T

где х_а, z_a, х_с, z_c - оценки прямоугольных координат точки A и самолета, рассчитывают угол визирования цели относительно точки A, определяют углы пеленга φ_а и φ_ц, представляющие собой углы между векторами скоростей V_c и V_ц точки A и цели соответственно и линией визирования «точка A - цель», определяют значение требуемого курса ψ_T движения самолета из условия равенства проекций скоростей точки A и цели на перпендикуляр к линии визирования «точка A - цель», летчик оценивает ожидаемые результаты решения задачи перехвата самолетом воздушной цели с использованием визуального отображения на экране индикатора прогнозируемого положения цели (точки перехвата) в конце этапа дальнего наведения и времени наведения, для чего в вычислительной системе ПУ находят прямоугольные координаты точки перехвата по формулам:

x_yт=x_a+V_ct_нcosψ_T, z_ут=z_a+V_ct_нsinψ_T,

либо

x_yт=x_ц+V_цt_нcosψ_ц, z_ут=z_ц+V_цt_нsinψ_ц,

и время наведения

,

либо

,

где x_ц, z_ц - оценки прямоугольных координат цели, ψ_ц - курс цели, осуществляют вывод этих данных и передачу их через командную радиолинию управления на систему отображения на самолете.

Перечень фигур:

Фиг.1 и Фиг.2 Способ перехвата по прототипу [1, стр. 230-231].

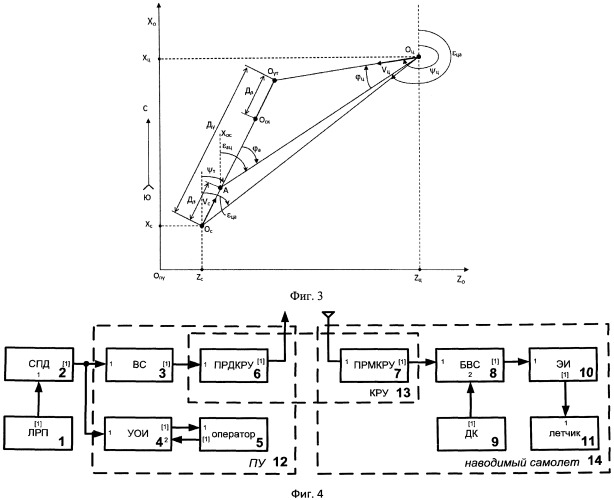
Фиг.3. Геометрия наведения самолета на воздушную цель при использовании предлагаемого способа.

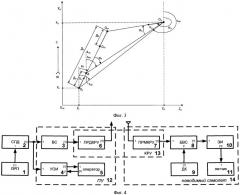
Фиг.4. Обобщенная структурная схема системы радиоуправления.

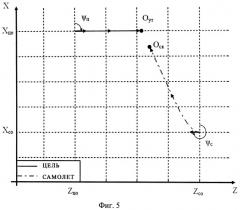
Фиг.5. Результаты моделирования перехвата для способа прототипа.

Фиг.6. Результаты моделирования перехвата для способа прототипа при линеаризованном алгоритме.

Фиг.7. Результаты моделирования перехвата для способа прототипа при линеаризованном алгоритме с новыми исходными данными для истребителя.

Фиг.8. Результаты моделирования перехвата для модифицированного способа.

Для получения технического результата предлагаемым способом воспользуемся известными уравнениями для метода параллельного сближения, при котором линия АО_ц, соединяющая точку A и цель О_ц, должна перемещаться параллельно самой себе.

Геометрия взаимного положения всех объектов, участвующих в процессе наведении самолета на воздушную цель, показана на фиг.3.

В треугольнике АО_утО_ц углы пеленга φ_а и φ_ц представляют собой углы между векторами скоростей V_c и V_ц соответственно и линией визирования АО_ц. Угол визирования ε_ц цели из точки A образован лучами АХ_ос и АО_ц. Соответственно ε_ца - угол визирования точки A относительно цели О_ц.

Из фиг.3 видно, что прямоугольные координаты точки A равны:

Углы визирования связаны с прямоугольными координатами соответствующих точек A, О_ц и О_с следующими соотношениями (фиг.3):

В свою очередь, углы пеленга φ_а и φ_ц определяются следующими равенствами:

Как известно, при методе параллельного сближения точки A и цели проекции скоростей точки A и цели, перпендикулярные к линии визирования АО_ц, должны быть равными друг другу:

При подстановке в (9) значений φ_а и φ_ц из (8) получаем:

В (10) ψ_Т - требуемый курс самолета при точной реализации модифицированного способа перехвата, когда курс ψ_с самолета совпадает с его требуемым значением. Отсюда следует, что требуемый курс самолета:

В процессе наведения фактический ψ_c и требуемый ψ_т курсы могут не совпадать. Поэтому при определении прямоугольных координат точки A в выражения (6-7) вместо ψ_T необходимо подставлять ψ_с. Отсюда следует, что модифицированный способ перехвата требует дополнительно оценивать на ПУ курс ψ_с самолета по результатам первичных измерений полярных координат самолета.

Если перехват воздушной цели осуществляется при малых углах φ_а и φ_ц, т.е. на встречных либо догонных курсах, то формула (11) упрощается:

где a=V_ц/V_c - коэффициент, характеризующий соотношение скоростей цели и самолета.

Для нахождения времени наведения t_н можно воспользоваться соотношениями, которые связывают прямоугольные координаты точки перехвата, координаты точки A, прямоугольные координаты цели, требуемый курс самолета, курс цели и время наведения (фиг. 3):

,

,

Приравняв одноименные координаты точки перехвата из (13) и (14), находят время наведения:

либо

Для вычисления времени наведения t_H можно воспользоваться формулой (15) либо (16).

Необходимые для реализации способа перехвата оценки координат и параметров движения цели и самолета формируют с помощью известных алгоритмов оценивания (фильтрации), приведенных в научно-технической литературе, например в [3, стр. 183-217].

Оценить прогнозируемые результаты решения задачи перехвата самолетом воздушной цели летчик может, если использовать визуальное отображение на экране индикатора пространственного положения расчетной точки перехвата и указать время наведения. Для этого необходимо выполнить расчеты по формулам (13) - (16) и осуществить процедуру вывода и отображения результатов расчетов.

Реализация предлагаемого способа наведения обеспечивается системой радиоуправления, пример которой в виде обобщенной структурной схеме представлен на фиг. 4.

Координаты цели и самолета измеряются на радиолокационном посту (РЛП) 1 и посредством системы передачи данных (СПД) 2 транслируются на ПУ 12, где поступают в вычислительную систему (ВС) 3 и в устройство отображения информации (УОИ) 4. На пункте управления оператор 5 отвечает за общую организацию процесса наведения самолета на выбранную цель. При реализации модифицированного способа наведения оператор осуществляет контроль за процессом наведения. Для обеспечения успешного перехвата цели летчику необходимо знать возможные последствия принимаемых на ПУ решений и требования, предъявляемые к пилотированию им самолета. Применительно к решению конкретной задачи перехвата он должен иметь представление о возможном пространственном положении точки перехвата в момент окончания этапа ДН и продолжительность этапа ДН. Для этого в вычислительной системе 3 выполняются расчеты ее прямоугольных координат и времени наведения согласно выражениям (13) - (16).

Кроме этого в ВС 3 осуществляется оценивание координат и параметров движения цели и самолета, а также определение требуемого курса самолета. С помощью командной радиолинии управления (КРУ) 13 значение требуемого курса, координаты точки перехвата и время наведения передаются в бортовую вычислительную систему (БВС) 8 наводимого самолета 14. Датчик курса (ДК) 9 измеряет текущий курс самолета и выдает его значение в БВС 8, где вырабатывается параметр управления, отображаемый на экране индикатора (ЭИ) 10. Летчик 11 по ЭИ 10 оценивает тактическую обстановку, определяет значение параметра управления и пилотирует самолет так, чтобы поддерживать параметр управления, равным нулю.

Для оценки эффективности предлагаемого способа было выполнено моделирование процесса перехвата цели наводимым самолетом с ПУ. Для этого была разработана имитационная модель процесса перехвата.

При моделировании полагалось, что воздушная цель движется равномерно и прямолинейно.

Для наводимого самолета производные его прямоугольных координат при известных значениях скорости V_c и курса ψ_с рассчитываются по формулам:

, .

В этом выражении ψ_с - курс самолета, связанный с его боковым ускорением соотношением [1, стр.176]:

.

В простейшем случае боковое ускорение определяется формулой [1, стр.190]:

,

где к₁ - коэффициент передачи САУ и самолета, как объекта управления.

Так как самолет наводится на цель заявленным способом, то ψ_Т определяется выражением (14). Параметр управления вырабатывается согласно правилу

Δ_ψ=ψ_Т-ψ_с,

где ψ_с - моделируемый курс самолета.

Координаты точки A рассчитывались на основе соотношений (6).

Модели формирования углов визирования и пеленгов для разработанного способа перехвата описываются соотношениями (7) и (8).

Модели оценивания координат и параметров движения цели и самолета характеризуют алгоритмы построения их траекторий в информационно-вычислительной системе ПУ, которые основаны на фильтрации результатов косвенных измерений прямоугольных координат цели и самолета соответственно.

Моделирование перехвата воздушной цели было проведено в среде Matlab 7.3.0 для трёх вариантов вычисления заданного курса истребителя:

1) решалась нелинейная система уравнений (3);

2) заданный курс истребителя и время наведения находились с помощью линеаризованных уравнений (4) и (5);

3) требуемый курс вычислялся с помощью разработанного метода, на основании уравнения (11), а время наведения - в соответствии с одним из равнозначных уравнений (15), (16).

Вычисление требуемого курса истребителя проводилось с дискретностью пять секунд. Через те же временные интервалы определялись текущие координаты воздушной цели и истребителя. Моделирование всех трёх вариантов проводилось при следующих исходных данных: заданной дальности Д_з=30 км, начальном курсе истребителя ψ_с=270° и начальном курсе цели ψ_ц=90° и угле визирования цели относительно истребителя ε_сц=-45°.

Начальный курс истребителя ψ_о задавался обратным курсу цели ψ_ц, поэтому истребитель для выхода на требуемый курс выполняет разворот на угол Δψ_и=ψ_Т-ψ_о.

Результаты моделирования всех описанных вариантов наведения представлены на фиг. 5-8, на которых показаны траектории наведения самолета (пунктирная линия) на движущуюся цель (сплошная линия).

Результаты первого варианта моделирования перехвата по способу (3) цели показаны на фиг. 5.

Результаты второго варианта моделирования перехвата цели при линеаризации алгоритма наведения (3) показаны на фиг. 6.

Результаты второго варианта моделирования перехвата цели с новыми исходными, удовлетворяющим условиям линеаризации, при котором получено (4), данными истребителя показаны на фиг. 7.

Результаты моделирования третьего варианта (модифицированный алгоритм) перехвата показаны на фиг. 8.

Как видно из фиг. 6, при наведении истребителя по курсу, вычисляемому в соответствии с уравнением (4), происходит срыв перехвата цели. Это вполне объяснимо, так как при выводе уравнения (4) из системы (3) делается допущение о том, что наведение осуществляется на догонных либо встречных курсах. В связи с этим были изменено начальное положение истребителя таким образом, чтобы оно обеспечивало наведение истребителя с курсом, близким к встречному относительно цели (см. фиг. 7)

Как видно из фиг. 8, при наведении истребителя по курсу, вычисляемому в соответствии с уравнением (11) траектории истребителя и цели идентичны их траекториям в первом варианте перехвата. Таким образам, наведение на воздушную цель в соответствии с предлагаемым методом обеспечивает движение истребителя в точном соответствии с системой уравнений (3) с возможностью получения требуемого курса путем несложных вычислений.

Детальное моделирование процесса перехвата воздушной цели согласно модифицированному методу при произвольных начальных данных показало, что наведение самолета осуществляется с высокой точностью и обладает хорошей устойчивостью.

Таким образом, модифицированный метод перехвата по сравнению с известным методом характеризуется повышенной информативностью и простотой вычисления требуемого курса наводимого самолета и времени наведения.

Литература

1. Авиационные системы радиоуправления: учебник для военных и гражданских ВУЗов и научно-исследовательских организаций. / В.И. Меркулов, B.C. Чернов, В.А. Гандурин, В.В. Дрогалин, А.Н. Савельев. Под ред. В.И. Меркулова. - М.: Изд. ВВИА им. проф. Н.Е. Жуковского, 2008. Стр. 176, 190, 218, 219, 228-231.

2. Справочник офицера Военно-воздушных сил и войск противовоздушной обороны / под ред. И.П. Азаренко. - Минск: командование ВВС и войск ПВО, 2009 г. Стр. 338.

3. Кузьмин С.З. Цифровая радиолокация. Введение в теорию. - Киев: Издательство КВЩ, 2000. Стр. 183-217.

Способ перехвата самолетом воздушной цели, заключающийся в том, что в горизонтальной плоскости измеряют полярные координаты цели и самолета, на пункте управления (ПУ) оценивают полярные и прямоугольные координаты цели и самолета, курс цели и скорости самолета и цели, задают фиктивную точку A, расположенную на линии, совпадающей с вектором скорости V_c самолета на расстоянии Д_з от самолета, определяют значение требуемого курса ψ_T движения самолета, значение которого передают с ПУ на самолет, где измеряют его текущий курс ψ_с и определяют параметр управления Δψ=ψ_T-ψ_c, осуществляют управление траекторией движения самолетом, отличающийся тем, что на ПУ оценивают курс ψ_с самолета, выбирают точку A путем задания прямоугольных координатz_a=z_c+Д_зsinψ_T,х_а=x_c+Д_зcosψ_T,где x_a, z_a, x_c, z_c - оценки прямоугольных координат точки A и самолета, рассчитывают угол визирования цели относительно точки A, определяют углы пеленга φ_а и φ_ц, представляющие собой углы между векторами скоростей V_c и V_ц точки A и цели соответственно и линией визирования «точка A - цель», определяют значение требуемого курса ψ_T движения самолета из условия равенства проекций скоростей точки A и цели на перпендикуляр к линии визирования «точка A - цель», летчик оценивает ожидаемые результаты решения задачи перехвата самолетом воздушной цели с использованием визуального отображения на экране индикатора прогнозируемого положения цели в конце этапа дальнего наведения, совпадающей с точкой перехвата, и времени наведения, для чего в вычислительной системе ПУ находят прямоугольные координаты точки перехвата по формулам:x_yт=x_a+V_ct_нcosψ_T, z_ут=z_a+V_ct_нsinψ_T либоx_yт=x_ц+V_цt_нcosψ_ц, z_ут=z_ц+V_цt_нsinψ_ц и определяют время наведения где x_ц, z_ц - оценки прямоугольных координат цели, ψ_ц - курс цели, осуществляют вывод этих данных и передают их через командную радиолинию управления в систему отображения на самолете.