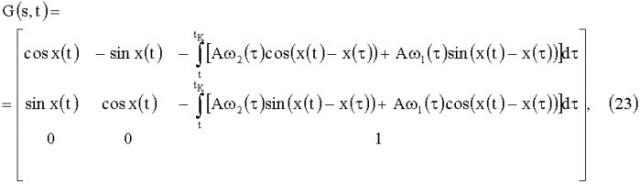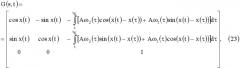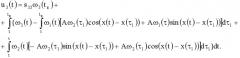Адаптивная система терминального управления

Адаптивная система терминального управления

Иллюстрации

Показать все

Реферат

Изобретение относится к области автоматического управления и может быть использовано при управлении динамическими объектами.

Известна система управления (см. Крутько П.Д. Вариационные методы синтеза систем с цифровыми регуляторами. М.: Сов Радио, 1967. - с.421, рис.50), содержащая последовательно соединенные объект управления, блок датчиков углов и акселерометров, дискретный фильтр Калмана, а также исполнительные органы, основной контур регулирования и полную модель объекта (с учетом управляющих воздействий), связанную с необходимостью идентификации всех параметров модели и коэффициентов при управляющих воздействиях.

Известна система управления (см. Самонастраивающие системы. Справочник / Под ред. П.И.Чинаева. Киев.: Наукова думка, 1969. - с.403), содержащая объект управления, выходом соединенный с первым входом параллельного корректирующего устройства и с первым входом - первого сумматора, выход которого соединен с входом блока настройки параметров модели, выходом связанного с первым входом блока модели, выход блока модели соединен со вторым входом первого сумматора и с входом блока подстройки системы, параллельное корректирующее устройство, своим выходом соединенное с первым входом второго сумматора, второй вход которого соединен с выходом выходного фильтра, выход второго сумматора соединен с первым входом последовательного корректирующего устройства, выходом соединенного с входом объекта управления и вторым входом блока модели, а блок подстройки системы своими выходами соединен со вторыми входами входного фильтра, последовательного и параллельного корректирующих устройств.

Известна также адаптивная система управления с прогнозированием (см. Патент США №4358822, кл. G05B 13/00, 1981), содержащая автоматический оператор, который может быть подключен к первой цепи, включающий в себя последовательно соединенные объект управления, сенсор, первый блок расчета, или второй цепи, включающей в себя последовательно соединенные драйвер-блок, блок управления и блок идентификации, который имеет последовательно соединенные блок задержки и второй блок расчета, выходы первой и второй цепей через устройство определения ошибки соединены с входом адаптивного механизма обратной связи, выход которого соединен с третьими входами второго блока расчета и блока управления, а четвертый вход последнего соединен с его выходом и входами объекта управления и блока идентификации, на вторые входы второго блока расчета и блока управления поступают измеряемые сигналы возмущений, причем на первые входы поступают соответственно сигналы разностного вектора выхода объекта управления и вектора, составляющими которого являются векторы выхода объекта управления, возмущения и управления, а на второй вход драйвер-блока поступает измеренный вектор выхода объекта управления.

Известна также адаптивная система с прогнозированием (см. Авторское свидетельство СССР №923293, кл. G05B 13/02, 1982), содержащая последовательно соединенные объект управления, блок датчиков угла и акселерометров, дискретный фильтр Калмана, блок модели свободного движения объекта управления, квадратор, накапливающий сумматор и блок численного дифференцирования, первым выходом соединенный с первым входом делимого блока деления, а вторым выходом - со вторым входом (делителя) того же блока деления, выход которого соединен с исполнительными органами, а выход последних - с входом объекта управления. Известная система реализует оптимальный по дискретному аналогу критерия обобщенной работы алгоритм управления, определяемый моделью свободного движения объекта управления. Для решения модели свободного движения объекта управления используются в каждом µ-ом моменте формирования управления оценки значений координат и параметров объекта управления. Значения нестационарных параметров объекта управления не используются, что приводит к неудовлетворительному качеству переходного процесса.

Наиболее близкой к изобретению по технической сущности является адаптивная система управления (см. Авторское свидетельство СССР №1646411, G05B 13/02, зарегистрировано 03.01.91 без права публикации для общего пользования), используемая преимущественно для управления движением летательных аппаратов и содержащая последовательно соединенные накапливающий сумматор, исполнительные органы, объект управления, блок датчиков углов и акселерометров, дискретный фильтр Калмана, блок модели свободного движения объекта управления, блок преобразования в частную производную от функции состояния системы, блок вычисления фундаментальной матрицы системы, матричный умножитель, выход которого соединен с входом накапливающего сумматора, а также блок преобразования в частную производную от целевой функции, вход которого соединен с входом блока преобразования в частную производную от функции состояния системы и с выходом блока модели свободного движения объекта управления, а выход - с вторым входом матричного умножителя.

Недостатком известной системы является ограниченная область практического применения, обусловленная тем, что известная система работает в режиме стабилизации, т.е. компенсации начальных угловых отклонений, а также угловых отклонений объекта управления от его номинальных (программных) значений.

Задачей изобретения является расширение области практического применения известной системы за счет решения задач терминального управления.

Сущность изобретения заключается в том, что в адаптивную систему управления, содержащую последовательно соединенные накапливающий сумматор, исполнительные органы, объект управления, блок датчиков углов и акселерометров, дискретный фильтр Калмана, блок модели свободного движения объекта управления, блок преобразования в частную производную от функции состояния системы, блок вычисления фундаментальной матрицы системы, матричный умножитель, выход которого соединен с входом накапливающего сумматора, а также блок преобразования в частную производную от целевой функции, вход которого соединен с входом блока преобразования в частную производную от функции состояния системы и с выходом блока модели свободного движения объекта управления, а выход с вторым входом матричного умножителя, введены последовательно соединенные второй блок преобразования от функции состояния системы, второй блок вычисления фундаментальной матрицы системы, второй матричный умножитель, векторный сумматор, выходом соединенный с исполнительными органами, а вторым входом - с выходом накапливающего сумматора, вход второго блока преобразования в частную производную от функции состояния системы соединен с выходом блока модели свободного движения объекта управления, входом первого блока преобразования в частную производную от функции состояния системы и входом блока преобразования в частную производную от целевой функции и последовательно соединенные блок матрицы весовых коэффициентов терминального члена оптимизируемого функционала и третий матричный умножитель, причем выход третьего матричного умножителя соединен с вторым входом второго матричного умножителя, блока вектора коэффициентов конечного состояния объекта управления, выходом соединенного с вторым входом третьего матричного умножителя, а также запоминающего элемента, ключа и блока запуска, выход которого соединен с вторым управляющим входом ключа и вторым скалярным входом дискретного фильтра Калмана, первый вход ключа соединен с выходом запоминающего элемента, а выход - с скалярным входом блока модели свободного движения объекта управления и скалярным входом накапливающего сумматора.

Технический результат расширения области практического применения известной системы достигается за счет дополнительной возможности решения задач терминального управления.

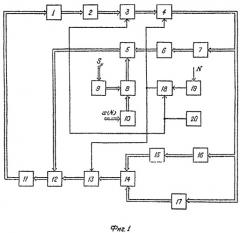
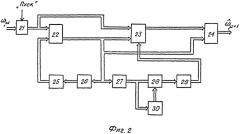
Сущность изобретения поясняется чертежом, где представлены на фиг.1 - блок-схема адаптивной системы терминального управления, а на фиг.2 - дискретный фильтр Калмана, фиг.3 - блок прогнозирующей модели, фиг.4 - блок вычисления фундаментальной матрицы системы, фиг.5 - блок преобразования в частную производную от целевой функции, фиг.6 - блок преобразования в частную производную от функции состояния системы, фиг.7 - графики управления и угловых скоростей вращения объекта.

Адаптивная система терминального управления содержит объект управления 1, блок 2 датчиков углов, угловых скоростей и акселерометров, имеющих цифровой выход, дискретный фильтр Калмана 3, блок 4 модели свободного движения объекта управления, второй матричный умножитель 5, второй блок 6 вычисления фундаментальной матрицы системы, второй блок 7 преобразования в частную производную от функции состояния системы, третий матричный умножитель 8, блок 9 матрицы весовых коэффициентов терминального члена оптимизируемого функционала, блок 10 вектора коэффициентов конечного состояния объекта управления, исполнительные органы 11, на которые управляющие сигналы поступают в цифровой форме, векторный сумматор 12, накапливающий сумматор 13, первый матричный умножитель 14, первый блок 15 вычисления фундаментальной матрицы системы, первый блок 16 преобразования в частную производную от функции состояния системы, блок 17 преобразования в частную производную от целевой функции, ключ 18, запоминающий элемент 19, блок 20 запуска (кнопку «Пуск»).

В адаптивной системе терминального управления последовательно соединены исполнительные органы 11, объект управления 1, блок 2 датчиков углов, угловых скоростей и акселерометров, дискретный фильтр Калмана 3, блок 4 модели свободного движения объекта управления, первый блок 16 преобразования в частную производную от функции состояния системы, первый блок 15 вычисления фундаментальной матрицы системы, первый матричный умножитель 14, накапливающий сумматор 13, векторный сумматор 12, а также последовательно соединены второй блок 7 преобразования в частную производную от функции состояния системы, второй блок 6 вычисления фундаментальной матрицы системы, второй матричный умножитель 5, выход которого соединен с вторым входом векторного сумматора 12. Вход второго блока 7 преобразования в частную производную от функции состояния системы соединен с выходом блока 4 модели свободного движения объекта управления, с входом первого блока 16 преобразования в частную производную от функции состояния системы и входом блока 17 преобразования в частную производную от целевой функции. Выход блока 9 матрицы весовых коэффициентов терминального члена оптимизируемого функционала соединен с первым входом третьего матричного умножителя 8, второй вход которого соединен с выходом блока 10 вектора коэффициентов конечного состояния объекта управления. Выход третьего матричного умножителя 8 соединен с вторым входом второго матричного умножителя 5. Выход блока 20 запуска соединен с вторым управляющим входом ключа 18 и вторым скалярным входом дискретного фильтра Калмана 3. Первый вход ключа 18 соединен с выходом запоминающего элемента 19, а выход - с скалярным входом блока 4 модели свободного движения объекта управления и с скалярным входом накапливающего сумматора 13.

Дискретный фильтр Калмана 3 содержит ключ 21, блок 22 расчета оценки экстраполированного значения вектора состояния γ ^ ( μ + 1 / μ ) , блок 23 расчета экстраполированного априорного значения N(µ+1/τ), блок 24 расчета оценки вектора задержки 26, блок 27 расчета корреляционной матрицы ошибок экстраполяции P[µ+1/µ), блок 28 расчета корреляционной матрицы ошибок фильтрации P(µ+1/µ+1), блок 29 умножения, регистр с перезаписью информации 30. Дискретный фильтр Калмана реализован в виде известного устройства (см. АС СССР №1179268, Кл. G05B 13/02, 15.09.1985, бюл. №34).

Блок 4 модели свободного движения объекта управления разработан для конкретного объекта, заданного уравнениями (20). Блок модели свободного движения объекта управления раскрыт до уровня известных функциональных элементов и содержит перемножители 31-33, 37-39, сумматор 40, регистры для хранения начальных условий 35, 41, 43, регистры для хранения информации на N тактов 36, 42, 44.

Блоки 6 и 15 вычисления фундаментальной матрицы системы представляют собой цифровое вычислительное устройство, состоящее из сумматора 45, накапливающего сумматора 46, n блоков матричного умножения 47 i ( i = 1, n ¯ ) . Число n выбирается из условия обеспечения требуемой точности вычисления фундаментальной матрицы системы.

Для пояснения вопроса о выборе числа n блоков матричного умножения 47_i, рассмотрим систему дифференциальных уравнений (см. Гантмахер Ф.Р. Теория матриц. М.: Наука, 1976, с.430)

d X d t = P ( t ) X ,   ( 1 )

где P(t)=||P_ik||^m - непрерывная матричная функция в некотором интервале (t₀,T) изменения аргумента t.

Используем метод последовательного приближения для определения нормированного решения системы (1), т.е. решения, образующегося в единичную матрицу при t=t₀. Последовательные приближения X_k(k=0,1,2,…) будем находить из рекуррентных соотношений

d X k d t = P ( t ) X k − 1   ( k = 1,2, … ) ,   ( 2 )

выбирая в качестве приближения Х₀ единичную матрицу Е.

Полагая X_k(t₀)=Е(k=0,1,2,…), запишем выражение для X_k - члена в виде

X k = E + ∫ t 0 t P ( t ) X k − 1 d t ( k = 1,2, … ) .   ( 3 )

Таким образом, например, для k=2 имеем матричный ряд

X 2 = E + ∫ t 0 t P ( t ) d t + ∫ t 0 t P ( t ) d t ∫ t 0 t 1 P ( t 1 ) d t 1 … ,   ( 4 )

а X_k - член ряда (3) (k=0,1,2,…) есть сумма первых (k+1) - членов матричного ряда

X k = E + ∫ t 0 t P ( t ) d t + ∫ t 0 t P ( t ) d t ∫ t 0 t P ( t 1 ) d t 1 + … + ∫ t 0 t P ( t ) d t … ∫ t 0 t P ( t k − 1 ) d t k − 1 .   ( 5 )

Для того, чтобы доказать, что этот ряд абсолютно и равномерно сходится в любой замкнутой части интервала (t₀,T), построим мажорантный ряд. Определим неотрицательные функции q(t) и h(t) в интервале (t₀,T)

{ q ( t ) = max [ | P 11 ( t ) | , | P 12 ( t ) | , … , | P m m ( t ) | ] , h ( t ) = | ∫ t 0 t q ( t ) d t | . ,   ( 6 )

Каждый из m² скалярных рядов, на которые распадается матричный ряд (5), мажорируется рядом вида

1 + h ( t ) + m h 2 ( t ) 2 ! + m 2 h 3 ( t ) 3 ! + … ,   ( 7 )

общий член которого имеет вид.

m n − 1 h n ( t ) n ! .   ( 8 )

Если задана точность вычисления фундаментальной матрицы системы (ФМС) - ε, а также известно численное значение мажорирующей функции h(t) на заданном интервале (t₀,T) и порядок системы дифференциальных уравнений - m, описывающих объект управления, тогда решая неравенство (9)

ε ≥ m n − 1 h n n ! ,   ( 9 )

нетрудно определить число членов n матричного ряда (5), которое необходимо учитывать для достижения заданной точности ε.

Блоки 7 и 17 преобразования в частную производную от функции состояния системы для объекта управления (20), рассмотренном в упоминаемом примере, реализуют функции

Y в ы х = ∂ F ( ⋅ ) ∂ x = ∂ F ∂ ω = [ 0 − A ω 3 − A ω 2 A ω 3 0 A ω 1 ] .   ( 10 )

Блок 7 представлен на фиг.5, где 48 - усилитель с коэффициентом усиления А, входом соединенного с первым входом блока 7, а выходом - с шестым выходом блока 7; 49 - инвертирующий усилитель с коэффициентом А, выход которого соединен с вторым входом блока 7, а выход - с третьим выходом блока 7; 50 - усилитель с инвертирующим и неинвертирующим выходами с коэффициентом усиления А. Входной сигнал ω₁ поступает на первый вход блока 7, с шестого выхода которого снимается сигнал, равный Aω₁. Входной сигнал ω₂ поступает на второй вход блока 7, с третьего выхода которого снимается сигнал, равный Аω₂. Входной сигнал ω₃ поступает на третий вход блока 7, с второго и четвертого выходов которого снимаются сигналы, равные Аω₃ и Аω₃ соответственно. С выходов 1, 7, 8, 9 блока 7 снимаются сигналы, равные нулевому значению «0».

Блок 16 преобразования в частную производную от целевой функции реализует функцию, соответствующую частной производной от целевой функции Н(х,u) в виде

y в ы х 16 = d H d x | x = y в х 16 = 2 [ ω 1 , ω 2 , ω 3 ] .   ( 11 )

Для целевой функции H(·) вида (11) блок 16 может быть выполнен в виде устройства, изображенного на фиг.5, где 51, 52, 53 - умножители на два.

Система работает следующим образом.

Перед началом работы в запоминающий элемент 19 вводится параметр N, характеризующий требуемую длительность процесса управления.

На матричный вход блока 10 подается значение компонента вектора x ¯ ( N ) требуемого конечного положения объекта управления 1, а на матричный вход блока 9 подаются значения матрицы весовых коэффициентов SS₁₁, SS₂₂, …, SS_mn терминального члена оптимизируемого функционала.

Работа системы начинается по сигналу «Пуск», поступающему с выхода блока 20. По этому сигналу открывается ключ 18 и на скалярные входы блоков 4 и 13 поступает значение параметра N, определяющий конечный момент времени процесса управления и текущего времени. Этим же сигналом запускается дискретный фильтр Калмана 3, который переходит в режим решения и формирует сигналы, соответствующие оценкам значений углов, угловых скоростей и линейных ускорений объекта 1 управления. Эти сигналы поступают на вход блока 4 модели свободного движения объекта управления, который в ускоренном времени моделирует свободное (неуправляемое) движение объекта управления от текущего µ до конечного N момента времени при известных начальных условиях, равным оценкам углов, угловых скоростей и линейных ускорений. Информация о прогнозируемых коэффициентах с выхода блока 4 поступает на входы блоков 7 и 17 преобразования в частную производную от функции состояния системы, а также на вход блока 16 преобразования в частную производную от целевой функции.

Блок 7 реализует функцию

y в ы х 7 = ∂ F ∂ x | x = x μ м = F ˙ x μ м ,   ( 12 )

где F(x,u) - правая часть дифференциального уравнения (1).

Блок 16 реализует функцию, соответствующую частной производной от целевой функции в виде

y в ы х 16 = ∂ N ∂ x | x = x μ м = H ˙ x μ м ,   ( 13 )

где Н(х,u) - целевая функция критерия оптимальности.

С выхода блока 7 сигнал, пропорциональный вектору частных производных от функции состояния системы, поступает на вход блока 6 вычисления фундаментальной матрицы системы, который производит вычисление фундаментальной матрицы системы согласно следующего выражения

y в ы х 15 = [ X ( τ , t ) ] T = [ E + ∑ l = 1 n ( 1 l ! ∏ i = 1 l ∑ j = μ n ∂ F ∂ x j м ) ] T ,   ( 14 )

где Е - единичная матрица; Т - знак транспонирования.

Одновременно с вычислением фундаментальной матрицы системы в блоке 6 производится вычисление фундаментальной матрицы системы, входящей в терминальный член оптимизируемого функционала. Для этого сигнал, пропорциональный вектору частных производных от функции состояния системы, поступает на вход блока 15, который производит вычисление фундаментальной матрицы системы согласно выражению

Сигнал с выхода блока 6 вычисления фундаментальной матрицы системы поступает на первый вход второго матричного умножителя, на второй вход которого поступает сигнал, пропорциональный вектору конечного (требуемого) состояния объекта управления с соответствующими весовыми коэффициентами, который формируется в третьем блоке матричного умножения в результате матричного умножения матрицы весовых коэффициентов терминального члена оптимизируемого функционала на вектор конечного (требуемого) состояния объекта управления. Сигналы, пропорциональные весовым коэффициентам матрицы терминального члена оптимизируемого функционала и вектору конечного (требуемого) состояния объекта управления, поступают соответственно на первый и второй входы третьего матричного умножителя.

Сигналы с выхода блока 15 вычисления фундаментальной матрицы системы и блока 16 преобразования в частную производную от целевой функции критерия оптимальности подаются соответственно на первый и второй входы первого матричного умножителя 14, на выходе которого получим результат умножения

y в ы х 14 = H x μ м ⋅ [ E + ∑ l = 1 n ( 1 l ! ∏ i = 1 l ∑ j = μ l ∂ F ∂ x j м ) ] T .   ( 16 )

Сигнал с выхода первого матричного умножителя 14 y_вых14 поступает на вход накапливающего сумматора 13, выходной сигнал которого имеет вид

y в ы х 13 = − ∑ r = μ N ∂ H ∂ x μ м { ∑ l = 1 n [ 1 l ! ∏ i = 1 l ∑ j = μ r ∂ H ∂ x μ м ] + E } T .   ( 17 )

С выхода накапливающего сумматора 13 сигнал y_вых13 поступает на второй вход векторного сумматора 12, на первый вход которого подается сигнал с выхода матричного умножителя вида

y в ы х 5 = − [ E + ∑ l = 1 n ( 1 l ! ∏ i = 1 l ∑ j = 1 l ∂ F ∂ x j м ) ] × [ S S 11 x 1 , S S 22 x 2 , … , S S n n x n ] T .   ( 18 )

С выхода векторного сумматора 12 управляющий сигнал y_вых12

y в ы х 12 = − [ E + ∑ l = 1 n ( 1 l ! ∏ i = 1 l ∑ j = 1 l ∂ F ∂ x j м ) ] × [ S S 11 x 1 , S S 22 x 2 , … , S S n n x n ] T − − K ⋅ ∑ r = μ N ∂ H ∂ x r м [ E + ∑ l = 1 n ( 1 l ! ∏ j = 1 l ∂ F ∂ x j м ) ] T   ( 19 )

поступает на исполнительные органы 11, которые, воздействуя на объект управления, переводят его из начального состояния в конечное (требуемое) к заданному моменту времени.

Пример. Пусть движение твердого тела (ТТ) с одной осью симметрии (см. Сю Д., Мейер А. Современная теория автоматического управления и ее применение. М.: Машиностроение, 1972, с.544) описывается уравнениями

{ ω ˙ 1 + A ω 2 ω 3 = u 1 , ω 1 | t = 0 = ω 1 ( 0 ) ; ω ˙ 2 − A ω 1 ω 3 = u 2 , ω 2 | t = 0 = ω 2 ( 0 ) ; ω ˙ 3 = u 3 , ω 3 | t = 0 = ω 3 ( 0 ) ,   ( 20 )

где ω₁, ω₂, ω₃ - угловые скорости; u₁, u₂, u₃ - управляющие ускорения;

А - приведенный момент инерции.

Требуется составить алгоритм терминального управления по переводу объекта (20) к моменту времени Т из состояния ω ¯ i ( t 0 ) = ω i ( 0 )   ( i = 1,3 ¯ ) в состояние ω ¯ i ( T ) ( i = 1,3 ¯ ) , оптимального по квадратичному критерию

I = ∑ i = 1 3 S S i i ω i ( T ) + ∫ t 0 T ( ∑ i = 1 3 ω i 2 + u i 2 ) d t ,   ( 21 )

где S S i i ( i = 1,3 ¯ ) - диагональные элементы матрицы весовых коэффициентов терминального члена оптимизируемого функционала.

Один из законов оптимального управления, полученных градиентным методом на основе прогнозирующей модели (см. Детистов В.А., Таран В.Н. Синтез оптимального управления градиентным методом на основе прогнозирующей модели. Автоматика и телемеханика 1990 №10. С.46-56) для объекта (1), имеет вид

u ˜ = − ∫ t T G * ( s , t ) ω ( s ) d s ,   ( 22 )

где s - ускоренное время; ω(s)=[ω₁(s),ω₂(s),ω₃(s)] - вектор прогнозируемого состояния системы; * - знак транспонирования; u=[u₁,u₂,u₃] - вектор управляющих ускорений системы; G(s,t) - фундаментальная (переходная) матрица системы.

Для объекта (20) выражение для фундаментальной матрицы найдено в аналитической форме

G ( s , t ) = = [ cos x ( t ) − sin x ( t ) − ∫ t t K [ A ω 2 ( τ ) cos ( x ( t ) − x ( τ ) ) + A ω 1 ( τ ) sin ( x ( t ) − x ( τ ) ) ] d τ sin x ( t ) cos x ( t ) − ∫ t t K [ A ω 2 ( τ ) sin ( x ( t )