Способ сжатия изображения

Способ сжатия изображения

Иллюстрации

Показать все

Реферат

Изобретение относится к области обработки цифровых сигналов и может быть использовано для сжатия (компрессии) статических и динамических изображений, то есть преобразования данных с целью уменьшения их объема, как без потерь, так и с потерями части информации.

В современном мире наблюдается лавинообразный рост медиа-контента, поэтому сжатие данных является актуальным направлением научных исследований.

Известны способы сжатия данных без потерь, основанные на использовании статистической информации (повторении, автокорреляции), и сжатие с потерями, основанное на удалении избыточной (не существенной или не критической) информации (Ватолин Д., Ратушняк А., Смирнов М., Юкин В. Методы сжатия данных. М.: Диалог - МИФИ, 2003; Сэломон Д. Сжатие данных, изображений и звука. М.: ТЕХНОСФЕРА, 2004). Применяют данные способы как по отдельности, так и в различных сочетаниях. Сжатие без потерь применяют к двухуровневым (однобитным), многоуровневым и полноцветным изображениям. Наиболее распространены реализации алгоритмов, ориентированных на сжатие растровых изображений без потерь, GIF (S.Blackstock. LZW and GIF explained. http://www.martinreddy.net/gfx/2d/GIF-comp.txt) (статические и динамические изображения) и PNG (PNG home page. http://www.libpng.org/pub/png/png.html). В основе данных способов лежат словарные кодирования на основе модификации преобразования Хаффмана и LZ77, LZ78 (LZW - Lempel, Ziv, Welch).

Известен фрактальный способ сжатия изображений, основанный на том, что изображение можно представить более компактно с помощью коэффициентов системы итерируемых функций (D.Saupe, R.Hamzaoui, H.Hartenstein. Fractal image compression - An introductory overview, in: Fractal Models for Image Synthesis, Compression, and Analysis, D.Saupe, J.Hart (eds.), ACM SIGGRAPH'96 Course Notes).

Известны способы, в которых из изображений, применяя метод «brush fire» (лесной пожар), формируют скелет многоугольника толщиной 1-2 пикселя, являющийся диаграммой Вороного. К сложностям практической реализации таких методов относится: формирование корректного скелета в виде связного графа (Скиена С. Алгоритмы. Руководство по разработке. - 2-е изд. Пер. с англ. - СПб.: БХВ-Петербург, 2011).

Известен интерполяционный способ сжатия телевизионного сигнала (патент РФ №2131172, дата приоритета 10.12.1996, МПК H04N 5/335, опубликовано 27.05.1999 г.), в основе которого лежит искусственное исключение фрагментов сигналов строк и их восстановление с помощью интерполяции по фрагментам не исключенных частей строк, что позволит сократить избыточность телевизионного сигнала.

Известен способ сжатия с потерями на базе дискретно-косинусного преобразования (ДКП), предназначенный для статических и динамических изображений, который является наиболее близким по совокупности существенных признаков к заявляемому способу и принят в качестве прототипа (Стивен Смит. Цифровая обработка сигналов. Практическое руководство для инженеров и научных работников. Пер. с англ. Линовича А.Ю., Витязева С.В., Гусинского И.С. - М.: Додека-XXI, 2011, стр.548). В этом способе распространенный формат JPEG использует для сжатия дискретно-косинусное преобразование (ДКП) с последующим модифицированным преобразованием Хаффмана. Основой JPEG-сжатия является получение пространственного спектра изображения с последующим исключением некоторой части спектральных компонентов, позволяющее впоследствии восстановить изображение в достаточном качестве. Полученный спектр изображения в силу того, что он может содержать значительное число повторяющихся отдельных элементов и цепочек, эффективно сжимают.

При JPEG-сжатии пространственный спектр получают путем двумерного ДКП матрицы изображения U размером M×N в соответствии с выражением:

B = p q α p α q ∑ m = 0 M − 1 ∑ n = 0 N − 1 A m n cos π ( 2 m + 1 ) p 2 M cos π ( 2 n + 1 ) q 2 N ,             ( 1 )

где 0≤p≤M-1, 0≤q≤N-1;

α p = { 1 M ,   е с л и   p = 0 ; 2 M ,   е с л и   1 ≤ p ≤ M − 1 ; α q = { 1 N ,   е с л и   p = 0 ; 2 N ,   е с л и   1 ≤ p ≤ N − 1.

Значения B_pq называют ДКП матрицы U.

Обратное ДКП реализуется согласно выражениям:

U = m n α p α q ∑ p = 0 M − 1 ∑ q = 0 N − 1 α p α q B p q cos π ( 2 m + 1 ) p 2 M cos π ( 2 n + 1 ) q 2 N ,             ( 2 )

где 0≤m≤M-1, 0≤n≤N-1;

α p = { 1 M ,   е с л и   p = 0 ; 2 M ,   е с л и   1 ≤ p ≤ M − 1 ; α q = { 1 N ,   е с л и   p = 0 ; 2 N ,   е с л и   1 ≤ p ≤ N − 1.

В реализации алгоритма JPEG-сжатия исходное изображение после преобразования из цветового пространства RGB в YCrCb разделяется на квадратные блоки размером 8×8 или реже 16×16, для которых производится ДКП. Коэффициенты дискретных косинусных преобразований фильтруются с удалением некоторых (в зависимости от степени сжатия) значений, квантируются, а затем кодируются при помощи модифицированного преобразования Хаффмана. В результате этих преобразований получается массив данных, существенно меньший по размеру, чем исходное изображение, содержащий информацию, по которой можно восстановить исходное изображение с некоторой, в зависимости от степени сжатия, точностью. Восстановление изображения происходит в обратной последовательности: сначала сжатое изображение подвергается обратному модифицированному преобразованию Хаффмана, затем обратному ДКП. Недостатком JPEG-сжатия на основе ДКП является потеря целостности изображения, возникающая в результате специфических артефактов «блочности» (контрастное выделение областей 8×8 или 16×16) в восстановленном изображении. Артефакт «блочности» является следствием отсутствия «гладкой сшивки» областей, выделенных для ДКП. К следующему недостатку можно отнести потерю контрастности, что проявляется в «размытии» границ между различными объектами изображения и является следствием фильтрации (удаления при сжатии) высокочастотных составляющих. Артефакт «размытия» допустим в фотографических изображениях, но в некоторых видах изображения, например космических снимках, изображениях для печати, где необходимо сохранить контраст, «размытие» недопустимо. При сжатии без потерь в формате JPEG возможно сохранение контрастности границ объектов, при этом размер сжатого изображения остается достаточно большим, что тоже является недостатком. JPEG формат не обеспечивает эффективное сжатие изображений, содержащих большие пространства одного цвета или плавного градиента.

Заявляемое изобретение устраняет потерю целостности изображения, повышает эффективность сжатия изображений, содержащих большие участки одного тона или градиента (цвета, яркости), сохраняет контрастность границ между различными объектами изображения.

Указанная задача решается за счет того, что изображения (статические или динамические) рассматриваются как дискретные полевые структуры, полное численное описание которых (то есть значения во всех дискретных точках по координатам пространства и (или) времени) можно определить путем решения уравнений Лапласа или Пуассона, располагая исходными данными в качестве граничных (краевых) условий.

Сущность изобретения заключается в том, что при сжатии изображения (статического или динамического) происходит отыскание массива данных, названного в рамках изобретения «паттерн», являющегося массивом граничных условий и позволяющего с заданной степенью точности, путем численного решения уравнений Лапласа или Пуассона, восстановить исходное изображение. Полученный паттерн содержит некоторое (в большинстве случаев достаточно значительное) число повторяющихся элементов и последовательностей, что позволяет эффективно сжимать паттерн стандартными методами, например на основе модификации преобразования Хаффмана, или LZ78, или арифметического кодирования. В случае применения для формирования паттерна и восстановления изображения уравнения Пуассона, подлежит определению функция правой части, правильный подбор которой может в значительной мере способствовать сжатию изображения.

Предлагаемый способ отличается от способов JPEG тем, что в нем для сжатия изображения используется не получение пространственного спектра, а формирование краевых условий для решения дифференциальных уравнений (Пуассона или Лапласа), позволяющих восстановить изображение. При этом может быть учтен и пространственный спектр, в случае если для формирования паттерна и восстановления изображения выбирают уравнения Пуассона, и если в правой части уравнения Пуассона содержится функция (или функциональный ряд), позволяющая учесть пространственный спектр. Таким образом, предлагаемый способ позволяет при сохранении малого числа низкочастотных составляющих сохранить мелкие (высокочастотные) детали изображения за счет паттерна граничных условий. Применение дифференциальных уравнений второго порядка позволяет отслеживать изменение изменений (амплитуды при переходе от точки к точке (от пикселя к пикселю), описывающей яркость, насыщенность или другую характеристику изображения в зависимости от выбранной цветовой схемы) и сохранять только те значения, в которых изменения изменений являются существенными, т.е. превосходят численно указанное значение, определяющее степень сжатия. Таким образом, в отличие от JPEG-преобразования для сжатия и восстановления изображения рассматривается не пространственный спектр изображения, а его пространственная «дифференциальная структура», т.е. наличие и численная величина изменения изменений, что позволяет эффективно сжимать области градации (цвета, яркости и т.д.) и в некоторых случаях производить более эффективное сжатие по сравнению с JPEG.

Изображение (статическое или динамическое) рассматривается как пространственно-неразделимая, многомерная полевая структура. В случае статического изображения - двумерная (аналог плоскопараллельного поля), в случае динамического изображения - трехмерная (аналог трехмерного поля или плоскопараллельного поля, изменяющегося во времени). Таким образом, изображение можно описать уравнениями в частных производных.

Для двумерного случая:

- уравнением Лапласа:

∂ 2 U ∂ x 2 + ∂ 2 U ∂ y 2 = 0                         ( 3 )

- уравнением Пуассона:

∂ 2 U ∂ x 2 + ∂ 2 U ∂ y 2 = f ( x , y )                     ( 4 )

Для трехмерного случая (для динамических изображений, видеопотока):

- уравнением Лапласа:

∂ 2 U ∂ x 2 + ∂ 2 U ∂ y 2 + ∂ 2 U ∂ t 2 = 0                         ( 5 )

- уравнением Пуассона:

∂ 2 U ∂ x 2 + ∂ 2 U ∂ y 2 + ∂ 2 U ∂ t 2 = f ( x , y , t )                   ( 6 )

где использованы следующие обозначения: x, y - пространственные координаты, t - третья пространственная координата или время, U - значение амплитуды в компоненте выбранного цветового пространства изображения, f - функция, связывающая закономерности изменения изображения с изменением пространственных координат.

При сжатии изображения решается обратная задача к решению уравнений (3)-(6), то есть производится отыскание граничных условий. Такой массив граничных условий в рамках данного изобретения именуется паттерном изображения или кратко паттерном. В случае выбора уравнений Пуассона также подлежит отысканию функция f. После формирования паттерна к нему может быть применен стандартный способ сжатия, применяемый к массивам данных, содержащих значительное число повторяющихся символов, например, на основе модификации преобразования Хаффмана, или LZ78, или арифметического кодирования.

Разархивирование сжатого изображения сводится к извлечению паттерна (и функции f в случае уравнений Пуассона) из архива (на основе ранее выбранного способа архивации), далее решение уравнений Лапласа или Пуассона производится на основании известных краевых условий, например, методом конечных разностей.

Заявляемый способ иллюстрируется чертежами, где изображены:

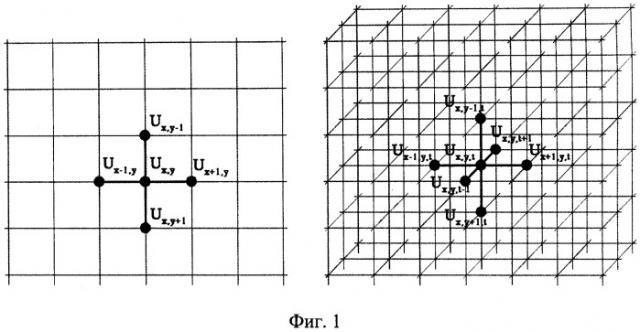
фиг.1 - возможные варианты выбора шаблонов дифференцирования для двухмерного (x,y) и трехмерного (x,y,t) пространств;

фиг.2 - исходное изображение черно-белое с градациями серого от 0 до 255, длина массива изображения 152100 байт. Изображение содержит мелкие и крупные пространственные элементы;

фиг.3 - визуализация массива граничных условий, названного в рамках способа «паттерн», паттерн содержит 42639 элементов граничных условий (отличных от нуля) и 109461 нулей;

фиг.4 - результат восстановления изображения за 20 итераций, по паттерну (фиг.3), без предильтрации;

фиг.5 - результат восстановления изображения за 20 итераций, по паттерну (фиг.3), с применением предфильтрации;

фиг.6 - графики суммы невязок по всем точкам решетки, узлами которой являются пиксели изображения. По вертикальной оси сумма невязки, по горизонтальной номер итерации. Отображены графики для случая восстановления изображения: с применением предфильтрации; без применения предфильтрации. Очевидно, что применение предфильтрации позволяет многократно ускорить сходимость итерационного процесса, т.е. скорость восстановления изображения;

фиг.7 - исходное полноцветное изображение 800×654, число байт в 24-битной палитре - 1353600;

фиг.8 - паттерн, полученный для цветовой палитры RGB, число значащих байт - 307358, нулей - 1046242. Отношение числа значащих элементов (байт) паттерна к объему исходного изображения (байт): 0,2271;

фиг.9 - восстановленное изображение по паттерну (Фиг.8), стоит обратить внимание на то, что несмотря на значительное сокращение объема информации мелкие (высокочастотные) детали (фактура скатерти) сохранились;

фиг.10 - паттерн, полученный для цветовой палитры YCrCB, число значащих байт - 141449, нулей - 1212151, при примерно одинаковом качестве восстановленных изображений (Фиг.9 и Фиг.11). Отношение числа значащих элементов (байт) паттерна к объему исходного изображения (байт): 0,1045. Число значащих элементов в 2,17 раза меньше, чем в паттерне на Фиг.8;

фиг.11 - восстановленное изображение по паттерну (Фиг.10). Стоит обратить внимание на то, что несмотря на значительное сокращение объема информации мелкие (высокочастотные) детали (фактура скатерти) сохранились;

фиг.12 - одно из стандартных тестовых изображений (The USC-SIPI Image Database http://sipi.usc.edu/database/), исходное изображение - слева (размер, в формате bmp 24-bit, 196608 байт), восстановленное - справа;

фиг.13 - паттерн для изображения (фиг.12), число исключенных элементов (нулей) 134831;

фиг.14 - одно из стандартных тестовых изображений (в формате bmp 24-bit), размер 786432 байт;

фиг.15 - паттерн для изображения (фиг.14), число исключенных элементов (нулей) 535552;

фиг.16 - восстановленное изображение по паттерну (фиг.15).

Для раскрытия способа рассмотрим последовательность процедуры сжатия и процедуры восстановления изображения. Процедура сжатия на основании уравнений Лапласа состоит в отыскании граничных условий для решения уравнения в частных производных (в соответствии с выбранным ранее шаблоном). Выбор шаблона зависит от конкретной реализации предлагаемого способа. Отыскание граничных условий (паттерна) производится путем расчета значений частных производных второго порядка в каждой точке изображения с последующим вычислением разности с фактическими значениями в соответствующей точке. Полученная разность является критерием для принятия решения оставить данную точку для паттерна или исключить, численное значение критерия будет соответствовать «степени» сжатия. При нулевом значении критерия происходит сжатие без потерь. Для цветных изображений преобразование можно производить в любом заранее выбранном цветовом пространстве, например RGB или YCrCb. Преобразование производится отдельно для каждого канала цветовой палитры. В специальных исследованиях было показано, что в цветовой палитре YCrCb, для некоторых изображений, можно добиться более высокой степени сжатия, чем в палитре RGB.

Запишем всю процедуру в формальном виде для двумерного статического изображения при выбранном шаблоне (фиг.1). В общем случае шаблон может быть любой конфигурации, позволяющей эффективно решать уравнения в частных производных. Пусть двумерный массив изображения характеризуется множеством значений U_x,y, где x, y - координаты соответствующей точки. Произведем вычисление разностного значения фактической величины U_x,y, в массиве изображения, и результата решения уравнения Лапласа:

U x , y − 1 4 ( U x − 1, y + U x + 1, y + U x , y − 1 + U x , y + 1 ) = Δ U x , y

При выбранном критерии h, произведем сравнение |ΔU_x,y| (абсолютного значения) разности с величиной h, если условие (|ΔU_x,y|≥h) истинно, то U_x,y будет частью паттерна, если ложно, то U_x,y исключается из паттерна и на место U_x,y, у записывается некоторый (численный) признак (например, ноль) по которому можно будет определить, что данная точка с координатами (x,y) не является граничным условием, а требует вычисления. Очевидно, что в результате вычислений происходит переход от целочисленных значений U к значениям с плавающей точкой. Избежать этого можно заменяя операцию деления операцией поразрядного сдвига. Решение задачи на множестве целых чисел позволяет существенно ускорить процедуру формирования паттерна. При выборе практической реализации нужно учитывать условия конкретных задач и доступность вычислительных ресурсов.

Необходимо отметить, что точки, расположенные по краям изображения (для статического двумерного изображения четыре вектора), являются граничными условиями и для них описанные вычисления не применяются, возможно их непосредственное копирование в массив граничных условий или рассмотрение точек, расположенных по краям изображения, как одномерных векторов, к которым можно применить уравнения вида d 2 U d x 2 = 0 (для векторов вдоль оси X) и d 2 U d y 2 = 0 (для векторов вдоль оси Y).

В случае динамического изображения принципиальный подход остается прежним. Уравнение расчета разности будет иметь следующий вид:

U x , y , t − 1 6 ( U x − 1, y , t + U x + 1, y , t + U x , y − 1 , t + U x , y + 1, t + U x , y , t − 1 + U x , y , t + 1 ) = Δ U x , y , t

К плоскостям, ограничивающим рассматриваемую область, может быть применен вышеописанный способ формирования паттерна для двумерного изображения или непосредственное копирование в массив граничных условий.

При использовании в качестве основы для вычисления паттерна уравнения Пуассона возникает вопрос в определении правой части функции f(x,y) - для двумерного случая, f(x,y,t) - для трехмерного случая. Функцию f необходимо выбирать таким образом, чтобы рассчитываемый паттерн содержал наименьшее число элементов, являющихся граничными условиями. При этом сама функция будет определена набором коэффициентов, хранение которых может требовать значительного объема памяти. Решение можно определить как минимизацию числа граничных элементов, образующих паттерн, и коэффициентов функции f при сохранении достаточного качества восстанавливаемого изображения. Рассмотрим некоторые варианты функции f:

- плоскость: f(x,y)=ax+by+с;

- обратное дискретное косинусное преобразование (см. (2)), всего пространства изображения:

f ( x , y ) = ∑ p = 0 M − 1 ∑ q = 0 N − 1 α p α q B p q cos π ( 2 m + 1 ) p 2 M cos π ( 2 n + 1 ) q 2 N ;

- разнообразные вейвлет-функции, с помощью набора вейвлет-коэффициентов позволяющие вычислить с заданной точностью значения в пространстве изображения;

- массив дискретных значений, соответствующий средним значениям в областях, полученных разбиением изображения на прямоугольники (в двумерном случае) или параллелепипеды (в трехмерном случае).

Очевидно, что в качестве правой части могут выбираться и любые другие функции (функциональные ряды), наиболее подходящие для конкретного случая. В качестве примера рассмотрим более подробно ДКП. ДКП в зависимости от степени сжатия изображения позволяет сохранять или исключать высокочастотные («мелкие») детали, а предлагаемый способ может отлично сохранять «мелкие» детали изображения. Таким образом, можно использовать несколько низкочастотных компонент ДКП в качестве правой части уравнения Пуассона. Аналогично можно использовать вейвлет- преобразование в качестве правой части уравнения Пуассона, позволяющей учесть особенности пространственного спектра изображения.

При ограниченном числе разрядов на сохранение одного канала цветовой схемы имеется ограничение на возможные значения. Например, при восьми разрядах на каждый канал в цветовой схеме RGB допустимые значения ограничены диапазоном 0-255. Граничные значения в паттерне записываются путем копирования соответствующих значений из исходного изображения, прочие значения в паттерне заполняются заранее выбранной величиной, например нулем. Если же в точках паттерна встретится ноль, то отличить его от прочих нулей, которыми записаны точки, не являющиеся граничными условиями, будет невозможно. Для восприятия человеком градация в пределах 1/256 будет незаметной, но если необходимо иметь возможность сохранять изображение без потерь, то возникающую ошибку необходимо корректировать, для коррекции можно использовать битовую маску изображения.

В результате изложенных выше преобразований формируется паттерн, содержащий значительное число повторяющихся элементов, к такому паттерну можно эффективно применять алгоритмы сжатия на основе стандартных преобразований: Хаффмана, LZ78, арифметического кодирования.

Обратное преобразование заключается в восстановлении исходного изображения по паттерну. Наиболее очевидным решением является применение итерационного метода конечных разностей, граничными условиями для решения является паттерн. При таком подходе время вычислений для восстановления изображения в достаточно высоком качестве может быть значительным, особенно при больших размерах изображения. Поэтому в рамках рассматриваемого способа предлагается использовать предфильтрацию. Смысл предфильтрации состоит в ускорении сходимости процесса итерационных вычислений методом конечных разностей. Рассмотрим возможный вариант реализации предфильтрации, на примере двумерного изображения. Предфильтрация производится последовательно сначала в направлении Х, а затем в направлении Y или наоборот. Итак, совершим проход по первой (первой из тех, к которым применялся разностный способ формирования паттерна, крайние строки являются граничными условиями, см. выше) строке, если встречаем элемент, являющийся элементом граничного условия, запоминаем его значение и двигаемся далее, пока не встретим следующий элемент, являющийся элементом граничного условия. Зная значение двух граничных элементов, в пределах одного вектора, применяем аппроксимацию (например, линейную) для вычисления значений элементов, расположенных между ними. Таким образом, аппроксимируем все значения в пределах одной строки. Последовательно проходим все строки в направлении Х, а затем совершаем такой же проход по всем строкам в направлении Y. При проходе по строкам в направлении Y учитываем ранее полученные значения (при проходе по X) и вычисляем фактическое значение как среднее между проходом в направлении Х и Y.

Возможно добавить предфильтрующие проходы по диагоналям.

При использовании уравнений Пуассона в качестве функции, осуществляющей «предфильтрацию», можно использовать уравнение правой части совместно с описанным выше проходом в направлениях Х и Y.

Результатом такой предфильтрации является массив данных, который можно рассматривать как часть вычислений, полученную в результате выполнения некоторого итерационного приближения. Описанная выше предфильтрация позволяет существенно ускорить сходимость итерационного процесса, а значит, ускорить процесс восстановления изображения. Дальнейшие итерационные вычисления можно производить методом конечных разностей. Критерием к завершению вычислений может служить численная оценка невязки. Такой поход позволяет достаточно быстро сформировать изображение (например, на экране монитора) и последовательно, продолжая итерации и периодически обновляя изображение, повышать его визуальное качество (прогрессирующее декодирование).

Описанный способ возможно применять к динамическим (трехмерным) изображениям, используя в качестве еще одной координаты время f(x,y,t). Возможно применение способа в других многомерных изображениях, например в трехмерном телевидении, где в зависимости от реализации может быть от четырех (три пространственных и время) и более координат.

Для реализации предлагаемого способа необходимо выполнить последовательность действий, отвечающую всем признакам алгоритма.

Порядок последовательности действий способа строго определен и детерминирован.

Обобщенный алгоритм сжатия двумерного статического изображения (применяется уравнение Лапласа). В описании алгоритма изображение, паттерн - являются целочисленными, двумерными массивами значений (в узлах сетки изображения - пикселях).

1. Формируем паттерн изображения, являющийся массивом граничных условий для решения уравнений Лапласа или Пуассона при восстановлении. В случае если применяется уравнение Пуассона, производим расчет необходимых коэффициентов, однозначно описывающих правую часть уравнения Пуассона.

2. Если необходимо сохранять изображение без потерь, формируем битовую матрицу (массив), позволяющую произвести коррекцию изображения при восстановлении. Битовую маску также сжимаем, например, способом кодирования длин серий RLE.

3. Применяем к полученному паттерну стандартный способ компрессии, позволяющий эффективно сжимать данные, содержащие значительное число повторяющихся элементов.

Обобщенный алгоритм восстановления изображения:

1. Производим операцию разархивирования паттерна в соответствии со способом его упаковки. В случае необходимости производим разархивирование коэффициентов (в случае использования уравнения Пуассона) и битовой матрицы (для восстановления изображения без потерь).

2. Производим предфильтрацию, используя поученный (в пункте 1) паттерн. Целью предфильтрации является ускорение процесса сходимости итерационного процесса восстановления изображения по паттерну.

3. Производим расчет (восстановление) изображения по паттерну, используя в качестве области восстановления (массива, в котором будет получено восстановленное изображение) массив, полученный на этапе предфильтрации. Критерием окончания расчетов может быть заданное число итераций или значение невязки (контролирующее сходимость итерационного процесса).

4. В случае если необходимо восстановить изображение без потерь, производим коррекцию с помощью битовой маски.

Таким образом, предлагаемый способ устраняет потерю целостности изображения, повышает эффективность сжатия изображений, содержащих большие участки одного тона или градиента (цвета, яркости), и сохраняет контрастность границ между различными объектами изображения.

1. Способ сжатия изображения, основанный на исключении некоторой части информации, отличающийся тем, что информацию исключают из пространственной области путем численного решения дифференциальных уравнений Пуассона или Лапласа и последующей оценки различия между полученным решением и фактическими значениями в дискретных точках изображения, формируют массив граничных условий, содержащий значительное число равных элементов, который сжимают, а для восстановления изображения решают дифференциальные уравнения в частных производных Пуассона или Лапласа, используя массив граничных условий.

2. Способ по п.1, отличающийся тем, что производят предфильтрацию массива граничных условий, заполняя множество точек изображения, не принадлежащее граничным условиям, значениями функций аппроксимации, вычисленными по известным точкам граничных условий.