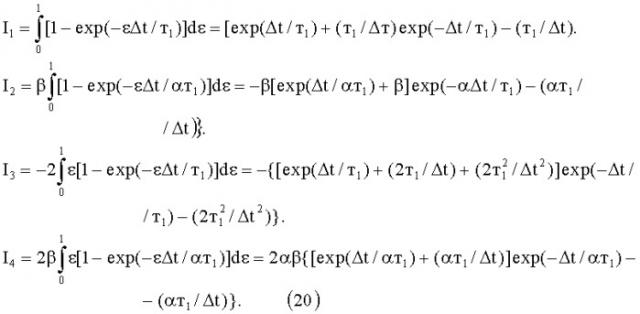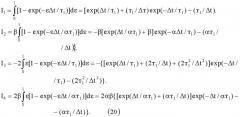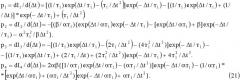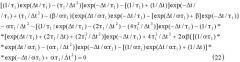Устройство для получения механической энергии

Устройство для получения механической энергии

Иллюстрации

Показать все

Реферат

Изобретение относится к физике магнетизма и может использоваться в качестве устройства, преобразующего тепловую энергию окружающей среды в механическую работу постоянно вращающегося кольца (диска) якобы без видимого притока энергии.

Как известно [1-3], согласно закону сохранения и превращения энергии невозможно построение вечных двигателей. Второе начало термодинамики [4] доказывает невозможность создания тепловых двигателей с кпд. равным единице. Основным эмпирическим положением второго начала термодинамики является невозможность создания циклически действующей машины, которая непрерывно производила бы механическую работу, полностью превращая в нее все тепло, получаемое от нагревателя. Первое начало термодинамики, определяющее превращение энергии при изменении состояния системы, следует из закона сохранения энергии, распространенного на случай механо-тепловых процессов. Для конечного изменения состояния он выражается следующей зависимостью Q=ΔU+A, где Q - количество тепла, полученное системой, ΔU - увеличение ее внутренней энергии, A - механическая работа, произведенная системой, или другая равнозначная работа, например, работа электрических (магнитных) сил.

Аналогов заявляемому техническому решению не найдено.

Целью изобретения является получение механической энергии непосредственно из тепловой энергии в магнитодинамической системе.

Заявляемое устройство для получения механической энергии, состоящее из динамически сбалансированного вращающегося кольца (диска) с осью вращения, помещенного своим краем в зазоры постоянных магнитов, причем указанное кольцо (диск) выполнено из смеси парамагнитного и диамагнитного вещества с такими концентрациями x₁ и х₂ этих ингредиентов, что выполнены условия x₁X₁-x₂|X₂|→0, x₁+x₂=1, где X₁ и X₂ - магнитные восприимчивости соответственно парамагнитного и диамагнитного веществ смеси, в течение времени пребывания любого дифференциального объема смеси dv=Sdx, где S - поперечное сечение кольца (диска), охваченного магнитным зазором, dx - дифференциальный слой кольца (диска) вдоль направления движения смеси в магнитном зазоре по оси x, равного Δt=L/ωR, где L - длина магнитного зазора вдоль оси x, ω - угловая скорость вращения кольца (диска), R - радиус кольца (диска), а также условие, что постоянная магнитной вязкости парамагнитного вещества т₁ в пять и более раз меньше постоянной магнитной вязкости диамагнитного вещества т₂; кроме того, устройство включает систему магнитного подвеса вращающегося кольца (диска) с осью вращения, снабженную элементами ее скольжения, прозрачную цилиндрическую вакуумную колбу, в которую помещены один или несколько постоянных магнитов, вращающееся кольцо (диск) с осью вращения с закрепленными на нее элементом магнитного подвеса и ротора первичного раскручивания оси вращения, съемный узел, создающий вращающееся магнитное поле, и многофазный генератор переменного тока с регулируемой частотой.

Для увеличения мощности модели в ней используется несколько эквидистантно расположенных вокруг вращающегося кольца (диска) постоянных магнитов подковообразной формы, в магнитные зазоры которых помещена кромка вращающегося кольца (диска) и которые закреплены на стенках прозрачной цилиндрической вакуумной колбы.

Для снижения потерь на трение вращающегося кольца (диска) заявляемое устройство включает систему магнитного подвеса вращающегося кольца (диска) с осью вращения, которая включает два намагниченных ферромагнитных тороида, один из которых закреплен на днище прозрачной цилиндрической вакуумной колбы, а другой является элементом магнитного подвеса, закрепленным на оси вращения, причем намагниченные по их торцам ферромагнитные тороиды соосны и обращены друг к другу одноименными магнитными полюсами.

Кроме того, для первоначального раскрута вращающегося кольца (диска) на прозрачной цилиндрической вакуумной колбе установлен съемный узел, который представляет многофазный статор, надеваемый (и снимаемый) на прозрачную цилиндрическую вакуумную колбу, электрически соединенный с выходом многофазного генератора переменного тока с регулируемой частотой, и магнитно связанный с ротором первичного раскручивания оси вращения, выполненным в виде многополюсного ферромагнитного диска, закрепленного на оси вращения, причем съемный узел установлен на цилиндрическую подставку, расположенную вместе с прозрачной цилиндрической вакуумной колбой на горизонтальной плоскости, высота которой обеспечивает оппозитное расположение многофазного статора относительно ротора первичного раскручивания оси вращения.

Достижение цели изобретения в заявляемом устройстве объясняется непрерывным во времени втягиванием вращающегося кольца (диска) в магнитный зазор постоянного магнита с некоторой силой, совпадающей с вектором скорости кольца (диска) внутри магнитного зазора и поддерживающей вращение кольца (диска) неограниченно долго за счет убывающего распределения суммарной намагниченности пара- диамагнитной смеси, из которой выполнено кольцо (диск), из-за выбора величины постоянной магнитной вязкости парамагнетика во много раз меньшей величины постоянной магнитной вязкости диамагнетика, так что в начале магнитного зазора по ходу движения в нем смеси пара- диамагнитного вещества намагниченность быстро возрастает, доходит до некоторого максимума, а затем медленно падает практически до нуля в конце магнитного зазора При этом площадь под кривой намагниченности в первой половине магнитного зазора существенно превышает площадь под кривой намагниченности во второй половине магнитного зазора при оптимальной угловой скорости вращения кольца (диска). В результате квазиадиабатического процесса намагничивания-размагничивания происходит потеря внутренней энергии кольца (диска), которое при этом охлаждается по отношению к температуре окружающей среды, а восполнение тепловых потерь осуществляется в механизме теплопроводности забором тепловой энергии из окружающей среды, что согласуется с законом сохранения и превращения энергии. В заявляемом устройстве тепловая энергия превращается в механическую в динамике вращения пара-диамагнитного кольца (диска) в присутствии пространственно локализованного магнитного поля с достаточно высокой напряженностью в магнитном зазоре постоянного магнита.

Заявляемое устройство понятно из представленных рисунков.

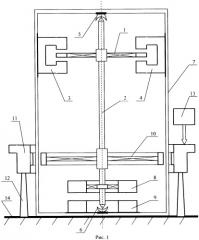
На рис.1 изображена схема заявляемого устройства, содержащего следующие элементы и узлы:

1 - кольцо (диск) из пара-диамагнитной смеси,

2 - ось вращения кольца (диска),

3 и 4 - первый и второй постоянные магниты,

5 и 6 - элементы скольжения оси вращения, закрепленные на крышке и днище прозрачной цилиндрической вакуумной колбы,

7 - прозрачная цилиндрическая вакуумная колба,

8 - первый намагниченный ферромагнитный тороид системы подвеса, закрепленный с осью вращения,

9 - второй намагниченный ферромагнитный тороид системы подвеса, закрепленный на днище корпуса 7,

10 - многополюсной ферромагнитный диск, закрепленный на оси вращения,

11 - съемный узел, создающий вращающееся магнитное поле,

12 - цилиндрическая подставка для съемного узла 11,

13 - многофазный генератор переменного тока с регулируемой частотой,

14 - горизонтальная плоскость.

На рис.2 представлены графики намагниченности дифференциальных объемов вращающегося кольца (диска) в различных сечениях магнитного зазора для парамагнитной x₁*J₁(x) и диамагнитной x₂*J₂(x) компонент смеси с учетом их концентраций x₁ и х₂, а также суммарная намагниченность смеси J_Σ(x), где 0≤x=ωRt≤L (t - текущее время), при выполнении условий x₁X₁-x₂|X₂|→0, x₁+x₂=1, а также условия т₁<<т₂, где т₁ и т₂ - постоянные магнитной вязкости соответственно парамагнитной и диамагнитной компонент смеси. Видно, что суммарная намагниченность дифференциальных объемов части вращающегося диска (кольца), расположенной в магнитном зазоре постоянного магнита, сначала быстро возрастает за счет влияния парамагнитной компоненты смеси, доходит до некоторого максимума, а затем сравнительно медленно падает практически до нуля к концу магнитного зазора (при х=L) за счет влияния диамагнитной компоненты смеси.

На рис.3 представлена развертка фрагмента заявляемого устройства, включающая магнитный зазор рабочего постоянного магнита 3 (4) и движущуюся со скоростью V=ωR вдоль оси х смесь пара-диамагнитного вещества, из которого состоит вращающееся кольцо (диск) 1 в магнитном поле H, под действием возникающей силы F_Σ, коллинеарной вектору скорости V.

На рис.4 изображен график распределения парциальных сил F(x), действующих на дифференциальные объемы движущейся внутри магнитного зазора пара- диамагнитной смеси dv=Sdx со стороны однородного магнитного поля напряженностью H и изменяющих свой знак (направление действия) при координате х=L/2. Интеграл от указанных парциальных сил по всему промежутку магнитного зазора длиной! определяет результирующую силу F_Σ, действующую непрерывно во времени и достигающую максимума при определенной угловой скорости ω* вращения кольца (диска) 1.

Рассмотрим действие заявляемого устройства.

Пусть в прозрачную (например, стеклянную) цилиндрическую колбу 7 с откаченным из нее воздухом помещены кольцо (диск) 1 из пара-диамагнитной смеси с осью вращения 2, опирающейся на элементы крепления 5 и 6 (например, рубиновые камни, как в механических часах). Кольцо (диск) 1 помещено в магнитные зазоры первого 3 и второго 4 постоянных магнитов, закрепленных на стенках цилиндрической колбы 7, например, приклеиванием. На оси вращения 2 закреплен многополюсной ферромагнитный диск 10, магнитно связанный через стенку цилиндрической колбы 7 со съемным устройством 11, создающим вращающееся магнитное поле, электрически подключенным к многофазному генератору переменного тока 13 с регулируемой частотой. Это съемное устройство 11 опирается на подставку 12, высота которой определяет оптимальную магнитную связь съемного устройства 11 с многополюсным ферромагнитным диском 10, используемым для первоначального раскрута оси вращения 2 до некоторой угловой скорости, после чего съемное устройство 11, подставка 12 и многофазный генератор переменного тока 13 удаляются с места установки устройства для демонстрации непрерывного во времени вращения кольца (диска) 1 с некоторой установившейся угловой скоростью вращения без видимого притока энергии извне.

Для снижения потерь на трение в устройстве использован магнитный подвес, выполненный на основе двух намагниченных ферромагнитных тороидов 8 и 9, обращенных друг к другу одноименными магнитными полюсами. Первый намагниченный ферромагнитный тороид 8 закреплен на оси вращения 2 траверсами и вращается вместе с осью вращения 2, а второй намагниченный ферромагнитный тороид установлен на днище прозрачной цилиндрической колбы 7, например, приклеиванием. При этом сила давления оси вращения 2 на нижний элемент крепления 6 существенно снижается. Снижению потерь на трение способствует также откачка воздуха из прозрачной цилиндрической колбы 7 Это обеспечивает непрерывное во времени вращение кольца (диска) 1 с осью вращения 2 и связанными с ней механически первым намагниченным ферромагнитным тороидом 8 и, многополюсным ферромагнитным диском 10 под действием возникающей микросилы F_Σ в кольце (диске) 1, коллинеарной вектору скорости V протяжки пара- диамагнитной смеси внутри магнитного зазора первого 3 и второго 4 постоянных магнитов, создающей вращательный момент, соизмеримый с моментом трения оси вращения 2 в установившемся режиме вращения.

При первоначальной раскрутке оси вращения 2 с кольцом (дискам) 1 и элементами 8 и 10 частота в многофазном генераторе переменного тока 13 должна возрастать от некоторого минимального значения, достаточного для задания вращательного движения многополюсного ферромагнитного диска 10, до некоторого максимального значения, после чего этот генератор отключается.

Рассмотрим теоретические аспекты, объясняющие работу заявляемого устройства.

Намагниченность магнетика J при изменении напряженности Н магнитного поля происходит не мгновенно, а с временным запаздыванием с учетом постоянной т магнитной вязкости по экспоненциальному закону [5-7]:

где ΔJ(t) изменение намагниченности во времени, J_O и J_∞ - соответственно значения намагниченности непосредственно после изменения напряженности Н магнитного поля в момент времени t=0 и после установления нового равновесного состояния. Значение т зависит от природы магнитной вязкости и в различных магнетиках может изменяться в пределах от тысячных долей микросекунды до нескольких десятков часов. Как известно, намагниченность J определяется выражением

где В=µ₀µH - магнитная индукция, µ₀=1,256·10^-6 Гн/м - абсолютная магнитная проницаемость вакуума, µ - относительная магнитная проницаемость магнетика, X - удельная магнитная восприимчивость магнетика, которая равна X=(µ-1) Поскольку, как известно, в парамагнетиках и диамагнетиках значение магнитной восприимчивости практически не изменяется при изменении напряженности H магнитного поля вплоть до его сверхсильных значений, то намагничивание при включении магнитного поля H (из состояния Н=0 в момент времени t=0) намагниченность магнетика в функции времени изменяется согласно (1) и (2) по закону:

Рассмотрим смесь из парамагнетика с магнитной восприимчивостью X₁ и постоянной магнитной вязкости т₁ и диамагнетика с магнитной восприимчивостью X₂ и постоянной магнитной вязкости т₂, причем относительные концентрации x₁ парамагнетика и х₂ диамагнетика при расчете их величин для интервала времени Δt движения любого дифференциального объема Sdx смеси в магнитном поле H, где S - площадь поперечного сечения смеси, ортогонального направлению движения смеси вдоль оси х, a dx - бесконечно малая толщина смеси вдоль оси х, выбираем по условию:

λ

и условие (4) означает, что указанная смесь в магнитном поле H≠0 к концу магнитного зазора постоянного магнита оказывается суммарно размагниченной. Однако в течение времени установления такого процесса размагничивания в смеси, компоненты которой имеют разные постоянные магнитной вязкости т₁ и т₂ намагниченность смеси отлична от нуля; вначале растет, достигая максимума, а затем более медленно уменьшается до нуля при t=Δt.

Таким образом, согласно (3) для компонент однородной смеси можно записать значения намагниченностей в функции времени выражениями:

Кривые намагниченностей компонент пара- и диамагнетиков смеси с учетом их концентраций x₁ и х₂ представлены на рис.2.

При выполнении условий при выборе компонент смеси таким образом, что:

суммарная намагниченность смеси с учетом отрицательного значения магнитной восприимчивости X₂ согласно (5-7) изменяется во времени с учетом концентраций x₁ и х₂ по закону:

Кривая суммарной намагниченности смеси согласно (8) представлена на рис.2. Согласно (8) понятно, что при соблюдении условия (4) при t=Δt суммарная намагниченность смеси отсутствует, то есть J_Σ(Δt)=0, где Δt=L/V, L - длина магнитного зазора постоянного магнита вдоль оси х, V - скорость движения смеси в магнитном поле напряженностью H. Укажем, что это условие размагничивания смеси к концу магнитного зазора L достигается при определенной скорости V=V^* смеси. Если скорость V>V^*, за время прохождения дифференциального объема S dx внутри зазора постоянного магнита смесь размагнититься не успеет. Если V<V^*, то за это же время смесь изменит знак намагничивания и также будет иметь остаточную намагниченность. Априори отметим, что при любых отклонениях скорости движения V смеси в магнитном поле от значения оптимальной скорости V^* значение максимума суммарной намагниченности Max J_Σ(t) будет меньше того максимума суммарной намагниченности, который достигается при V=V^*.

Отрезок времени Δt^*, в течение которого происходит полное (до нуля) размагничивание дифференциального объема S dx смеси на пути L находится из решения уравнения (8) подстановкой в экспоненциальные множители значения Δt^*, что записывается выражением:

Поскольку µ₀ H≠0, то выполнение равенства (9) достигается при условии, что:

Обозначим т₂/т₁=α>1, x₂|X₂|/x₁X₁=β>1. Тогда (10) можно переписать в виде:

и после сокращения обоих частей равенства (11) на x₁X₁>0 получим:

Путем несложных преобразований (12) приходим к трансцендентному уравнению относительно искомой величины Δt^* следующего вида:

в которое следует подставить известную величину α=т₂/т₁ для выбранных парамагнетика и диамагнетика в составе смеси с варьированием величины β=х₂|X₂|/x₁X₁ до тех пор, пока не будет достигаться максимум действующей силы на движущуюся в магнитном поле смесь. Решение этого уравнения целесообразно проводить на персональном компьютере численными методами с использованием программы Mathcad.

Теперь следует обратиться к расчету действующей на смесь силы со стороны магнитного поля в зазоре постоянного магнита длиной L вдоль направления движения смеси (оси x, ортогональной вектору поперечного постоянного магнитного поля с напряженностью H). При выборе зазора с неизменным расстоянием между полюсами постоянного магнита, магнитное поле считается однородным внутри зазора.

Поскольку положение дифференциального объема S dx вдоль оси х в функции времени характеризуется уравнением х=Vt, то уравнение (8) можно переписать в виде:

и значение дифференциального магнитного момента этого объема равно:

Как известно, сила F, действующая на диполь с моментом М в неоднородном магнитном поле с градиентом поля dH/dx, равна F=М grad Н_Х. В рассматриваемой задаче магнитное поле однородное вдоль оси х с напряженностью поля Н=const(x), однако в динамике процесса (при V>0) неоднородной является намагниченность различных по координате x дифференциальных объемов S dx смеси. Поэтому известное выражение для силы в неоднородном магнитном поле можно адекватно заменить на выражение для силы неоднородно намагниченного магнетика (смеси) в однородном магнитном поле. Тогда имеем связь вида

Тогда с учетом (15) и (16) для дифференциала силы F(x), действующей со стороны магнитного поля на дифференциальный объем dv=Sdx, находящийся на координате х, где 0≤х≤L, получим выражение:

В выражении (17) введен множитель [1-(2x/L)], учитывающий влияние центра симметрии магнитного поля, при однородности которого этот центр находится на координате х=L/2, на величину силы, действующей на дифференциальный объем S dx смеси, находящийся внутри зазора постоянного магнита на произвольной координате х, отстоящей в ту или иную сторону от центра симметрии магнитного поля, поскольку в диапазоне координат 0≤х≤L/2 дифференциальный объем смеси притягивается к центру магнитного поля, создавая движущую силу в направлении движения смеси, а в диапазоне L/2≤х≤L, наоборот, дифференциальный объем смеси, также притягиваясь к центру симметрии магнитного поля, создает торможение движущейся смеси, что и учитывается указанным множителем. Так, при положении дифференциального объема S dx смеси на координате х=L/2 сила F(L/2)=0., как это видно на графике рис.4.

Полная действующая на движущуюся смесь сила F_Σ определяется интегрированием парциальных сил F(x) на промежутке 0≤х≤L, при следующей замене переменных интегрирования ε=х/L, β=x₂|X₂|/x₁X₁, α=т₂/т₁, dε=dx/L, Δt=L/V, что отражается следующим выражением:

Выражение µ₀H²Sx₁X₁=D=const, имеющая размерность силы (в ньютонах), 0≤ε≤1.

Функция относительной силы Ф(α, β, Δt, т₁) согласно (18) имеет вид интеграла от безразмерной переменной ε:

Интеграл (19) является суммой четырех интегралов:

Сумма интегралов (20) равна Ф(α, β, Δt, т₁)=I₁+I₂+I₃+I₄.

Максимум функции Ф(α, β, Δt, т₁) по переменной Δt находим приравниванием нулю производной от этой функции по переменной Δt, то есть решением dФ Ф(α, β, Δt, т₁)/d(Δt)=0.

Эта производная может быть взята по частям с последующим суммированием результатов.

Приравнивая сумму производных нулю p₁+p₂+р₃+р₄=0, находим решением полученного трансцендентного уравнения значения Δt^*, при котором обеспечивается максимум действующей силы Max F_Σ

Решением этого уравнения является Δt^*≈т₁(1+eα)/β, где e=2,718 - основание натурального логарифма.

Подставляя в уравнение (13) решение уравнения (22) получим новое уравнение:

которое определяет связь между параметрами α и β^*, обеспечивающую достижение максимума движущей пара-диамагнитную смесь силы. Полагая заданным значение параметра α, находим значение оптимального параметра β^*:

Здесь знак приблизительного равенства предполагает, что величина параметра α существенно больше единицы, и α≥5. Точное решение для α<5 весьма громоздко.

Например, если в качестве парамагнетика выбираем неодим (Nd), для которого значение X₁=490*10^-6, а в качестве диамагнетика выбираем висмут (Bi), для которого |X₂|=16*10^-6, при α=5 для величины параметра β^* получим:

β^*=14,59ехр 0,2/[ехр(-0,8)+5ехр 0,2]=2,718=e.

Поскольку β^*=х₂|Х₂|/x₁X₁=2.718, а |X₂|/X₁=16/490=0,033, получаем соотношение концентраций х₂/х₁/=β^*X₁/|X₂|=2,718/0,033=82,36. Это означает, что в смеси неодима должно быть всего 1,2%, а висмута 98,8%.

Исследуя формулу (24), отмечаем, что значение β^*=2,718 не зависит, в первом приближении, от значения параметра α, но интервал времени Δt^*≈т₁(1+eα)/β^*, полученный из решения трансцендентного уравнения (22), зависит от параметра α, и этот оптимальный интервал времени равен Δt^*≈0,368т₁(1+2,718*α). Так, если α=5, то Δt*=5,37 т₁. Если для неодима постоянная магнитной вязкости составляет величину порядка т₁=5*10^-4 сек, то имеем для Δt^*≈2,685 мс. Это позволяет в рассматриваемом примере определить оптимальную скорость движения смеси в магнитном зазоре с заданной длиной L. Пусть L=2 см=0.02 м, тогда скорость V^*=L/Δt^*=0,02/2,685*10^-3=7,45 м/с. При этом постоянная магнитной вязкости висмута т₂ должна быть равна т₂=αт₁=2,5*10^-3 с. Аналогичным образом можно рассчитать оптимальную скорость протяжки в магнитном поле пара-диамагнитной смеси, при которой достигается максимум движущей силы. Всякое отклонение от этой скорости приводит к снижению движущей силы. Отметим, что точный подбор постоянных магнитной вязкости т₁ и т₂ для конкретно выбранных пара- и диамагнетиков несущественен, если величина α=т₁/т₂≥5. Это условие означает, что установление намагниченности парамагнетика происходит существенно быстрее, чем для диамагнетика, что и позволяет иметь вектор движущей силы в направлении движения смеси в магнитном поле.

Обращаясь к выражению (19) для рассматриваемого примера при подстановке Δt=Δt^*, Δt^*/т₁=5,37, Δt^*/αт₁=1,074 и β=2,718 получим:

Ha основании выражения (18) для рассматриваемого примера находим максимум движущей силы при напряженности магнитного поля в зазоре Н=10⁵ А/м и S=6*10^-5 м²

Полученное значение порядка 8 дин (в системе CGS). конечно, весьма незначительное, чтобы можно было говорить о создании энергетических установок, работающих от тепловой энергии окружающей среды, которая практически даровая и ее «бесконечно» много.

Если пара-диамагнитную смесь выполнить в виде кольца (диска) радиусом R, то при оптимальной скорости движения края кольца (диска), помещенного в магнитный зазор, угловая скорость вращения кольца (диска) должна вычисляться по формуле

и для рассматриваемого примера оптимальная угловая скорость при R=0,1 м и L=0,02 м равна ω*=0,02/0,1*2,685*10^-3=74,5 рад/с, то есть кольцо (диск) должно вращаться с частотой ω^*/2π=11,86 об/сек≈712 об/мин При этом развиваемая движущей силой максимальная мощность равна P^*=ω^*RMaxF_Σ=74,5*0,1*7,75*10^-7=57,74*10^-7 Вт=5,8 мкВт. В принципе этой мощности может оказаться достаточно для вращения динамически сбалансированного кольца (диска) при обеспечении потерь на трение оси вращения, соизмеримых или меньших указанной мощности, например, опорой оси на рубиновые камни, как это используется в часовой промышленности (в механических ручных часах). Такой эксперимент желательно проводить в сосуде с откаченным воздухом, чтобы снизить трение кольца (диска) о воздух.

Отметим, что постоянные магнитной вязкости т₁ и т₂ используемых пара- и диамагнетиков могут быть подобраны введением в смесь дополнительных присадок, влияющих на быстроту разворота магнитных диполей соответствующих веществ в магнитном поле.

Приведем теперь доказательство расходования тепловой энергии внешней среды при реализации магнитокалорического эффекта в магнетиках [8-9].

Пусть в исходном состоянии ненамагниченный магнетик имеет температуру T_O и суммарную удельную теплоемкость c_O. Для рассматриваемой массы магнетика m имеем его внутреннюю тепловую энергию Q_O=c_OmT_O. Если плотность магнетика ρ, то объем указанной массы m равен v=m/ρ. Если указанный объем магнетика поместить в магнитный зазор постоянного магнита, создающего магнитное поле с напряженностью Н, то энергия магнитного поля, запасенная в этом объеме магнетика, как известно, равна W=µ_OµvH²/2, где µ_O=1,256*10^-6 Гн/м - абсолютная магнитная проницаемость, µ - суммарная относительная магнитная проницаемость магнетика (µ≈1). При этом возникает намагничивание магнетика, и закон сохранения энергии выражается соотношением:

где c_H - удельная теплоемкость намагниченного магнетика (c_H<c_O), T₁ - температура объема v магнетика в процессе его адиабатического намагничивания, причем T₁>T_O (при намагничивании, как известно, магнетик нагревается), η - коэффициент магнитокалорической активности магнетика (зависит от компонент смеси). После выхода объема v магнетика из указанного магнитного зазора в процессе его адиабатического размагничивания происходит охлаждение этого объема магнетика, и закон сохранения энергии записывается как:

где Т₂ - температура рассматриваемого объема магнетика при его адиабатическом размагничивании.

Покажем, что Т₂<T_O, то есть внутренняя тепловая энергия данного объема магнетика, который сначала намагничивается в магнитном зазоре, а затем покидает его, размагничиваясь в адиабатическом процессе (за счет вращения магнитного кольца), уменьшается на величину

Согласно (28) можно для значения с_Н записать выражение

Подставляя (31) в (29), получим

Из (32) следует, что

Поскольку ηW/c_Om=µ_OηµvH₂/2c_Om=µ_OηµH²/2ρc_O>0, то действительно имеем неравенство

T_O-Т₂>0, то есть T_O>Т₂,

и конечная температура Т₂ рассматриваемого объема магнетика оказывается ниже его исходной температуры T_O (до входа в магнитный зазор с магнитным полем)

Изменение внутренней тепловой энергии рассматриваемого объема магнетика в процессах его адиабатического намагничивания и размагничивания определено в (30).

Рассматриваемый объем ферромагнетика v=LS, где L - длина магнитного зазора постоянного магнита, S - сечение ферромагнитного кольца, охваченное магнитным зазором с магнитным полем, проходит магнитный зазор за время Δt=L/ωR, где ω - угловая скорость вращения магнитного кольца радиуса R, следовательно, мощность тепловых потерь вычисляется согласно выражению:

Оптимальная угловая скорость ω^* вращения кольца из смеси магнетика, при которой достигается максимум крутящего момента, указана в (27). Подставляя это значение в (34), получим значение максимальной мощности потерь P_MAKC внутренней тепловой энергии данного объема магнетика, равное:

Подставляя в (35), вместо температуры Т₂, ее значение из (33), получим:

где η<1 - так называемый коэффициент магнитокалорической активности, то есть коэффициент преобразования магнитной энергии в понижение температуры магнетика в квазиадиабатическом процессе размагничивания. Следовательно, максимум тепловых потерь в кольце из смеси магнетиков при магнитокалорическом эффекте прямо пропорционален потребленной в магнетике энергии магнитного поля ηW, помещенном в магнитное поле постоянного магнита в его зазоре, и.пропорционален величине e/т₁(1+eα). Безразмерный коэффициент η, в известной мере играет роль коэффициента полезного действия при превращении запасенной в пара-диамегнетике магнитной энергии в механическую.

Адиабатичность процессов намагничивания и размагничивания предполагает практически ничтожное влияние тепловой энергии внешней среды на характер изменения температуры рассматриваемого объема магнетика, хотя это можно считать лишь условно, в первом приближении. После того, как рассматриваемый объем магнетика покидает магнитный зазор постоянного магнита, он достаточно большое время находится вне действия на него магнитного поля. Это время существенно превышает интервал времени Δt, и за это время рассматриваемый объем магнетика за счет притока тепловой энергии из внешней среды вновь нагревается в установившемся режиме до температуры T_O. Это нагревание происходит благодаря тому, что внешняя среда имеет температуру T_CP>T_O, и нагревание рассматриваемого кольца возникает за счет механизма теплопроводности, а в случае вакуумирования вращающегося кольца (диска), как в заявляемом устройстве, за счет пондеромоторного излучения со стенок прозрачной цилиндрической вакуумной колбы 7 (рис.1).

Согласно закону сохранения и превращения энергии тепловая мощность потерь (в оптимальном приближении) Р_МАКС соответствует вращательному моменту М_ВР, возникающему в кольце из смеси магнетиков, равному:

а сила F_Σ, действующая в кольце радиуса R и совпадающая с вектором мгновенной скорости объема магнетика внутри магнитного зазора постоянного магнита, равна:

Если указанный в (37) вращательный момент превышает момент трения и присоединенной нагрузки, то вращение кольца будет продолжаться с непрерывным потреблением тепловой энергии внешней среды, транспортируемой из нее к кольцу через элементы теплопередачи. В противном случае кольцо вращаться не будет.

Сравнивая силу из (26) со значением из (38), получаем связь µ_OηSH²/2=µ₀H²Sx₁X₁ Ф(α, β^*, Δt^*, т₁) и с учетом (25) получим ηµ=0,35x₁X₁, откуда получаем, что минимально возможное значение коэффициента магнитокалорической активности смеси магнетиков η≈0,35x₁X₁. для рассмотренного выше примера (x₁=0,012 и X₁=490*10^-6) получим η≈2,06*10^-6, то есть ничтожная часть энергии магнитного поля используется для осуществления фазового перехода первого рода - уменьшения удельной теплоемкости смеси магнетиков в магнитном поле напряженностью H. При этом не следует считать, что энергия магнитного поля, сосредоточенная в постоянном магните, создающим в его зазоре магнитное поле с напряженностью H, уменьшается в процессе вращения кольца из смеси магнетиков, что подтверждается экспериментами взаимодействия постоянных магнитов с магнитотвердыми ферромагнетиками: их намагничивание магнитом не приводит к снижению намагниченности постоянного магнита. Природа возникновения силы F_Σ в направлении движения смеси магнетиков в зазоре с магнитным полем объясняется уменьшением внутренней (тепловой) энергии этой смеси в присутствии магнитного поля, восполнение которой осуществляется притоком тепловой энергии из внешнего пространства. Уменьшение тепловой энергии смеси магнетиков в квазиадиабатическом процессе размагничивания происходит уже после того, как намагниченная смесь выйдет из магнитного зазора постоянного магнита, то есть является следствием процесса преобразования внутренней энергии смеси магнетиков в механическую в присутствии магнитного поля, являющимся отражением закона сохранения и превращения энергии.

На рис.2 представлены кривые намагниченности J₁(t)*x₁ и J₂(t)*x₂ соответственно парамагнетика и диамагнетика с учетом их концентраций в составе смеси. Видно, что процесс установления намагниченности в парамагнетике происходит в несколько раз быстрее (в α раз), чем процесс намагничивания диамагнетика в смеси, а установившийся режим намагничивания последнего существенно превышает таковой для парамагнетика (в β раз). Однако в течение времени Δt=L/ωR намагниченности парамагнетика и диамагнетика выравниваются J₁(Δt)*x₁=|J₁(Δt)|*x₂, то есть пара-диамагнитная смесь в ее дифференциальном объеме S dx к концу магнитного зазора длиной L полностью размагничивается в суммарном представлении (но не по отдельным компонентам смеси!), то есть J₁(Δt)*x₁-J₂(Δt)*x₂=0.

На рис 2 также представлен график функции J_Σ(t)=J₁(t)*x₁-J₂(t)*x₂ суммарной намагниченности пара- диамагнитной смеси, продвигающейся внутри магнитного зазора постоянного магнита, из которого видно, что по мере продвижения этой смеси внутри зазора намагниченность в соответствующих дифференциальных объемах смеси сначала быстро растет, доходя до максимума, а затем медленно убывает dJ_Σ(t)/dt<0. Это и обеспечивает превышение силы втягивания смеси в магнитный зазор над силами ее торможения, то есть возникновение движущей силы F_Σ>0, совпадающей с вектором скорости дв