Способ автоматического управления двигателями постоянного тока главных приводов прокатного стана

Способ автоматического управления двигателями постоянного тока главных приводов прокатного стана

Иллюстрации

Показать все

Реферат

Изобретение относится к системам автоматического управления двигателями постоянного тока в главных приводах клетей прокатного стана, в задачу которых входит циклическое изменение скорости прокатки и поддержании заданной скорости прокатки при изменении момента прокатки.

Известен алгоритм пропорционально-интегрально-дифференциального (ПИД) регулирования с обратной связью (описанный в Денисенко В.В. «Компьютерное оделирование ехнологическим роцессом, экспериментом, оборудованием»), который доминирует в сфере управления двигателями главных приводов прокатных станов и описывается выражением:

где t - время;

K, T_i, T_d - пропорциональные безразмерные коэффициенты,

y - регулируемая,

u - выходная величина регулятора.

В частном случае пропорциональная, интегральная или дифференциальная компоненты могут отсутствовать и такие упрощенные регуляторы называют П, И или ПИ регуляторами.

Входом объекта управления является выход регулятора, т.е. величина u, которая имеет ту же размерность, что и рассогласование е, выходная величина y и управляющее воздействие r. Т.е., если объект управляется током или частотой вращения вала, во всех этих случаях управляющей величиной является u, а в модель объекта управления Р следует ввести преобразователь величины и в ток или в частоту вращения вала соответственно. Таким воздействием во всех случаях должна быть величина u (выходная величина регулятора). Однако прокатный стан включает в себя линию прокатных клетей, содержащих валковые системы и системы привода, состоящие из шестеренных клетей, редукторов, шпинделей, валов и муфт, что составляет сложную многомассовую систему, не поддающуюся полноценному математическому описанию, кроме того, существует взаимное влияние прокатных клетей друг на друга через прокатываемую заготовку. Сама заготовка имеет неравномерный по длине нагрев и может иметь различные дефекты структуры. Это приводит к непредсказуемым и неравномерным изменениям усилий прокатки, которые через систему привода передаются на вал двигателя. Несмотря на полученные результаты в области создания современной теории оптимальных САУ практическое применение этой теории для синтеза реальных систем пока еще сравнительно ограничено. Это объясняется тем, что построение на основе указанной теории систем для сложных объектов, у которых система описывается дифференциальными уравнениями высокого порядка или имеет сложный характер ограничений, при нынешнем состоянии средств управляющей и вычислительной техники практически не реализуемо. Поэтому существующие САУ используют приближенные алгоритмы управления (квазиоптимальные), незначительно в смысле избранного функционала, отличающиеся от строго оптимальных, но зато просто реализуемые на практике. При этом получается некоторое отклонение процесса от строго оптимального, однако управляющее устройство системы существенно упрощается. Для определения оптимальных коэффициентов существуют известные аналитические методы, такие как, методы Зиглера-Никольса, CHR (Chien, Hrones и Reswick) метод. Расчет параметров по формулам не может дать оптимальной настройки регулятора, поскольку аналитически полученные результаты основываются на сильно упрощенных моделях объекта. В частности, в них не учитывается присутствующая нелинейность. Кроме того, модели используют параметры, идентифицированные с некоторой погрешностью. Поэтому после расчета параметров регулятора производят его подстройку. Подстройку выполняют на основе правил, полученных из опыта, теоретического анализа и численных экспериментов.

Они сводятся к следующему:

- увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости;

- с уменьшением интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее;

- уменьшение постоянной интегрирования уменьшает запас устойчивости;

- увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие.

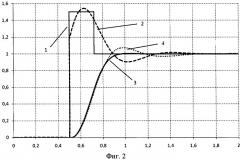
Несмотря на эффективность и широкую распространенность ПИД-регуляторы имеют ряд недостатков. Контуры ПИД-регулирования трудно настраивать, их поведение не всегда предсказуемо, не всегда удается достичь требуемого быстродействия, затруднен поиск неисправностей. Кроме того, поскольку в формировании управляющего сигнала используется значение ошибки в цепи обратной связи форма управляющего сигнала не является идеальной, а «размывается» во времени (линии управляющего (2) и выходного (4) сигналов на фиг.2). Наиболее близким к заявленному изобретению является способ автоматического управления двигателями постоянного тока главных приводов прокатных станов, описанный в SU №1026870 А1, кл. В21В 37/46, 07.07.1983, устройство для управления главным электроприводом клети непрерывного прокатного стана.

Заявлено изобретение, характеризующееся тем, что позволяет решить задачу оптимального управления двигателем постоянного тока, то есть обеспечить выход на заданное значение скорости прокатки за минимальное время при минимальной диаграмме изменения тока якоря, не допуская перегрева двигателя и избежать указанных выше недостатков за счет формирования прямоугольного импульса напряжения в момент возникновения отклонения частоты вращения вала двигателя от заданной. Подобное отклонение возникает в момент изменения заданной частоты вращения, за счет инерционности двигателя и всей системы привода прокатной клети в целом, а так же, в момент изменения усилия прокатки (вход и выход заготовки из клети, неравномерность прогрева заготовки по длине и т.д.).

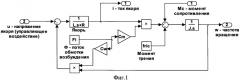
Для определения оптимального управляющего воздействия строится математическая модель двигателя постоянного тока независимого возбуждения, которая описывается следующей системой дифференциальных и алгебраических уравнений:

где u - напряжение на якорной обмотке,

е - ЭДС якоря,

i - ток якоря,

Ф - поток создаваемый обмоткой возбуждения,

М - электромагнитный момент двигателя,

М_с - момент сопротивления движению,

ω - угловая частота вращения вала двигателя,

R - активное сопротивление якорной цепи,

L - индуктивность якорной цепи,

J - момент инерции якоря и привода,

С_ω - коэффициент связи между угловой частотой вращения и ЭДС,

C_M - коэффициент связи между током якоря и электромагнитным моментом.

Для получения передаточных функций к уравнениям применяется преобразование Лапласа при нулевых начальных условиях. Уравнение (2) дает функцию, связывающую ток якоря и падение напряжения на якоре:

Уравнение (3) дает функцию, связывающую динамический момент и угловую частоту вращения:

Схема модели двигателя приведена на фиг.1.

Для формирования оптимального управляющего воздействия составляется таблица зависимости значений выражения от величины и длительности импульса (табл.1). Таблица 1 значений может составляться исходя как из результатов испытаний, так и на базе математической модели привода, при условии ее адекватности реальному приводу. Как известно, для получения оптимального по быстродействию переходного процесса необходимо поддерживать максимальный уровень управляющего воздействия. В данном случае необходимо с максимально допустимым ускорением разогнать систему, а по достижении заданной частоты вращения снизить управляющий сигнал (линии управляющего (1) и выходного (3) сигналов на фиг.2). В идеальном случае при данном подходе можно достигнуть сколь угодно малого времени переходного процесса, однако реальный привод накладывает на способ формирования сигнала следующие ограничения:

- максимально допустимое напряжение, подаваемое на якорь двигателя;

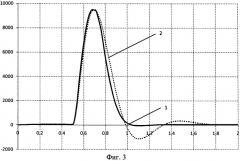
- максимально допустимая перегрузка по току якоря двигателя (линия 1 на фиг.3);

- инерционность многомассовой системы, ограничивающей максимальное ускорение;

- время обработки сигналов существующими АСУ ТП. Предлагаемый способ управления двигателем можно реализовать на

существующих ПИД контроллерах. Для этого полученное значение величины управляющего импульса вводится как коэффициент усиления пропорциональной составляющей, а по истечении необходимого времени регулирования данный коэффициент приравнивается к единице, до возникновения следующего отклонения. Интегральная и дифференциальная составляющие равны 0. На вход регулятора подается заданное значение частоты вращения, а значение отклонения используется для определения времени начала импульса.

Предлагаемый способ позволяет изменять параметры регулирования в широком диапазоне для достижения различных задач (учитывая указанные выше ограничения):

- максимально быстрый выход привода на заданную частоту вращения;

- минимизация токовых нагрузок;

- исключение колебательных процессов перерегулирования;

- оптимизация управления по совокупности времени достижения заданной частоты вращения при минимальном токе якоря.

Таблица значений, графики управляющих и выходных сигналов построены для двигателя МП 7000-115У4 со следующими номинальными параметрами - скорость w=l2.075 с^-1, напряжение u=930 В, ток якоря I=7150 А, максимальная перегрузка по току 2.25 отн.ед., поток обмотки возбуждения Ф=0.4258 Вб, индуктивность якорной цепи L=0.000156 Гн, сопротивление якорной цепи R=0.003682 Ом, совокупный момент инерции многомассовой системы привода J=172000 кгм², коэффициенты C_ω=176 и C_M=172. Параметры импульсного сигнала приняты исходя из равенства максимального тока в якорной цепи при ПИ и предлагаемом регулировании (фиг.3).

Способ автоматического управления двигателями постоянного тока главных приводов прокатных станов, включающий измерение фактической скорости вращения вала двигателя в процессе прокатки, отличающийся тем, что регулируют скорость вращения вала двигателя для поддержания заданной частоты его вращения, при этом замеренную фактическую скорость вращения вала двигателя сравнивают с заданной и при наличии отклонения формируют противоположный по направлению отклонению скорости вращения вала двигателя прямоугольный импульс напряжения, который подают на якорь двигателя, при этом величину и продолжительность импульса напряжения выбирают, исходя из условий обеспечения минимального изменения тока якоря двигателя при максимальной скорости выхода вала двигателя на заданную частоту вращения.