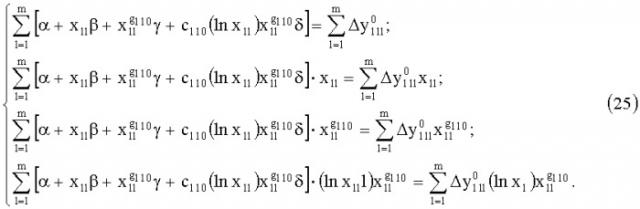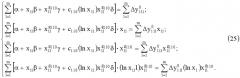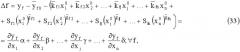Способ измерения полисостава газовых сред

Способ измерения полисостава газовых сред

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к области измерительной техники и может быть использовано для определения полисостава газовых сред, т.е. для определения состава сред, на определенный момент времени включающих ряд газовых компонентов неизвестной концентрации.

Оцениванию состава газовых сред посвящено значительное число работ. В них при выборе метода оценивания концентрации газа обращается внимание на возможность достижения достаточной чувствительности и безопасности [1]. Но в большинстве случаев задача определения газового состава заключается в измерении концентрации какой-либо одной компоненты [2, 3, 4]. Нас, в частности, интересуют способы и средства одномоментного измерения полисостава газовых сред, т.е. измерения концентрации ряда компонент, образующих газовую среду.

Известны способы измерения на основе использования сенсорных матриц и на основе сенсоров с температурным программированием В данном случае мы используем терминологию первоисточников (термин датчик заменяется на термин сенсор).

Матричные системы рассматриваются и анализируются как в зарубежных публикациях [5], так и в отечественных [6]. Приведем краткие выдержки из этих работ, касающиеся предлагаемого изобретения.

Основным подходом к построению этих систем является синтез матриц из сенсоров, каждый из которых имеет более высокую чувствительность к определенному газу, т.е. обладает к нему селективностью. Проградуировав каждый сенсор на концентрацию соответствующего газа, можно получить систему, позволяющую определить состав газовой среды для смеси определенных компонентов. Такая матричная система будет чувствовать столько газов, сколько она имеет сенсорных элементов. В указанных работах отмечается, что получение высокой селективности к заданному газу для каждого элемента - задача не простая с учетом того, что требуется обеспечивать высокую стабильность характеристик каждого элемента (сенсора) в течение всего времени эксплуатации. Поэтому используются методы, связанные с матрицами элементов, различающихся по отдельным свойства или параметрам чувствительного слоя. В этом случае требование высокой селективности элемента к конкретному газу снижается. Подобная матрица имеет набор элементов для достаточно различающихся составов окружающей среды. Это предположение считается оправданным за счет того, что хотя каждый элемент реагирует практически на все газы, его реакция при этом отличается от реакции других элементов. Матрица с большим числом сенсоров позволяет снизить влияние дрейфа характеристик. Его предлагается уменьшать, если учитывать не абсолютные значения характеристик, а характеристики, отнормированные к среднему для всех элементов матрицы. При этом указывается на необходимость установления корреляции между образом на выходе сенсорной системы и составом окружающей атмосферы. Подобные задачи предлагается решать с использованием искусственных нейронных сетей [7] или методами обработки данных на основе анализа главных компонент. Работа [7] также цитируется в [6].

Альтернативой матричным сенсорам выступают сенсоры с температурным программированием [6]. Его суть заключается в циклическом изменении температуры чувствительного слоя сенсора. Это позволяет производить определение состава (разделение состава) газов при помощи одного чувствительного элемента на основе наблюдения его динамических характеристик. Этот принцип разделения состава (селекции) основан на том, что различные газы имеют различные скорости адсорбции, реакции и десорбции на поверхности при различной температуре. Это является причиной того, что при определенной зависимости изменения температуры сенсора, изменение его характеристики (сопротивления) при различных составах окружающей газовой среды будет разным. Особенность описываемого подхода - возможность его вариаций. Меняя закономерность вариаций температуры во времени, можно изменять селективность сенсора к определенному газу.

Как следует из выше изложенного, рассмотренным сенсорным системам должны предписываться, прилагаться соответствующие методы оценивания функции преобразования

где R - отношение, выражающее взаимосвязь вектора входных воздействий и вектора выходных сигналов сенсорной системы;

X - вектор входных воздействий (концентраций исследуемых газов);

Y - вектор выходных сигналов сенсорной системы.

В работе [6] рассматривается тривиальный случай: если «предположить, что зависимость сигнала элемента матрицы от концентрации детектируемого газа линейна, решение задачи можно представить в виде Y=TX, где T - диагональная матрица коэффициентов пропорциональности концентраций и выходных сигналов». И далее констатируется: «…добиться высокой избирательности элементов сенсорной системы сложно, поэтому в реальных случаях элементы матрицы T, не лежащие на главной диагонали, могут принимать ненулевые значения, то есть отдельный сенсор будет реагировать не только на один определенный газ…зависимость выходного сигнала сенсора от концентрации обычно не линейная, и для распознавания состава среды необходимо использовать другие методы».

Для исключения влияния нелинейности предлагается искусственный прием линеаризации системы уравнений (1).

Один из вариантов предлагаемого метода [8] заключается в следующем. Аппроксимируется зависимость выходного сигнала i-го элемента матрицы от состава окружающей атмосферы (функция преобразования i-го элемента) следующим выражением:

где m_ia, m_ib, a _i, b_i, n_i - коэффициенты, характеризующие i-й сенсор, i∈(1, 2, …, N); N - число сенсоров в системе;

A, B, … - концентрации компонентов в распознаваемой среде.

Далее произвольно допускается, что степенные коэффициенты m_ij для каждого газа j для всех сенсоров равны:

m_1a=m_2a=…=m_a,

m_1b=m_2b=…=m_b,

и предлагаются следующие замены:

; ; ; …

С учетом замен получаем линейную систему

Решение системы и обратное преобразование переменных позволяет найти концентрации компонентов окружающей атмосферы.

Но из всех этих рассуждений не ясно, как оцениваются все параметры моделей функций преобразования (2) и как выбираются сами модели указанных функций. На это указывается и в [6]: «К сожалению, выбрать подходящую аналитическую модель очень сложно, к тому же для нее необходимо обеспечить возможность линеаризации».

В работе [8] предлагается еще корреляционный метод. Корреляционный метод разбивается на 2 этапа: 1. Калибровка (градуировка), когда сенсор помещается в среду, содержащую компоненты, на которые необходимо получить желаемый отклик системы; 2. Сенсорная система сравнивает тем или иным способом образы полученной при калибровке выборки, с сигналами, имеющимися на входе в текущий момент времени и решает, к какому классу относится распознаваемый образ - вектор концентраций на входе сенсорной системы.

Предлагаемый корреляционный метод кратко можно представить так. Для заданного диапазона из т концентраций вычисляется величина

где N_ikp - сигнал сенсорного элемента i в присутствии газа k концентрации p.

Нетрудно увидеть, что поученное значение будет являться усредненным откликом i-го элемента на k-й газ заданной рядом концентраций p∈{1, 2, …, m].

Далее оценивается средний отклик всей системы из n сенсоров на идентифицируемый газ:

По аналогии с (4) предлагается оценить S_ijp - отклик элемента i сенсорной матрицы на газ j концентрации и S_jp усредненный отклик всех элементов в тех же условиях:

Корреляционный коэффициент с учетом (4)-(6) записывается следующим образом:

Анализируя этот метод, можно отметить, что усреднение концентрации (4), (5) и откликов элементов (6) заведомо приводит к нивелированию нелинейностей функций преобразования сенсоров, т.е. получаем результат, подобный выше рассмотренному методу линеаризации. Здесь еще добавим, что этот метод обладает низкой чувствительностью, при ρ≤0,7 случайные величины считаются слабо коррелированными [9].

В работе [8] еще предлагается для идентификации концентрации газа использовать векторный метод. Суть его в следующем.

Идентификация газа производится в зависимости от того, попала ли точка, определяемая выходными значениями N сенсоров матрицы, в ту или иную область N-мерного пространства, найденную при калибровке сенсорной системы.

В [6] интерпретируется этот метод следующим алгоритмом нормировки значений выходных сигналов системы. Для сенсоров, построенных на основе полупроводниковых оксидов металлов, функцию преобразования элемента матрицы, которую автор ошибочно называет передаточной, аппроксимируют следующим выражением:

где R_ij - сопротивление i-го элемента сенсорной матрицы в присутствии j -го газа концентрации , a R_i0 - сопротивление i-го элемента в нейтральной среде.

Далее вводится следующее преобразование:

где P_ij подразумевается как вероятность.

Из (9) видно, что P_ij не зависит от концентрации газа.

Переход от (8) к (9) свидетельствует о том, что автор [6] нивелирует нелинейность зависимости R_ij или r_ij от концентрации искусственным приемом, который не приводит к обратному: к значению при дешифровке результатов. Подбор же параметров распределения вероятностей P_ij в пространстве P неизвестно как и по каким правилам, но якобы в соответствии с калибровочными измерениями, имеет много неясностей, и поэтому не имеет утилитарной ценности для приложений в условиях практики.

Известны методы обработки данных на основе использования искусственных нейронных сетей [7]. Их применение предполагается в том случае, если исходная информация нечеткая и представлена функциями принадлежности.

Если эти системы выполнены на основе использования ряда сенсоров и градуируются, использование искусственных нейронных сетей в том плане, что рассматривается в [6, 7], нецелесообразно.

Во всех указанных работах предлагается использовать один канал (датчик, сенсор, фильтр) для оценивания одной компоненты. При этом характеристики каналов так или иначе линеаризируют. Такой подход - достаточно грубое приближение к решению поставленной задачи.

В действительности же каждый канал испытывает воздействие в той или иной степени всех компонентов газовой среды. Поэтому возникла задача разработки нового, более обобщенного способа оценивания компонентов на основе универсальной математической модели многоканальной системы, каждый канал которой имеет наибольшую чувствительность к одной компоненте и менее чувствителен к другим, но влияние которых должно быть учтено в соответствующей математической модели функции преобразования, основные параметры которой должны определяться на основе натурных экспериментов (градуирования системы). Последнее позволит повысить точность оценивания каждой компоненты и одновременно - получить интегральную оценку состава всей газовой среды.

Таким образом, основу предлагаемого способа составляют процедуры градуирования системы и разработка операций формирования ее математической модели и дешифровки выходных сигналов системы. Суть градуирования будет ясна в процессе синтеза математической модели.

Чтобы решить эту задачу, целесообразно привести предварительно качественную оценку соответствия модели натурным данным: данным градуирования отдельных датчиков.

Ее суть в визуальном (качественном) оценивании наличия линейных и нелинейных составляющих в выходных данных (сигналах) датчиков (сенсоров), используемых в системе. В качестве последних широко используются сенсоры (датчики) фирмы Figaro Engineering Inc (Япония) TGS 2600-1; TGS 2602-2; TGS 2611-2; TGS 2612-2; TGS 2620-2; TGS 800-1; TGS 822-1; TGS 823-1. Их выходные сигналы представляются соответствующими графиками значений (вариациями) активных сопротивлений. Из графиков реальных выходных сигналов этих датчиков следует, что наряду с линейными составляющими они содержат весьма значительные и нелинейные составляющие - до 20% и более. Этот факт свидетельствует о том, что каждый датчик должен иметь параметры, учитывающие по масштабу и по форме нелинейность. При этом нелинейность изменяется достаточно существенно при градуировании датчиков (сенсоров) в различных средах: качественно и количественно.

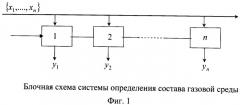
Так как суммарный состав газовой среды содержит n различных составляющих (компонент), каждая из которых одновременно воздействует на каждый канал (датчик, фильтр, сенсор) системы (фиг.1), то их чувствительности должны быть различными к различным компонентам и между собой. Это будет обеспечивать значительную селективность одних датчиков к определенным компонентам (естественным входным величинам) и меньшую селективность к другим, которая будет использоваться для определения поправок, исключающих влияние не естественных входных величин. Это пояснение соответствует первому пункту формулы изобретения. Далее последуют пояснения ко второму пункту формулы изобретения.

Под математической моделью предлагаемого способа оценивания полисостава газовой среды целесообразно понимать функцию преобразования полисостава газовой среды всей системы, предназначенной для реализации способа (не отдельного канала), содержащую при этом линейную и нелинейную части, варьирующую в широком пределе нелинейность.

Общие принципы синтеза подобной модели содержится в [10, 11]. В нашем случае требуется их расширение и доработка.

Пусть имеем {x₁, …, xn} - суммарный состав (полисостав) газовой среды, воздействующей одновременно на все входы системы; y₁ - выходной сигнал с первого канала, y₂ - выходной сигнал со второго канала, y_n - выходной сигнал с n-го канала (фиг.1).

В связи с тем, что исследуемая среда воздействует на все каналы, то их функции преобразования можно записать вначале в упрощенном виде: как систему линейных уравнений

где x_i - неизвестные величины - компоненты (составляющие) полисостава, которые следует измерить (определить), j∈{1, 2, …, n};

y₁, …, y_j, …, y_n - выходные сигналы каналов; j∈{1, 2, …, n};

y₁₀, …y_j0, …, y_n0 - начальные выходные сигналы каналов;

k₁₁, k₁₂, …, k_n - чувствительности первого канала к x₁, …, x_n;

k_n1, k_n2, …, k_nj, …, k_nn - чувствительность n-го канала к х₁, …, x_n;

y_j0, k_ji - определяются в процессе индивидуальных градуировок всех (j) каналов по каждой x_i составляющей полисостава, j∈{1, 2, …, n).

Последнее пояснение раскрывает особенности градуирования системы.

Решение поставленной задачи в виде операции решения линейной системы (10) - весьма тривиально: оно не учитывает нелинейные составляющие выходных сигналов. Поэтому система (10) должна приводиться к нелинейному виду.

Для этого функция преобразования каждого j-го канала представляется по компоненте х₁ так

где - начальные выходные сигналы каждого канала, обусловленные х₁-ой компонентой;

y₁₁, …, y_j1, …, y_n1 - выходные сигналы 1, …, n каналов, обусловленные x₁-ой составляющей;

c₁₁ - коэффициент (масштаба) при нелинейной составляющей, выраженной степенной функцией ;

g₁₁ - показатель степени (формы), соответствующий первому каналу для первой составляющей x₁;

c_n1, g_n1 - аналогичные коэффициент и показатель для n-го канала при x=x₁.

Таким же образом записываются функции преобразования для всех x_i составляющих. Так для x_n получим

Для промежуточных систем вида (12) для x_i, i∈{1, …, n} будет использоваться символика y_1i, …, y_ni.

Теперь, используя (11), (12), система (10) выражается в уточненном виде так

где

В системе (13) неизвестны следующие параметры: , которые определяются через неизвестные , а также неизвестные k_1i; S_1i, …, k_ni; S_ni; g_1i,…, g_ni.

Для нахождения этих параметров необходимо выполнить натурный эксперимент - произвести градуировку системы по каждой составляющей газовой среды по определенной методике.

Отметим особенности методики градуирования системы.

Она будет состоять из n этапов, каждый из которых определяется тем, что подаются на вход системы отдельно х₁, х₂, …, x_n составляющие и снимаются соответственно со всех каналов сигналы y₁; y₂; …; y_n. По этим данным определяются с учетом (12) частные функции преобразования для каждого канала по x₁(х₁∈{х₁₁, х₁₂, …, x_1i, …, x_1m})

где индекс l соответствует l-ому значению х₁, заданному при градуировке (x₁∈{х₁₁, х₁₂, …, x_1l, …, x_1m}), m - соответствует числу точек, взятых по шкале x₁.

При градуировке по другим компонентам х₂, …, x_n действия аналогичны. Так по результатам градуировки по x_n (x_n∈{x_n1, x_n2, …, x_n1, …, x_nm}) имеем аналогичные выражения частных функций преобразования в виде

Здесь индекс n (верхний в ) соответствует x_n.

Каждая функция (15) может быть в общем виде представлена графически (фиг.2). Всего на рисунке n-графиков, соответствующих числу датчиков.

При градуировке по другим компонентам x₂, …, x_n действия аналогичны. Так при градуировке по x_n∈{x_n1, x_n2, …, x_ni, …, x_nm будем иметь аналогичные выражения частных функций преобразования в виде

Теперь, имея значения {х₁₁, х₁₂, …, x_1i, …, x_1m}; …; {x_n1, x_n2, …, x_ni, …, x_nm} и соответствующие значения {y₁₁₁, y₁₁₂, …, y_11i, …, y_11m}; …; {y_nn1, y_nn2, …, y_nni, …, y_nnm}, определяются параметры частных функций преобразования, но для этого потребуется разработка соответствующего аппарата с использованием систем условных уравнений [10] - условных зависимостей.

С учетом всего изложенного модель системы в общем виде определяется как система суммы частных функций преобразований для всех каналов

где j∈{1, 2, …, n};

i∈{1, 2, …, n};

n соответствует числу определяемых (контролируемых) компонент и числу каналов системы.

Таким образом, нами изложена суть нового способа на основе разработанной математической модели многоканальной системы оценивания полисостава газовой среды, которая представляет собой систему взаимосвязанных функций преобразования отдельных каналов по всем компонентам газовой среды, включающих как линейные, так и нелинейные составляющие модели системы.

Далее изложим суть и детали алгоритма оценивания параметров математической модели системы.

В соответствии с известной работой академика А.Н. Колмогорова [12] под алгоритмом в рассматриваемом случае будем понимать совокупность (последовательность) процедур, представленных лингвистически или аналитически: в виде математических выражений. При разработке алгоритма воспользуемся математической моделью системы, рассмотренной выше, и используем при этом операции синтеза и решений системы условных уравнений, предложенных и разработанных авторами [10, 11].

Система условных уравнений для частной функции преобразования (для первого канала) по х₁ (первого уравнения системы (15)) и с учетом определенных конкретных значений параметров ( ; k₁₁=k₁₁₀; c₁₁=c₁₁₀; g₁₁=g₁₁₀) представляется так

которую с учетом модели функции преобразования канала и того, что

следует переписать в виде

где l∈{1, 2, …, m} - порядковый номер замера x₁ - параметра (компоненты);

Индекс (0) означает начальное приближение.

Выражение (20) - линейная неоднородная система с неизвестными α, β, γ, δ. Ее решение - тривиальная задача, но пока для этого не найдены значения y₁₁₀; k₁₁₀; c₁₁₀; и g₁₁₀. Для их нахождения укажем методику.

Можно эвристически (приближенно) оценить g₁₁₀: если графики градуировочных данных, допустим, вогнуты, то g₁₁₀>1 и его можно принять равным любому числу больше 1, например, 1,1. Значения же y₁₁₀; k₁₁₀; c₁₁₀ оценим как решение следующей системы (линейной и неоднородной)

где пусть l∈{1; m/2; m}. Это соответствует методу выбранных точек. Система (21) конкретно представится так

Далее находятся оптимальные значения α, β, γ, δ, соответствующие всем данным натурного эксперимента (градуирования). Для решения этой задачи составляется сумма квадратов

Неизвестные параметры α, β, γ, δ в сумме квадратов (23) должны быть выбраны так, чтобы S₁→min.

Необходимое условие min известно

которое представляется в виде следующей системы

Путь решения системы известен, например, по правилу Крамера или Гаусса. Ее решение находится в виде значений α=α₁; β=β₁;γ=γ₁; δ=δ₁. Тогда уточненные значения (первое уточнение) параметров функции преобразования первого датчика определяются таким образом

Далее процесс итерации продолжается с учетом полученных уточнений параметров выражения (α, β, γ, δ) (20). Для этого выражение (20а) переписывается так

,

а (25) - в виде

Ее решение - числа α=α₂; β=β₂; γ=γ₂; δ=δ₂, которые вторично уточняют значения параметров функции преобразования. При этом получим

Таким образом, указанные операции продолжаются до тех пор, пока не наступят колебания значений каждого параметра относительно некоторых значений. Покажем это на графике, например для k₁₁ (фиг.3).

Из рисунка следует, что после t_1l-шага для k₁₁ наступают колебания относительно некоторого значения.

С учетом этого определяются средние уточненные значения параметров функции преобразования первого канала

Аналогично находятся , , .

Далее изложенные операции необходимо повторить для каждой оставшейся нерассмотренной компоненты x₂, …, x_n. После этого функция преобразования первого канала для совокупности всех компонент газовой среды синтезируется с учетом частных функций преобразования по каждой i-ой компоненте в виде

где ;

i∈{1, 2, …, n}.

Повторяя изложенные операции для всех каналов, получим совокупность их моделей - функций преобразования. Так для канала с номером j выражение (30) по структуре останется таким же, но с измененной символикой, учитывающей конкретный канал

где .

Придавая произвольные значения j∈{1, 2, …, n}, получим любую конкретную функцию преобразования, соответствующую каналу с номером j. С учетом всех уравнений (11): при j∈{1, 2, …, n] получим конкретную модель системы (17).

При этом уточненная функция преобразования каждого канала носит интегральный характер, так как учитывает воздействие на канал всего комплекса компонент газовой среды. Последнее при разработке соответствующих алгоритмов обработки экспериментальных данных (данных градуирования - данных натурного эксперимента) позволяет повысить точность одновременного оценивания полисостава газовой среды.

Разработанный и предложенный авторами алгоритм оценивания параметров многоканальной системы оценивания полисостава газовой среды позволяет свести решение системы нелинейных неоднородных уравнений к решению системы линейных неоднородных уравнений, что значительно облегчает решение поставленной задачи, а также учитывает все имеющиеся экспериментальные (натурные) данные градуирования и позволяет путем последовательных итераций определить указанные параметры с требуемой точностью. Отмеченное выражает достоинства разработанного способа измерения полисостава газовых сред.

Далее дадим пояснения к третьему пункту формулы изобретения.

После того, как получены уточненные, в результате итераций, выражения функций преобразования всех датчиков системы (фиг.1), необходимо разработать алгоритм расшифровки (дешифровки) результатов измерений, т.е. по данным {y_f; x_j}, где y_f - показание f-го датчика, необходимо найти - неизвестные значения концентраций каждой компоненты.

Для решения этой задачи расширим предложенный выше алгоритм. Для этого в системе (31) отбрасывается нелинейная часть и решается линейная система уравнений относительно x₁, x₂, …, x_n. Таким образом получается исходное (нулевое) приближение к начальным значениям

Затем приведем систему к виду

где

Подставляя в систему (33) значения производных (34), посчитанных по данным, полученным на основе результатов первого процесса итераций, и с учетом результатов (32), получим известного вида систему линейную и неоднородную. Ее решение - значения

которые позволяют найти уточненные значения

Теперь, повторяя процесс итерации до колебательного состояния, получим усредненные значения концентраций каждой компоненты

где l для каждой j-ой компоненты может оказаться своим.

Таким образом, нами рассмотрены операции решения прямой задачи: определение параметров функций преобразования по известным входным и выходным сигналам датчиков, и решение обратной задачи: по известным параметрам функций преобразования датчиков и выходным сигналам датчиков определение входных сигналов, поступающих на датчики.

Из всего изложенного следует подтверждение четвертого пункта формулы изобретения: чтобы получить объективную информацию на определенный момент времени, результаты измерений по всем каналам должны быть фиксированы (привязаны) к определенным временным сечениям. Тогда и оценка полисостава будет отвечать соответствующим моментам времени.

При этом дополнительно поясним, что фиксация выходных сигналов датчиков предполагает не регистрацию, в отличие от [13], которая может быть и с различными временными сдвигами и запаздываниями, а точную (с допустимой погрешностью) констатацию соответствия по времени выходных сигналов всех датчиков. Патент [13] п.1 соответствует прототипу предлагаемого способа.

Литература

1. Розанов С.В., Рязанов А.В., Цибизов В.А. Безопасность труда в промышленности. 2002, №1, с.32-34.

2. Агеев В.Н., Бекман И.Н., Бурмистрова О.П. Взаимодействие водорода с металлами. М.: Наука, 1987.

3. Игнатьева И. Датчики газа фирмы Figaro //. Электронные компоненты. 2003, №2, с.99-102.

4. Маринина Л.А. Микроэлектронный чувствительный элемент датчика газообразного водорода. Диссертация на соискание ученой степени кандидата технических наук. Пенза, ПТУ, 2006, 156 с.

5. P. Althainz, J. Goschnic, S. Ehrmann, H.J. Ache, "Multisensor microsystem for contaminants in air", Sensors and Actuators В 33 (1996) 72-76.

6. Бурцев M.C. Исследование динамических характеристик полупроводниковых металлоксидных сенсоров. Магистерская диссертация. М.: Московский энергетический институт (технический университет). 2000, 38 с.

7. D. Vlachos, J. Avaritsiotis, "Fuzzy neural networks for gas sensing", Sensors and Actuators В 33 (1996) 77-82.

8. Muller R., "Multisensor Signal Processing.", "Sensors a Comprehensive Survey", ed. W. Gopel, C.N. Zemel, vol.1 p.314-330

9. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. Л.: Энергоатомиздат, 1985, 247 с.

10. Рыжаков В.В., Рыжаков М.В. Прикладная метрология на основе стохастических представлений. М.: Московский физико-технический институт (государственный университет), 2007, 176 с.

11. Рыжаков В.В., Рыжаков М.В. Разработка и исследование математических основ метода определения состава газовых сред. Научно-технический журнал «Оборонный комплекс - научно-техническому прогрессу России». М.: ВИМИ, 2010, №4, с.93-98.

12. Колмогоров А.Н. К определению алгоритма // Успехи математических наук. Т.XIII, вып.4 (82), 1958 г., с.3-28.

13. Патент номер 2171468. Способ анализа состава газовых смесей и газоанализатор для его реализации. Класс(ы) патента: G01N 27/12, G01N 27/416. Патентообладатель: Сомов С.И.

1. Способ измерения полисостава газовых сред, включающий использование ряда датчиков и их индивидуальное градуирование только по одной газовой компоненте - естественной входной величине, соответствующей назначению датчика, определение функций преобразования и их параметров по данным градуирования, фиксацию и дешифровку выходных сигналов, отличающийся тем, что, с целью повышения точности одновременного измерения концентрации по каждой газовой компоненте (полисостава газовой среды), в измерительную систему для измерения полисостава газовой среды включаются датчики с различными чувствительностями между собой по различным компонентам, каждый из которых одновременно со всеми индивидуально градуируется по всем компонентам измеряемого полисостава газовой среды.

2. Способ по п.1, отличающийся тем, что вводится операция формирования в общем виде функции преобразования полисостава газовой среды каждого датчика и вводятся операции определения параметров уточненных функций преобразования всех датчиков системы по данным индивидуального градуирования каждого датчика системы по всем компонентам измеряемого полисостава газовой среды на основе использования условных зависимостей данных градуирования.

3. Способ по п.1, отличающийся тем, что вводится операция дешифровки выходных сигналов датчиков на основе одновременного системного использования уточненных функций преобразования всех датчиков и всех их выходных сигналов, отражающих воздействие газовой среды неизвестного полисостава.

4. Способ по п.1, отличающийся тем, что в процессе измерения полисостава газовой среды выходные сигналы всех датчиков фиксируются одновременно с привязкой к одной временной шкале (с одним началом отсчета времени) или с последующей коррекцией времени снятия показаний с учетом запаздывания фиксации показаний каждого датчика.