Способ определения локального изменения концентрации примеси в потоке жидкости

Способ определения локального изменения концентрации примеси в потоке жидкости

Иллюстрации

Показать все

Реферат

Изобретение относится к методам измерения и может быть использовано для оценки нестационарной концентрации примеси в определенной точке течения.

Известно, что наличие примеси изменяет различные свойства несущей жидкости, такие как плотность, цвет, радиоактивность, магнитные и тепловые свойства, а также удельное электрическое сопротивление. Таким образом, по измерениям физических свойств возможно оценить концентрацию примеси, в частности, состав солевого раствора, водонефтяной эмульсии и других смесей можно установить при измерении электрического сопротивления. Из уровня техники известны способы определения концентрации: визуальный по цвету примеси, косвенный по электропроводности потока и т.д. (см., например, М.Levy, В.Berkowitz, Measurement and analysis of non-Fickian dispersion in heterogeneous porous media. Journal of Contaminant Hydrology // 2003, 64, pp.203- 226; Gas В, Zuska J, Coufal P, van de Goor T. Optimization of the high-frequency contactless conductivity detector for capillary electrophoresis, Electrophoresis // 2002, v.23, pp.3520-3527).

Основной проблемой в известных способах является усредненный характер измерений, т.е. существенный временной интервал, обусловленный размерами измерительной ячейки, в течение которого концентрация примеси может существенно поменяться. Предлагаемый способ обеспечивает повышение точности определения концентрации примеси без изменений конфигурации измерительной ячейки.

В соответствии с предлагаемым способом определения локального изменения концентрации примеси в потоке жидкости через измерительную ячейку прокачивают жидкость, содержащую примесь, изменение концентрации которой во времени на входе в измерительную ячейку известно. Определяют изменение концентрации примеси во времени внутри измерительной ячейки и восстанавливают импульсный отклик измерительной ячейки методом деконволюции. Далее прокачивают через измерительную ячейку исследуемую жидкость и определяют изменение концентрации примеси во времени в потоке исследуемой жидкости внутри измерительной ячейки. Изменение концентрации примеси во времени в потоке исследуемой жидкости на входе в ячейку определяют из уравнения

где τ - переменная интегрирования, t - время, I(t) - изменение концентрации примеси в потоке исследуемой жидкости на входе в ячейку, R_σ(t) - изменение концентрации примеси в потоке исследуемой жидкости внутри измерительной ячейки, K(t) - импульсный отклик измерительной ячейки.

Предварительно может быть устанавлена зависимость физического свойства жидкости от концентрации примеси, в этом случае изменение концентрации примеси в потоке жидкости внутри измерительной ячейки определяют путем осуществления измерений физического свойства жидкости.

Измеряемым физическим свойством жидкости может быть электрическое сопротивление, плотность, радиоактивность и т.д.

Дополнительно может быть оценено качество измерительной ячейки, для чего вычисляют разность между концентрацией, измеренной внутри измерительной ячейки, и концентрацией на входе в измерительную ячейку, и по полученной разнице судят о качестве измерительно ячейки.

Качество измерительной ячейки может быть оценено также путем определения импульсного отклика измерительной ячейки с помощью преобразования Фурье и сравнения преобразования Фурье от функции K(t) с константой .

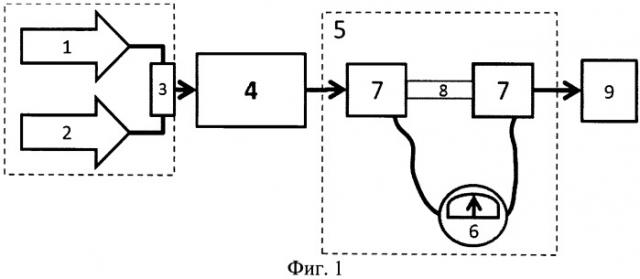
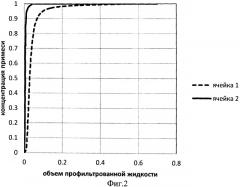
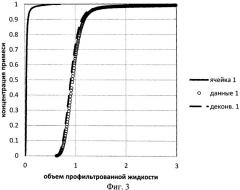
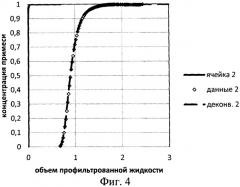
Изобретение поясняется чертежами, где на фиг.1 показана примерная схема экспериментальной установки с измерительной ячейкой; на фиг.2 - результаты измерения концентрации примеси в жидкости для двух измерительных ячеек; на фиг.3 - результаты измерения концентрации примеси в жидкости в первой ячейке и результаты определения концентрации на входе в измерительную ячейку предлагаемым методом; на фиг.4 - результаты измерения концентрации примеси в жидкости во второй измерительной ячейке и результаты определения истинной концентрации предлагаемым методом; на фиг.5 - результаты определения истинной концентрации предлагаемым методом для двух ячеек.

В качестве примера приведен пример реализации изобретения путем измерения такого физического свойства, как электрическое сопротивление жидкости. В этом случае используют измерительную ячейку, состоящую из трубки, выполненной из диэлектрического материала, и двух электродов, контактирующих с жидкостью (Фиг.1). Подобная конструкция ячейки применяется в ряде измерений (см., например, Zhiyao Huang, Jun Long, Wenbo Xu, Haifeng Ji, Baoliang Wang, Haiqing Li. Design of capacitively coupled contactless conductivity detection sensor // 2012, Flow Measurement and Instrumentation, in press). Электрическое сопротивление жидкости внутри трубки связано с концентрацией примеси в потоке. Таким образом, по измерениям сопротивления можно определить концентрацию примеси в объеме, ограниченном трубкой и электродами. Концентрация примеси на входе в ячейку (истинная концентрация) может существенно отличаться от показаний ячейки, измеряющей концентрацию в объеме, ввиду неоднородности поля концентрации. При использовании подобной ячейки необходимо сократить различие между показаниями ячейки и истинной концентрацией примеси на входе в ячейку.

Измерительная ячейка представляет собой систему обработки сигнала. Можно предположить, что эта система обработки обладает свойством линейности и не зависит от времени (Линейная Независимая от Времени Система, далее ЛНВС, для примеров таких систем см., например, J.P.Hespanha, Linear Systems Theory // 2009, Princeton University Press, 263 p., ISBN 978-0-691-14021-6). Если известна импульсная переходная функция ЛНВС, то для любого измеренного выходящего сигнала ЛНВС (отклика на входящий сигнал) можно восстановить этот входящий сигнал методом деконволюции. В свою очередь, импульсную переходную функцию ЛНВС также можно рассчитать методом деконволюции, измеряя отклик ЛНВС на заранее известный входной сигнал.

Входящий сигнал этой ЛНВС - это концентрация примеси в несущей жидкости на входном отверстии в ячейку, выходящий сигнал - это концентрация примеси, расчитанная по измеренному сопротивлению несущей жидкости. ЛНВС характеризуется импульсной переходной функцией, которую также часто называют импульсным откликом системы.

Изобретение позволяет измерять изменение концентрации примеси в несущей жидкости на входе в измерительную ячейку. Процедура измерения проходит в несколько этапов. Предварительно устанавливают зависимость электрического сопротивления исследуемой жидкости от концентрации примеси. Через ячейку прокачивают жидкость, для которой известно изменение во времени концентрации примеси на входе в ячейку, и регистрируют выходной сигнал системы (т.е. измерительной ячейки). Находят импульсную переходную функцию этой системы, применяя, в общем случае, метод деконволюции. Затем регистрируют выходной сигнал системы (т.е. сопротивление) для нового, исследуемого течения с неизвестным изменением концентрации примеси на входе. Наконец, вычисляют неизвестное изменение концентрации примеси на входе в ячейку при помощи метода деконволюции с использованием импульсной переходной функции, найденной ранее, и концентрации в ячейке, известной по измерениям сопротивления.

Для реализации изобретения была использована экспериментальная установка для воспроизведения течения с примесью, показанная на фиг.1. Установка содержит насосную систему 1 для жидкости с известным изменением концентрации на входе в измерительную ячейку, насосную систему 2 для исследуемой жидкости, концентрацию которой нужно определить, кран трехходовой 3; пористую среду 4, измерительную ячейку 5, омметр 6, электроды 7, трубку 8 из диэлектрического материала и систему противодавления 9.

Поле концентрации примеси зависит от времени. Изучая изменение концентрации в определенной точке потока, можно оценить дисперсию примеси внутри пористого образца. Концентрацию примеси возможно определить по изменению удельного электрического сопротивления жидкости внутри измерительной ячейки. Измерения концентрации происходят с ошибкой σ.

Предварительно устанавливают эмпирическую зависимость сопротивления от концентрации примеси (например, от солености жидкости). Эту зависимость используют для оценки концентрации примеси, например, по показаниям омметра для определения концентрации электропроводящей примеси (Фиг.1).

Затем запускают на установке течение, для которого известна динамика распространения примеси, в том числе известно изменение концентрации примеси на входе в измерительную ячейку, равное i(t), где t - время. При этом ячейка регистристрирует изменение сопротивления r_σ(t). Таким образом, обе функции i(t) и r_σ(t) известны.

По данным проведенного эксперимента восстанавливают импульсный отклик системы K(t) (импульсную переходную функцию ЛНВС):

Если в известном режиме течения i(t) ≈1, то ядро легко вычислить по результату измерений как . В противном случае для восстанавления ядра K(t) необходимо использовать деконволюцию, т.е. решить интегральное уравнение в предположении гладкости искомой функции.

Затем проводят эксперимент, в котором необходимо изучить распростанение примеси в потоке. Изменение концентрации примеси на входе в измерительную ячейку - I(t), а изменение концентрации, зарегистрированное в измерениях - R(t). Функция I(t) не известна.

Необходимо найти входящий сигнал I(t), при этом известны переходная импульсная функция K(t) и выходящий сигнал R(t) в виде измеренной концентрации (см. ниже уравнение (2)). Решением задачи является функция I(t), которая оценивает локальное изменение концентрации примеси в потоке.

Разность между входящим и выходящим сигналом может служить оценкой качества измерительной ячейки. При наличии набора измерений {Iⁿ(t), Rⁿ(t)} можно вычислить разность Rⁿ(t)-Iⁿ(t) для интересующих нас течений (n - номер эксперимента). Это позволяет оценить качество измерительной ячейки. Чем меньше данная разность, тем лучше качество измерительной ячейки.

Качество измерительной ячейки можно также оценить после восстановления импульсного отклика. Наилучшее качество измерений соответствует случаю, когда R_σ(t)=I(t). Используя уравнение (2), мы получаем K(t)=δ(t), где δ(t) - функция Дирака. Известно, что преобразование Фурье для функции Дирака . Таким образом, чем ближе преобразование Фурье от функции K(t) к константе , тем выше качество измерений. Расстояние между функциями можно оценивать, например, по L²-норме:

Предложенная процедура была применена при исследовании заводнения керна солевым раствором переменной концентрации. В качестве базовой жидкости использовался раствор NaCl с содержанием 40 г/л, примесь моделировалась раствором NaCl с содержанием 60 г/л. Образец керна (образец пористой горной породы) был помещен в герметичный кернодержатель. Измерительная ячейка располагалась в схеме течения последовательно за кернодержателем и регистировала концентрацию примеси в потоке за кернодержателем.

Первая измерительная ячейка (ячейка 1) состояла из пластиковой трубки со стальными электродами на концах (Фиг.1). Известный режим течения представлял собой распространение примеси в измерительной ячейке в отсутствие керна в схеме течения. Концентрация на входе в измерительную ячейку менялась скачком с 0 до 1, поэтому входящий сигнал является функцией Хевисайда. Зарегистрированный в измерительной ячейке сигнал является результатом сглаживания входящего сигнала. Первая ячейка обладает временем релаксации, за которое ее показания менялись от 0 до 1 при скачке концентрации на входе. Масштабом времени служило время прокачки одного порового объема керна, при темпе закачки 2 см³/мин масштаб времени равен 5 с (Фиг.2, ячейка 1).

Наличие пористой среды (керна) в эксперименте способствует размытию фронта с плавным повышением концентрации на выходе из кернодержателя. Концентрация на входе в ячейку была оценена с помощью предлагаемого метода (Фиг.3, ячейка 1). Она существенно отличалась от измеренной концентрации (абсолютная ошибка между фактической концентрацией на входе в ячейку и измеренной концентрацией достигала 10%).

Была проведена проверка предлагаемого способа путем сравнения результатов для двух разных измерительных ячеек. Эксперимент по заводнению керна был повторен с улучшенной измерительной ячейкой, в которой пластиковая трубка была заменена на стеклянную с меньшим объемом (Фиг.4, Фиг.5, ячейка 2). Улучшенная ячейка обладала меньшим временем релаксации, чем первая ячейка (Фиг.2, ячейка 2). Способ был применен к концентрациям, зарегистрированным двумя разными ячейками, для оценки концентрации примеси на входе в измерительную ячейку. Восстановленные истинные концентрации примеси на входе в измерительную ячейку отличались менее чем на 3% на протяжении всего эксперимента. Проведенное исследование с применением изобретения показало, что усовершенствованная ячейка повысила качество измерений и обеспечила необходимую точность для исследования заводнения керна.

Разность между входящим и выходящим сигналом может служить оценкой качества измерительной ячейки. Входящий сигнал восстанавливается предложенным методом с помощью деконволюции. Разность между сигналами можно считать различными нормами функционалов, например нормой L², равной интегралу квадрата разностей сигналов по временному интервалу. Минимальное значение разности соответствует наиболее точному измерению. Таким образом, при обработке серии экспериментов с помощью деконволюции мы можем судить о качестве измерительной ячейки.

1. Способ определения локального изменения концентрации примеси в потоке жидкости, в соответствии с которым через измерительную ячейку прокачивают жидкость, содержащую примесь, изменение концентрации которой во времени на входе в измерительную ячейку известно, и определяют изменение концентрации примеси во времени внутри измерительной ячейки, восстанавливают импульсный отклик измерительной ячейки методом деконволюции, после чего прокачивают через измерительную ячейку исследуемую жидкость и определяют изменение концентрации примеси во времени в потоке исследуемой жидкости внутри измерительной ячейки, а изменение концентрации примеси во времени в потоке исследуемой жидкости на входе в измерительную ячейку определяют из уравнения где τ - переменная интегрирования, t - время, I(t) - изменение концентрации примеси в потоке исследуемой жидкости на входе в ячейку, R_σ(t) - изменение концентрации примеси в потоке исследуемой жидкости внутри измерительной ячейки, K(t) - импульсный отклик измерительной ячейки.

2. Способ по п.1, в соответствии с которым предварительно устанавливают зависимость физического свойства жидкости от концентрации примеси, и изменение концентрации примеси в потоке жидкости внутри измерительной ячейки определяют путем осуществления измерений физического свойства жидкости.

3. Способ по п.2, в соответствии с которым измеряемым физическим свойством жидкости является электрическое сопротивление.

4. Способ по п.2, в соответствии с которым измеряемым физическим свойством жидкости является плотность.

5. Способ по п.2, в соответствии с которым измеряемым физическим свойством жидкости является радиоактивность.

6. Способ по п.1, в соответствии с которым дополнительно оценивают качество измерительной ячейки.

7. Способ по п.6, в соответствии с которым вычисляют разность между концентрацией примеси в исследуемой жидкости, измеренной внутри измерительной ячейки, и концентрацией примеси в исследуемой жидкости на входе в ячейку, и по полученной разнице судят о качестве измерительной ячейки.

8. Способ по п.6, в соответствии с которым определяют импульсный отклик измерительной ячейки с помощью преобразования Фурье и сравнивают преобразование Фурье от функции K(t) с константой .