Способ определения амплитуды нановибраций по сигналу лазерного автодина

Способ определения амплитуды нановибраций по сигналу лазерного автодина

Иллюстрации

Показать все

Реферат

Изобретение относится к области контрольно-измерительной техники, может быть использовано для определения амплитуд вибраций объектов в десятки нанометров и может найти широкое применение в точном машиностроении и электронной технике.

Известен способ измерения амплитуд вибраций, сущностью которого является получение поля интерференции опорного и измерительного пучков когерентного излучения. Способ заключается в том, что после получения поля интерференции смещают частоту излучения одного из пучков относительно другого на величину, меньшую ω/2, где ω - частота вибрации контролируемого объекта, получают сигнал, пропорциональный яркости поля интерференции, производят фильтрацию сигнала и по его характеру судят об амплитуде вибрации. При фильтрации сигнала в нем оставляют гармонические составляющие с частотами, входящими в интервал nω±Δ, где n=1, 2, 3, …, а Δ<ω, измеряют размах сигнала до и после фильтрации и определяют по формуле амплитуду вибрации (см. патент на изобретение №2217707, МПК G01H 9/00).

Недостатком известного способа является сложная техническая реализация, необходимость измерения яркости полей интерференции, необходимость изменять частоту излучения одного из световых пучков и контролировать ее.

Также известен способ определения амплитуды колебаний объекта по соотношению четных или нечетных гармоник спектрального ряда автодинного сигнала (Усанов Д.А., Скрипаль Ал.В., Скрипаль Ан.В. Физика полупроводниковых радиочастотных и оптических автодинов. Издательство Саратовского университета, Саратов, 2003 г., 312 с.).

Однако данный способ не учитывает влияние внешней оптической обратной связи и не применим для случаев, когда в спектре автодинного сигнала четко различимы лишь две гармоники.

Наиболее близким является способ определения амплитуды вибрации по двум гармоникам спектра автодинного сигнала (патент РФ на изобретение №2300085). Способ заключается в облучении лазерным излучением объекта, преобразовании отраженного от него излучения в электрический сигнал, разложении сигнала в спектральный ряд и измерении амплитуды выбранных гармоник, в спектральном ряде выбирают две соседние гармоники, амплитуду вибрации объекта определяют из соотношения:

с n 2 4 J n 2 ( 4 π λ ξ ) + с n + 1 2 4 J n + 1 2 ( 4 π λ ξ ) = 1

где ξ - амплитуда вибраций объекта, λ - длина волны лазерного излучения, n - целое число, J_n - функция Бесселя n-го порядка, с_n - спектральная составляющая ряда Фурье на частоте n·ν, ν - частота вибраций объекта. (Патент на изобретение РФ №2300085. Способ определения амплитуды вибрации по двум гармоникам спектра автодинного сигнала / Усанов Д.А., Скрипаль А.В., Камышанский А.С. Опубл. 27.05.2007. Бюл. №15. Заявка №2005134749 от 9 ноября 2005 г. Патентообладатель - СГУ.)

Недостатком данного способа является отсутствие возможности учета влияния уровня внешней оптической обратной связи на точность измерений и связанная с этим высокая погрешность измерений.

Задача настоящего способа заключается в определения амплитуды нановибраций по сигналу лазерного автодина с учетом уровня внешней оптической обратной связи для повышения точности измерений.

Технический результат заключается в значительном повышении точности измерения амплитуд нановибраций.

Поставленная задача решается за счет того, что освещают объект лазерным излучением, преобразуют отраженное от него излучение в электрический (автодинный) сигнал, раскладывают сигнал в спектральный ряд и измеряют значение амплитуды гармоники S_x на частоте колебания объекта Ω, отличие предлагаемого способа состоит в том, что на объект накладывают дополнительные механические колебания на частоте Ω₁, измеряют максимальное значение гармоники S_1max, на частоте Ω₁ при изменении амплитуды дополнительных механических колебаний, увеличивают амплитуду дополнительных механических колебаний до появления на автодинном сигнале интерференционных максимумов и минимумов на выделенном участке времени между точками, соответствующими крайним положениям смещения объекта, вычисляют отношение времени убывания t_dec автодинного сигнала ко времени его нарастания t_inc на выделенном участке времени, при этом, если значение t_dec/t_inc больше 1, то вычисляют t_inc/t_dec, по зависимости t_dec/t_inc(C) или t_inc/t_dec(C) определяют уровень внешней оптической обратной связи С, вычисляют S_x/S_1max, по зависимости S₁/S_1max(ξ, C) при определенном ранее С находят амплитуду нановибраций ξ.

Изобретение поясняется чертежами.

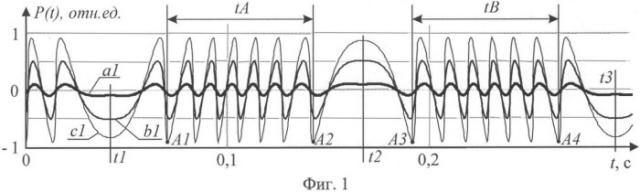
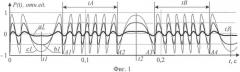
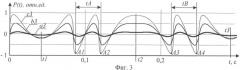
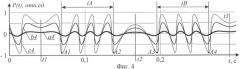
На фиг.1, 2, 3 и 4 представлены переменные составляющие автодинного сигнала для амплитуд вибраций объекта ξ1250 им, 125 нм, 400 нм и 650 нм соответственно. Кривые а1, а2, a3 и а4, представленные на фиг.1, 2, 3 и 4 соответственно, построены при уровне обратной связи С=0, 1; кривые b1, b2, b3 и b4-С=0,5; кривые с1, с2, с3 и с4-С=0,9. На фиг.5 представлена зависимость отношения времени убывания ко времени нарастания функции автодинного сигнала от уровня обратной связи С. На фиг.6, 7 и 8 представлены изображения изолиний амплитуды гармоники спектра автодинного сигнала S₁(ξ,θ) на частоте колебаний объекта при уровнях внешней оптической обратной связи С=0,0001, С=0,5, С=0,9 соответственно. На фиг.9 представлены сечения А, В и С контурных графиков, представленных на фиг.6, 7 и 8 соответственно. На фиг.10 представлены зависимости амплитуды первой гармоники S₁ спектра автодинного сигнала, нормированной на ее максимальное значение S_1max, от амплитуды нановибраций объекта при разных уровнях внешней оптической обратной связи: а10-С=0,0001, b10-С=0,5, с10-С=0,9. На фиг.11 представлена схема экспериментальной установки: 1 - полупроводниковый лазер, запитываемый от источника тока 2, 3 - отражатель, закрепленный на пьезокерамике 4, 5 - генератор звуковых колебаний, 6 - фотодетектор, 7 - фильтр переменного сигнала, 8 - усилитель, 9 - аналого-цифровой преобразователь, 10 - компьютер. На фиг.12 представлен измеренный автодинный сигнал вибраций объекта с амплитудой вибраций, соответствующей максимальному значению первой гармоники его спектра, представленного на фиг.13. На фиг.14 представлен измеренный автодинный сигнал при микровибрациях объекта для определения уровня обратной связи. На фиг.15 представлен измеренный автодинный сигнал вибраций объекта с неизвестной нанометровой амплитудой, на фиг.16 - его спектр. На фиг.17 представлена зависимость амплитуды первой гармоники S₁ спектра автодинного сигнала, нормированной на ее максимальное значение S_1max от амплитуды вибрации ξ, при уровнях обратной связи С=0,19 - кривая а17 и С=0.0001 - кривая b17.

Теоретическое обоснование способа.

Для определения амплитуды вибраций объекта с учетом уровня внешней оптической обратной связи используют следующие теоретические предпосылки.

Переменная нормированная составляющая автодинного сигнала с учетом уровня обратной связи записывается в виде (Усанов Д.А., Скрипаль Ал.В., Скрипаль Ан.В. Физика полупроводниковых радиочастотных и оптических автодинов - Саратов: Изд-во Сарат. ун-та, 2003. 312 с)

P ( t ) = cos ( ω ( t ) ⋅ τ ( t ) ) ,                                       ( 1 )

где ω(t) - частота излучения полупроводникового лазерного автодина, которая находится из фазового уравнения

ω 0 τ = ω τ + C ⋅ sin ( ω τ + ψ ) ,                                           ( 2 )

C = τ ⋅ z ⋅ 1 + α 2 ,                                       ( 3 )

С - коэффициент, характеризующий уровень внешней оптической обратной связи, ω₀=2πс/λ₀, λ₀ - длина волны излучения лазера без обратной связи, с - скорость света, Ψ=arctg(α), α - коэффициент уширения линии генерации, z - коэффициент обратной связи.

При движении объекта по гармоническому закону время обхода лазерным излучением внешнего резонатора изменяется по закону

где Ω - частота гармонических колебаний объекта, τ₀=2L/c, τ_a=2ξ/с, ξ - амплитуда вибраций объекта, ε - начальная фаза колебаний объекта. Численное решение трансцендентного уравнения (2) с учетом соотношения (3) позволяет получить зависимость ω(t) для различных уровней обратной связи С.

Результаты численного моделирования автодинного сигнала P(t), нормированного на амплитуду автодинного сигнала при С=1, для разных уровней обратной связи приведены на фиг.1. При этом в расчетах использовались следующие параметры: ξ=1250 нм, L=8,5 см, ε=π/6, Ω=4 Гц, α=5, λ₀=654 нм.

Из результатов моделирования, приведенных на фиг.1, следует, что с изменением уровня обратной связи изменяются амплитуда и форма автодинного сигнала. С ростом уровня обратной связи увеличивается амплитуда автодинного сигнала P и наблюдается появление участков с несимметричным относительно экстремальных значений P наклоном при движении отражателя. Этот наклон можно охарактеризовать либо величиной отношения времени убывания t_dec автодинного сигнала P ко времени его нарастания t_inc на участке tA между точками А1 и А2, соответствующими первым интерференционным минимумам (максимумам) относительно крайних положений смещения объекта, либо величиной отношения времени нарастания t_inc ко времени его убывания t_dec на участке tB между точками A3 и А4, соответствующими первым интерференционным минимумам относительно крайних положений смещения объекта (фиг.1). На фиг.1 моменты времени t1, t2 и t3 соответствуют крайним положениям смещения объекта при вибрациях. Интерференционные минимумы А1, A3 являются первыми справа относительно крайних положений смещения объекта t1 и t2 соответственно, интерференционные минимумы А2 А4 являются первыми слева относительно крайних положений смещения объекта t2 и t3 соответственно. Следует отметить, что при малых амплитудах нановибраций участки времени tA и tB с интерференционными минимума на автодинном сигнале отсутствуют (фиг.2). Появление данных участков наблюдается при увеличении амплитуд вибраций (фиг.3, 4). Зависимость отношения t_dec к t_inc при выборе участка tA с характерным наклоном вправо от С и зависимость отношения t_inc к t_dec при выборе участка tB с характерным наклоном влево от С совпадают. Данные зависимости приведены на фиг.5.

Теоретический анализ показал, что отношение времени убывания амплитуды автодинного сигнала ко времени ее нарастания не зависит от параметров движения объекта и параметров автодинной системы, а определяется только уровнем внешней оптической обратной связи. Следовательно, отношение времени убывания ко времени нарастания функции автодинного сигнала на заданном временном участке однозначно определяет уровень внешней оптической обратной связи. Кривая, представленная на фиг.5, является зависимостью, по которой можно определить уровень внешней оптической обратной связи.

Для анализа автодинного сигнала удобно применять спектральные методы, в которых для определения амплитуды вибраций используется найденное в результате измерений отношение величин спектральных составляющих или их количество (Усанов Д.А., Скрипаль Ал.В., Скрипаль Ан. В. Физика полупроводниковых радиочастотных и оптических автодинов - Саратов: Изд-во Сарат. ун-та, 2003. 312 с; Pernick В.J. Self-Consistent and Direct Reading Laser Homodyne Measurement Technique Appl. Opt, 12, 607-610 (1973)).

Для описания спектра автодинного сигнала нормированная мощность излучения полупроводникового лазера P(t) может быть представлена в виде разложения в ряд Фурье

P ( t ) = 1 2 a 0 + ∑ n = 1 ∞ { a n cos n ω t − b n sin n ω t } .                       ( 5 )

Первое слагаемое в (5) представляет собой постоянную составляющую автодинного сигнала. Амплитуды спектральных составляющих высших порядков определяются амплитудой колебания объекта.

Ранее было показано (Усанов Д.А., Скрипаль А.В., Авдеев К.С. Изменение спектра сигнала лазерного полупроводникового автодина при фокусировке излучения // Известия высших учебных заведений. Прикладная нелинейная динамика. 2009. Том 17. №2. С.54-65.), что амплитуды спектральных составляющих зависят от амплитуды вибраций ξ и уровня внешней оптической обратной связи С. Для определения амплитуды нановибраций используется амплитуда спектральной составляющей автодинного сигнала на частоте колебаний объекта, значение которой также зависит от стационарного набега фазы излучения лазерного диода θ. Графики зависимости амплитуды спектральной составляющей автодинного сигнала на частоте колебаний объекта от ξ, θ и С приведены на фиг.6, 7 и 8.

На графиках, представленных на фиг.6, 7 и 8, наименьшему значению амплитуды первой гармоники спектра автодинного сигнала соответствует темная область графика, максимальному значению (точки Ма1, Mb1, Ма2, Мb2, Мa3, Мb3) - светлая область графика. На фиг.9 приведены сечения А, В и С графиков, представленных фиг.6, 7 и 8 соответственно, соответствующие максимальному значению амплитуды первой гармоники спектра автодинного сигнала в точке Ма1, Ма2 и Ма3.

Как следует из результатов, приведенных на фиг.6, 7, 8 и 9, при увеличении уровня обратной связи максимальному значению амплитуды первой гармоники соответствуют следующие значения амплитуды вибраций: для точки Ма1 при С=0,0001 ξ_Ma1=96 нм, что соответствует сечению А на фиг.6 и 9, при С=0,5 ξ_Mа2=69 нм, что соответствует сечению В на фиг.7 и 9, при С=0,9 ξ_Ma3=45 нм, что соответствует сечению С на фиг.8 и 9; для точки Мb1 при С=0,0001 ξ_Mb1=96 нм (фиг.6), для точки Мb2 при С=0,5 ξ_Mb2=121 нм (фиг.7), для точки Мb3 при С=0,9 ξ_Mb3=140 нм (фиг.8). Т.е. видно, что при увеличении уровня обратной связи происходит значительное смещение максимумов амплитуды первой гармоники по оси абсцисс ξ, в то время как по оси ординат 6 максимумы смещаются незначительно.

Таким образом, при наличии внешней оптической обратной связи амплитуда спектральной составляющей автодинного сигнала на частоте колебания объекта изменяется, как показано на фиг.6, 7, 8 и 9.

Для учета уровня внешней оптической обратной связи предложено построить зависимость S₁/S_1max от амплитуды вибраций ξ при различных уровнях внешней оптической обратной связи. Зависимости S₁/S_1max от ξ построены из соотношения для функции автодинного сигнала (1) при использовании ряда Фурье (5). Эти зависимости при разных уровнях обратной связи приведены на фиг.10.

Зависимости, представленные на фиг.10, построены при стационарном набеге фазы θ=0,5π, соответствующем максимальному значению первой гармоники спектра автодинного сигнала.

Способ реализуется следующим образом

Схема экспериментальной установки представлена на фиг.11. Освещают объект 3, закрепленный на пьезокерамике 4, излучением от полупроводникового лазера 1, записываемого от источника питания 2, преобразуют отраженное от объекта излучения в электрический сигнал с помощью фотодетектора 6, через фильтр переменного сигнала 7, усилитель 8 и аналого-цифровой преобразователь 9 подают сигнал на компьютер 10 и раскладывают в спектральный ряд, измеряют амплитуду гармоники спектра S_x на частоте колебания объекта Ω. Способ отличается тем, что на объект накладывают дополнительные механические колебания на частоте Ω₁ с помощью генератора звуковых колебаний 5, измеряют максимальное значение гармоники S_1max, на частоте Ω₁ при изменении амплитуды дополнительных механических колебаний, увеличивают амплитуду дополнительных механических колебаний до появления на автодинном сигнале интерференционных максимумов и минимумов на выделенном участке времени между точками, соответствующими крайним положениям смещения объекта, вычисляют отношение времени убывания t_dec автодинного сигнала ко времени его нарастания t_inc на выделенном участке времени, при этом, если значение t_dec/t_inc больше 1, то вычисляют t_inc/t_dec, по зависимости t_dec/t_inc(C) или t_inc/t_dec(C) определяют уровень внешней оптической обратной связи С, вычисляют S_x/S_1max, по зависимости S₁/S_1max(ξ, C) при определенном ранее С находят ξ.

Также ξ можно найти путем решения задачи оптимизации, заключающейся в нахождении наименьшего значения разности отношения S₁/S_1max, полученного с учетом измеренного С из соотношения для функции автодинного сигнала (1) при использовании ряда Фурье (5) при нановибрациях, и экспериментального отношения S_x/S_1max. В результате решения этой задачи находится искомое значение амплитуды нановибраций ξ.

Практическая реализация способа осуществлялась следующим образом.

С помощью генератора звуковых колебаний в пьезокерамике вызывались дополнительные механические вибрации, амплитуда которых изменялась во времени. Амплитуда дополнительных вибраций увеличивалась до тех пор, пока амплитуда первой гармоники спектра автодинного сигнала не достигала максимального значения, при котором фиксировался автодинный сигнал. При необходимости изменяют стационарный набег фазы излучения лазерного диода θ для получения максимального значения амплитуды первой гармоники. По спектру определялось максимальное значение амплитуды первой гармоники S_1max. На фиг.12 приведена форма измеренного автодинного сигнала при максимальном значении первой спектральной составляющей и его спектр фиг.13. Усредненное значение S_1max составило 0,131 отн. ед.

Для определения уровня обратной связи амплитуду дополнительных механических колебаний увеличивали до микрометровых значений. На фиг.14 приведена форма экспериментального автодинного сигнала при микровибрациях.

Усредненное отношение времени убывания ко времени нарастания составило 0,79. Такому отношению соответствует уровень внешней оптической обратной связи С=0,19 (фиг.5).

После исключения дополнительных механических колебаний измерялся автодинный сигнал вибраций объекта с неизвестной нанометровой амплитудой при вычисленном уровне обратной связи и известных параметрах S_1max и ξ_max. Форма и спектр измеренного автодинного сигнала приведены на фиг.15 и 16 соответственно. Усредненное значение амплитуды первой гармоники S_x составило 0,074 отн. ед. Отношение S_x/S_1max для приведенных экспериментальных автодинных сигналов составило величину 0,56.

Для полученного уровня обратной связи С=0,19 была построена зависимость S₁/S_1max от амплитуды вибрации ξ, представленная на фиг.17, кривая а17, по которой была определена амплитуда нановибраций для автодинного сигнала, приведенного на фиг.15, которая составила 30 нм. Без учета уровня внешней оптической обратной связи (фиг.17, кривая b17) измеренная описанным выше методом амплитуда нановибраций составила 36 нм.

Результаты измерений амплитуды нановибраций ξ с учетом уровня обратной связи и без его учета для различных уровней обратной связи приведены в таблице 1. Измерения проводились многократно с целью повышения достоверности. При вычислениях использовались усредненные значения измеренных величин. По результатам измерений при различных уровнях обратной связи среднее значение амплитуды нановибраций составило 29 нм.

Таблица I
Измеренный уровень обратной связи	Значение искомой амплитуды нановибраций ξ с учетом уровня обратной связи, nm	Значение амплитуды нановибраций ξ без учета уровня обратной связи, nm	Относительная погрешность определения амплитуды нановибраций δ без учета уровня обратной связи, %
С=0.19	30	36	24
С=0.39	27	40	38
С-0.53	30	52	79

Способ измерения амплитуды нановибраций, заключающийся в том, что освещают объект лазерным излучением, преобразуют отраженное от него излучение в электрический автодинный сигнал, раскладывают сигнал в спектральный ряд и измеряют значение амплитуды гармоники S_x на частоте колебания объекта Ω, отличающийся тем, что на объект накладывают дополнительные механические колебания на частоте Ω₁, измеряют максимальное значение гармоники S_1max, на частоте Ω₁ при изменении амплитуды дополнительных механических колебаний, увеличивают амплитуду дополнительных механических колебаний до появления на автодинном сигнале интерференционных максимумов и минимумов на выделенном участке времени между точками, соответствующими крайним положениям смещения объекта, вычисляют отношение времени убывания t_dec автодинного сигнала ко времени его нарастания t_inc на выделенном участке времени, при этом, если значение t_dec/t_inc больше 1, то вычисляют t_inc/t_dec, по зависимости t_dес/t_inc(С) или t_inc/t_dec(C) определяют уровень внешней оптической обратной связи С, вычисляют S_x/S_1max, по зависимости S₁/S_1max(ξ, C) при определенном ранее С находят амплитуду нановибраций ξ.