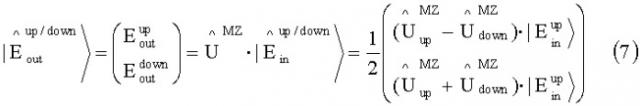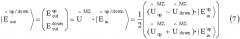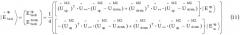Способ квантового кодирования и передачи криптографических ключей

Способ квантового кодирования и передачи криптографических ключей

Иллюстрации

Показать все

Реферат

Изобретение относится к области квантовой криптографии - системам квантового распределения криптографических ключей, а более конкретно, к способам квантового кодирования и передачи криптографических ключей. Системы квантовой криптографии позволяют не только обнаруживать любые попытки несанкционированного вторжения в канал связи, но и гарантировать безусловную секретность передаваемых криптографических ключей при условии, что ошибка на принимающей станции в первичных ключах не превышает некоторой критической величины.

Из уровня техники в данной области известен способ кодирования и передачи криптографических ключей, включающий привязку по времени квантовых состояний на передающей-принимающей и преобразующей станциях путем посылки в канал связи классических синхронизирующих лазерных импульсов, формирование в преобразующей станции серии однофотонных состояний при помощи фазовых преобразований, передачу однофотонных состояний по квантовому каналу связи на передающую-принимающую станцию, согласование базисов по открытому классическому каналу связи путем сообщения с передающей-принимающей станции на преобразующую станцию базисов для каждой посылки квантового состояния и детектирование на принимающей станции однофотонных состояний посредством фазовых преобразований однофотонных состояний (см. патент США №6.529.601 B1, кл. МКИ H04L 9/00, G02B 26/08, опубликованный 04.03.2003 г.). К принципиальным недостаткам известного способа, основанного на фазовых преобразованиях однофотонных состояний, которые требуют прецизионного контроля и управления, относится то, что диапазон допустимых ошибок в передаваемых ключах на передающей-принимающей станции, в котором гарантируется секретность передаваемых криптографических ключей, определяется искажениями поляризации лазерных и однофотонных импульсов, вызванных флуктуациями параметров оптоволоконных элементов и квантового канала связи. В силу указанных недостатков, известный способ использует фарадеевское зеркало, которое не позволяет обеспечить полномасштабную стабильность.

Технический результат, на достижение которого направлено изобретение, заключается в расширении диапазона возможных искажений поляризации лазерных и однофотонных импульсов при передаче ключей между передающей-принимающей и преобразующей станциями, в котором гарантируется секретность криптографических ключей и снятие условия использования специального фарадеевского зеркала.

Указанный технический результат достигается тем, что в предложенном способе для серии классических синхронизирующих лазерных импульсов на передающей-принимающей станции создают поляризационные состояния при помощи поляризационного контроллера в одном из плеч интерферометра и поляризационного контроллера на выходе интерферометра, обеспечивающие интерференционную балансировку интерферометра независимо от состояния канала связи, серию однофотонных состояний после отражения от зеркала в преобразующей станции детектируют на передающей-принимающей станции и по полученной статистике фотоотсчетов вычисляют допустимую ошибку, которую затем сравнивают с определенным пороговым значением ошибки для получения известного только на передающей-принимающей и преобразующей станциях криптографического ключа.

Сущность изобретения поясняется чертежами.

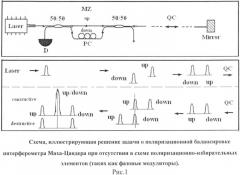
На рис.1 показана схема, иллюстрирующая решение задачи о поляризационной балансировке интерферометра Маха-Цандера при отсутствии в схеме поляризационно-избирательных элементов (таких, как фазовые модуляторы). На нижней части рис.1 показаны временные диаграммы однофотонных состояний для кодирования криптографических ключей при прямом (от передающей-принимающей к преобразующей станции) и обратном (от преобразующей к передающей-принимающей станции) проходах. Стрелки указывают направление движения импульсов.

На рисунке 1 используют следующие обозначения:

MZ - интерферометр Маха-Цандера,

50/50 - симметричные светоделители,

PC - контроллер поляризации,

Mirror - зеркало,

D - детектор фотонов,

QC - канал связи,

Constructive - режим конструктивной интерференции с максимумом в центральном временном окне,

Destructive - режим деструктивной интерференции с минимумом в центральном временном окне.

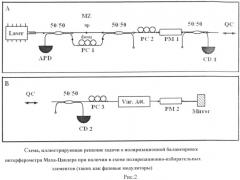
На рис.2 показана схема, иллюстрирующая решение задачи о поляризационной балансировке интерферометра Маха-Цандера при наличии в схеме поляризационно-избирательных элементов (таких, как фазовые модуляторы).

На рисунке 2 используют следующие обозначения:

А - передающая-принимающая станция,

В - преобразующая станция,

MZ - интерферометр Маха-Цандера,

РС (1, 2, 3) - контроллеры поляризации,

РМ (1,2) - поляризационно-избирательные элементы (фазовые модуляторы),

CD (1, 2) - классические фотодетекторы,

Mirror - зеркало,

APD - детектор фотонов,

50/50 - симметричные светоделители,

QC - канал связи,

Var. Att. - аттенюатор с переменным коэффициентом ослабления.

Классические информационные биты 0 и 1 кодируются в квантовые состояния фотонов при помощи протокола кодировки, в качестве которого выбирают любой известный протокол фазового кодирования.

На выходе из лазера длительность всех состояний равна δT - эту величину устанавливают много меньше задержки T, вводимой разбалансированным интерферометром. Отдельные импульсы лазера после прохождения интерферометра с разной длиной плеч преобразуются в пару состояний («up» - состояние, прошедшее по короткому верхнему пути, и «down» - состояние, соответственно, прошедшее по нижнему длинному пути). После прохождения канала связи отражения от зеркала состояния «up» и «down» меняются местами. На обратном проходе пара состояний, сдвинутых по времени, поступают на тот же интерферометр MZ, где пары состояний по верхнему и нижнему путям опять сдвигаются относительно друг друга. На выходе MZ состояние «up», прошедшее по верхнему пути, интерферирует с состоянием «down», прошедшим по нижнему пути. В зависимости от относительной фазы состояний «up» и «down» будет иметь место деструктивная интерференция - отсутствие отсчета на детекторе - либо конструктивная, приводящая к отсчету.

Если бы интерферометр MZ был идеальным, то на выходе возникала пара одинаковых состояний - с одинаковой поляризацией, сдвинутых по времени на величину разности хода по верхнему и нижнему пути Т. Дальнейшая эволюция пары одинаковых состояний через канал связи была бы также одинаковой. Деформационные и температурные изменения в канале связи за время Т, разделяющее «up» и «down» состояния, не успевают произойти, поскольку данное время составляет несколько наносекунд. Главная проблема состоит в том, как сделать, чтобы прохождение по двум путям интерферометра приводило на выходе к двум одинаковым состояниям.

Поскольку оптическое одномодовое волокно имеет деформации, то поляризационные состояния выходят разными и требуется балансировка интерферометра. Данная задача - решения, допускающие техническую реализацию и гарантирующие равенство состояний на выходе MZ.

Для дальнейшего удобно пользоваться дираковскими обозначениями. В этом случае состояния поля в базисе двух поляризаций, горизонтальной (Н) и вертикальной (V), представляют собой двухкомпонентный столбец

| E 〉 = α | E H 〉 + β | E V 〉 → ( α β ) ,                                     ( 1 )

где - | E H , V 〉 базисные состояния поляризации, α, β - комплексные коэффициенты - амплитуды базисных состояний.

Эволюция состояний является унитарной, поэтому общий вид матрицы оптического преобразования есть матрица группы SU(2). Трансфер-матрицу общего вида в базисе горизонтальной и вертикальной поляризаций, описывающую любой линейный оптический элемент, представляют в виде:

U ^ ( ϕ , δ , θ ) = ( cos ϕ − sin ϕ sin ϕ − cos ϕ ) ( e i δ   0 0     e i δ   ) ( cos θ − sin θ sin θ − cos θ )                       ( 2 )

Данное представление имеет прозрачный физический смысл. Правая матрица преобразований является матрицей поворота, которая приводит выбранный общий базис (НУ) для всей оптической схемы к главным осям элемента. Вторая матрица, после приведения к главным осям, описывает двояколучепреломление, при котором компоненты с разной поляризацией распространяются с разной скоростью и набирают различные дополнительные фазы ±δ. Третья (левая) матрица описывает обратный поворот главных оптических осей данного оптического элемента к общей системе координат всей схемы.

Преобразование состояний в интерферометре Маха-Цандера и в канале связи. Состояние канала постоянно меняется, и каждый раз на интерферометр возвращается разная пара состояний. Прохождение туда и обратно не приводит к компенсации изменений состояний. Формальная причина связана с тем, что если эволюция состояний на прямом проходе описывается некоторой унитарной матрицей U ^ , то обратное прохождение (в той же системе координат) описывается транспонированной унитарной матрицей U T ^ . Физическая причина появления транспонированной матрицы на обратном проходе связана с тем, что положительно-частотные состояния поля с противоположными значениями волнового вектора связаны транспонированной матрицей, поэтому их произведение, описывающее эволюцию при прямом и обратном проходах, не является (при наличии двулучепреломления) единичной матрицей U^TU≠I. Известно, что оптическое одномодовое волокно при наличии механических напряжений и температурной нестабильности неизбежно обладает двулучепреломлением. В системах квантового распределения ключей, основанных на фазовом кодировании, принципиально используются элементы, выполненные на основе оптического одномодового волокна. Кроме того, в некоторых системах из такого волокна изготавливают и сам (квантовый) канал связи. Поэтому важной задачей является компенсация поляризационных искажений лазерных и квантовых состояний, распространяющихся по одномодовому оптическому волокну с целью минимизации ошибок, возникающих при регистрации квантовых состояний.

Для этого необходимо добиться, чтобы после выхода состояний из интерферометра Маха-Цандера и прохождения через канал связи на прямом и обратном проходах на входе детекторов D или APD независимо от состояния канала связи осуществлялась деструктивная интерференция (гашение квантовых состояний) - отсутствие отсчетов независимо от изменения состояния самого канала связи. Для достижения этой цели приведем два решения, составляющие суть данного изобретения.

1) Сначала покажем условия (Решение 1), при которых идеальное гашение интерференции будет иметь место при любых изменениях состояний в канале связи за счет упомянутых факторов. Это значит, что при определенной балансировке интерферометра деструктивная интерференция вообще не будет зависеть от изменений в канале связи и входного состояния. Данное решение не зависит и не использует факт присутствия поляризационно-избирательных элементов.

2) Затем приведем второе решение (Решение 2), обеспечивающее идеальное гашение интерференции независимо от входного состояния и канала связи. Это решение предопределяет простой способ балансировки интерферометра, включая автоматический способ. Данное решение явно использует неизбежное наличие в оптической схеме поляризационно-избирательных элементов (таких, как фазовые модуляторы). Присутствие этих элементов является необходимым атрибутом автоматической балансировки интерферометра. Данные условия обеспечиваются тем, что если из интерферометра выходят одинаковые квантовые состояния, то дальнейшие их изменения в канале связи также будут одинаковыми. Несмотря на то, что на интерферометр возвращаются другие состояния, по сравнению с теми, которые были на его выходе при прямом проходе, тем не менее все равно гарантируется точное гашение интерференции в центральном (информационном) временном окне (см. нижнюю часть рис.1) и отсутствие ошибок, связанных с изменениями состояния квантового канала связи.

Нетривиальность процедуры балансировки заключается в том, что достаточно только одного измерения интегральной интенсивности поля в двух временных окнах, прошедшего по верхнему и нижнему пути интерферометра на прямом проходе классическим фотодетектором CD1 в режиме интенсивного сигнала лазера.

Докажем сначала первую часть утверждения, а затем приведем способ автоматической балансировки для второго решения. Для этого потребуются матрицы преобразований оптических элементов.

1. Матрица преобразования для светоделителя 50/50 имеет вид:

U ^ 50 / 50 ( 1 ) = 1 2 ( I ^ − I ^ I ^ I ^ ) ,             U ^ 50 / 50 ( 2 ) = 1 2 ( I ^ − I ^ I ^ I ^ )               ( 3 )

2. Матрицы преобразований по различным путям интерферометра.

Трансфер-матрица верхнего («up») и нижнего («down») путей в интерферометре Маха-Цандера (MZ):

U ^ u p / d o w n M Z = ( U ^ u p M Z 0 0 U ^ d o w n M Z )                                         ( 4 )

Полная трансфер-матрица интерферометра MZ равна:

U ^ M Z = U ^ 50 / 50 ( 2 ) U ^ u p / d o w n M Z ⋅ U ^ 50 / 50 ( 1 )                                         ( 5 )

Состояния поля в двух каналах «up» и «down» равны:

| E i n u p 〉 = ( E H u p E V u p ) ,   | E i n d o w n 〉 = ( E H d o w n E V d o w n ) ,   | E i n u p / d o w n 〉 = ( E H u p E V d o w n )                                   ( 6 )

Выходное поле:

| E ^ o u t u p / d o w n 〉 = ( E o u t u p E o u t d o w n ) = U ^ M Z ⋅ | E ^ i n u p / d o w n 〉 = 1 2 ( ( U ^ u p M Z − U ^ d o w n M Z ) ⋅ | E i n u p 〉 ( U ^ u p M Z + U ^ d o w n M Z ) ⋅ | E i n u p 〉 )                 ( 7 )

Для амплитуд поля в верхнем канале на выходе MZ (после отбрасывания холостого выхода) получают:

| E i n u p 〉 = ( | E o u t u p 〉 0 ) = 1 2 ,   | E i n d o w n 〉 = ( ( U ^ u p M Z − U ^ d o w n M Z ) ⋅ | E i n u p 〉 0 )                             ( 8 )

3. Матрицы зеркал. Отражение от зеркала (М) и фарадеевского зеркала (FM) дается матрицами

M R ∧ M = ( − 1 0 0 − 1 ) ,       M R ∧ F M = ( 0 − 1 1 0 )                                   ( 9 )

Фарадеевское зеркало при отражении меняет компоненты поляризации по правилу Н↔V.

4. Матрицы преобразования полей в канале связи. Пусть трансфер-матрица канала связи есть U ^ c h . При обратном проходе матрицы преобразования даются транспонированными. После прохождения через канал отражения от зеркала и обратного прохождения через канал для поля перед входом в интерферометр имеем (m=М или m=FM)

U ^ ↔ = U ^ c h T ⋅ M R ∧ m ⋅ U ^ c h                                                   ( 10 )

Обратное прохождение через интерферометр дается трансфер-матрицей ( U ^ M Z ) T . Для амплитуд поля на верхнем и нижнем выходах интерферометра находим

| E ^ b a c k u p 〉 = ( E b a c k u p E b a c k d o w n ) = 1 4 ( [ ( U ^ u p M Z ) T ⋅ U ^ ↔ ⋅ ( U ^ u p M Z − U ^ d o w n M Z ) + ( U ^ d o w n M Z ) T ⋅ U ^ ↔ ⋅ ( U ^ u p M Z − U ^ d o w n M Z ) ] ⋅ | E i n u p 〉 [ − ( U ^ u p M Z ) T ⋅ U ^ ↔ ⋅ ( U ^ u p M Z − U ^ d o w n M Z ) + ( U ^ d o w n M Z ) T ⋅ U ^ ↔ ⋅ ( U ^ u p M Z − U ^ d o w n M Z ) ] ⋅ | E i n u p 〉 )                 ( 11 ) Амплитуда поля в центральном временном окне при интерференции состояний «up» (прямой проход)=>«down» (обратный проход) и «down» (прямой проход)=>«up» (обратный проход) проходы имеет вид

1 4 ( [ ( U ^ u p M Z ) T ⋅ U ^ ↔ ⋅ U ^ d o w n M Z ) + ( U ^ d o w n M Z ) T ⋅ U ^ ↔ ⋅ U ^ u p M Z ] ⋅ | E i n u p 〉 [ ( U ^ u p M Z ) T ⋅ U ^ ↔ ⋅ U ^ d o w n M Z ) + ( U ^ d o w n M Z ) T ⋅ U ^ ↔ ⋅ U ^ u p M Z ] ⋅ | E i n u p 〉 )                 ( 12 )

Решение 1. Если трансфер-матрицы для состояний поляризации по верхнему и нижнему путям равны (с точностью до общего фазового множителя e i ψ L перед матрицей, связанного с разной длин плеч, который без ограничения общности, далее опускаем) U ^ u p M Z = U ^ d o w n M Z = U ^ M Z , то равны и транспонированные матрицы ( U ^ u p M Z ) T = ( U ^ d o w n M Z ) T = ( U ^ M Z ) T , тогда независимо от входного состояния, состояния канала и типа зеркала имеет место идеальная деструктивная интерференция. Амплитуда состояния на выходе детектора фотонов тождественно равна нулю. Это гарантируется для любого состояния условием равенства матриц преобразований по верхнему и нижнему пути в интерферометре

U ^ u p M Z = U d o w n M Z = U ^ M Z ,                               ( 13 )

тогда

| Е b a c k d o w n 〉 = [ ( U ^ M Z ) T ⋅ U ^ ↔ ⋅ U ^ M Z − ( U ^ M Z ) T ⋅ U ^ ↔ ⋅ U ^ M Z ] ⋅ | E i n u p ≡ 0 〉 .                 ( 14 )

Данное решение является универсальным в том смысле, что обеспечивает идеальное гашение интерференции независимо от присутствия других оптических элементов в схеме (поляризационно-избирательных фазовых модуляторов, контроллеров поляризации и отражающих зеркал). Однако не существует простого алгоритма достичь равенства матриц преобразования по двум путям, используя управляющие элементы - контроллеры поляризации.

Решение 2. Способ балансировки интерферометра. Это решение обеспечивает гашение интерференции независимо от входного/выходного квантового состояния и состояния самого канала связи. В данном решении явно используют факт присутствия в оптической схеме поляризационно-избирательных элементов - фазовых модуляторов (см. рис.2). Такие элементы технологически устроены так, что пропускают состояния только с одним направлением поляризации, которая зависит от оси ориентации поляризационно-избирательного элемента.

При дальнейшем описании в качестве поляризационно-избирательных элементов будем рассматривать фазовые модуляторы. Матрица, описывающая действие фазового модулятора, является проектором на определенное состояние поляризации. Пусть состояние, отвечающее направлению поляризации, которое пропускает фазовый модулятор, равно | E 1 | | 〉 , соответственно перпендикулярному направлению, которое не пропускает фазовый модулятор - состояние | E 1 ⊥ 〉 . Действие фазового модулятора в отсутствие приложенного напряжения на нем в базисе | E 1 | | 〉 , | E 1 ⊥ 〉 описывают проектором

U ^ P M 1 = | E 1 | | 〉 〈 E 1 | | .                                   ( 15 )

Пусть состояния после контроллера поляризации РС2, происходящие из состояний, прошедших по верхнему и нижнему пути интерферометра, имеют вид:

| E u p 〉 = U ^ u p P C 2 | E i n 〉 = U ^ P C 2 U ^ u p M Z | E i n 〉 ,         E d o w n 〉 = U ^ d o w n P C 2 | E i n 〉 = U ^ P C 2 U ^ d o w n M Z | E i n 〉 ,     ( 16 )

где U ^ P C 2 - трансфер-матрица, описывающая некоторое текущее состояние контроллера поляризации. В дальнейшем под контроллером поляризации будем понимать устройство, которое обеспечивает унитарное (без потерь) преобразование входного состояния поляризации света в любое наперед заданное (произвольное) выходное состояние поляризации. Действие контроллера поляризации описывают унитарным оператором. На данном этапе матрицы перехода по верхнему («up») и нижнему («down») путям интерферометра MZ считают фиксированными.

Этап 1. Регулируя состояние РС2 (см. рис.2), добиваются равенства нулю интенсивности на фотодетекторе CD2 во временном окне, накрывающем состояние, прошедшее по верхнему («up») пути интерферометра - пути, не содержащему контроллера поляризации РС1. Такую эволюцию описывают унитарным оператором, который в двумерном пространстве имеет вид:

U ^ u p P C 2 ( ⊥ ) = U ^ P C 2 ( ⊥ ) U ^ u p M Z = | E