Способ дистанционного определения крутизны склона в контрольных точках лавинного очага с использованием лазерного дальномера

Способ дистанционного определения крутизны склона в контрольных точках лавинного очага с использованием лазерного дальномера

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области метеорологии и гляциологии, а именно к способам дистанционного определения крутизны склона в лавинных очагах, и может быть использовано при определении толщины снежного покрова на склонах для прогноза лавинной опасности и определения снегонакопления в горах.

Крутизна склона является одной из важнейших морфометрических характеристик рельефа. Согласно определению крутизна склона - это вертикальный угол, образованный направлением склона горы, оврага, берега реки и т.п. с горизонтальной плоскостью в данной точке, выражаемый в градусах.

Известны различные способы определения крутизны склона в горах с помощью компаса и простейшего угломера [1].

При определении крутизны склона наиболее приемлем простейший угломер. Он представляет собою жесткое основание, на котором закреплен транспортир и отвес с грузом. При замере углов наклона поверхности к горизонту одну из сторон основания выставляют параллельно поверхности склона и по положению отвеса относительно шкалы транспортира определяют крутизну склона в заданной точке.

Недостатком известных способов является то, что при использовании таких приборов как компас и угломер, можно получить только среднее значение измеряемой величины. Известные способы не приемлемы для определения крутизны склона при наличии глубокого снежного покрова на склоне, да еще при наличии серьезной опасности, связанной со сходом лавин. В этих случаях необходимы только дистанционные измерения.

Наиболее близким по технической сущности к заявленному объекту является способ дистанционного определения параметров склона и снежного покрова в лавинных очагах с использованием лазерной локации. Задача этих съемок - получение высокоточных цифровых моделей рельефа поверхности земли и поверхности снежного покрова [2].

К недостаткам известного способа можно отнести высокую стоимость авиационной техники и невозможность ее использования при снегопадах, что затрудняет реализацию способа для целей активного воздействия.

Техническим результатом, ожидаемым от использования заявленного способа, является снижение трудозатрат по его реализации и повышение точности дистанционного измерения крутизны склона в лавинных очагах с использованием лазерного дальномера.

Технический результат достигается тем, что в известном способе дистанционного определения крутизны склона в контрольных точках лавинного очага с использованием лазерного дальномера, согласно изобретению сначала с помощью лазерного дальномера, размещенного в долине, определяют расстояние до произвольной контрольной точки «А» на склоне (L₁), угол зондирования (β₁) и азимут проекции лазерного луча на горизонтальную плоскость (A₁), затем, сместив зондирующий луч по вертикали вниз, для второй произвольной (вспомогательной) точки «В», лежащей на некотором расстоянии «АВ» от контрольной точки «А» на склоне, определяют расстояние (L₂) и угол зондирования (β₂), затем, используя найденные значения величин L₁, L₂, β₁ и β₂, из соотношения сторон и углов геометрических фигур (треугольников), образованных в вертикальной плоскости, проходящей по линии зондирования, определяют проекцию отрезка «АВ» на горизонтальную плоскость, и высоту стояния контрольной точки «А» от вспомогательной точки «В» на склоне, затем определяют проекцию на горизонтальную плоскость нормали склона ( n ¯ ) в контрольной точке «А» и угол α между данной проекцией и проекцией на горизонтальную плоскость отрезка «АВ», соединяющего контрольную (А) и вспомогательную «В» точки на склоне, затем вычисляют крутизну склона (β) по формуле β = a r c t g [ L 1 ⋅ sin β 1 − L 2 ⋅ sin β 2 ( L 1 ⋅ cos β 1 − L 2 ⋅ cos β 2 ) ⋅ cos α ]

где

L₁·cosβ₁-L₂·cosβ₂ - высота стояния контрольной точки «А» над вспомогательной точкой «В» на склоне;

L₁·sinβ₁-L₂·sinβ₂ - проекция отрезка «АВ» на горизонтальную плоскость.

Технический результат достигается и тем, что при определении угла α, предварительно сместив зондирующий луч от контрольной точки «А» на некоторое расстояние по горизонтали влево (или вправо), определяют расстояние «L_Z» до второй, произвольной вспомогательной точки «Z» на склоне и азимут зондирования этой точки (A_z), после чего в соответствующем масштабе строят проекцию на горизонтальную плоскость величин L₁, L_Z и отрезка «AZ» и, проведя к проекции отрезка «AZ» перпендикуляр, находят проекцию на горизонтальную плоскость нормали ( n ¯ ), затем с помощью угломера определяют угол α между данной проекцией и проекцией величины L₁ на горизонтальную плоскость.

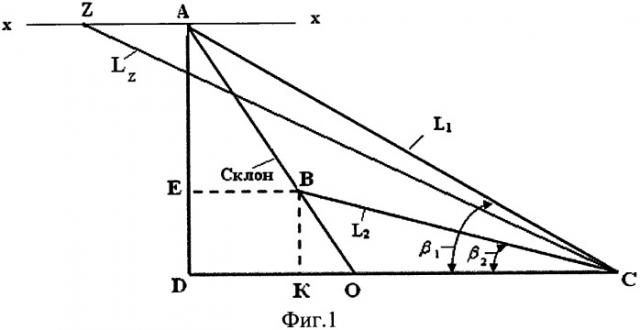
На фиг.1 представлена схема зондирования контрольной «А» и вспомогательной «В» точек на склоне.

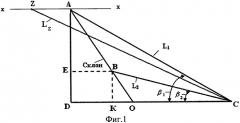
На фиг.2 представлена проекция на горизонтальную плоскость величин L₁ L₂ и отрезка AZ, соединяющего контрольную «А» и вспомогательную точку «Z», лежащую на одной горизонтали с точкой «А».

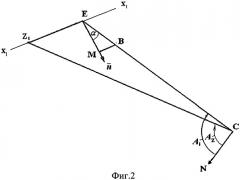
На фиг.3 представлена схема расчета угла «α» между проекциями на горизонтальную плоскость нормали « n ¯ » и отрезка «АВ», соединяющего контрольную «А» и вспомогательную точку «В» на склоне.

На фиг.1 приняты следующие обозначения:

АО - склон;

L₁ и L₂ - расстояние, измеренное лазерным дальномером, соответственно, до контрольной (А) и вспомогательной (В) точек на склоне;

β₁ и β₂ - угол зондирования соответственно точек «А» и «В» на склоне;

АЕ - высота стояния контрольной точки «А» от вспомогательной точки «В» на склоне;

ЕВ - проекция отрезка «АВ» на горизонтальную плоскость;

«х-х» - горизонталь, проходящая через контрольную точку «А» на склоне;

DC - проекция отрезка L₁ на горизонтальную плоскость;

КС - проекция отрезка L₂ на горизонтальную плоскость;

Z - произвольная вспомогательная точка, лежащая на некотором расстоянии от точки «А» по горизонтали;

х-х - горизонталь.

На фиг.2 приняты следующие обозначения:

Z₁ - проекция произвольной вспомогательной точки Z на горизонтальную плоскость;

Z₁C - проекция расстояния L_Z на горизонтальную плоскость;

A₁ - азимут зондирования точек «А» и «В» на склоне;

A_z - азимут зондирования вспомогательной точки «Z» на склоне;

n ¯ - проекция нормали склона на горизонталь «x-x»;

Стрелкой «N» обозначено направление на Север;

x₁-x₂ - проекция горизонтали (x-x) на горизонтальную плоскость.

На фиг.3 приняты следующие обозначения:

ЕВ - проекция отрезка «АВ» на горизонтальную плоскость;

ЕМ - проекция отрезка ЕВ на нормаль « n ¯ » в горизонтальной плоскости;

АЕ - высота стояния контрольной точки «А» относительно вспомогательной точки «В» на склоне;

α - угол между проекциями на горизонтальную плоскость отрезка «ЕВ» и нормали « n ¯ ».

Предлагаемый способ реализуется следующим образом:

1) Предварительно в долине в точке «С», с которой хорошо просматривается контрольная точка «А» на склоне (фиг.1), устанавливается система измерений (теодолит с лазерным дальномером).

2) Затем с помощью лазерного дальномера определяют расстояние (L₁) до контрольной точки «А» на склоне, азимут (A₁) и угол зондирования (β₁).

3) После чего, сместив зондирующий луч на некоторое расстояние АВ по вертикали вниз (или вверх), определяют расстояние (L₂) до произвольной вспомогательной точки (В) на склоне. Угол смещения в зависимости от дальности составляет примерно 0,5-5°.

4) После чего, используя найденные значения величин L₁, L₂, β₁ и β₂ из соотношения сторон и углов треугольников, образованных в вертикальной плоскости (фиг.1), проходящей по линии зондирования, определяют проекцию отрезка «АВ» на горизонтальную плоскость

ЕВ=L₁·cosβ,-L₂·cosβ₂

и высоту стояния контрольной точки «А» от вспомогательной точки «В» на склоне по формуле

АЕ=L₁·sinβ,-L₂·sinβ₂.

5) Затем находят проекцию на горизонтальную плоскость нормали склона ( n ¯ ) в контрольной точке «А» и угол α между данной проекцией и проекцией на горизонтальную плоскость отрезка «АВ», соединяющего контрольную «А» и вспомогательную «В» точки на склоне. Для этого, предварительно сместив зондирующий луч от контрольной точки «А» на некоторое расстояние по горизонтали влево (или вправо), определяют расстояние «L_Z» до второй, произвольной вспомогательной точки «Z» на склоне и азимут зондирования этой точки (A_Z). После этого в соответствующем масштабе строят проекцию на горизонтальную плоскость величин L₁, L_Z и отрезка «AZ» (фиг.2). Затем по изложенной выше методике находят проекцию на горизонтальную плоскость нормали ( n ¯ ) и с помощью угломера определяют угол α между данной проекцией и проекцией величины L₁ на горизонтальную плоскость.

6) После этого вычисляют крутизну склона в контрольной точке «А» по приведенной выше формуле.

β = a r c t g [ L 1 ⋅ sin β 1 − L 2 ⋅ sin β 2 ( L 1 ⋅ cos β 1 − L 2 ⋅ cos β 2 ) ⋅ cos α ] .

Пример выполнения способа В результате зондирования контрольной точки «А» на склоне были получены следующие результаты:

-расстояние до контрольной точки L₁=1800 м;

-азимут A₁=120°;

-угол зондирования β₁=12°.

После этого, сместив зондирующий луч на некоторое расстояние по вертикали вниз от точки «А», выбрали произвольную вспомогательную точку «В» на склоне. В результате зондирования данной точки «В» на склоне были получены следующие результаты:

-расстояние до вспомогательной точки L₂=900 м;

-азимут зондирования точки «В» равен азимуту зондирования точки «А» и равен 120°. В тексте и на фигуре данный азимут обозначен через A₁);

-угол зондирования β=9°.

Затем нашли проекцию на горизонтальную плоскость отрезка АВ по формуле

ЕВ=(L₁·cosβ₁-L₂·cosβ₂)=1800·cos12-900·cos9=871,75 м,

и высоту стояния контрольной точки «А» от вспомогательной точки «В» на склоне по формуле

AE=L₁·sinβ₁-L₂·sinβ₂=1800·sin12-900·sin9=233,45 м.

После построения в соответствующем масштабе на горизонтальную плоскость проекций величин L₁, L₂ и отрезка «AZ», с помощью угломера нашли угол α=30 град.

Зная значение угла α, нашли крутизну склона

β = a r c t g [ L 1 ⋅ sin β 1 − L 2 ⋅ sin β 2 ( L 1 ⋅ cos β 1 − L 2 ⋅ cos β 2 ) ⋅ cos α ] = a r c t g 233,45 871,75 ⋅ 0,86 = 17,43  град .

Для случая, когда луч лазерного дальномера смещают вверх от контрольной точки, расчеты производятся аналогичным способом, полагая при этом, что вспомогательная (верхняя) точка является контрольной, а нижняя точка - вспомогательной, что упрощает процедуру расчета.

Предлагаемый способ в отличие от известных существенно снижает трудоемкость операций и повышает точность дистанционного измерения экспозиции склона в лавинных очагах с использованием лазерного дальномера.

Источники информации

1. Алешин В.М., Серебрянников А.В. Туристская топография (раздел Измерение высот и крутизны склонов на местности). - М.: Профиздат, 1985, - 160 с.

2. Бойко Е.С.Использование метода воздушной лазерной локации при оценке снегонакопления в горных условиях // Материалы VI международной конференции. «Лазерное сканирование и цифровая аэросъемка. Сегодня и завтра». - М., 2006. С.29-30. - ПРОТОТИП.

3. Алексеев А. А. Горообразование и горный рельеф (пособие для инструкторов и преподавателей туризма), издание второе. - М., 2002, - 40 с.

1. Способ дистанционного определения крутизны склона в контрольных точках лавинного очага с использованием лазерного дальномера, отличающийся тем, что с помощью лазерного дальномера, размещенного в долине, сначала определяют расстояние до произвольной контрольной точки «А» на склоне (L₁), угол зондирования (β₁) и азимут проекции лазерного луча на горизонтальную плоскость (A₁), затем, сместив зондирующий луч по вертикали вниз, для второй произвольной (вспомогательной) точки «В», лежащей на некотором расстоянии «АВ» от контрольной точки «А» на склоне, определяют расстояние (L₂) и угол зондирования (β₂), затем, используя найденные значения величин L₁, L₂, β₁ и β₂, из соотношения сторон и углов геометрических фигур (треугольников), образованных в вертикальной плоскости, проходящей по линии зондирования, определяют проекцию отрезка «АВ» на горизонтальную плоскость и высоту стояния контрольной точки «А» от вспомогательной точки «В» на склоне, затем определяют проекцию на горизонтальную плоскость нормали склона ( n ¯ ) в контрольной точке «А» и угол α между данной проекцией и проекцией на горизонтальную плоскость отрезка «АВ», соединяющего контрольную (А) и вспомогательную «В» точки на склоне, затем вычисляют крутизну склона (β) по формуле β = a r c t g [ L 1 ⋅ sin β 1 − L 2 ⋅ sin β 2 ( L 1 ⋅ cos β 1 − L 2 ⋅ cos β 2 ) ⋅ cos α ] , гдеL₁·sinβ₁-L₂·sinβ₂ - высота стояния контрольной точки «А» над вспомогательной точкой «В» на склоне;L₁·cosβ₁-L₂·cosβ₂ - проекция отрезка «АВ» на горизонтальную плоскость.

2. Способ дистанционного определения крутизны склона в контрольных точках лавинного очага по п.1, отличающийся тем, что при определении проекции на горизонтальную плоскость нормали ( n ¯ ) угла α, предварительно сместив зондирующий луч от контрольной точки «А» на некоторое расстояние по горизонтали влево (или вправо), определяют расстояние «L_Z» до второй произвольной вспомогательной точки «Z» на склоне и азимут зондирования этой точки (A_z), затем в соответствующем масштабе строят проекцию на горизонтальную плоскость величин L₁, L_Z и отрезка «AZ» и, проведя к проекции отрезка «AZ» перпендикуляр, находят проекцию на горизонтальную плоскость нормали ( n ¯ ), затем с помощью угломера измеряют угол α между данной проекцией и проекцией величины L₁ на горизонтальную плоскость.