Способ ускорения макрочастиц

Способ ускорения макрочастиц

Иллюстрации

Показать все

Реферат

Изобретение относится к области ускорительной техники и может быть использовано для решения научных и прикладных задач, в частности для создания потока искусственных микрометеоритов, удаления космического мусора и в военном деле.

Область техники

Известен, [1], способ ускорения макрочастиц, сферической формы, заключающийся в том, что макрочастицы электрически заряжают контактным способом и заряженные частицы ускоряют электростатическим полем. Энергия макрочастиц в нем мала и ограничена высоковольтным потенциалом на кондукторе. Реально напряжение на кондукторе не может быть существенно больше, чем 3 MV, соответственно эти макрочастицы можно использовать только в вакууме. В условиях земной атмосферы такие макрочастицы быстро потеряют свою скорость из-за сопротивления воздуха их движению.

Известен, [2], способ ускорения макрочастиц сферической формы в спиральном волноводе, при котором: макрочастицы электрически заряжают, предварительно ускоряют электростатическим способом до скорости, соответствующей скорости инжекции, и окончательно ускоряют бегущим в спиральном волноводе импульсом, который может быть выбран за прототип.

Недостатки прототипа

Однако известному способу ускорения макрочастиц сферической формы с массой порядка нескольких грамм присущи два принципиальных недостатка: низкий темп ускорения и неспособность таких макрочастиц пересечь земную атмосферу, особенно при горизонтально расположенном ускорителе.

Действительно, масса сферической макрочастицы растет с ростом диаметра шара как куб диаметра. Площадь сферы, на которой располагаются избыточные заряды, помещенные на шар, растет как квадрат диаметра. Следовательно, отношение избыточных зарядов, размещенных на шаре, к его массе будет уменьшаться с ростом диаметра сферы. Это будет приводить к уменьшению параметра Z/A, где Z - размещенный на шаре электрический заряд, А - атомная масса шара, и снижению эффективности ускорения.

Для того чтобы лучше понять принципиальные недостатки ускорения частиц сферической формы, составим сравнительную Таблицу 1 основных параметров ускоряемых шариков в зависимости от их диаметра для случая железных шариков.

Таблица 1
Основные параметры ускоряемых сферических макрочастиц
Dsp, µ	А	Z	Z/A	еФ, MeV	M, g	βi
2	2*1013	6*107	3*10-6	0.1	3.2*10-11	4*10-5
20	2*1016	6*109	3*10-7	1	3.2*10-8	1.2*10-5
200	2*1019	6*1011	3*10-8	10	3.2*10-5	4*10-6
2*103	2*1022	6*1013	3*10-9	102	3.2*10-2	1.2*10-6

Во всех случаях напряженность электрического поля на поверхности шариков составляет величину E_surf=10⁹ V/cm. В первом столбце расположен D_sp - диаметр шарика в микронах, во втором столбце А - атомная масса шарика в единицах атомной массы нуклона, в третьем столбце находится заряд Z, посаженный на шарик в единицах заряда электрона, в четвертом столбце Z/A - отношение заряда, расположенного на шарике, к его массе, в пятом столбце потенциал Ф шарика - энергия, которую должен иметь электрон, чтобы преодолеть отталкивание ранее размещенных на шарике электронов, в шестом М - масса шарика в граммах, в седьмом β_sp - начальная скорость шариков, приобретенная ими после ускорения в электростатическом поле с напряжением U_inj=250 kV, выраженная в единицах скорости света: β_sp=V_sp/c, где с=3*10⁵ km/s, скорость света в вакууме.

Из сравнения данных, приведенных в Таблице 1, видно, что при увеличении диаметра шариков атомный вес и масса (столбцы 1, 6) растут как куб радиуса, как квадрат радиуса увеличивается необходимый заряд, который надо разместить на шарике для достижения напряженности поля E_surf=10 V/cm. Отношение заряда, размещенного на шарике к его массе, (столбец 4), линейно уменьшается с увеличением диаметра, и это значит, что с ростом диаметра линейно уменьшается эффективность ускорения, то есть в поле одной и той же напряженности, при одной и той же длине ускорителя, шарики большего диаметра наберут меньшую скорость.

Если перейти к ускорению пустотелых шариков, у которых практически вся масса сосредоточена в оболочке, то тогда с ростом диаметра и площадь поверхности, на которой располагаются избыточные заряды, и масса макрочастицы будут расти квадратично. Однако квадратично с ростом диаметра будет расти и площадь поперечного сечения макрочастицы сферической формы, так что сила торможения со стороны воздуха, приходящаяся на единицу массы, будет оставаться неизменной.

Так что пустотелые макрочастицы сферической формы тем более по сравнению со сплошными макрочастицами будут не способны проникнуть сквозь земную атмосферу. Это хорошо известно из бытовых представлений, метеоритный дождь - это сгорающие в атмосфере микрометеориты. Физически это объясняется тем, что коэффициент аэродинамического сопротивления для тел сферической формы близок к единице, [3], и их скорость в плотных слоях атмосферы быстро уменьшается.

Коэффициент аэродинамического сопротивления для сферы не зависит от ее диаметра и для гиперзвуковых скоростей, [3], остается практически постоянным и большим, порядка единицы.

Для макрочастиц цилиндрической формы, при неизменном поперечном сечении, сила торможения со стороны воздуха, приходящаяся на единицу массы, при увеличении длины цилиндра будет уменьшаться.

Эмпирическая формула для коэффициента аэродинамического сопротивления острого конуса, [4], квадратично зависит от угла раствора конуса при вершине, величиной угла при вершине конуса этот коэффициент можно изменять, и при малом угле при вершине конуса коэффициент аэродинамического сопротивления может быть много меньше единицы.

Техническая задача, которую решает данный способ, состоит в устранении указанных недостатков, то есть в увеличении темпа набора энергии макрочастицами при ускорении в спиральном волноводе и создании условий, позволяющих макрочастицам проникать сквозь атмосферу без фатальной потери скорости при горизонтально расположенном ускорителе.

Сущность настоящего изобретения заключается в том, что в данном способе ускорения макрочастиц их предварительно ускоряют до скорости, соответствующей скорости инжекции в спиральный волновод, макрочастицы облучают пучком электронов, инжектированных из электронного ускорителя, электрически их заряжая, и окончательно ускоряют макрочастицы полем бегущего по виткам спирального волновода электрического импульса, при этом макрочастицы имеют цилиндрическую форму с острым конусом в головной части, угол раствора конуса Θ≈0.1, имеющим небольшую асимметрию, приводящую к созданию подъемной силы, С_у=2.5*10^-2, так что коэффициенты аэродинамического сопротивления С_х и подъемной силы C_y примерно равны С_х≈C_y и по абсолютному значению составляют величину, много меньшую единицы, C_xC_y≈1.

Связь отличительных признаков с положительным эффектом

1. Электростатические соотношения

Составим сравнительные Таблицы 2, 3, где соберем основные параметры ускоряемых макрочастиц цилиндрической формы, в зависимости от диаметра и длины цилиндра для той же поверхностной напряженности поля: Е=10^-9 V/cm.

Прежде всего выясним, как зависит размещенный на цилиндрическом отрезке электрический заряд от диаметра цилиндра. Составим сравнительную Таблицу 2 параметров объектов для нескольких диаметров проводника при одной и той же длине проводника: l=10 mm. Таблица составлена для одной и той же поверхностной напряженности поля: Е=10⁹ V/cm.

Таблица 2
Сравнительные параметры макрочастиц цилиндрической формы
Диаметр dsh, µ	А	Z	Z/A	еФ, MeV	M, g	βi
2	1.5*1017	3*1011	2*10-6	0.92	2.5*10-7	3.16*10-5
20	1.5*1019	3*1012	2*10-7	6.9	2.5*10-5	10-5
200	1.5*1021	3*1013	2*10-8	46	2.5*10-3	3.16*10-6

Видно, что с ростом диаметра цилиндра линейно уменьшается очень важный для ускорения макрочастиц параметр Z/A, характеризующий эффективность ускорения. Быстро растет потенциал цилиндрического отрезка, то есть требуется все более высокая энергия электронов, чтобы преодолеть отталкивание ранее размещенных на отрезке цилиндра частиц. Поэтому диаметр цилиндра надо выбирать по возможности малым.

Составим сравнительную Таблицу 3, где сравнение с объектами сферической формы будем проводить для объектов цилиндрической формы с диаметром цилиндра d=20 микрон, для двух значений длины: l=2 mm и l=10 mm. Так же, как и в Таблице 1, для всех случаев напряженность электрического поля на поверхности объектов составляет величину Е=10⁹ V/cm. В первом столбце расположена длина 1 - отрезка в миллиметрах для одного и того же значения d=20 микрон - диаметра цилиндра. Во втором столбце приведена А - атомная масса цилиндра в единицах атомной массы нуклона, в третьем столбце находится заряд Z, который должен быть посажен на макрочастицу для достижения напряженности поля Е=10⁹ V/cm, выраженный в единицах заряда электрона, в четвертом столбце Z/A - отношение заряда, расположенного на цилиндре к его массе, в пятом столбце М - масса отрезка цилиндра, выраженная в граммах.

Таблица 3
Основные параметры ускоряемых макрочастиц цилиндрической формы
dsh=20 µ	A	Z	Z/A	M, g
l=2 mm	3*1018	6*1011	2*10-7	5*10-6
l=10 mm	1.5*1019	3*1012	2*10-7	2.5*10-5

Из сравнения данных, приведенных в Таблице 3, видно, что масса и заряд, размещенные на цилиндре, растут линейно с длиной. Таким образом, параметр Z/A - отношение заряда к массе вообще не зависит от длины цилиндра в отличие от макрочастиц сферической формы, где этот важный для ускорения параметр, характеризующий эффективность ускорения, линейно уменьшался с ростом диаметра макрочастиц. Само значение этого параметра велико, примерно такое же, как для сферической макрочастицы того же диаметра, что и диаметр цилиндра. При этом масса макрочастицы цилиндрической формы в сотни раз превышает массу макрочастицы сферической формы с диаметром, равным диаметру цилиндра.

2. Баллистика

Рассчитаем движение макрочастиц цилиндрической формы с острым конусом в головной части с учетом сопротивления воздуха. Уравнение движения макрочастиц можно записать в виде:

m d V / d t = − ρ C x S t r V 2 / 2,   ( 1 )

где m - масса макрочастицы, V - скорость, S_tr - площадь поперечного сечения макрочастицы, ρ = ρ 0 e − z / H 0 - барометрическая формула изменения плотности атмосферы с высотой, ρ₀=1.3*10^-3 g/cm³ - плотность воздуха у поверхности Земли, Н₀=7 km - значение высоты, на которой плотность падает в е раз.

Аэродинамическим коэффициентом или коэффициентом аэродинамического сопротивления называется безразмерная величина, учитывающая «качество» формы макрочастицы,

C x = F x / ( ½ ) ρ 0 V 0 2 S t r .   ( 2 )

Решение уравнения (1) может быть записано в виде:

V ( t ) = V 0 / [ 1 + ρ C x V 0 * S t r * t / 2 m ] .   ( 3 )

Для того, чтобы можно было вычислять изменение скорости макрочастиц со временем, необходимо найти аэродинамический коэффициент С_х.

3. Расчет коэффициента аэродинамического сопротивления

Будем считать, что макрочастица имеет форму цилиндрического стержня с конической головной частью. Тогда, при ударе молекулы азота по острому конусу, изменение продольной скорости молекул равно:

Δ V x = V x * Θ t 2 / 2,   ( 4 )

где Θ_t - угол конуса при вершине. Молекулы газа передают макрочастице импульс:

p = m V = ρ V x S t r * Δ V x .   ( 5 )

Изменение импульса в единицу времени - сила, сила лобового торможения,

F x 1 = ( ½ ) ρ V x S t r * V x * Θ t 2 .   ( 6 )

Разделив F_x1 на ( ½ ) ρ V x 2 S t r , получим коэффициент аэродинамического сопротивления для острого конуса при зеркальном отражении молекул от конуса, (формула Ньютона):

C x   a i r = Θ t 2 .   ( 7 )

Пусть длина конусной части макрочастицы равна: l_cone=1.3 cm при диаметре d_sh=2 mm. Это означает, что угол при вершине конуса равен: Θ_t=1.6*10^-1 и коэффициент аэродинамического сопротивления для острого конуса равен: С_х=2.5*10^-2.

Предложенный способ можно реализовать с помощью устройства

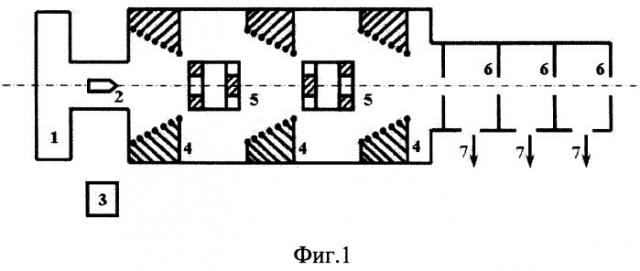
На Фиг.1 приведена схема устройства. Устройство состоит из пушки 1, где цилиндрические стержни 2 с конической головной частью разгоняют до начальной скорости V_in=I km/s. Стержни облучают пучком электронов из специального электронного ускорителя 3. Полем высоковольтного токового импульса с напряжением: U_acc=2 MV, распространяющегося по секциям 4 спирального волновода, с общей длиной L_acc=300 метров, цилиндрические стержни ускоряют до конечной скорости V_fin=6 km/s. Стержни фокусируют с помощью дублетов электростатических квадрупольных линз 5, расположенных между секциями, и выпускают в атмосферу через последовательность буферных объемов 6, имеющих индивидуальную откачку 7.

1. Выбор конечной скорости стержней

Соотношение между скоростью и энергией, приходящейся на нуклон, можно видеть из следующей таблицы.

Таблица 4
Зависимость между скоростью снаряда и энергией, приходящейся на нуклон
Vsh, km/s	1	2	3	4	5	6
ε, eV/nucl.	5*10-3	2*10-2	5*10-2	8*10-2	0.125	0.2

Видно, что конечной скорости макрочастицы, равной V_{sh fin}=6 km/s, соответствует энергия, приходящаяся на один нуклон в снаряде, порядка W_fin≈0.2 eV/nucleon.

2. Предварительное ускорение макрочастиц газодинамическим методом

Начальная, после порохового старта, скорость макрочастицы может быть оценена из следующих соображений. Тепловая скорость молекул сгоревшего пороха может быть определена из молекулярной массы продуктов горения М и температуры сгоревших продуктов Т:

β T = ( k T / М с 2 ) 1 / 2 ,   ( 8 )

где k=1.38*10^-16 erg/degree - постоянная Больцмана, lerg=6.24*10¹¹ eV, М=Nm_n, где m_n - масса нуклона, m_nc²=1 GeV, N - число нуклонов в молекулах продуктов горения, N=100, с=3*10¹⁰ cm/s, скорость света в вакууме, Т=10 degree. После подстановки численных значений в формулу (1), найдем, что тепловая скорость продуктов горения равна: β_T=3*10^-6. При этом реальная скорость снаряда будет равна: V_sh=1 km/s.

Для достижения этой скорости у снаряда вытянутой, стреловидной формы, может потребоваться откачка ствола пушки, то есть удаление газа из ствола при выстреле. Величина противодавления, давления, действующего со стороны воздуха, находящегося в стволе, на снаряд, может быть оценена из формулы:

P o p p = ρ V s h 2 / 2,   ( 9 )

где ρ - плотность сжатого воздуха в стволе пушки, ρ=3-4ρ₀, ρ₀=1.3*10^-3 g/cm³ - плотность воздуха при нормальных условиях. После подстановки численных значений в формулу (9) получим, что величина противодавления может составлять: Р_орр=2.5*10⁷ dn/cm²=25 atm. Таким образом, откачка ствола пушки может быть весьма полезна. В вакууме же должно производиться и электродинамическое доускорение снаряда, а выпуск его в атмосферу должен осуществляться через последовательность откачиваемых буферных объемов.

Возможно, впрочем, использование подкалиберного снаряда позволит достичь большей начальной скорости, чем мы предполагаем.

3. Ускорение макрочастиц в спиральном волноводе

Известно, [2], что в спиральном волноводе могут распространяться медленные электромагнитные волны, фазовая скорость которых может быть порядка скорости звука в воздухе. В таком волноводе можно ускорять электрически заряженные стержни с конической головной частью, для этого нужно, чтобы начальная скорость стержня и фазовая скорость волны приблизительно совпадали. По мере ускорения стержня фазовую скорость волны в спиральном волноводе нужно увеличивать так, чтобы стержень находился все время в одной и той же фазе волны, называемой синхронной. Увеличивать фазовую скорость волны в спиральном волноводе можно, увеличивая шаг намотки спирали [2].

Ускоряемый стержень должен содержать двигатель для коррекции орбиты при полете в воздухе, топливо для двигателя. Необходимо также иметь систему наведения стержня на космический мусор, стержень должен содержать систему навигации, системы управления, приемник и передатчик.

Диаметр стержня пусть будет равен: d_sh=2 mm, длина l_sh=300 mm.

Тогда площадь поперечного сечения стержня равна:

s_tr=πd_sh ²/4=3.14*10^-2 cm², объем стержня: V_sh≈1 cm³. Масса стержня, для случая средней плотности стержня ρ_aver=5 g/cm, равна: m_sh=5 g.

3.1. Отношение Z/А

Примем среднюю атомную массу стержня равной A_sh=30. Найдем число нуклонов в стержне из пропорции:

6*10²³ - 30 g

х - 5 g

откуда х=10²³ атомов или A_sh=3*10²⁴ нуклонов.

Примем поверхностную напряженность электрического поля на стержне равной: E_surf=3*10⁷ V/cm. Из формулы для поверхностной напряженности поля для цилиндра:

E s u r f = 2 κ / r ,   ( 10 )

найдем плотность заряда, приходящуюся на единицу длины стержня

κ = E s u r f * r / 2 e = ( 5 * 10 7 * 0.1 ) / ( 5 * 10 − 10 * 300 * 2 ) = 10 13 ,   ( 11 )

откуда можно найти:

N e = ( κ / e ) * l s h = 3 * 10 14 .   ( 12 )

Таким образом, если «посадить» на стержень N_e=3*10¹⁴ электронов, то поверхностная напряженность поля получится равной: E_surf=3*10⁷ V/cm.

Теперь, зная общее число избыточных электронов на стержне N_e=3*10¹⁴ и количество нуклонов в нем A_sh=3*10²⁴, можно найти отношение заряда к массе для стержня: Z/A=N_e/A=3*10¹⁴/3*10²⁴=10^-10.

3.2. Длина ускорения

Темп ускорения заряда в электрическом поле можно записать как:

Δ W = ( Z / A ) e E z w ,   ( 13 )

и для напряженности поля волны E_zw=70 kV/cm темп набора энергии составит: ΔW=7*10^-4 eV/(m*nucleon), так что требуемый прирост энергии Δε=0.2 eV/nucleon будет, достигнут на длине:

L a c c = Δ ε / Δ W = 300   m ,   ( 14 )

что является приемлемым для размещения ускорителя на корабле.

4. Облучение стержня пучком электронов

Для того чтобы ускорять в спиральном волноводе цилиндрический стержень с острым конусом в головной части, его надо электрически зарядить. Сообщить электрический заряд стержню можно, облучая его пучком электронов, таким образом, чтобы облучающие стержень электроны на нем оставались. Тогда электрический заряд стержня будет расти пропорционально току пучка электронов и длительности облучения. Пусть ток облучающего стержень электронного пучка равен: I_beam=5 А, а длительность импульса тока равна: τ_beam=10 µs. Тогда общее количество электронов в таком токовом импульсе как раз равно: N_e=I_beam*τ_beam/e=3*10¹⁴ электронов.

4.1. Облучение макрочастиц пучком электронов. Энергия электронов

Пусть на ускоренный газодинамическим способом до скорости V_in=1 km/s цилиндрический стержень попадает пучок электронов, полученный из внешнего источника. Будем исходить из поверхностной напряженности поля: E_surf=30 MV/cm. Тогда для диаметра цилиндра d_sh=2 mm получим, что минимальная энергия электронов, способных преодолеть кулоновское отталкивание ранее размещенных на макрочастице электронов, должна быть: W_e>eE_surf*d_sh/2=3 MeV.

4.2. Облучение макрочастиц пучком электронов. Длина пробега

Электроны с энергией 3 MeV имеют пробег в алюминии, примерно равный 1 g/cm², [5], стр.957. Принимая плотность алюминия равной: ρ_A1=2.7 g/cm³, найдем, что экстраполированный пробег электронов в алюминии равен: l_A1≈4 mm. Поскольку средняя плотность вещества, выбранная нами для цилиндра, ρ_aver.=5 g/cm³, примерно вдвое превышает плотность алюминия, то длина пробега электронов с энергией 3 MeV в стержне будет примерно равна: 2 mm.

По-видимому, надо плавно увеличивать энергию электронов в процессе облучения. Надо, чтобы по мере «размещения» электронов на стержне электроны, испущенные позже, с одной стороны имели достаточно большую энергию, чтобы преодолеть кулоновское расталкивание уже находящихся на стержне электронов, с другой стороны, энергия электронов не должна быть слишком большой - надо, чтобы пробег электронов в веществе стержня был много меньше его диаметра.

В этом диапазоне энергий пробег электронов в веществе линейно возрастает с энергией и, например, электроны с энергий W_e=300 keV, имеют пробег 0.2 mm и не смогут пересечь диаметр макрочастицы 2 mm. Они будут терять свою энергию на ионизацию вещества и будут останавливаться в толще макрочастицы.

4.3. Облучение макрочастиц пучком электронов. Автоэлектронная эмиссия

«Посадить» несколько зарядов на макрочастицу - не составит проблемы, но дальше, когда электронов на макрочастице будет много, они начнут стекать с нее за счет автоэлектронной эмиссии. Пусть напряженность поля для автоэлектронной эмиссии составляет: E_surf=3*10⁷ V/cm. После того, как посажено достаточно много электронов, для того, чтобы посадить последующие, надо преодолеть отталкивание тех, которые уже там сидят. И это значит, что энергия электронов, которые мы хотим посадить на макрочастицу, должна быть достаточно большой, такой, чтобы они могли преодолеть этот кулоновский барьер, долететь до макрочастицы и на ней остаться.

«Посадить» большой электрический заряд будет мешать автоэлектронная эмиссия. Часть заряда за счет туннельного эффекта будет непрерывно утекать с макрочастицы.

4.4. Покрытие цилиндра платиной и пассивирование кислородом

Чтобы создать поверхностный барьер для электронов, «разместившихся» на макрочастице, нужно возможно больше увеличить работу выхода для электронов из макрочастицы. Наибольшей известной работой выхода обладает платина, пассивированная кислородом, еφ=6.56 eV, [5], стр.445. Размещенный на макрочастице заряд будет с нее стекать путем автоэлектронной эмиссии в соответствии с формулой, [5], стр.444.

j = e 2 E 2 / ( 8 π h ϕ ) * exp { [ − ( 8 π / 3 ) ( 2 m ) 1 / 2 / h ] * [ ( e ϕ ) 3 / 2 / ( e E ) * θ ( y ) ] } ,   ( 15 )

где θ(y) - функция Нордгейма, в которой аргументом является относительное снижение работы выхода внешним электрическим полем по Шоттки.

4.5. Утечка электронов

Найдем количество электронов, которые покинут макрочастицу, за время ускорения. Для напряженности поля: Е=30 MV/cm и работы выхода: еφ=6.5 eV из графика, [5], стр.461, найдем, что плотность тока утечки равна: j=10^-9 A/cm².

Утечка заряда ΔQ будет равна:

Δ Q = j * S s u r f * t a c c ,   ( 16 )

где j=10^-9 A/cm² - ток утечки, S_surf≈20 cm² - площадь боковой поверхности макрочастицы.

Время ускорения может быть определено из соотношения:

t a c c = L a c c / V a v e r ,   ( 17 )

где L_acc=300 m - длина ускорения, V_aver=3 km/s - средняя скорость на длине ускорения. Вычисленное по формуле (17) время ускорения получается равным: t_acc=0.1 s.

Подставляя цифры в формулу (16), найдем, что ΔN_e=10 электронов и это составляет 3*10^-5 от числа электронов, посаженных на макрочастицу.

5. Выбор параметров спирального волновода

Начальная скорость снаряда в спирали β_{sh in}, выраженная в единицах скорости света β_in=V_in/с, где с=3*10¹⁰ cm/s, скорость света в вакууме, равна: β_in=3.3*10^-6, конечная: β_fin=2*10^-5. Спираль, по-видимому, должна будет состоять из нескольких секций, так, что в пределах каждой секции можно выбирать оптимальную частоту ускорения. Длина волны ускорения может быть определена из условия: х=2πr₀/(β*λ₀)=1, где x - безразмерный параметр, входящий в аргументы модифицированных функций Бесселя, r₀ - радиус спирали, β - фазовая скорость волны, λ₀ - длина волны ускорения в вакууме, λ₀=c/f₀, f₀ - частота ускорения.

Выбирая начальный радиус спирали r_{0 in} равным: r_{0 in}=20 cm, ε=1280 - диэлектрическая проницаемость среды, расположенной в области между спиралью и экраном, найдем: λ₀=3.8*10⁷ cm, f₀=790 Hz. Таким образом, замедленная длина волны для начала ускорения равна: λ_slow=βλ₀=1.25 m.

5.2. Параметры спирали

Для того чтобы получить требуемую напряженность поля волны Е₀ в спиральном волноводе, в него требуется ввести мощность, определяемую по формуле. [2],

P = ( c / 8 ) * E 0 2 * r 0 2 * β * { } ,   ( 18 )

где Р - вводимая в спиральный волновод высокочастотная мощность, r₀ - радиус спирали, β - фазовая скорость волны, определяемая из дисперсионного уравнения. Фигурная скобка в формуле (18) равна:

{ } = { ( 1 + I 0 K 1 / I 1 K 0 ) ( I 1 2 − I 0 I 2 ) + ε ( I 0 / K 0 ) 2 ( 1 + I 1 K 0 / I 0 K 1 ) ( K 0 K 2 − K 1 2 ) } ,   ( 19 )

где I₀, I₁, I₂ - модифицированные функции Бесселя первого рода,

К₀, K₁, К₂ - модифицированные функции Бесселя второго рода. Первое слагаемое в фигурной скобке соответствует потоку, распространяющемуся внутри спирали, первое слагаемое соответствует потоку, распространяющемуся вне спирали. Поскольку пространство между спиралью и экраном заполнено диэлектриком, то перед вторым слагаемым появился сомножитель ε, [2].

В нашем случае для замедлений электромагнитной волны до скоростей порядка скорости звука требуется использование как геометрических свойств структуры (спираль с мелким шагом), так и свойств среды, нами выбрано значение относительной диэлектрической проницаемости ε=1280.

Таким образом, поток высокочастотной мощности, распространяющийся вне спирали, более чем в 10 раз превосходит мощность, распространяющуюся внутри спирали. Поэтому первым слагаемым внутри фигурной скобки можно пренебречь по сравнению со вторым, само значение фигурной скобки для аргумента х=1 приблизительно равно: {}≈4ε.

В ускорителях синхронную фазу выбирают на переднем склоне импульса, так что ускоряющее частицу электрическое поле всегда меньше амплитудного значения. Выберем синхронную фазу равной: φ_s=45°, sinφ_s=0.7, E_zw=E₀sinφ_s. Таким образом, амплитудное значение волны, которой будет ускоряться цилиндрический стержень, должно быть равно:

E 0 = E z w / sin ϕ s = 100   k V / c m .   ( 20 )

Тогда мощность волны, выраженная по формуле (18) в Ваттах, равна:

P ( W ) = 3 * 10 10 * 10 10 * 4 * 10 2 * 3.3 * 10 − 6 * 1.28 * 10 3 * 4 / ( 8 * 9 * 10 4 10 7 ) ≈ 300   M W .   ( 21 )

5.2. Переход от синусоидальной волны к одиночному импульсу

Такая мощность может быть достижима для импульсной техники. Разложим синусоидальный импульс, [2], соответствующий полуволне E_pulse=E_0puisesin(2π/T₀)t, 2π/Т₀=ω₀, ω₀=2πf₀ в ряд Фурье.

f 1 ( ω ) = ( 2 / π ) 1 / 2 ∫ sin ω 0 t 0 T 0 / 2 * sin ω t d t .   ( 22 )

Спектр импульса достаточно узкий и занимает область частот от 0 до 2ω₀. Поскольку в спиральном волноводе дисперсия (зависимость фазовой скорости от частоты) слабая, можно ожидать, что весь спектр частот от 0 до 2ω₀ будет распространяться примерно с одной и той же фазовой скоростью. В результате полуволновой синусоидальный импульс в пространстве будет расплываться в 3.5 раза только за счет увеличения фазовой скорости волны. Согласование спирального волновода с подводящим фидером в этом случае надо осуществлять в полосе частот: Δf≈ω₀/2π.

Введем понятие амплитуды импульса U, связанное с напряженностью поля на оси спирали Е₀ соотношением, [2]:

U ˜ p u l s e = E 0 p u l s e λ s l o w / 2 π ,   λ s l o w β λ 0 ,   λ 0 = c / f 0 .   ( 23 )

Выбор длины волны λ₀=3.8*10⁷ cm означает, что мы выбрали длительность ускоряющего магнитного диполя импульса равной: (f₀=с/λ₀=790 Hz), τ_pulse=1/(2f₀)=630 µs. Амплитуда напряжения импульса будет равна: U ˜ p u l s e = E 0 p u l s e λ s l o w / 2 π = 2   M V , а импульсный ток, текущий по виткам спирали, будет равен: I ˜ = P / U ˜ = 150   A . В Таблице 5 собраны основные параметры ускорителя.

Таблица 5

Параметры ускорителя

Z/A=10-1010, диэл