Способ определения коэффициента пропитки обмоток электрических машин

Способ определения коэффициента пропитки обмоток электрических машин

Иллюстрации

Показать все

Реферат

Изобретение относится к электротехнике, а именно к способу определения коэффициента пропитки обмоток электрических машин, соединенных в звезду с изолированной нейтралью.

Известен способ контроля качества пропитки обмоток электрических машин, предложенный в работе [2], который заключается в измерении емкости обмотки относительно магнитного сердечника до пропитки Сдп и емкости относительно магнитного сердечника после пропитки и сушки обмотки Спп, а о качестве пропитки предложено судить по коэффициенту пропитки Кпр, определяемому из выражения

К п р = С п п С д п                                         ( 1 )

Недостатком способа-аналога является низкая точность контроля, так как величины Сдп и Спп зависят от расположения витков в обмотке, а также от того как распределился состав по корпусным полостям обмотки. При попадании одинакового количества (массы) пропиточного состав в две разные однотипные обмотки одной партии Кпр, определяемый по формуле (1), может давать существенно отличающиеся друг от друга значения. Поэтому формула (1) не позволяет объективно судить о насыщенности полостей обмотки пропиточным составом.

Наиболее близким к заявляемому способу является способ определения коэффициента пропитки обмоток, описанный в работе [2], частично устраняющий указанные выше недостатки аналога.

В способе-прототипе [2], по которому у каждой обмотки из данной партии измеряют емкости относительно корпуса до пропитки и после пропитки и сушки, одну из обмоток, произвольно выбранную из данной партии, после измерения емкости относительно корпуса до пропитки погружают в пропиточную жидкость с известной диэлектрической проницаемостью обмотки и измеряют емкость относительно корпуса, не вынимая обмотку из пропиточной жидкости, а коэффициент пропитки для каждой из оставшихся обмоток данной партии определяют по формуле

К п р = 1 ln ε 2 ln ε 1 С п п ( С п п * С д п * − 1 ) С п п * С д п * С д п ( ε 1 − 1 ) − С п п ( ε 1 − С п п * С д п * )                                   ( 2 )

где С_дп, С_пп - емкости обмотки относительно корпуса соответственно до пропитки и после пропитки и сушки; С д п * - емкость произвольно выбранной обмотки относительно корпуса до пропитки; С п п * - емкость произвольно выбранной обмотки относительно корпуса после выдержки в пропиточной жидкости с известной диэлектрической проницаемостью до полного заполнения ею полостей обмотки; ε₁ - диэлектрическая проницаемость пропиточной жидкости; ε₂ - диэлектрическая проницаемость отвержденного пропиточного состава.

Недостатком способа-прототипа является необходимость у одной из произвольно выбранных обмоток измерять емкость относительно корпуса до пропитки, затем, после измерения емкости относительно корпуса до пропитки, погружать упомянутую обмотку в пропиточную жидкость с известной диэлектрической проницаемостью, и измерять емкость обмотки относительно корпуса, не вынимая обмотку из пропиточной жидкости. Введение этой операции усложняет способ.

Кроме того, по способу-прототипу определяют усредненный коэффициент пропитки обмоток, но этим способом невозможно определить распределенность пропиточного состава по фазам обмотки, которая в большинстве электрических машин соединена в звезду с изолированной нейтралью, что снижает информативность и точность контроля качества пропитки.

Технической задачей, на которую направлено изобретение, является упрощение способа, повышение его информативности и точности.

Поставленная техническая задача решается тем, что в способе определения коэффициента пропитки обмоток электрических машин, характеризующем степень заполнения пропиточным составом полостей обмотки, при котором у каждой обмотки из данной партии измеряют электрические параметры до пропитки и после пропитки и сушки, в качестве электрических параметров выбирают емкости двух фаз обмотки, соединенной в звезду, которые поочередно измеряют до пропитки С_дп12, С_дп13, С_дп23 и после нее С_пп12, С_пп13, С_пп23 относительно корпуса, после чего по результатам измерений определяют коэффициент пропитки каждых двух фаз К_пр12, К_пр13, К_пр23 по формулам

К п р 12 = 1 ln ε п с × ln С п п 12 ( С э к в − С д п 12 ) С д п 12 ( С э к в − С п п 12 ) ,                                     ( 3 )

К п р 13 = 1 ln ε п с × ln С п п 13 ( С э к в − С д п 13 ) С д п 13 ( С э к в − С п п 13 ) ,                                       ( 4 )

К п р 23 = 1 ln ε п с × ln С п п 23 ( С э к в − С д п 23 ) С д п 23 ( С э к в − С п п 23 ) ,                                        ( 5 )

где С э к в = 2 p S ε 0 ε э ε к 3 ( d э ε к + d к ε э )        ( 6 ) - эквивалентная емкость последовательно соединенных емкостей эмали и корпусной изоляции двух фаз обмотки, p - количество пазов в магнитном сердечнике; S - площадь паза; ε₀=8,854187·10^-12 - электрическая постоянная; ε_э - диэлектрическая проницаемость эмалевой пленки провода обмотки; ε_к - диэлектрическая проницаемость корпусной изоляции; d_э - толщина эмалевой изоляции провода; d_к - толщина корпусной изоляции провода. После чего определяют коэффициенты пропитки каждой фазы обмотки по формулам

К п р 1 = К п р 12 − К п р 23 + К п р 13 ,       ( 7 )

К п р 2 = К п р 23 − К п р 13 + К п р 12 ,         ( 8 )

К п р 3 = К п р 13 − К п р 12 + К п р 23 ,       ( 9 )

где K_пр1, K_пр2, К_пр3 - коэффициенты пропитки 1-й, 2-й, 3-й фаз соответственно.

На фиг 1. схематически представлена обмотка трехфазной электрической машины, соединенная звездой с изолированной нейтралью. Позициями 1, 2, 3 обозначены выводы фаз обмотки, позицией 4 обозначена нейтраль обмотки.

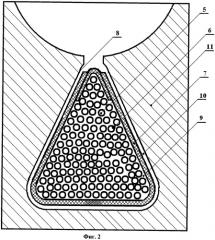
На фиг.2 представлено сечение обмотки в одном из пазов, представляющее слоистую систему.

Она состоит из проводов обмотки 5, покрытых слоем эмали 6, корпусной изоляции 7, поверхности паза 8, воздушных полостей между поверхностью обмотки и корпусной изоляцией 9 и воздушных полостей между корпусной изоляцией и поверхностью паза 10, магнитного сердечника (корпус) 11.

На фиг.3 изображены емкости обмотки относительно корпуса, которым является магнитный сердечник статора электрической машины, представлены в виде слоистого плоского конденсатора до пропитки (фиг.3,А) и после нее (фиг.3,Б). На фиг.3,А и фиг.3,Б введены те же обозначения, только на фиг.3,Б вместо позиций 9 и 10 введены позиции 12 и 13, так как воздушные полости обмотки 9 и 10 после пропитки и сушки частично заполняются пропиточным составом. В связи с этим позициями 12 и 13 обозначены те же слои 9 и 10, но заполненные статистически распределенными по этим слоям частицами пропиточного состава. Фиг.1, фиг.2 и фиг.3 служат для пояснения сущности изобретения.

Сущность способа заключается в следующем.

Обмотки трехфазных электрических машин обычно соединяют звездой (см. фиг.1).

В способе-прототипе выводы фаз 1, 2, 3 соединяют между собой и до пропитки измеряют емкость обмотки Сдп относительно магнитного сердечника. После пропитки и сушки обмотки вновь соединяют выводы 1, 2, 3 между собой и измеряют емкость обмотки Спп. Затем по формуле (2), используя результаты всех измерений, описанных в способе-прототипе, определяют интегральный усредненный коэффициент пропитки обмотки. Между тем качество пропитки оценивается не только этим усредненным интегральным коэффициентом пропитки, но и тем, насколько равномерно распределился пропиточный состав по полостям обмотки.

Обмотка электрической машины, размещенная в пазы магнитного сердечника, представляет собой слоистую систему (см. фиг.1). Так как толщина d_э эмалевой изоляции 6 провода 5, толщина d_к корпусной изоляции 7, и суммарная толщина d_в воздушных полостей между поверхностью обмотки и корпусной изоляцией 9 и воздушных полостей между корпусной изоляцией и поверхностью паза 10 пренебрежительно малы и составляют несколько микрон, то емкость обмотки относительно корпуса можно с пренебрежительно малой погрешностью представить в виде слоистого плоского конденсатора (см. фиг.3). Если до пропитки соединить между собой выводы фаз 1 и 2 (фиг.1) и измерить емкость этих двух фаз относительно магнитного сердечника до пропитки С_дп12, а затем повторить эту же процедуру с выводами 1-3 и 2-3 и измерить до пропитки емкости двух соответствующих фаз С_дп13 и С_дп23, то эти емкости, поскольку они соединены последовательно, можно записать, в соответствии с фиг.2, в виде следующих соотношений:

1 С д п 12 = 1 С э 12 + 1 С к 12 + 1 С в 12 ,            ( 10 )

1 С д п 13 = 1 С э 13 + 1 С к 13 + 1 С в 13 ,               ( 13 )

1 С д п 23 = 1 С э 23 + 1 С к 23 + 1 С в 23 ,             ( 12 )

где С_э12, С_э13, С_э23 - емкости слоя эмаль-изоляции у двух фаз 1-2, 1-3, 2-3 соответственно, С_к12, С_к13, С_к23 - емкости слоя корпусной изоляции у двух фаз 1-2, 1-3, 2-3 соответственно, С_в12, С_в13, С_в23 - суммарные емкости воздушных слоев 9 и 10 (фиг.3) у двух фаз 1-2, 1-3, 2-3 соответственно.

Так как у однотипных обмоток количество пазов, в которых расположены две фазы обмотки, площадь паза, толщина d_э эмалевой и толщина корпусной d_к изоляции одинаковые, то следует принять, что С_э12=С_э13=С_э23=С_э(13) и С_к12=С_к13=С_к23=Ск (14).

Учитывая соотношения (13) и (14), выражения (10), (11) и (12) можно переписать в виде

1 С д п 12 = 1 С э + 1 С к + 1 С в 12 ,                   ( 15 )

1 С д п 13 = 1 С э + 1 С к + 1 С в 13 ,                      ( 16 )

1 С д п 23 = 1 С э + 1 С к + 1 С в 23                                               ( 17 )

Для плоского конденсатора можно записать

С э = 2 3 р × ε 0 ε э S d э                                ( 18 )

С к = 2 3 р × ε 0 ε к S d к                                  ( 19 )

С в 12 = 2 3 р × ε 0 ε в S d в 12                                 ( 20 )

С в 13 = 2 3 р × ε 0 ε в S d в 13                                  ( 21 )

С в 23 = 2 3 р × ε 0 ε в S d в 23                               ( 22 )

где р - количество пазов в магнитном сердечнике статора, ε_э, ε_к, ε_в - диэлектрические проницаемости эмали, корпусной изоляции, воздуха соответственно, ε₀=8,854187817·10^-12 - электрическая постоянная; С_в12, С_в13, С_в23 - суммарные емкости воздушных слоев 9 и 10 (фиг.2) двух фаз 1-2, 1-3, 2-3 соответственно. Подставив выражения (18), (19), (20), (21), (22) в формулы (15), (16), (17) и учитывая, что диэлектрическая проницаемость воздуха ε_в=1, можно записать

1 С д п 12 = 3 d э 2 р ε э ε 0 S + 3 d к 2 р ε 0 ε к S + 3 d 12 2 р ε 0 S ,                                    ( 23 )

1 С д п 13 = 3 d э 2 р ε 0 ε э S + 3 d к 2 р ε 0 ε к S + 3 d 13 2 р ε 0 S ,                                     ( 24 )

1 С д п 23 = 3 d э 2 р ε 0 ε э S + 3 d к 2 р ε 0 ε к S + 3 d 23 2 ε 0 р S ,                                     ( 25 )

Из выражений (23), (24) и (25) следует

d 12 = 2 3 р S ε 0 ( 1 С д п 12 − 3 d э 2 р ε 0 ε э S − 3 d к 2 р ε 0 ε к S ) = = 2 3 ε 0 р S С д п 12 − d э ε э − d к ε к = 2 р S ε 0 ε э ε к − 3 С д п 12 ( d э ε к + d к ε э ) 3 ε э ε к С д п 12 ,              ( 26 )

d 13 = 2 р S ε 0 ε э ε к − 3 С д п 13 ( d э ε к + d к ε э ) 3 ε э ε к С д п 13                ( 27 )

d 23 = 2 р S ε 0 ε э ε к − 3 С д п 23 ( d э ε к + d к ε э ) 3 ε э ε к С д п 23                  ( 28 )

После пропитки и сушки обмоток объемы полостей 12 и 13 частично заполняются пропиточным составом, имеющим диэлектрическую проницаемость ε_п (см. фиг.3,Б). Так как пропиточный состав не полностью заполняет объемы полостей 12 и 13, а статистически распределен по полостям 12 и 13, то в упомянутых полостях образуется бинарная статистическая смесь, состоящая из частиц пропиточного состава и частиц воздуха, с диэлектрической проницаемостью ε*. Диэлектрическая проницаемость бинарной смеси ε* подчиняется распределению Лихтенеккера-Ротера [3], в соответствии с которым можно записать для фаз 1-2 в виде

ln ε 12 * = V п 12 V 12 ln ε п + V 12 − V п 12 V 12 ln ε в           ( 29 )

где V_п12 - объем, который занимают частицы пропиточного состава в слоях 11 и 12,

V₁₂-V_п12 - объем воздуха в слоях 12 и 13, ε₁₂* - диэлектрическая проницаемость статистической смеси в слоях 12 и 13 фаз 1-2.

Учитывая, что диэлектрическая проницаемость воздуха ε_в=1, a lnε_в=0, выражение (29) можно записать в виде

ln ε 12 * = V п 12 V 12 ln ε п = = К п р 12 ln ε п                 ( 30 )

В выражении (30) отношение V п 12 V 12 есть не что иное, как коэффициент пропитки K_пр12 объемов полостей фаз 1-2, характеризующий степень заполнения объема полостей V₁₂ пропиточным составом.

Аналогичные выражения можно записать для слоев 12 и 13 (фиг.3,Б) для фаз 1-3 и 2-3

ln ε 13 * = V п 13 V 13 ln ε п = К п р 13 ln ε п                    ( 31 )

ln ε 23 * = V п 23 V 23 ln ε п = К п р 23 ln ε п                    ( 32 )

Если после пропитки и сушки измерить емкости C_пп12, C_пп13, С_пп23 двух соответствующих фаз относительно корпуса и учесть, что пропиточный состав, диэлектрическая проницаемость которого ε_п, статистически распределился по объемам зазоров d₁₂, d₁₃, d₂₃, то емкости слоев 12 и 13 в соответствующих двух фазах можно представить выражениями

С п 12 = 2 3 р × ε 0 ε * 12 S d в 12                                         ( 33 )

С п 13 = 2 3 р × ε 0 ε * 13 S d в 13                              ( 34 )

С п 23 = 2 3 р × ε 0 ε * 23 S d в 23                            ( 35 )

Подставив в уравнения (15), (16) и (17) вместо С_в12, С_в13, С_в23 величины C_п12, C_п13, С_п23, можно записать выражения для емкостей C_пп12, C_пп13, С_пп23

1 С п п 12 = 3 d э 2 р ε 0 ε э S + 3 d к 2 р ε 0 ε к S + 3 d 12 2 р ε 0 ε * 12 S ,             ( 36 )

1 С п п 13 = 3 d э 2 р ε 0 ε э S + 3 d к 2 р ε 0 ε к S + 3 d 13 2 р ε 0 ε * 13 S ,              ( 37 )

1 С п п 23 = 3 d э 2 р ε 0 ε э S + 3 d к 2 р ε 0 ε к S + 3 d 23 2 р ε 0 ε * 23 S ,                ( 38 )

Из соотношений (36), (37), (38) выразим зазоры d₁₂, d₁₃, d₂₃

d 12 = 2 3 р ε 0 ε * 12 S ( 1 С п п 12 − 3 d э 2 р ε 0 ε э S − 3 d к 2 р ε 0 ε к S ) = ε 0 ε * 12 ( 2 3 р S С п п 12 − d э ε 0 ε э − d к ε 0 ε к ) = = ε * 12 [ 2 р S ε 0 ε э ε к − 3 С п п 12 ( d э ε к + d к ε э ) 3 ε э ε к С п п 12 ] ,               ( 39 )

d 13 = ε * 12 [ 2 р S ε 0 ε э ε к − 3 С п п 13 ( d э ε к + d к ε э ) 3 ε э ε к С п п 13 ]               ( 40 )

d 23 = ε * 12 [ 2 р S ε 0 ε э ε к − 3 С п п 23 ( d э ε к + d к ε э ) 3 ε э ε к С п п 23 ]             ( 41 )

Так как после пропитки и сушки зазоры d₁₂, d₁₃, d₂₃ в контролируемой обмотке не изменились, то можно приравнять правые части выражений (26), (27), (28) к правым частям соответствующих выражений (39), (40), (41), получим

ε * 12 [ 2 р S ε 0 ε э ε к − 3 С п п 12 ( d э ε к + d к ε э ) 3 ε э ε к С п п 12 ] = 2 р S ε 0 ε э ε к − 3 С д п 12 ( d э ε к + d к ε э ) 3 ε э ε к С д п 12       ( 42 )

ε * 12 [ 2 р S ε 0 ε э ε к − 3 С п п 13 ( d э ε к + d к ε э ) 3 ε э ε к С п п 13 ] = 2 р S ε 0 ε э ε к − 3 С д п 13 ( d э ε к + d к ε э ) 3 ε э ε к С д п 13            ( 43 )

ε * 12 [ 2 р S ε 0 ε э ε к − 3 С п п 23 ( d э ε к + d к ε э ) 3 ε э ε к С п п 23 ] = 2 р S ε 0 ε э ε к − 3 С д п 23 ( d э ε к + d к ε э ) 3 ε э ε к С д п 23          ( 44 )

Из соотношений (42), (43), (44) выразим ε 12 * , ε 13 * , ε 23 * и, преобразовав полученные выражения, запишем

ε 12 * = С п п 12 ( С э к в − С д п 12 ) С д п 12 ( С э к в − С д п 12 )                                   ( 45 )

ε 13 * = С п п 13 ( С э к в − С д п