Способ определения концентрации билирубина

Способ определения концентрации билирубина

Иллюстрации

Показать все

Реферат

Изобретение относится к области лабораторного медицинского анализа, аналитического приборостроения.

В настоящее время большую часть измерений концентрации билирубина выполняют либо биохимическими методами [1], либо методами прямого фотометрирования плазмы крови, получаемой в лабораторных центрифугах с гематокритными капиллярами [2]. Оба метода не являются оперативными, требуют строгого выполнения длительных операций и высокой квалификации медперсонала. Кроме того, взятие пробы шприцем связано с травмированнием новорожденного и риском его инфицирования.

Неинвазивную оценку уровня билирубина можно получить при помощи транскутантных билирубинометров, основанных на явлении диффузии билирубина из крови в окружающую ткань (дерму). Транскутантные билирубинометры измеряют интенсивность отраженного от кожи света на нескольких длинах волн. Так, известно устройство для определения содержания билирубина в подкожных тканях и крови пациентов [3], использующее две длины волны - 492 и 523 нм. Первая из них находится на склоне спектральной кривой поглощения билирубина. Выбор второй обусловлен отсутствием поглощения на ней света билирубином и одновременно наличием примерно такого же, как на длине волны 492 нм, поглощения гемоглобином. Это позволяет исключить влияние капиллярных подкожных сосудов на результаты измерений. Для уменьшения влияния пигментации кожи в [3] используются разностные сигналы, образованные вычитанием двух сигналов рассеянного света с разной длиной оптического пути, содержащих одинаковые вклады меланина и других факторов тонкого верхнего слоя, и неодинаковые вклады билирубина и гемоглобина в толстом нижнем слое. Однако помимо меланина и кровеносных сосудов в коже содержится множество других факторов, влияющих на поглощение света. В частности, на точность транскутантных измерений билирубина с использованием [3] могут оказывать влияние объемный коэффициент рассеяния кожи, диаметр кровеносных сосудов, насыщение гемоглобина кислородом, а также контакт прибора с кожей (с некоторым нажимом). Все эти факторы являются причиной того, что при одинаковом содержании билирубина в крови двух пациентов билирубинометр [3] может показывать совершенно разный результат. Кроме того, билирубинометр [3] выдает результат в условных единицах, которые требуется переводить в клинические единицы на основе регрессионного анализа популяций возрастных групп.

Наиболее близким к предлагаемому является способ транскутанных измерений билирубина у новорожденных [4], использующий измерения диффузного отражения кожного покрова в более чем 100 точках из диапазона 350-800 нм и алгоритм коррекции факторов, связанных с пигментацией и зрелостью кожи (образование коллагена в эпидермисе и дерме). Результаты измерений не зависят от расовой принадлежности и возраста и выводятся в клинических единицах измерений (мг/дл или мкмоль/л). К недостаткам следует отнести невысокую точность расчета переноса излучения при решении обратной задачи, необходимость использования дорогостоящей спектрометрической аппаратуры и необходимость калибровки прибора перед каждым измерением, что еще больше увеличивает стоимость прибора.

Предлагаемое изобретение направлено на решение задачи повышения точности определения абсолютной концентрации билирубина за счет исключения влияния индивидуальных вариаций параметров кожи и контакта с ней прибора, устранения калибровочных измерений, а также упрощения процедуры измерений и снижения стоимости способа.

Для решения данной задачи в способе измерения концентрации билирубина путем посылки оптического излучения на кожу, измерения спектральной интенсивности рассеяного кожей излучения посылку излучения на кожу в одну или более точек осуществляют на длинах волн, характеристических для поглощения билирубина, окси- и деоксигемоглобина, измеряют интенсивность рассеянного излучения на одном или нескольких расстояниях от точек посылки излучения, а количественные значения концентрации билирубина определяют из аналитических выражений, связывающих ее с измеряемыми коэффициентами диффузного рассеяния. Характеристическими длинами волн являются области максимума поглощения билирубина 460 нм, оксигемоглобина 576 нм, изобестические точки производных гемоглобина 500 или 529 нм, и длины волн, соответствующие максимальному различию коэффициентов поглощения окси- и деоксигемоглобина 660 и 840 нм. При этом: 1) интенсивность рассеянного излучения на длинах волн 460, 500, 576, 660 и 840 нм измеряют на одном расстоянии L от точки посылки излучения, а концентрацию билирубина определяют из аналитического выражения, связывающего ее со спектральными значениями коэффициента диффузного рассеяния R(L,λ)=P(L,λ)/(P₀(λ)A(L,λ)), где P₀(λ) - мощность посылаемого излучения, A(L,λ) - аппаратурная константа; 2) интенсивность рассеянного излучения на длинах волн 460, 500, 576 и 840 им измеряют не менее чем на двух расстояниях меду точками посылки излучения, а концентрацию билирубина определяют из аналитического выражения, связывающего ее с отношениями r_n(λ)=R(L_n,λ)/R(L₁,λ), где R(L_n,λ)=P(L_n,λ)/(P₀(λ)A(L_n,λ)), P(L_n,λ) - мощности регистрируемых сигналов диффузного рассеяния, L_n - расстояния между точками посылки и регистрации излучения, n≤N_L - количество точек регистрации диффузного рассеяния, A(L_n,λ) - аппаратурные константы; 3) интенсивность рассеянного излучения на длинах волн 460, 500 и 660 нм измеряют не менее чем на трех расстояниях между точками посылки излучения, а концентрацию билирубина определяют из аналитического выражения, связывающего ее с отношениями r_n(λ).

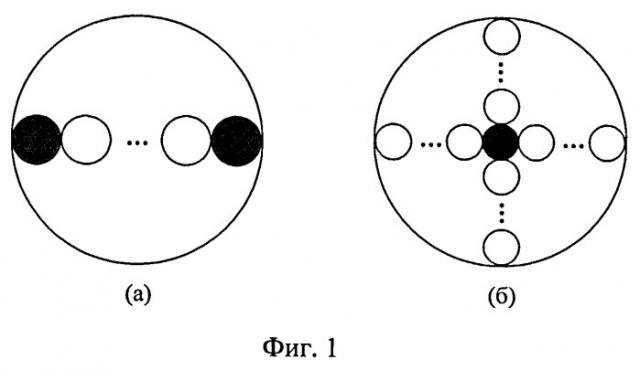
Сущность данного изобретения поясняется с помощью фиг.1-3. На фиг.1 представлены геометрические схемы приемно-излучающей части (оптоволоконного зонда) измерителя концентрации билирубина, где закрашенный кружок - источник излучения (световод), светлые кружки - приемники излучения (световоды), большой круг - оболочка оптоволоконного зонда, включающего приемные и излучающий световоды. В одном из вариантов (фиг.1, а) оптоволоконный зонд для измерений диффузного рассеяния содержит два источника излучения, между которыми вплотную размещаются N_L приемников излучения. Излучение от лазерных диодов последовательно подается в излучающие световоды. Рассеянное тканью в заднее полупространство излучение попадает в принимающие световоды, через которые оно поступает на фотоприемники. Сравнение профилей рассеянного излучения от симметрично расположенных каналов возбуждения позволяет оценить степень неоднородности освещаемого объема и тем самым выбирать оптимальный для проведения измерений участок кожи. В качестве альтернативы может использоваться такая конфигурация оптических волокон (фиг.1, б), при которой в центре зонда находится излучающий световод, а по нескольким направлениям от него симметрично размещаются принимающие световоды. Такая схема также позволяет выявлять неоднородность исследуемого участка кожи и, кроме того, позволяет увеличить уровень полезного сигнала на фоне шума за счет большей суммарной собирательной способности принимающих световодов.

С точки зрения оперативности и автоматизации мониторинга концентрации билирубина C_bil в тканях дермы новорожденных представляет интерес возможность ее прямого расчета через измеряемые коэффициенты диффузного рассеяния R(L,λ). Детерминированной функциональной зависимости между C_bil и R(L,λ) не существует, однако статистическая зависимость (множественная регрессия) может быть получена на основе ансамбля реализации C_bil и R(L,λ). Для этого осуществляются измерения R(L,λ) для образцов биоткани или моделирующих ее фантомов с известными значениями C_bil. Другой подход к получению вышеотмеченного ансамбля - это расчет R(L,λ) методом Монте-Карло для математической модели кожи с варьирующимися параметрами [5]. Ниже рассматривается именно этот вариант.

К настоящему времени известно огромное количество публикаций, посвященных моделированию распространения света в биологических тканях и расчету их коэффициентов диффузного рассеяния (КДР). Кожа в большинстве случаев моделируется как плоскопараллельная, горизонтально однородная среда, включающая три слоя - роговой, эпидермис и дерма. Причем роговой слой, в силу малой оптической толщины, играет крайне незначительную роль в отражении света кожей, и его условно включают в состав эпидермального слоя. В связи с этим математическая модель кожи, используемая в настоящей работе, описывает ее структуру в виде двух плоских слоев, принципиально отличающихся по составу и оптическим свойствам. Верхний слой - эпидермис с толщиной L_epi=50-130 мкм, нижний - дерма, которая в оптическом плане считается бесконечно толстой. Показатель преломления слоев кожи n_skin относительно воздуха считается одинаковым, поэтому френелевское отражение излучения имеет место только на границе раздела кожи с внешней средой.

Известно, что основными параметрами, характеризующими распространение оптического излучения в рассеивающей среде, являются коэффициенты поглощения k и рассеяния β, а также индикатриса рассеяния или ее средний косинус g. Причем в оптике биологических тканей, как очень мутных сред, для описания световых полей достаточно знать не сами величины β и g, а их комбинацию - редуцированный коэффициент рассеяния µ_s=β(1-g).

Полагаем, что основой кожи является слабопоглощающая, обескровленная ткань. Зависимость ее коэффициента поглощения k_t [см^-1] от длины волны λ [нм] аппроксимируется следующим выражением:

k t ( λ ) = 0.244 + 85.3 ⋅ exp ( − ( λ − 154 ) / 66.2 ) .           ( 1 )

В качестве индикатрисы рассеяния "эффективных" рассеивателей ткани (основными из которых являются упакованные в жгуты коллагеновые и эластиновые волокна дермы, а также кератиноциты и меланоциты эпидермиса) используем функцию Хеньи-Гринштейна, спектральная зависимость фактора анизотропии (среднего косинуса) которой может быть описана эмпирическим соотношением:

g ( λ ) = 0.7645 + 0.2355 ⋅ [ 1 − exp ( − ( λ − 500 ) / 729.1 ) ] .       ( 2 )

Спектр редуцированного коэффициента рассеяния µ_s(λ) биологических тканей в видимой и ближней ИК-областях спектра рассчитывается как суперпозиция спектров µ_s(λ), соответствующих рассеивателям Ми и Рэлея с размерами d≥λ и d<<λ соответственно:

μ s ( λ ) = μ s ( λ 0 ) [ ρ M i e ( λ 0 λ ) x + ( 1 − ρ M i e ) ( λ 0 λ ) 4 ] ,             ( 3 )

где λ₀=400 нм; ρ_Mie - доля рассеяния Ми; x - параметр спектральной зависимости редуцированного коэффициента рассеяния Ми, зависящий от размера рассеивателей и их показателя преломления.

Объемные коэффициенты поглощения слоев кожи определяются по известным правилам сложения оптических величин как сумма коэффициентов поглощения отдельных компонент кожи с весами, равными объемным концентрациям компонент. Спектр коэффициента поглощения эпидермиса рассчитывается в соответствии с объемными концентрациями меланина f_mel и воды w_epi в его составе:

k e p i ( λ ) = f m e l k m e l ( λ ) + w e p i k w ( λ ) + ( 1 − f m e l ) k t ( λ ) ,           ( 4 )

где k_mel и k_w - коэффициенты поглощения меланина и воды.

Коэффициент поглощения дермы зависит от содержания в ней капилляров с кровью f_blood, воды w_derm и билирубина C_bil:

k d e r m ( λ ) = f b l o o d α k b l o o d ( λ ) + w d e r m k w ( λ ) + + ( 1 − f b l o o d ) ( k t ( λ ) + ln ( 10 ) C b i l μ b i l ε b i l ( λ ) ) ,                   ( 5 )

где ε_bil - молярный коэффициент поглощения билирубина в см^-1/(моль/литр); µ_bil=585 г/моль - молярная масса билирубина; k_blood - коэффициент поглощения крови; α - корректирующий фактор, учитывающий эффект локализованного поглощения света кровеносными сосудами. Для расчета α использовалось аналитическое выражение для хаотически распределенных капилляров с диаметром D:

α = 2 3 1 − exp [ − π k b l o o d D ( 1 − 0.043 k b l o o d D ) / 2 3 ] π k b l o o d D .           ( 6 )

Коэффициент поглощения крови k_blood в зависимости от длины волны излучения может быть представлен в виде суммы коэффициентов поглощения гемоглобина (окисленного и неокисленного) и билирубина:

k b l o o d ( λ ) = ln ( 10 ) C H b μ H b [ S ⋅ ε H b ( λ ) + ( 1 − S ) ⋅ ε H b O 2 ( λ ) ] + + ln ( 10 ) t d i f C b i l μ b i l ε b i l ( λ ) ,                                 ( 7 )

где C_Hb [г/литр] - концентрации общего гемоглобина в крови; µ_Hb=64500 г/моль - молярная масса гемоглобина; ε H b O 2 и ε_Hb - молярные коэффициенты поглощения окcи- и деоксигемоглобина в см^-1(моль/литр); S - насыщение крови кислородом (доля окисленного гемоглобина в общем гемоглобине); t_dif=5 - отношение концентраций билирубина в крови и в окружающей ткани (полагается фиксированным).

Таким образом, оптическая модель кожи определяется следующими параметрами: показатель преломления цельной кожи - n_skin, параметры спектральной зависимости редуцированного коэффициента рассеяния - µ_s(λ₀), ρ_Mie и x; толщина эпидермиса L_epi; объемные концентрации меланина и воды в эпидермисе - f_mel и w_epi; объемные концентрации капилляров с кровью, воды и билирубина в дерме - f_blood, w_derm и C_bil; средний диаметр капилляров - D; концентрация общего гемоглобина в крови - C_tHb; насыщение крови кислородом - S. Диапазоны вариаций модельных параметров, выбранные путем критического анализа результатов различных авторов, приведены в табл.1. Следует отметить, что для учета возможного увеличения объемного коэффициента рассеяния кожи за счет контакта с ней измерителя, верхняя граница диапазона вариаций параметра µ_s(λ₀) выбрана примерно в полтора раза выше максимального значения µ_s(λ₀), наблюдаемого в экспериментах.

Табл. 1
Диапазоны вариаций параметров оптической модели кожи
Параметр	Диапазон
nskin	1.4-1.5
µs(λ0), см-1	50-150
ρMie	0.1-0.6
x	0.5-1.0
µs(λ)/µs (900 нм)	3-10
fmel, %	0.5-25
Lepi, мкм	50-130
fmel·Lepi, мкм	0.6-15
wepi, %	27-33
wderm, %	60-77
fblood, %	0.2-2
Cbil, мг/литр	5-250
CtHb, г/литр	100-225
S, %	40-99
D, мкм	5-30

Для моделирования распространения оптического излучения в коже человека используется метод Монте-Карло, основанный на прослеживании случайных блужданий большого количества фотонов (конкретно использовалось 3·10⁶ фотонов) от точки их влета в среду до их поглощения или вылета из среды [6]. После статистического моделирования траекторий всех фотонов рассчитывается функция поверхностного распределения коэффициента направленного рассеяния:

S ( r , μ ) = π I ( r , μ ) F ,

где I - интенсивность излучения, выходящего из элементарной площадки на расстоянии r от начала координат в телесном угле ΔΩ=2πµΔµ, описанном вокруг направления µ=cosθ; F - поток излучения, падающего на среду в точке r=0 в направлении нормали к ее поверхности.

Для канала регистрации, расположенного на расстоянии L от канала возбуждения, измеряемой величиной является коэффициент диффузного рассеяния R(L,λ), который с точностью до аппаратурной константы A(L,λ) представляет собой отношение мощности регистрируемого сигнала к мощности зондирующего светового пучка:

R ( L , λ ) = A ( L , λ ) 4 π r 0 2 ∫ μ c 1 2 μ d μ ∫ − r 0 r 0 l ⋅ arccos ( l 2 + ( l + x ) 2 − r 0 2 2 l ( l + x ) ) d x ×           × ∫ l − r l S ( λ , y , μ ) ⋅ arccos ( y 2 + l 2 − r 2 2 l y ) d y

где r₀ и r - соответственно радиусы передающего и принимающего световодов; l=L-x, L - расстояние между световодами; μ c = 1 − A c 2 , А_с - числовая апертура оптического волокна; x и y - переменные интегрирования.

Расчет R(L,λ) осуществлялся по следующей схеме. Случайным образом выбирались значения модельных параметров из диапазонов их вариаций, приведенных в табл.1. Если полученные значения параметров удовлетворяют соответствующим ограничениям, то производился расчет µ_s(λ), k_epi(λ) и k_derm(λ) по формулам (1)-(7), в противном случае осуществлялось повторное разыгрывание параметров. Для каждой реализации оптических параметров методом Монте-Карло вычислялись коэффициенты R(L,λ), соответствующие схемам оптоволоконных измерений диффузного рассеяния, приведенным фиг.1, при следующих значениях параметров: λ=460, 500, 529, 560, 576, 660, 760, 805, 840, 940 нм, L₁=0.43 мм, L₂=1.06 мм, диаметр сердцевины излучающего волокна 200 мкм, принимающих - 600 мкм, толщина оболочки всех волокон 15 мкм, числовая апертура А_с=1.0. Длина волны 460 нм соответствует максимуму спектральной кривой поглощения билирубина; 500, 529, 805 нм - изобестические точки производных гемоглобина (в которой поглощение кровью зависит только от концентрации общего гемоглобина); 560, 576, 660, 840 нм - соответствует максимальному различию молярных коэффициентов поглощения гемоглобина и оксигемоглобина; 760 нм - локальный максимум коэффициента поглощения деоксигемоглобина, 940 нм - попадает в полосу поглощения воды.

Очевидно, что для определения C_bil не обязательно использовать все десять вышеуказанных длин волн, поскольку некоторые из спектральных значений КДР кожи являются линейно зависимыми и их использование при решении обратной задачи не приведет к улучшению точности восстановления C_bil. Для выбора оптимального количества длин волн оптического зондирования необходимо проанализировать степень взаимозависимости спектральных значений R(λ)=R(L₂,λ) на фиксированном расстоянии L₂=1.06 мм от точки освещения. Такой анализ может быть выполнен на основе рассмотрения собственных чисел ковариационной матрицы

S i j = 1 σ i σ j ∑ k = 1 K ( R k ( λ i ) − R ( λ i ) ¯ ) ( R k ( λ j ) − R ( λ j ) ¯ ) ,

где R^k(λ) - реализация спектра КДР, K=10³ - количество таких реализации, R ( λ ) ¯ - усредненный спектр КДР, 1≤i,j≤10. Каждое из собственных чисел l_i (i=1,…,20) матрицы S определяет относительный вклад соответствующего собственного вектора в вариации R(λ), возникающие при изменении структурных и биохимических параметров кожи. Число независимых компонент определяется номером собственного числа, для которого l_i>δR², где δR - погрешность измерений КДР. Оказалось, что при δR=5% вариации R(λ) содержат пять независимых компонент (l₅≈0.005). Такой результат является вполне понятным, если учесть, что спектральные особенности КДР кожного покрова обусловлены влиянием пяти основных факторов - присутствием в составе кожи меланина, крови и билирубина, а также коэффициентом рассеяния кожи и его относительным спектральным ходом.

Выбор оптимальных значений λ₁, …, λ₅ производился путем компьютерного перебора всех возможных комбинаций из 10 вышеуказанных λ и оценки погрешностей восстановления C_bil из соответствующих спектральных значений R(λ) с использованием полиномиальной регрессии следующего вида

ln C b i l = a 00 + ∑ n = 1 N λ ∑ m = 1 M a n m [ ln R ( λ n ) ] m ,                            ( 8 )

где N_λ=5, М=3 - степень полинома, a _nm - коэффициенты, численные значения которых рассчитываются методом наименьших квадратов на основе ансамбля реализации C_bil и R(λ). Использование в (8) логарифмов позволяет достичь одинаковой погрешности аппроксимации статистической связи между C_bil и R(λ) во всем диапазоне их значений и устраняет возможность получения отрицательных значений C_bil. Коэффициенты a _nm регрессии (8) между C_bil и R(λ_n) при λ₁=460 нм, λ₂=500 нм, λ₃=576 нм, λ₄=660 нм и λ₅=840 нм приведены в табл.2.

Оценка погрешности восстановления C_bil с использованием регрессии (8) оценивалась на основе замкнутых численных экспериментов, суть которых состоит в следующем. При каждой реализации R(λ) осуществляется расчет C_bil с использованием (8) при наложении на R(λ) случайных отклонений в пределах δR=5% (моделирующих погрешности измерений). Полученное в результате значение C b i l * сравнивается со значением C_bil, соответствующим рассматриваемой реализации, и рассчитывается погрешность восстановления C_bil. После перебора всех реализациЙ вычисляется средняя погрешность δC_bil, под которой в дальнейшем и будем понимать погрешность восстановления C_bil.

Таблица 2
Коэффициенты a nm регрессии (8) между Cbil и R(λn) при λ1=460 нм, λ2=500 нм, λ3=576 нм, λ4=660 нм и λ5=840 нм.
N	m
0	1	2	3
0	-260.42
1		-5.1688	-0.3205	-0.0079
2	14.999	1.3894	0.0458
3	-5.0141	-0.5023	-0.0151
4	-18.887	-2.7962	-0.1334
	-142.56	-29.185	-1.9911

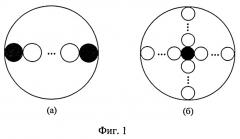
На основании вышеизложенного анализа выбраны следующие длин волн: λ₁=460 нм; λ₂=500 нм; λ₃=576 нм; λ₄=660 нм; λ₅=840 нм. На фиг.2 (а, б) приведены результаты восстановления C_bil из значений КДР на данных λ при погрешностях δR=0 и 5%, а также указаны средние погрешности восстановления C_bil. Погрешность δC_bil, соответствующая δR=0%, является предельно достижимой погрешностью восстановления концентрации билирубина с использованием вышеуказанного набора длин волн оптического зондирования. Данная погрешность обусловлена общей вариативностью биофизических параметров кожного покрова (коэффициента рассеяния, концентрации меланина и крови, диаметра капилляров с кровью, насыщения крови кислородом) и может быть уменьшена только при наличии априорной информации или с использованием дополнительных λ. Однако, как было отмечено выше, при δR=5% для восстановления C_bil не имеет смысла использовать более пяти λ, поскольку соответствующие им значения R(λ) линейно зависимы. Следует отметить, что теоретически чувствительность измерений R(λ) к концентрации билирубина можно увеличить с увеличением расстояния между каналами возбуждения и регистрации. Этот факт является очевидным, поскольку для определения C_bil необходимо, чтобы изменение интенсивности излучения за счет поглощения билирубином на оптическом пути от источника к приемнику превышало погрешность регистрации КДР. Однако проведение измерений R(λ) при больших расстояниях между каналами возбуждения и регистрации сопряжено с рядом сложностей, связанных с низким уровнем полезного сигнала и влиянием на результат интерпретации R(λ) горизонтальной неоднородности кожи.

Регрессии (8), соответствующие вышеуказанным значениям λ_i, …, λ₅, составляют основу способа неинвазивного определения уровня билирубина в крови у новорожденных, использующего измерение диффузного рассеяния на одном фиксированном расстоянии от точки освещения в пяти спектральных участках. Однако, устройство, реализующее вышеописанный способ, требует калибровки, поскольку коэффициенты R(L,λ) определяются из измеряемых сигналов диффузного рассеяния P(L,λ)=P₀(λ)R(L,λ)G(L,λ)τ(λ)S(λ), скорректированных с учетом мощности посылаемого излучения P₀(λ), спектральной чувствительности приемника S(λ), функции пропускания оптической системы τ(λ) и собирательной способности оптических волокон G(L,λ).

Устранить необходимость калибровки измерений P(L,λ) можно, если определять концентрацию билирубина из отношений КДР для двух и более пространственно разнесенных каналов регистрации. В этом случае для перехода от измеряемых сигналов к отношениям r(λ)=R[L₂,λ)/R(L₁,λ) необходимо располагать информацией только о параметре G(L,λ), влияние которого, при известных апертурах принимающих волокон, несложно учесть в расчетах R(L,λ). Кроме того, угловое распределение рассеянного излучения для рассматриваемых каналов регистрации является практически одинаковым, поэтому, при равенстве апертур принимающих волокон, отношение G(L₁,λ)/G(L₂,λ) мало отличается от единицы.

Вследствие малого различия оптических толщин, проходимых светом в тонком слое эпидермиса, на пути от источника до ближнего и дальнего каналов регистрации отношение r(λ) практически не зависит от пигментации кожи. Это обстоятельство является причиной того, что при погрешности δR=5% количество независимых компонент в спектрах r(λ) на единицу меньше, чем в спектрах R(L,λ). Следовательно, при использовании двух пространственных каналов регистрации диффузного рассеяния для восстановления C_bil достаточно четырех спектральных измерений r(λ). Результаты замкнутых численных экспериментов по восстановлению C_bil с использованием регрессии аналогичных (8), с заменой R(λ_n) на r(λ_n) и N_λ=4, позволяют заключить, что наименьшие погрешности δC_bil соответствуют длинам волн 460, 500, 576 и 840 нм. На фиг.2 (в, г) приведены соответствующие результаты восстановления С_bil для всего смоделированного ансамбля реализации C_bil и r(λ). Восстановление C_bil производилось при наложении на r(λ) случайных отклонений δr=0 и 5%. Видно, что с использованием регрессионного подхода к решению обратной задачи можно определять концентрацию билирубина во всем диапазоне ее возможных значений. Разброс точек на рисунках относительно прямой C b i l * = C b i l характеризует чувствительность решения обратной задачи к погрешности оптических измерений, а также к вариациям биофизических параметров кожи и контакту с ней оптоволоконного зонда (напомним, что при получении ансамбля реализации C_bil и R(L,λ) редуцированный коэффициент рассеяния кожи µ_s(λ₀) варьировался в диапазоне, верхняя граница которого более чем в полтора раза превышает наибольшее значение µ_s(λ₀) для кожи человека). Такие результаты восстановления C_bil являются приемлемыми для удовлетворения практических потребностей и сравнимы с погрешностями биохимических методов контроля желтухи у новорожденных. Коэффициенты a _nm регрессии (8) между C_bil и r(λ_n) при λ₁=460 нм, λ₂=500 нм, λ₃=576 нм и λ₄=840 нм приведены в табл.3.

Таблица 3
Коэффициенты a nm регрессии (8) между Cbil и r(λn) при λ1=460 нм, λ2=500 нм, λ3=576 нм и λ4=840 нм
N	m
0	1	2	3
0	5.3633
1		-6.5273	-0.7025	-0.0286
2	16.875	3.0912	0.1982
3	-5.5641	-1.3331	-0.1055
4	0.3078	0.4642	0.1092

Сравнивая результаты, представленные на фиг.2 (а, б) и фиг.2 (в, г), можно сделать вывод, что информативность восстановления C_bil (как отношение априорной неопределенности к апостериорной) для двухканальных измерений R(L,λ) выше, чем для одноканальных. При этом использование для восстановления C_bil коэффициентов r(λ) позволяет исключить влияние нестабильности оптико-электронного тракта и погрешностей калибровки на результат определения билирубина.

Таким образом, бескалибровочный метод измерения абсолютной концентрации билирубина в дерме по пункту 4) формулы изобретения включает измерение сигналов диффузного рассеяния P(L,λ) на двух расстояниях от центра освещаемого участка кожи (рис.1) в спектральных участках λ=460, 500, 576 и 840 нм, вычисление для каждой λ коэффициентов r(λ)=P(L₂,λ)/P(L₁,λ) и определение концентрации билирубина с использованием аналитического выражения (множественной регрессии), связывающего искомый параметр с r(λ). При этом исключается влияние факторов, связанных содержанием меланина и гемоглобина в тканях кожи, рассеивающими свойствами кожи и контактом с ней оптоволоконного зонда. Повышается точность измерений за счет исключения калибровочных измерений.

Известно, что измерения диффузного рассеяния на нескольких расстояниях от точки освещения позволяют разделить вклады рассеяния и поглощения в регистрируемые сигналы. Если для решения обратной задачи использовать нормированные сигналы диффузного рассеяния r_n(λ)=R(L_n,λ)/R(L₂,λ), то для исключения влияния рассеивающих свойств кожи на результат восстановления ее коэффициента поглощения k(λ) необходимо осуществлять измерение r_n(λ) не менее чем на трех расстояниях от излучающего световода. Значения k(λ), определяемые на основе отношений сигналов диффузного рассеяния для рядом расположенных каналов регистрации, не зависят также и от пигментации кожи, поскольку оптические пути, проходимые светом в тонком слое эпидермиса, для них примерно одинаковы. Таким образом, при определении билирубина в максимуме его поглощения λ=460 нм необходимо учесть только присутствие окси- HbO₂ и деоксигемоглобина Hb. Это достигается с использованием длин волн 500 и 660 нм. Первая длина волны является изобестической, так как поглощение оптического излучения Hb и HbO₂ одинаково и соответствующий ей коэффициент поглощения k (500 нм) пропорционален концентрации общего гемоглобина. Вторая длина волны характеризуется высоким поглощением света Hb и низким поглощением HbO₂, что обуславливает высокую чувствительность коэффициента k (660 нм) к концентрации Hb.

Рассмотрим оценки точности восстановлени