Устройство для формирования траектории перевода судна на параллельный курс с соблюдением ограничений на диапазон изменения сигнала управления

Устройство для формирования траектории перевода судна на параллельный курс с соблюдением ограничений на диапазон изменения сигнала управления

Иллюстрации

Показать все

Реферат

Изобретение относится к области судовождения, в частности к системам автоматического управления движением судна.

Современные авторулевые позволяют управлять движением судна по траекториям, имеющим различную форму. Траектория, по которой должно перемещаться судно, называется исполнительной траекторией и она используется авторулевым как задающий сигнал. Исполнительные траектории могут быть ломаными линиями, сплайновыми кривыми и т.п. Однако, для минимизации бокового отклонения судна от исполнительной траектории, необходимо учитывать физические ограничения, связанные с динамическими параметрами судна. Траектории должны быть как минимум С² - гладкими функциями на отрезке, т.к. в реальном мире вектор скорости тела не может изменяться мгновенно. Дополнительно, существуют ограничения на диапазон изменения сигнала управления, зависящие от скорости движения судна.

В источнике [1] рассматривается вопрос применения полиномов третьей степени для задания исполнительных траекторий. Однако использование полиномов третьей степени при построении исполнительных траекторий не обеспечивает непрерывность второй производной, кривизны траектории и, следовательно, физическую реализуемость этой траектории, возможные ограничения на диапазон изменения сигнала управления не учитываются.

Наиболее близким к изобретению является устройство для автоматического вывода судна на заданную прямолинейную траекторию прохождения узкого участка фарватера и удержания его на этой траектории, которое содержит автоматический регулятор путевого угла, датчики координат центра масс судна, путевого угла, угловой скорости поворота судна в горизонтальной плоскости, продольной скорости судна, угла перекладки руля, выходы которых соединены соответственно с первым, вторым, третьим, четвертым и пятым входами автоматического регулятора путевого угла, снабженного вычислителем заданных параметров и бокового отклонения с тремя входами, первый вход которого образует одноименный вход автоматического регулятора путевого угла, и вычислителем сигнала управления с шестью входами, второй, третий, четвертый и пятый входы которого образуют одноименные входы автоматического регулятора путевого угла, первый вход которого образован выходом вычислителя заданных параметров движения и бокового отклонения, а выход упомянутого автоматического регулятора, образованный выходом вычислителя сигнала управления, подключен к рулевому приводу, механически связанному с рулем, который механически соединен с датчиком угла перекладки руля и корпусом судна, с которым механически связаны датчики координат центра масс судна, путевого угла, угловой скорости поворота судна в горизонтальной плоскости, продольной скорости судна, блок расчета теоретической траектории перехода из начальной точки на заданную прямолинейную траекторию прохождения узкого участка фарватера с шестью входами и тремя выходами и блок постоянной памяти с тремя выходами, в который записаны параметры заданной траектории прохождения узкого участка фарватера, минимальный радиус кривизны траектории движения судна, коэффициенты закона управления, первый выход которого соединен с шестым входом упомянутого автоматического регулятора, а второй и третий выходы блока постоянной памяти подключены к пятому и шестому входам упомянутого блока расчета теоретической траектории, первый, второй, третий и четвертый входы которого соединены соответственно с выходами датчиков координат центра масс судна, путевого угла, угловой скорости поворота судна в горизонтальной плоскости и продольной скорости, первый и второй выходы упомянутого блока расчета теоретической траектории подключены соответственно к седьмому и восьмому входом автоматического регулятора путевого угла, а третий выход упомянутого блока расчета теоретической траектории служит для формирования сигнала судоводителю (патент RU 2406645 C1, G01C 21/14, опубликован 14.08.2009).

В известном устройстве критерием допустимости сформированной траектории является минимальный радиус кривизны этой траектории. Однако для сформированной допустимой траектории не выполняется проверка необходимого диапазона отклонения рулевого органа. Длины направляющих векторов в граничных точках траектории перевода судна из начальной точки на заданную прямолинейную траекторию являются результатом решения экстремальной задачи, которая должна быть решена во время работы указанного устройства, что увеличивает время подготовки маневра.

Техническим результатом является повышение безопасности перевода судна на параллельный курс.

Указанный технический результат достигается тем, что устройство для формирования траектории перевода судна на параллельный курс содержит задатчик абсолютной величины максимально допустимого сигнала управления, датчик продольной скорости, вычислитель критических параметров траектории перевода судна на параллельный курс с двумя входами и двумя выходами, задатчик расстояния смещения параллельного курса от текущего курса, вычислитель изменения путевого угла Δϕ, минимального радиуса R_m первого допустимого оптимального полиноминального отрезка (ДОЭПО) и длины L прямого отрезка между двумя ДОЭПО с четырьмя входами и двумя выходами, датчик координат центра масс судна, вычислитель набора параметров граничных точек первого ДОЭПО с четырьмя входами и одним выходом, датчик путевого угла, вычислитель выходных параметров элементарных отрезков, составляющих траекторию перевода судна на параллельный курс, с двумя входами и одним выходом, первый вход вычислителя критических параметров траектории перевода судна на параллельный курс соединен с выходом задатчика абсолютной величины максимально допустимого сигнала управления, второй вход вычислителя критических параметров траектории перевода судна на параллельный курс соединен с выходом датчика продольной скорости, первый и второй выходы вычислителя критических параметров траектории перевода судна на параллельный курс соединены со вторым и третьим входами, соответственно, вычислителя изменения путевого угла Δϕ, минимального радиуса R_m первого ДОЭПО и длины L прямого отрезка между двумя ДОЭПО, первый вход вычислителя изменения путевого угла Δϕ, минимального радиуса R_m первого ДОЭПО и длины L прямого отрезка между двумя ДОЭПО соединен с выходом задатчика расстояния смещения параллельного курса от текущего курса, четвертый вход вычислителя изменения путевого угла Δϕ, минимального радиуса R_m первого ДОЭПО и длины L прямого отрезка между двумя ДОЭПО соединен с выходом датчика продольной скорости, первый выход вычислителя изменения путевого угла Δϕ, минимального радиуса R_m первого ДОЭПО и длины L прямого отрезка между двумя ДОЭПО соединен со вторым входом вычислителя набора параметров граничных точек первого ДОЭПО, второй выход вычислителя изменения путевого угла Δϕ, минимального радиуса R_m первого ДОЭПО и длины L прямого отрезка между двумя ДОЭПО соединен со вторым входом вычислителя выходных параметров элементарных отрезков, составляющих траекторию перевода суд на параллельный курс, первый вход вычислителя набора параметров граничных точек первого ДОЭПО соединен с выходом задатчика расстояния смещения параллельного курса от текущего курса, третий вход вычислителя набора параметров граничных точек первого ДОЭПО соединен с выходом датчика координат центра масс судна, четвертый вход вычислителя набора параметров граничных точек первого ДОЭПО соединен с выходом датчика путевого угла, выход вычислителя набора параметров граничных точек первого ДОЭПО соединен с первым входом вычислителя выходных параметров элементарных отрезков, составляющих траекторию перевода судна на параллельный курс, на выходе вычислителя выходных параметров элементарных отрезков формируется траектория перевода судна на параллельный курс, состоящая из первого ДОЭПО и второго ДОЭПО или состоящая из трех элементарных отрезков: первого ДОЭПО, прямого отрезка и второго ДОЭПО (первый и второй ДОЭПО симметричны), которая используется авторулевым как исполнительная траектория в процессе управления движением судна при переводе судна на параллельный курс.

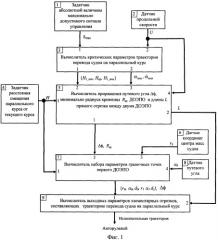
На фиг.1 представлена структурно-функциональная схема устройства для формирования траектории перевода судна на новый курс с соблюдением ограничений на диапазон изменения сигнала управления.

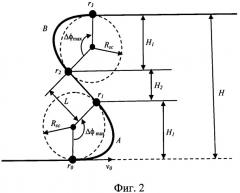
На фиг.2 - траектория перевода судна на параллельный курс, состоящая из трех отрезков: криволинейного r₀Ar₁ (первый ДОЭПО), прямого отрезка r₁r₂ и криволинейного r₂Br₃ (второй ДОЭПО).

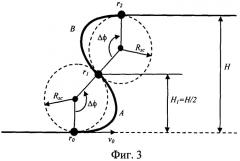
На фиг.3 - траектория перехода на параллельную траекторию, состоящую из двух криволинейных отрезков r₀Ar₁ (первый ДОЭПО) и r₁Br₂ (второй ДОЭПО).

На фиг.4 - основные параметры криволинейного отрезка траектории.

На фиг.5 - элементарный полиномиальный отрезок r₀Ar₁, обеспечивающий изменение путевого угла на Δϕ, где R_sc - радиус задающей окружности отрезка r₀Ar₁, R_m - минимальный радиус кривизны отрезка r₀Ar₁.

На фиг.6 - график функции r_sc(Δϕ).

На фиг.7 - вычисление координат граничной точки r₁ ОЭПО (ОЭПО частный случай ДОЭПО) r₀Ar₁ .

На фиг.8 - график сервисной функции d₁(Δϕ).

На фиг.9 - График функции ƒ_cl(Δϕ).

На фиг.10 - График функции h_c(λ_c).

На фиг.11 - График функции h_b(λ_b).

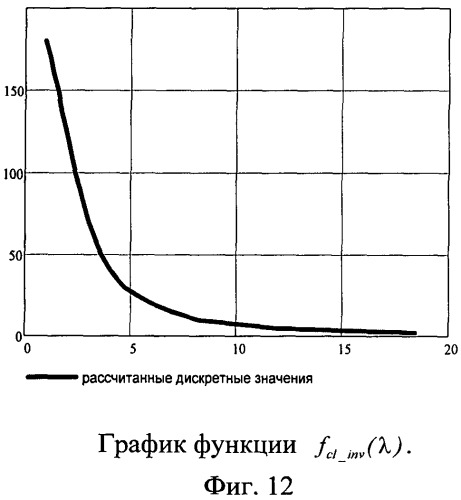
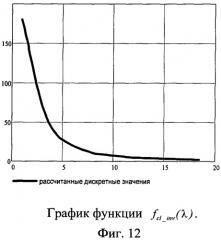
На фиг.12 - График функции f_cl__jnv(λ).

Устройство для формирования траектории перевода судна на параллельный курс с соблюдением ограничений на диапазон изменения сигнала управления содержит задатчик 1 (фиг.1) абсолютной величины максимально допустимого сигнала управления, датчик 2 продольной скорости, вычислитель 3 критических параметров траектории перевода судна на параллельный курс с двумя входами и двумя выходами, задатчик 4 расстояния смещения параллельного курса от текущего курса, вычислитель 5 приращения путевого угла Δϕ, минимального радиуса кривизны R_m первого ДОЭПО, и длины L прямого отрезка между двумя ДОЭПО, с четырьмя входами и двумя выходами, датчик 6 координат центра масс судна, вычислитель 7 набора параметров граничных точек первого ДОЭПО с четырьмя входами и одним выходом, датчик 8 путевого угла, вычислитель 9 выходных параметров элементарных отрезков, составляющих траекторию перевода судна на параллельный курс, с двумя входами и одним выходом.

Выход задатчика 1 связан с первым входом вычислителя 3, выход датчика 2 связан с вторым входом вычислителя 3 и четвертым входом вычислителя 5. Первый выход вычислителя 3 связан с вторым входом вычислителя 5, второй выход вычислителя 3 связан с третьим входом вычислителя 5, выход задатчика 4 связан с первым входом вычислителя 5 и первым входом вычислителя 7. Первый выход вычислителя 5 связан с вторым входом вычислителя 7, второй выход вычислителя 5 связан с вторым входом вычислителя 9. Выход датчика 6 связан с третьим входом вычислителя 7, выход датчика 8 связан с четвертым входом вычислителя 7. Выход вычислителя 7 связан с первым входом вычислителя 9. Выход вычислителя 9 связан с входом авторулевого или с судоводителем, использующего траекторию перехода на параллельный курс в качестве исполнительной траектории.

Траектория перехода на параллельный курс обязательно должна содержать участок схода с текущей траектории и участок выхода на параллельную траекторию. На фиг.2 показан общий случай траектории перевода судна на параллельный курс.

Введем следующие обозначения.

v 0 = [ v 0 x v 0 y ] - вектор скорости судна в начале траектории перехода на параллельный курс (см. фиг.2 и 3),

U|v₀| - абсолютная величина путевой скорости судна,

δmax - предельная величина перекладки руля при абсолютной величине продольной скорости судна U,

ω . =F(δ,ω) - дифференциальное уравнение модели продольного движения судна,

где ω - угловая скорость поворота корпуса судна в горизонтальной плоскости,

δ - угол перекладки руля.

r 0 = [ x 0 y 0 ] - декартовы координаты начала траектории перехода на параллельный курс (фиг.2 и 3),

Δϕ - величина приращения путевого угла при движении по криволинейному отрезку (фиг.2 и 3),

Δϕ_min, Δϕ_max - предельные величины изменения путевого угла при построении траекторий перевода судна на параллельный курс (фиг.2),

Н - расстояние смещения параллельного курса от текущего курса. Н>0 - смещение вправо по отношению к направлению исходной траектории. H<0 - смещение влево по отношению к направлению исходной траектории (фиг.2, 3).

H₁ - высота криволинейного отрезка (фиг.2 и 3),

H₂ - высота прямого отрезка между двумя ДОЭПО (фиг.2),

L - длина прямого отрезка между двумя ДОЭПО (фиг.2).

Будут рассматриваться два вида траекторий перевода судна на параллельный курс: траектория, состоящая из трех отрезков: криволинейного r₀Ar₁, прямого отрезка r₁r₂ и криволинейного r₂Br₃ (фиг.2), и траектория, состоящая из двух криволинейных отрезков без прямой вставки (фиг.3),

где r₀, r₁ - координаты начальной и конечной точек отрезка r₀Ar₁, соответственно,

α₀, α₁ - направления касательных в начальной и конечной точках отрезка r₀Ar₁, соответственно.

В то же время параметры α₀, α₁ являются путевыми углами судна в начальной и конечной точках отрезка r₀Ar₁, соответственно, и курсами судна на прямых участках траектории, примыкающих к траектории r₀Ar₁.

Полиномиальную кривую пятой степени в базисе Бернштейна [2] P₅(u), у которых кривизна в начальной и конечной точках равна нулю, назовем элементарным полиномиальным отрезком (ЭПО).

P 5 ( u ) = A 0 B 0 5 ( u ) + A 1 B 1 5 ( u ) + A 2 B 2 5 ( u ) + A 3 B 3 5 ( u ) + A 4 B 4 5 ( u ) + A 5 B 5 5   u ∈ [ 0 ,1 ]    , (1 .2 .1) где А₀, А₁, А₂, A₃, А₄, A₅ - двумерные коэффициенты,

B i 5 ( u ) - базисные полиномы Бернштейна пятой степени, которые обладают повышенной вычислительной устойчивостью,

u - скалярный параметр, принимающий значения в диапазоне от 0 до 1.

В качестве криволинейных отрезков будем применять элементарные полиноминальные отрезки.

Для траектории, состоящей из ЭПО и прямых отрезков, равенство нулю кривизны в граничных точках ЭПО обеспечивает физически реализуемый (безударный) переход судна с одного отрезка траектории на другой.

Будем считать, что абсолютная величина путевой скорости U постоянна при движении судна вдоль траектории.

Задачу построения ЭПО будем рассматривать в декартовой системе координат, у которой ось X направлена на восток, а ось Y - на север. ЭПО однозначно определяется набором параметров граничных точек [2].

{r₀, α₀, d₀, с₀, r₁, α₁, d₁,с₁},

где r₀, r₁ - координаты начальной и конечной точек ЭПО, соответственно,

α₀, α₁ - направления касательных в начальной и конечной точках ЭПО, соответственно,

d₀, d₁ - длины касательных в начальной и конечной точках ЭПО, соответственно,

c₀, c₁ - кривизна в начальной и конечной точках ЭПО, соответственно,

Величина α₀ измеряется навигационной системой судна. Значения следующих параметров выводятся из условий задачи

α 1 = α 0 + Δ φ ,             с 0 = 0,     c 1 = 0 (1.2.2)

где α₀,α₁ - направления касательных в начальной и конечной точках ЭПО, соответственно. c₀, c₁ - кривизна в начальной и конечной точках ЭПО, соответственно.

Δϕ - приращение путевого угла,

[ v 0 x v 0 y ] - вектор скорости судна в начале траектории перехода на новый курс.

Из [2] следует, что умножение каждого коэффициента А₀, А₁, А₂, A₃, А₄, A₅ на число k≠0 приводит к умножению на k параметров r₀, r₁, d₀, d₁ и делению на k кривизны во всех точках полиномиальной кривой.

Задача построения ЭПО состоит в том, чтобы найти значения d₀, r₁, d₁, которые задают такую траекторию, что при управлении движением судна по этой траектории абсолютная величина отклонения руля не превышает δ_max.

Если заданы абсолютная величина путевой скорости U и ограничение на угол перекладки руля δ_max, то минимальный радиус кривизны R_m допустимой траектории должен быть не меньше некоторой величины, определяемой дифференциальным уравнением модели продольного движения судна. Допустимые траектории перехода на новый курс можно искать среди ЭПО, которые строятся с помощью решения следующей экстремальной задачи. Найти такие d₀ и d₁, которые обеспечивают минимум максимальной кривизны траектории перехода на новый курс α₁ при заданных r₀, r₁, α₀, α₁, с₀=0 и с₁=0 [2]. Элементарные полиномиальные отрезки, полученные в результате решения этой экстремальной задачи, назовем оптимальными ЭПО (ОЭПО). Чтобы условия экстремальной задача были полностью определены, необходимо задать расположение точки r₁. Примем условие, что ОЭПО должна иметь осевую симметрию. Для обеспечения осевой симметрии ОЭПО [2] точку r₁ будем располагать на луче, выходящем из точки r₀ под углом α 0 + Δ φ 2 (фиг.4). Вследствие осевой симметрии ОЭПО длины касательных в начальной и конечной точках будут равны, т.е. d_Q=d₁.

На основе результатов решения серии указанных экстремальных задач для Δϕ, лежащих в диапазоне от Δϕ_min=2° до 180°, и использования свойства подобия ЭПО были построены сервисные функции r_sc(Δϕ), ƒ_Cl(Δϕ), d₁(Δϕ), ƒ_Cl_inv_{_}(Δϕ) h_c(λ_c) и h_b(λ_b).

Сервисные функции определены для ОЭПО с R_m=1. Сервисные функции описаны ниже.

ОЭПО, который обеспечивает изменение путевого угла на угол (Δϕ), и при управлении движением судна по этой траектории абсолютная величина сигнала управления не будет превышать δ_max, будем называть допустимым ОЭПО (ДОЭПО).

С элементарным полиномиальным отрезком можно связать понятие задающей окружности. Задающая окружность - это окружность, которая проходит через граничные точки r₀ и r₁ элементарного полиномиального отрезка r₀Ar₁ и является касательной к элементарному полиномиальному отрезку в этих точках (фиг.5).

Радиус задающей окружности R_sc вычисляется по формуле

R s c = R m r s c ( Δ φ ) ,                                                 (1 .2 .3)

где R_m - минимальный радиус кривизны ОЭПО, который обеспечивает изменение курса на угол Δϕ,

Δϕ - приращение путевого угла,

r_sc(Δϕ) - сервисная функция, график которой приведен на фиг.6. На фиг.6 показан график сервисной функции r_sc(Δϕ).

Согласно фиг.7 координаты точки r₁ могут быть вычислены с помощью следующего векторного выражения

r 1 = r 0 + 2 R s c sin ( Δ φ ) ( R ( Δ φ / 2 ) v 0 | v 0 | ) ,                                (1 .3 .1)

где r_0,,r₁ - координаты начальной и конечной точек траектории перехода на новый курс, соответственно,

R_sc - радиус задающей окружности,

Δϕ - приращение путевого угла,

R(Δϕ/2) - матрица поворота двумерного вектора на угол,

v₀ - вектор скорости судна в начале траектории перехода на новый курс.

На основании свойства подобия ЭПО длина d касательных в граничных точках ОЭПО вычисляются по следующей формуле

d = R m d 1 ( Δ φ ) ,                            (1 .2 .3)

где R_m - минимальный радиус кривизны ОЭПО, который обеспечивает изменение путевого угла на Δϕ,

Δϕ - приращение путевого угла,

d₁(Δϕ) - сервисная функция для вычисления длины касательных в граничных точках ОЭПО. График сервисной функции d₁(Δϕ) показан на фиг.8.

ОЭПО однозначно определяется набором параметров граничных точек {r₀,α₀,d,0,r₁,α₁,d,0},

где r_0,,r_{1 -} координаты начальной и конечной точек ЭПО, соответственно,

α_0,,α₁ - направления касательных в начальной и конечной точках ЭПО, соответственно,

d - длины касательных в начальной и конечной точках ЭПО, соответственно.

Для использования ОЭПО в алгоритмах управления необходимо вычислять координаты точек ОЭПО, координаты касательных векторов и кривизну для любого u∈ [0,1]. Поэтому набор параметров в граничных точках необходимо преобразовать в двумерные коэффициенты полинома Р₅(u) {А₀,А₁,А₂,А₃,А₄,А₅}.

Преобразование выполняется по следующим формулам.

A₀=r₀, A₁= 1 5 ·d·(sin(α₀), cos(α₀))^T

А₂=2-А₁+А₀

А₃=r₁, А₄= 1 5 ·(sin(α₁), cos(α₁))^T

А₅=2*А₄+А₃ (1.4.1)

где A₁ - двумерные коэффициенты полинома Р₅(u) (i=0…5),

r₀, r₁ - координаты начальной и конечной точек траектории перехода на новый курс, соответственно,

α₀, α₁. путевые углы в начальной и конечной точках траектории перехода на новый курс, соответственно,

d - длина касательных в начальной и конечной точках траектории перехода на новый курс.

При построении ДОЭПО необходимо учитывать, что в процессе управления движением судна по криволинейной траектории максимальные по абсолютной величине сигналы управления могут быть или во внутренних, или в граничных точках этой траектории.

Во внутренних точках ОЭПО, в которых угловая скорость судна максимальна по абсолютной величине, ω . =0. Из уравнения 0=F(b_max, ω_max) можно найти ω_max.

С помощью следующей формулы можно найти минимальный радиус кривизны R_m__c ОЭПО, обусловленный δmax во внутренних точках ОЭПО.

R m _ c = U ω max                  (1 .5 .1)

где U - абсолютная величина путевой скорости судна,

ω_max - максимальная по абсолютной величине угловая скорость судна, обусловленная δ_max.

В граничных точках ОЭПО, т.к. с₀=с₁=0, то угловые скорости тоже равны нулю ω₀=ω₁=0. Из соотношения ω ˙ _max=F(δ_max,0) можно найти ω . _max. Минимальный радиус кривизны ОЭПО R_m__b, обусловленный максимальным углом перекладки руля в граничных точках, вычисляется по следующей формуле

R m _ b = U ω ˙ max f cl    , ( Δ φ )              (1 .5 .2)

где R_m__b - минимальный радиус кривизны ОЭПО, который определяется максимальным углом перекладки руля в граничных точках ОЭПО,

Δϕ - приращение путевого угла,

ƒ_cl(Δϕ) - сервисная функция с областью значений [18,48, 0,985] и областью определения [2°, 180°], график которой приведен на фиг.9,

U - абсолютная величина путевой скорости судна,

ω ˙ _max - абсолютная величина производной угловой скорости судна в горизонтальной плоскости в граничных точках, обусловленная δ_max.

Допустимой траекторией, обеспечивающей изменение путевого угла на Δϕ, будет ОЭПО с минимальным радиусом кривизны R_m, равным

R m = max ( R m _ c , R m _ b ) ,                                           (1 .5 .3)

где R_m__с - минимальный радиус кривизны ОЭПО, который определяется максимальным углом перекладки руля во внутренних точках ОЭПО,

R_m__b - минимальный радиус кривизны ОЭПО, который определяется

максимальным углом перекладки руля в граничных точках ОЭПО.

Пусть известна высота Н₁ криволинейного отрезка (см. фиг.2 и 3). Из элементарной геометрии следует, что

H 1 = s i g n ( H ) ⋅ R s c ⋅ ( 1 − cos ( Δ φ ) )                                           (1 .6 .1)

где Н - расстояние смещения параллельного курса от текущего курса,

sign(x) - функция, равная: 1 при х>0, -1 при х<0, 0 при х=0,

H₁ - высота криволинейного отрезка (см. фиг.2 и 3),

R_sc - минимальный радиус кривизны ОЭПО, который обеспечивает изменение курса на угол Δϕ,

Δϕ - приращение путевого угла.

Рассмотрим уравнение, полученное подстановкой (1.5.1) в (1.6.1)

H 1 = s i g n ( H ) U ω max r s c ( Δ φ ) ( 1 − cos , ( Δ φ ) )                                           (1 .6 .2)

где H₁ - высота криволинейного отрезка (фиг.2 и 3),

Н - расстояние смещения параллельного курса от текущего курса,

U - абсолютная величина путевой скорости судна,

ω_max - максимальная по абсолютной величине угловая скорость судна, обусловленная δ_max,

r_sc(Δϕ) - сервисная функция, график которой приведен на фиг.6,

Δϕ - приращение путевого угла. Рассмотрим уравнение, полученное подстановкой (1.5.2) в (1.6.1)

H 1 = s i g n ( H ) U ω ˙ max f c l ( Δ φ ) r s c ( Δ φ ) ( 1 − cos , ( Δ φ ) )                                           (1 .6 .3)

где Н₁ - высота криволинейного отрезка (см. фиг.2 и 3),

Н - расстояние смещения параллельного курса от текущего курса,

U - абсолютная величина путевой скорости судна,

ω ˙ _max - абсолютная величина производной угловой скорости судна в горизонтальной плоскости в граничных точках, обусловленная δ_max,

ƒ_cl(Δϕ) - сервисная функция, график которой приведен на фиг.9,

r_sc(Δϕ) - сервисная функция, график которой приведен на фиг.6,

Δϕ - приращение путевого угла.

Выражения (1.6.2) и (1.6.3) рассмотрим как уравнения для Δϕ. Согласно разделу 5, необходимо выбрать для нахождения Δϕ то уравнение, которому соответствует наибольший из двух радиусов R_m__c и R_m__b. Если Δϕ найден, то, используя выражения (1.5.1), (1.5.2), (1.3.1), (1.3.2), можно будет рассчитать наборы параметров граничных точек двух ДОЭПО, входящих в траекторию перехода на параллельный курс.

Выделим из (1.6.2) и (1.6.3) функции h_c__inv(Δϕ) и h_b__inv(Δϕ), соответственно

h_c__inv(Δϕ)=r_sc(Δϕ)(1-cos(Δϕ))

h_b__inv(Δϕ)=ƒ_cl(Δϕ)r_sc(Δϕ)(1-cos(Δϕ)),

где r_sc(Δϕ) - сервисная функция, график которой приведен на фиг.6,

ƒ_cl(Δϕ) - сервисная функция, график которой приведен на фиг.9,

Δϕ - приращение путевого угла.

На основе функции h_c__inv(Δϕ) построена обратная к ней сервисная функция h_c(λ_c) с областью значений [2°, 150°] и областью определения [0,00072, 2,223] (фиг.10). На основе функции h_b__inv(Δϕ) построена обратная к ней сервисная функция h_b(λ_b) с областью значений [2°, 130°] и областью определения [0,01325, 3,549] (фиг.11).

Из (1.6.2) следует, что при λ c = | H 1 | ω max U и λ_c∈[0,00072, 2,223] угол изменения курса Δϕ_c, обусловленный δ_max во внутренних точках ОЭПО, с учетом правила знаков для H и Δϕ равен

Δ φ c = s i g n ( H ) ⋅ h с ( λ c )                   (1 .6 .4)

где Н₁ - высота криволинейного отрезка (фиг.2 и 3),

Н - расстояние смещения параллельного курса от текущего курса,

h_c(λ_c) - сервисная функция, график которой приведен на фиг.10.

Аналогично, из (1.6.3) следует, что при λ b = | H 1 | ω ˙ max U и λ_b∈[0,01325, 3,549] угол изменения курса Δϕ_b, обусловленный максимальным углом перекладки руля в граничных точках, равен

Δ φ b = s i g n ( H ) ⋅ h b ( λ b )                   (1 .6 .5)

где Н₁ - высота криволинейного отрезка (фиг.2 и 3),

Н - расстояние смещения параллельного курса от текущего курса,

h_c(λ_c) - сервисная функция, график которой приведен на фиг.11.

Рассмотрим диапазон возможных значений абсолютной величины приращения путевого угла Δϕ_min≤|Δϕ|≤Δϕ_max. Для обеспечения совместимости областей значений функций h_c(λ_c) и h_b(λ_b) должны выполняться следующие условия: Δϕ_min≥2° и Δϕ_max≥130°.

Когда заданы Δϕ_min, Δϕ_max, то можно вычислить соответствующие им высоты H₁__min и H₁__max ДОЭПО. При вычислении указанных высот необходимо учитывать следующие разности минимальных радиусов кривизны

Δ R m _ min = R m _ c − R m _ b       для   Δ ϕ min Δ R m _ max = R m _ c − R m _ b       для   Δ ϕ max                                         (1 .6 .6)

где для вычисления R_m__с используется правая часть выражения (1.5.1), для вычисления R_m__b используется правая часть выражения (1.5.2).

Если выполнено условие a) ΔR_m__min≥0, то

H 1 _ min = s i g n ( H ) U ω max r s c ( Δ ϕ ) ( 1 − cos ( Δ ϕ min ) )                                           (1 .6 .7)

иначе

H 1 _ min = s i g n ( H ) U ω ˙ max f c l ( Δ ϕ ) r s c ( Δ ϕ ) ( 1 − cos ( Δ ϕ min ) )                                           (1 .6 .8)

где H_{1_min} - абсолютная величина высоты ДОЭПО, когда приращение путевого угла равно Δϕ_min,

Н - расстояние смещения параллельного курса от текущего курса,

U - абсолютная величина путевой скорости судна,

ω_max - максимальная по абсолютной величине угловая скорость судна, обусловленная δ_max