Способ снятия неоднозначности измерения дальности и скорости для импульсно-доплеровских систем

Способ снятия неоднозначности измерения дальности и скорости для импульсно-доплеровских систем

Иллюстрации

Показать все

Реферат

Изобретение относится к дистанционному зондированию пространства с целью определения дальности и скорости рассеивателей, в частности к решению вопроса неоднозначности измеряемых скоростей и дальностей при использовании когерентных импульсных (доплеровских) систем, например, для снятия неоднозначности измерения скоростей рассеивателей в метеорологических доплеровских РЛС на больших дальностях.

Традиционные импульсно когерентные (доплеровские) системы (ИКС), использующие фиксированную частоту повторения импульсов F_повт, имеют ограничения на однозначно измеряемую дальность R_мax и однозначно измеряемую скорость V_мax. Измерения однозначны, если дальность рассеивателей не превышает R_маx=С/2 F_повт, а максимальная проекция скорости рассеивателей не превышает V_мax=λF_повт/4. Здесь С - скорость света в вакууме, λ - длина волны зондирующего излучения. В результате справедливо соотношение: R_мaxV_мax≤Сλ/8.

Известен корреляционный метод однозначного измерения дальности и скорости, основанный на измерении в импульсном некогерентном режиме профиля интенсивности обратно рассеянного сигнала вдоль всей трассы распространения излучения, и измерения суммарного доплеровского спектра вдоль всей трассы с помощью непрерывной доплеровской системы. С периодичностью смены рассеивателей в луче цикл измерений повторяют, а скорость на каждой дальности определяют по доплеровской частоте, на которой получается максимум функции взаимной корреляции между профилем интенсивности обратно рассеянного сигнала (отражаемостью) и спектральной плотностью доплеровского спектра [1].

Наиболее близким является метод расширения диапазона однозначности измеряемых скоростей и дальностей за счет изменения частоты повторения импульсов [2]. При этом удается расширить диапазон измеряемых величин примерно в 2-3 раза. Недостаток данного метода заключается в том, что при попытке большего расширения диапазона скоростей вновь возникает неоднозначность. Кроме того, при множественных целях или множественных рассеивателях возникает широкий спектр, при котором применение метода осложняется или становится невозможным.

Технический результат предложенного способа заключается в снятии неоднозначности при измерении дальности и скорости за счет того, что измерения проводят при двух частотах повторения импульсов. При низкой частоте повторения, которая обеспечивает однозначное определение дальности, измеряют доплеровские спектры обратно рассеянного сигнала вдоль всей трассы распространения, в частности мощность и ширину спектра доплеровского сигнала на всех дальностях по трассе. Затем, при высокой частоте повторения импульсов, которая обеспечивает однозначность измеряемых скоростей рассеивателей, измеряют суммарные доплеровские спектры обратно рассеянных сигналов, полученных одновременно с нескольких дальностей, а по корреляции между параметрами доплеровских спектров вдоль трассы и суммарными доплеровскими спектрами определяют проекции скоростей рассеивателей на всех дальностях. Для повышения надежности результатов в сложных случаях, например при множественных целях на всех дальностях, измерения повторяют с периодичностью смены рассеивателей в зондируемом объеме или с периодичностью изменения отражаемости рассеивателей в зондируемом объеме, а корреляционные характеристики накапливают.

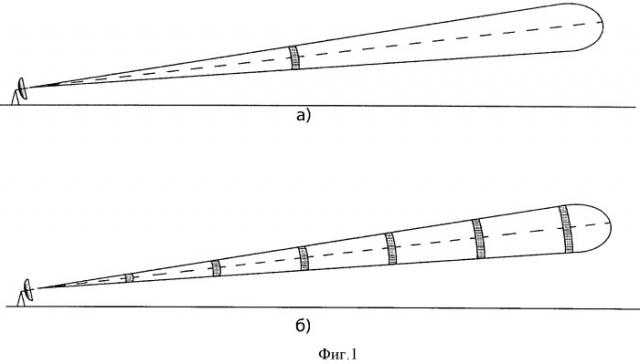
На фигуре 1, а представлена геометрия зондирования и формирование сигнала при низкой частоте повторения импульсов, при котором однозначно определяется дальность рассеивателей, и определяются доплеровские спектры S(v, R) на всех дальностях R. На фигуре 1, б показан высокочастотный режим повторения импульсов, который обеспечивает однозначность измеряемых проекций скоростей рассеивателей. В этом режиме без искажений определяются суммарные доплеровские спектры обратно рассеянных сигналов, полученных одновременно с нескольких дальностей, равноотстоящих друг от друга на расстоянии ΔR=R_i+1-R₁=С/2F_повт.2.

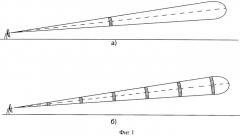
На фигуре 2 представлен пример доплеровских спектров S(v, R₁), S(v, R₂), …, S(v, R_n), полученных при низкой частоте повторения импульсов F_повт, которая обеспечивает однозначное определение дальности вдоль трассы, но при которой искажаются спектры за счет «сгибания» и наложения участков спектра при низкой частоте повторения. В качестве обобщенной доплеровской частоты в спектрах мы будем использовать проекцию скорости рассеивателей v, которая связана с доплеровским сдвигом F_допл соотношением: v=λF_допл/2. Значения дальностей R₁, R₂, …, R_n соответствуют набору равноотстоящих дальностей, для которых регистрируется суммарный доплеровский спектр, полученный при высокой частоте повторения импульсов F_повт.2. На чертеже общее число дальностей n=6, однако спектры на дальностях R₃, R₄ не показаны исходя из предположения малого уровня сигнала (отсутствия в рассматриваемом примере отражателей на этих дальностях). Спектр S(v, R₆), показанный на фиг.2, г, имеет максимум на краю из-за «сгибания» и наложения участков спектра при низкой частоте повторения импульсов.

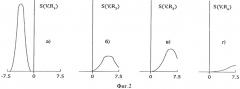
На фигуре 3 изображен доплеровский спектр S₀(v), из рассмотренного примера, полученный при высокой частоте повторения импульсов F_повт.2, которая обеспечивает неискаженную форму спектра во всем диапазоне измеряемых скоростей. Этот спектр равен сумме неискаженных спектров, полученных от набора дальностей R₁, R₂, …R_n, равноотстоящих друг от друга на расстоянии ΔR=R_i+1-R_i=С/2F_повт2.

Рассмотрим способ на примере метеорологического доплеровского радиолокатора, дальность зондирования которого R_max составляет 250 км, длина волны λ=5 см, а диапазон возможных скоростей метеообразований составляет V_мax=±50 м/с. При заданной дальности зондирования R_max=250 км для однозначного определения дальности частота повторения импульсов F_повт.1 должна составлять F_повт.1=C/2·R_max=600 Гц. В этом случае будет обрабатываться сигнал только с одной дальности R, которая определяет временем задержки τ=2R/C, (см. фиг.1а). При этом режиме зондирования и данной частоте повторения на всех дальностях R определяют доплеровские спектры S(v, R). Однако спектры получаемых сигналов могут быть искажены из-за «сгибания» и наложения участков спектра относительно крайних частот (однозначно измеряемых скоростей) ±7,5 м/с. Такой режим измерений не обеспечивает регистрацию опасных метеорологических явлений, при которых скорость может достигать ±50 м/с. Но даже в этом случае можно определить мощность сигнала и оценить ширину спектра на всех дальностях R вдоль траектории распространения излучения.

На фиг.2 представлены примеры доплеровских спектров S(v, R₁), S(v, R₂), S(v, R₅), S(v, Rg), полученных с четырех различных дальностей при низкой частоте повторения. Значения дальностей R₁, R₂, …, R_n соответствуют набору равноотстоящих дальностей, для которых будет регистрироваться суммарный доплеровский спектр, полученный при высокой частоте повторения импульсов F_повт2. Спектры на дальностях R₃, R₄ не показаны, из предположения малого уровня сигнала (отсутствия в рассматриваемом примере отражателей, облаков или осадков, на этих дальностях). Спектр S(v, R₆) имеет максимум на краю из-за «сгибания» и наложения участков широкого спектра при низкой частоте повторения импульсов.

Второй режим измерения производится по той же трассе, что и первый, но частоту повторения импульсов выбирают из условия F_повт.2=4V_мax/λ. Если максимальная скорость в опасных метеоситуациях не превышает ±50 м/с, то частота повторения F_повт.2=4000 Гц. В этом случае на трассе длиной 250 км одновременно будет существовать несколько областей рассеивания (6 или 7, в зависимости от задержки измерений), отстоящих друг от друга на расстоянии ΔR=37,5 км, см. фиг.1, б. Рассеянный сигнал будет приниматься антенной одновременно со всех этих областей. По задержке между стробом импульса и моментом регистрации сигнала легко рассчитать все дальности R₁, R₂, …, R_n, которые формируют результирующий сигнал на приемной антенне. Суммарный доплеровский спектр S₀(v) при частоте повторения F_повт.2 вычисляется без искажений и представляет собой сумму истинных неискаженных спектров сигналов со всех 6 или 7 вычисленных дальностей, фиг.3. Как правило, этот спектр будет изрезанным, с набором локальных экстремумов. Задача корреляционной обработки заключается в том, чтобы указать истинное расположение спектров с каждой дальности на общем спектре. Это будет означать определение истинных проекций скорости рассеивателей на каждой дальности.

Пример корреляционной обработки по мощности сигналов заключается в том, чтобы на наборе спектров, представленных на фиг.2, выбрать самый мощный сигнал (в примере он соответствует первой дальности S(v, R₁)), затем в суммарном неискаженном спектре S₀(v) найти аналогичный по мощности выброс спектральной плотности. Его положение в спектре S₀(v) центрировано на частоте v₀₁=-3.5 м/с, что дает неискаженное значение проекции скорости рассеивателей на дальности R₁. На следующем шаге из спектра S₀(v) вычитается спектр S(v, R₁), максимум которого сдвинут в положение v₀₁. В результате получаем спектр, который сформирован оставшимися дальностями. Процедура повторяется для следующего по мощности сигнала до тех пор, пока все дальности не будут привязаны по истинной частоте.

Примером корреляционной обработки с учетом интенсивности и ширины спектров S(v, R₁) может служить формирование невязки H(v₀) между S(v, R₁) и общим спектром S₀(v) и нахождение минимума невязки по вектору обобщенных доплеровских частот (равных проекции скоростей рассеивателей на направление зондирования на всех n дальностях) v₀={v₀₁, v₀₂, …, v_0n}:

H ( v 0 ) = ∫ ν [ S 0 ( ν ) − ∑ i = 1 n S ( ν − ν 0 i , R i ) ] 2 d ν                         ( 1 )

В результате процедуры минимизации невязки получаем вектор частот v₀, который указывает проекции скоростей рассеивателей на всех дальностях. Данная процедура корреляционной обработки в нашем примере дала следующий вектор проекций скоростей v₀={-3.5, 5.0, -, -, 20.0, 24.5}, который соответствует всем 6 дальностям (четвертая и пятая дальности отсутствуют из-за малости сигнала). Это процедура уже учитывает не только мощность, но и ширину каждого спектра S(v, R_i).

В случае, если спектры S(v, R_i) центрированы на близких доплеровских частотах и сравнимы по мощности (близки первые и вторые моменты доплеровских спектров), одного цикла измерений может быть недостаточно для точной привязки всех дальностей по скоростям. В этом случае цикл измерений повторяют с периодичностью смены рассеивателей в луче или с периодичностью изменения отражаемости рассеивателей в зондируемом объеме и проводят корреляционное накопление невязки по всем j=1, 2, …, m циклам измерений:

H ( v 0 ) = ∑ j = 1 m { ∫ ν [ S 0 ( j ) ( ν ) − ∑ i = 1 n S ( j ) ( ν − ν 0 i , R i ) ] 2 d ν }                         ( 2 )

где верхний индекс j у спектров соответствует номеру цикла. В результате нахождения минимума невязки по вектору v₀={v₀₁, v₀₂, …, v_0n} получают истинные проекции скоростей, которые соответствуют заданному набору дальностей R₁, R₂, …, R_n.

Корреляционное сравнение спектров S(v, R_i) на наборе дальностей и общего спектра S₀(v) может проводиться не только по мощности и ширине спектров, но и по всем другим характеристикам сравниваемых сигналов: поляризации, деполяризации, спектрам флуктуации интенсивности, тонкой структуре спектров. Введение дополнительных параметров корреляции повышает устойчивость привязки скорости к каждой дальности и зависит от специфики конкретной задачи радиолокационного обнаружения.

Достоинством предложенного способа является отсутствие принципиальных ограничений на дальность рассеивателей и их скорость. Кроме того, возможно использование любых длин волн, в том числе более коротких, чем это принято в настоящее время. Это позволяет уменьшить размеры и массу антенных систем и всей аппаратуры в целом, создавать компактные системы с расширенными измерительными возможностями.

Литература

1. Стерлядкин В.В. Корреляционно доплеровская реконструкция поля скоростей. Известия АН СССР, сер. Физика атмосферы и океана. Т.30, №5, 1994, с.623-629.

2. Белый Ю.И., Мареев А.Ю. Способ измерения дальности и скорости импульсно-доплеровской радиолокационной станцией. Патент РФ, RU №2206102 С1, 10.06.2003. Бюл. №16.

1. Способ снятия неоднозначности измерения дальности и скорости для импульсно-доплеровских систем, заключающийся в получении доплеровских спектров обратно рассеянных сигналов при различных частотах повторения зондирующих импульсов,отличающийся тем, что при низкой частоте повторения импульсов, которая обеспечивает однозначное определение дальности, измеряют доплеровские спектры обратно рассеянного сигнала вдоль всей трассы распространения, затем при высокой частоте повторения, которая обеспечивает однозначность измеряемых скоростей рассеивателей, измеряют суммарные доплеровские спектры обратно рассеянных сигналов, полученных одновременно с нескольких дальностей, а по корреляции между параметрами доплеровских спектров вдоль трассы и суммарными доплеровскими спектрами определяют проекции скоростей рассеивателей на всех дальностях.

2. Способ по п.1, отличающийся тем, что цикл измерений повторяют с периодичностью смены рассеивателей или с периодичностью изменения отражаемости рассеивателей в зондируемом объеме, а корреляционные характеристики накапливают.